I.3.1 Doppelspalt-Versuch klassisch
(mit Wasserwellen, Schall oder Licht)
Beobachtungen und ihre Deutung:
- Minima/Maxima in der Interferenzfigur; dazwischen glatte Übergänge
- Interferenz / Überlagerung der Wellen / "neue Mathematik: 1+1 = 4 bzw. 1+1 = 0"
- Interferenzbedingung
- Auswertungsmethoden
- Schall "ist" eine Wellenerscheinung
- "Ist" auch Licht eine Wellenerscheinung?
- Kohärenzbedingungen: Kohärenz-, Koinzidenz- und Sichtbarkeitsbedingung
I.3.2 Doppelspalt-Versuch
mit Licht und mit Elektronen-, Neutronen-, Atom-Strahlen, ...
(1) Grundexperiment
(1) Grundexperiment:
- Schilderung des Experiments mit Elektronen von Jönsson (1961); analoge Erscheinung bei beliebigen Teilchen
- deBroglie stellte spekulativ 1923/24 die Hypothese
auf:
Einem Strahl beliebiger identischer Teilchen, die alle den gleichen Impuls p mit dem Betrag p haben, lässt sich eine Welle zuordnen und es gilt:
p = h/λ (E = h·f )
Damit konnte man hoffen, auch mit Elektronen, Atomen, Molekülen, Neutronen, ... Interferenz zu erhalten, z.B. am Doppelspalt mit der gleichen Interferenzbedingung wie bei der Interferenz von klassischen Wellen. Die Art dieser Zuordnung blieb zunächst noch ungeklärt.
- Die Beobachtungen lassen sich für beliebige
Teilchenstrahlen (Neutronen-, Atom-,
Molekül-Strahlen, ...)
verallgemeinern.
- Maxima und Minima entstehen bei gleichen Interferenzbedingungen wie bei der Interferenz von Wellen
Hinweis: Historisch wurden Interferenzen bei Materiestrahlung erstmals bestätigt mit Kristallgitter-Interferenzen von Elektronen (Davisson und Germer 1923-1927 bzw. G.P. Thomson; Deutung durch Elsässer 1925), später auch von Neutronen (von Halban und Preiswerk 1936, nach der Entdeckung des Neutrons 1934). Verbesserte Experimente mit Neutronen werden durchgeführt, seitdem man mit Kernreaktoren starke Neutronenquellen zur Verfügung hat. Hier sei auf die Neutroneninterferometer-Versuche der Wiener Gruppe um Rauch und Zeilinger hingewiesen. Interferenzen bei Wasserstoff-Molekülen und Helium-Atomen wurden erstmals 1929 von O. Stern und Estermann in Hamburg beobachtet. Neuere Experimente stammen z.B. von Pfau u.a. oder von Dürr u.a. mit Atomstrahlen oder von Zeilinger u.a. mit Fulleren-Molekülen oder Molekülen mit noch größeren Massen.
Hinweis auf ein verwandtes Experiment mit Elektronen von Möllenstedt, das dem optischen Biprisma-Versuch entspricht.
|
mit einzelnen Photonen, Elektronen, Atomen, Molekülen ... : Einteilchen-Interferenz
(2) Doppelspalt-Versuch bei reduzierter Leistung der Quelle
. . . . . . . . .
. . . . . . .
|
|
mit einzelnen Photonen, Elektronen, Atomen, Molekülen ... : Einteilchen-Interferenz
. . . . . . . . .
. . . . . . . . .
|
|
mit einzelnen Photonen, Elektronen, Atomen, Molekülen ... : Einteilchen-Interferenz
. .
. . . . . . . . .
. . . . . . .
|
|
mit einzelnen Photonen, Elektronen, Atomen, Molekülen ... : Einteilchen-Interferenz
. .
. . . . . . . . .
. . .
|
|
mit einzelnen Photonen, Elektronen, Atomen, Molekülen ... : Einteilchen-Interferenz
.
. . . . . . . . .
. . . . . |
(2) Doppelspalt-Versuch bei reduzierter Leistung der Quelle (Versuch von Taylor 1909 u.a.):
Zur genaueren Untersuchung reduziert man bei einem klassischen Doppelspalt-Versuch die Intensität der Strahlung immer stärker. (Um das zu erproben, können Sie sich ein Simulationsprogramm von Muthsam aus dem Internet herunterladen.) Außer Schwierigkeiten mit der Nachweisgenauigkeit sollte man doch wohl nichts anderes erwarten als üblich? Man erwartet, dass die Interferenzfigur immer "schwächer" wird, aber abgesehen davon doch eine unveränderte Verteilung zeigt mit allmählichen Übergängen zwischen Maxima und Minima. Oder etwa doch nicht? Wenn man die Intensität schließlich soweit reduziert hat, dass immer nur ein Teilchen **) in der Apparatur ist, sollte sich dieses dann auf die vielen Maxima sozusagen "aufteilen"?
Aber Sie wissen doch schon von Kap. I.2.2: Teilchen treten immer als ganze Teilchen auf, Elektronen immer als ungeteilte Elektronen, Photonen immer als ungeteilte Photonen.
Wie lässt sich dieser scheinbare Widerspruch lösen?
Zum Nachweis der Teilchen auf dem Schirm wird ein
Flächenzähler verwendet. Im Falle von Licht könnte das ein im
Rechteck angeordnetes Feld von Fotozellen sein. Sobald eine der
Fotozellen ein Teilchen nachweist, wird ein Signal an einen
elektronischen Zähler geschickt, der - abhängig vom jeweiligen
Ort der Fotozelle mit den (mittleren) Koordinaten x und y - die
dort nachgewiesenen Teilchen zählt. In den folgenden
schematischen Zeichnungen wird das Ansprechen eines Zählers
durch Einfärben ihrer empfindlichen Fläche markiert. Es wird
schematisch gezeigt, wie sich das Schirmbild nach und nach
entwickelt, wenn die Intensität so gering ist, dass sich immer
nur ein Teilchen in der Apparatur befindet.
|
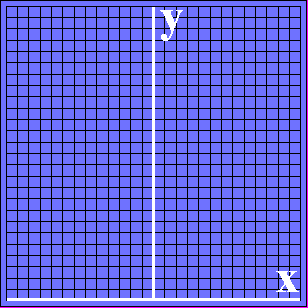
Schirmbild bei der Doppelspalt-Interferenz mit wachsender Zahl von Teilchen, wenn ein Flächenzähler verwendet wird, der die Tatsache des Ansprechens des Zählers und seinen Ort (x,y) registriert (schematisch): |
|
 (1a) (1a) |
 (1b) (1b) |
| (1a) Jedes der Felder stellt schematisch einen
flächenhaften Zähler auf dem Schirm dar. Aufgetragen
sind hier die beiden Koordinatenachsen auf dem Schirm.
Sobald einer der Zähler ein Teilchen nachweist, wird
seine Fläche eingefärbt, zunächst purpurfarben, beim
zweiten Teilchen gelb usw.
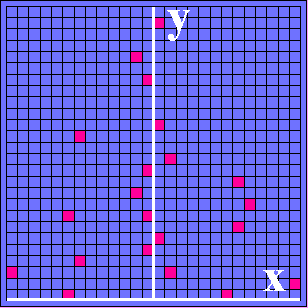
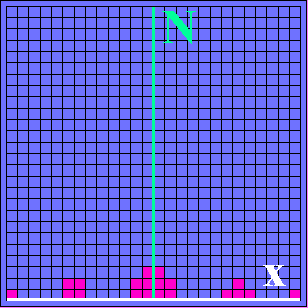
(1b) Ganz zufällig sprechen einzelne Zähler an. (1c) Die Zählergebnisse des Flächenzählers sind so nach unten "zusammengeschoben", dass das Zählen erleichtert und die Verteilung besser erkennbar wird. Nach rechts ist wieder die x-Koordinate auf dem Schirm dargestellt, nach oben die Anzahl N der bei der jeweiligen x-Position ansprechenden Zähler. Trotz der zufälligen Verteilung der nachgewiesenen Teilchen wird bereits eine Struktur erkennbar: die relativ meisten Teilchen werden in der Nähe ganz bestimmter Stellen nachgewiesen. |
 (1c) (1c) |
 (2a) (2a) |
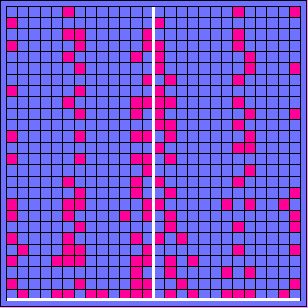 (3a) (3a) |
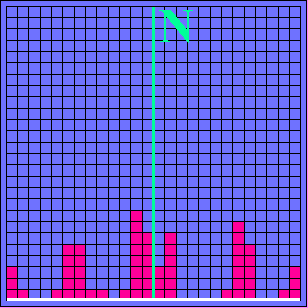 (2b) (2b) |
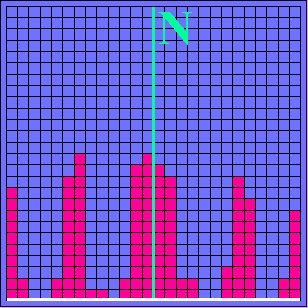 (3b) (3b) |
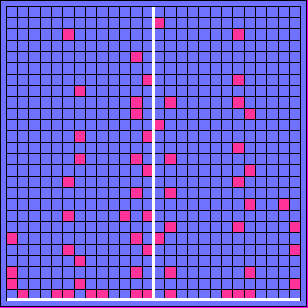
| (2a), (2b): Zufällig verteilte einzelne Zähler sprechen an. | (3a),(3b) Mit zunehmender Teilchenzahl bildet sich eine immer deutlicher strukturierte Verteilung der registrierten Teilchen heraus. |
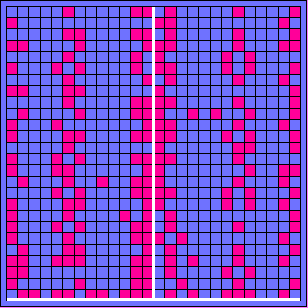 (4a) (4a) |
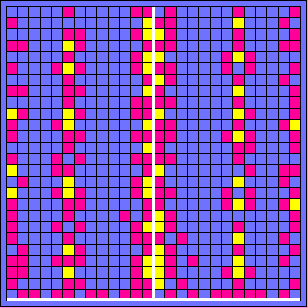 (5a) (5a) |
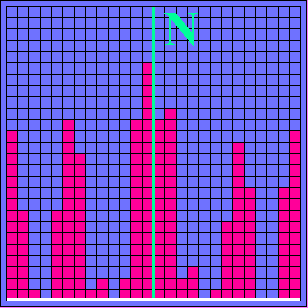 (4b) (4b) |
 (5b) (5b) |
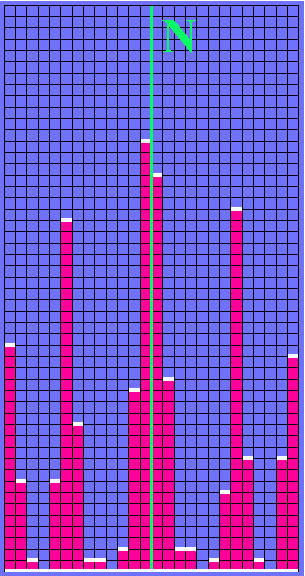
| (5b) Mit zunehmender Teilchenzahl wird die
Verteilung immer symmetrischer und "glatter". Wenn die
Teilchenzahl gegen unendlich geht, geht die weiße Kurve
in die Interferenzfigur von klassischen Wellen über. Man
erkennt hier schon die ungefähre Lage der Minima und
Maxima.
Beachten Sie: In dieser Zeichnung ist der Maßstab in der Vertikalen geändert! Die gelben Felder in der Zeichnung darüber sind Felder, in denen 2 Teilchen registriert wurden. |
|
Aus den Beobachtungen schließt man:
- Die Teilchen werden immer als Ganze an zufällig verteilten Orten auf dem Schirm nachgewiesen, die Nachweisorte sind statistisch verteilt. Ein Nachweisort für ein bestimmtes Teilchen ist nicht vorhersagbar.
- Aber die Interferenzfigur ist nicht bedeutungslos: Die Verteilung der registrierten Teilchen weist starke Ähnlichkeit mit der Interferenzfigur auf. Dort, wo das Amplitudenquadrat der Welle maximal ist, findet man die meisten Teilchen, nahe der Minima, also dort, wo das Amplitudenquadrat der Welle 0 ist, findet man fast keine Teilchen.
- Die relative Häufigkeit, ein Teilchen (Photon, Elektron oder Atom, ...) in der Umgebung einer Stelle nachzuweisen, verhält sich ähnlich wie das Amplitudenquadrat der Welle. Im Unterschied dazu ist die Häufigkeitsverteilung im Experiment unregelmäßig, gestuft. Mit zunehmender Teilchenzahl nähert sich die unregelmäßig gestufte Häufigkeitsverteilung immer mehr dem glatten Verlauf des Amplitudenquadrats der Welle.
- Andererseits nähert sich die beobachtete Häufigkeitsverteilung nach dem empirischen "Gesetz der großen Zahlen" mit zunehmender Teilchenzahl immer mehr der Wahrscheinlichkeitsverteilung für den Nachweis eines Teilchens in der Umgebung einer Stelle. (Die Wahrscheinlichkeit, ein Teilchen genau an einem Ort nachzuweisen, ist immer 0, da ein Punkt ja keine Ausdehnung hat.*))
- Wieder beobachten Sie einen Doppelaspekt: Einerseits wird der Nachweis eines Teilchens durch den objektiven Zufall gesteuert, andererseits ergibt sich aus dem Vergleich der Häufigkeitsverteilung bzw. der Wahrscheinlichkeitsverteilung mit dem Amplitudenquadrat der Welle eine gesetzmäßige Aussage.
*) Dies ist der Grund, weshalb wir statt vom Nachweis an einer Stelle immer vom Nachweis in der Umgebung einer Stelle sprechen. Im eindimensionalen Fall könnte das ein Intervall der Breite Δx um eine Stelle mit der Koordinate x sein, im dreidimensionalen Fall ist das ein Volumenelement ΔV um eine Stelle mit dem Ortsvektor r.
Ein einzelnes Teilchen kann überall nachgewiesen werden, allerdings mit unterschiedlicher Wahrscheinlichkeit. Diese ist besonders klein in der Nähe der Nullstellen der Wahrscheinlichkeitsdichte, besonders groß in der Nähe der Maxima. Aus dem Nachweis eines einzelnen Photons oder Elektrons oder Atoms kann man bzgl. der Interferenzfigur überhaupt nichts aussagen. Beobachtet man aber sehr viele Teilchen, und trägt ihre Nachweisorte in ein x-N-Diagramm ein (x: Ort längs des Schirms, N: Anzahl der in der Umgebung eines solchen Ortes gezählten Teilchen), so entsteht eine Graph vom Verlauf einer Interferenzfigur.
Oder: Wiederholt man den Versuch mit einem einzigen Teilchen, das vor dem Versuch immer wieder mit gleichen Eigenschaften ausgestattet wird, man sagt "gleich präpariert" wird, und trägt die einzelnen Nachweisorte in eine Graphik wie oben ein, so entsteht genauso wieder eine identische Interferenzfigur. Man schließt:
|
Sogar einzelne ununterscheidbare
Teilchen sind interferenzfähig!
(Einteilchen-Interferenz) |
Einteilchen-Interferenz wird allerdings erst sichtbar, wenn der Interferenz-Versuch sehr häufig mit einzelnen Teilchen oder gleich mit sehr vielen Teilchen wiederholt wird.
Ein analoger Versuch mit der Interferenz einzelner Fulleren-Moleküle zeigt die gleichen Erscheinungen. Bei vielen gleichartigen Versuchen ergibt sich eine Interferenzfigur.
(3) Interferenz scheint auf Wellen hinzuweisen. Aber
schon 1926, als die Quantentheorie im Entstehen war und
Interferenzversuche mit Licht und Elektronen bekannt waren,
hatte Max Born eine Wahrscheinlichkeitsdeutung für
die anscheinend beteiligten "Wellen" gegeben:
| Born'sche Wahrscheinlichkeitsdeutung (1926):
Die "Welle" zur Beschreibung eines Quantensystems ist keine realistische Welle. Sie hat selbst keine reale Bedeutung. Aber das Betragsquadrat der "Welle" ist proportional zur Wahrscheinlichkeit, ein Teilchen in einem Raumelement um einen Punkt herum nachzuweisen (in einer Umgebung eines Punktes). Die Wahrscheinlichkeit ist auch noch proportional zum Volumen ΔV dieses Raumelements. |
Die Proportionalität zum Volumen ΔV ist auch plausibel, weil es umso wahrscheinlicher ist, darin ein Teilchen zu finden, je größer das Raumelement ist. Die beschriebenen Versuche mit reduzierter Intensität, die diese statistische Deutung besonders anschaulich machen, wurden von Taylor 1909 (für Photonen) durchgeführt, mit voller Präzision erst viel später durch Grangier und Aspect und durch Janossy (1957) und Tonomura (1989) (für Elektronen).
Heute wissen wir sogar noch genauer: Solche nicht realistischen Wellen dienen ausschließlich zur Berechnung von Wahrscheinlichkeiten und erfüllen weniger den dreidimensionalen Anschauungsraum als die Köpfe der Physiker, die damit umgehen und sehr erfolgreich die Natur beschreiben.
(4) Dabei kann man völlig ausschließen, dass die Entstehung der Interferenzfigur die Folge einer Wechselwirkung dieser vielen Teilchen oder eines "Zusammenwirkens" vieler Teilchen sei. Wir haben ja gesehen, dass man die Intensität so herunterregeln kann (Taylor-Versuch 1909), dass immer nur ein einziges Teilchen in der Apparatur vorhanden ist **). Und Photonen wechselwirken ohnehin kaum miteinander. Und dennoch erhält man bereits mit einzelnen Teilchen die beschriebene Interferenzfigur, wenn auch erst nach und nach bei vielen Versuchen.
(5) Der Grangier-Roger-Aspect-Versuch mit einzelnen Photonen beim Doppelspalt hat die gleiche Funktion wie die Versuche von Taylor, Janossy, Tonomura u.a. Er sichert, dass wirklich immer nur ein Photon im Experiment ist. Das Ergebnis ist wie eben beschrieben, nur viel zuverlässiger. Der G-R-A-Versuch am Strahlteiler gilt als schärfstes Indiz für die Existenz von Photonen.
(6) Experimentelle Beispiele: Elektronen, Licht, Atome, Fulleren, Neutronen, ... zeigen ähnliche Ergebnisse.
(7) Vorläufige Folgerung:
Um den Doppelspalt-Versuch qualitativ zu erklären, bietet sich in beschränktem Maße ein "Wellenbild" an. Damit kann man dann sogar die Lage der Minima und Maxima quantitativ erklären. Die dabei benutzte Welle ist aber nicht realistisch aufzufassen. Sie erhält einen nachprüfbaren Sinn erst durch die Born'sche Wahrscheinlichkeitsdeutung. Tatsächlich entsteht die Interferenzfigur erst allmählich aus lauter einzelnen Teilchen-Nachweisen. Aber die Interferenz kommt bereits bei einem einzigen Teilchen in der Apparatur zustande.
Wenn dagegen Messungen an einzelnen Teilchen gemacht werden, wie z.B. schon beim Nachweis der Teilchen, die eine Öffnung des Doppelspalts passiert haben, erscheint das "Teilchenbild" als zweckmäßiger, aber auch dieses versagt bei genauerem Hinsehen, wie wir bald erkennen werden.
**)Seit 1963 (Glauber) weiß man, dass beim Taylor-Versuch bzw. bei stark abgeschwächtem Laserlicht die Anwesenheit von genau einem Photon in der Apparatur keineswegs gesichert ist. Vgl. kohärente Zustände.
I.3.4 Deutungsversuch (1):
Sind also Elektronen oder Photonen klassische*) Wellen?
Nein, bei Reduzierung der Intensität bzw. Bestrahlungstärke beobachtet man keine kontinuierliche Veränderung der Amplituden in der Interferenzfigur, sondern eine "körnige Struktur" der Interferenzfigur: einzelne statistisch verteilte Nachweise ganzer Teilchen mit einer unregelmäßig gestuften Häufigkeitsverteilung. Im Extremfall bei einem Teilchen findet nur ein einziger Teilchen-Nachweis an einer irgendeiner Stelle innerhalb der Interferenzfigur statt. Mit zunehmender Teilchenzahl findet man immer mehr Teilchen in der Nähe der Maxima der Interferenzfigur, kaum welche in der Nähe der Minima der Interferenzfigur. Wellen haben nur im Zusammenhang mit der Wahrscheinlichkeitsdeutung einen Sinn.
Warum erscheint dann in einem klassischen Doppelspalt-Experiment, z.B. mit Laserlicht, die Verteilung so glatt, wie bei Wellen? Weil dort jeweils sehr hohe Teilchenzahlen N beteiligt sind. Es gibt dort zwar auch sehr große statistische Schwankungen ΔN; als grobes Maß nimmt man ΔN = √N, wenn N die Zahl der Teilchen ist, die in einem Flächenstück des Schirms nachgewiesen werden. Mit zunehmender Teilchenzahl wächst diese Streubreite sogar. Aber die relative Streubreite ΔN/N = √N/N = 1/√N wird für sehr große Teilchenzahlen beliebig klein, weil z.B. zwischen 1 000 000 und 1 001 000 oder 999 000 für das Auge kaum ein Unterschied besteht. Für N = 10 ergibt sich noch ΔN/N = 0,3, für N = 1000000 schon ΔN/N = 0,001. Für das Auge sind dann solche Streuungen bei großen Teilchenzahlen nicht mehr sichtbar. Bei Radiowellen mit der extrem kleinen Photonenenergie (typisch: E = 6,6·10-26 J = 4·10-7 eV und der extrem großen Zahl beteiligter Photonen (N typisch 1026 pro Sekunde) sind solche Streuungen nicht mehr nachweisbar: Radiowellen können in extrem guter Näherung als klassische Wellen aufgefasst werden. Genau genommen zeigen sie aber genau das statistische Verhalten, das wir hier beobachtet haben.
Allerdings: Große Teilchenzahlen erklären noch nicht den Übergang von Quanten zu klassischen Wellen. Genaueres dazu hat Glauber (1963) gezeigt. Vgl. kohärente Zustände.
*) Wenn von klassischen Teilchen oder klassischen Wellen gesprochen wird, meint man Teilchen und Wellen, die sich wie (stark verkleinerte) Teilchen oder wie Wellen aus der makroskopischen Physik verhalten, die also bereits durch die Physik des 19. Jahrhunderts beschrieben werden. Zu solchen Wellen gehören etwa Wasserwellen oder Schallwellen. Damals hätte niemand daran gezweifelt, dass sie alle Eigenschaften, die man in der makroskopischen Physik von ihnen behauptete, tatsächlich auch gleichzeitig besitzen.
I.3.5 Deutungsversuch (2):
Sind also Elektronen oder Photonen doch klassische*) Teilchen?
Einteilchen-Interferenz im Unterschied zu
Wellen-Interferenz
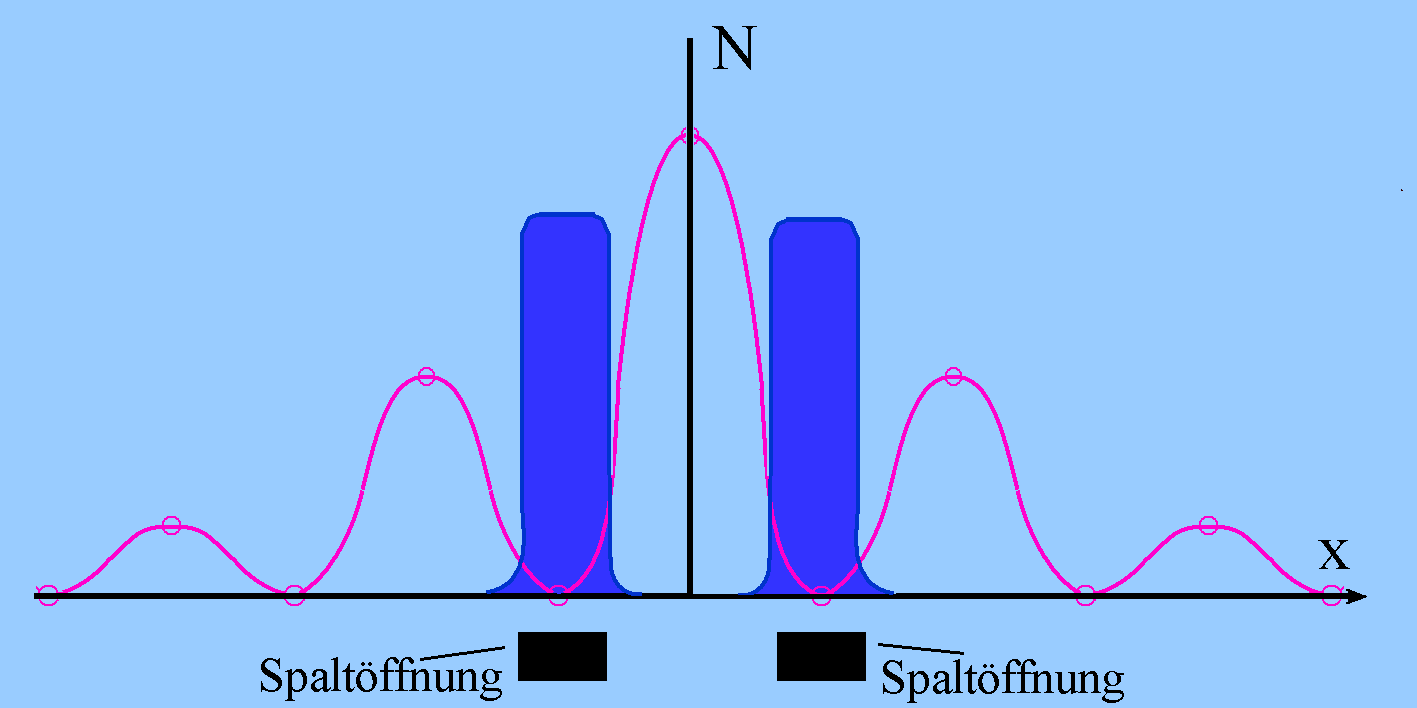 Nein,
die Teilchen werden ganz woanders (lila) nachgewiesen, als es für
klassische*) Teilchen (blau) vorhergesagt ist,
insbesondere gibt es Orte, wo gar keine bzw. sehr wenige Teilchen
(lila) nachgewiesen werden: an den Stellen der Minima.
Nein,
die Teilchen werden ganz woanders (lila) nachgewiesen, als es für
klassische*) Teilchen (blau) vorhergesagt ist,
insbesondere gibt es Orte, wo gar keine bzw. sehr wenige Teilchen
(lila) nachgewiesen werden: an den Stellen der Minima.
Dort hätten sich - bei geeignetem Spaltabstand - klassische Teilchen eventuell sogar mit Vorliebe angesammelt (überwiegend direkt hinter den Spaltöffnungen; blau).
(Wie nun die exakte Verteilung klassischer Teilchen hinter dem Doppelspalt (blau) aussieht, hängt von "Randeffekten" ab, die beeinflussen, ob Teilchen auch etwas in den Schattenbereich hinein abgelenkt werden. Das ist wiederum z.B. von der Größe der Teilchen abhängig.)
|
1.3.6 Vorläufige Folgerung und Deutung mit der "Modellphilosophie"
. .
. . .
|
|
1.3.6 Vorläufige Folgerung und Deutung mit der "Modellphilosophie"
. .
. .
|
|
1.3.6 Vorläufige Folgerung und Deutung mit der "Modellphilosophie"
. .
.
|
(1) Photonen, Elektronen, Atome, Neutronen, Protonen ... sind weder klassische*) Teilchen noch klassische*) Wellen. Licht oder ein elektromagnetisches Feld ist weder eine klassische Welle, noch besteht es aus klassischen Teilchen.
(Ganz entsprechend werden in der Quantentheorie, speziell der Quantenfeldtheorie, auch für Elektronen, Atome, Neutronen, ... Felder eingeführt. Wie für elektromagnetische Felder muss man auch für sie sagen, dass sie weder klassische Wellen sind, noch aus klassischen Teilchen bestehen. Auf eine solche Sichtweise wollen wir hier aber nicht eingehen.)
(2) Dabei hat man aber den Eindruck, dass das Verhalten in manchen Fällen ähnlich ist wie bei klassischen Wellen oder wie bei klassischen Teilchen. Deswegen hat es sich eingebürgert, in manchen Fällen so zu tun, als handele es sich um Wellen und in anderen, als handele es sich um Teilchen. Man spricht von Modellen der Wirklichkeit oder von Bildern, dem "Wellenbild" oder dem "Teilchenbild". Manches kann man mit diesen Modellen (Bildern) sogar quantitativ klären, wie z.B. die Lage der Maxima und Minima der Interferenzfigur mit Hilfe des Wellenmodells. In anderen Fällen versagen solche Modelle aber kläglich.
So ist sich jeder, der mit einem gewissen Recht mit solchen Modellen umgeht, der Tatsache bewusst, dass sie nicht ganz der Wahrheit entsprechen: Photonen, Elektronen, Atome, Neutronen, ... sind weder klassische Teilchen noch klassische Wellen. Aber es ist bequem, mit solchen Modellen zu argumentieren.
|
Kernaussage der "Modellphilosophie" zur Quantenphysik: "Welle" und "Teilchen" sind Hilfsvorstellungen bzw. Modelle, um bestimmte Versuche anschaulich und qualitativ deuten oder mit Worten beschreiben zu können. In beschränktem Maße können sie auch bestimmte quantitative Vorhersagen machen. Sie sind der Natur nur teilweise angemessen. |
(3) Welches Modell man zur Beschreibung wählt, ist eine Frage der Zweckmäßigkeit, nicht eine der Notwendigkeit, die sich aus der jeweiligen Versuchsanordnung oder aus einer "Natur" oder einem "Charakter" der Teilchen ergäbe. Man nimmt das Modell, mit dem sich ein Sachverhalt einfacher formulieren, beschreiben, ausdrücken, ... lässt. Manche Versuche lassen sich sogar mit beiden Modellen qualitativ deuten, z.B. Interferenzen am Beugungsgitter (Duane 1923) oder der Compton-Effekt (Compton 1923), wenn auch evtl. sehr kompliziert.
Zur qualitativen Deutung von manchen anderen Experimenten scheint es sogar zweckmäßig, beide Modelle nebeneinander anzuwenden, wie z.B. beim Doppelspalt, wenn in einer Messung festgestellt wird, durch welchen Spalt das Teilchen hindurch getreten ist. Dann scheint das Teilchenbild naheliegend, weil die Doppelspalt-Interferenz verschwunden ist, aber es gibt immer noch Beugung und Interferenz an jedem der Einfachspalte (Beugung am Einzelspalt trotz Welcher-Weg-Information, welche die Doppelspalt-Interferenz verhindert).
Ein anderes Beispiel ist die " Strahlung schwarzer Körper ", wo Einstein nach der Entdeckung der richtigen Gesetzmäßigkeit durch Planck die bekannten Näherungsgesetze von Wien und Rayleigh-Jeans als Grenzfälle reproduzieren konnte, wenn er sie als Folge des Teilchenmodells und des Wellenmodells für die Strahlung interpretierte. (Das relative Schwankungsquadrat der Energie setzt sich nach Einstein aus einem reinen Teilchenanteil und einem reinen Wellenanteil zusammen.)
Quantitativ gelingt die Erklärung aber in der Regel mit keinem dieser anschaulichen Modelle ganz.
(4) Zu vollständigen und quantitativen Aussagen braucht man die korrekte Quantentheorie. Diese beruht auf keinem dieser Modelle, ist nicht anschaulich, und darf es prinzipiell auch nicht sein.
Photonen, Elektronen, Atome, Neutronen, ... sind nun mal weder klassische Teilchen noch klassische Wellen.
(5) Diese hier erläuterte "Modellphilosophie" ist aber nur ein Teil der Wahrheit. Sie klärt einen häufigen Sprachgebrauch, der eben geeignet sein kann, wenn ein Experiment eher qualitativ beschrieben werden soll, macht aber keine Aussage darüber, was nun wirklich vorgeht, oder wie eine korrekte Quantenphysik mathematisch zu formulieren ist.
I.3.7 Versagen der "Modellphilosophie" bei Zweiteilchen-Zuständen (verschränkten Zuständen)
Ähnliches gilt aber auch für den Zwei-Elektronen-Zustand, durch den die Elektronenhülle eines He-Atoms beschrieben wird (wenn man es korrekt machen möchte), und für andere Vielteilchen-Zustände bei Mehrelektronen-Atomen.
Obwohl der Name verführerisch auf zwei Teilchen hinweist, muss man mit den verwendeten Modellen sehr vorsichtig sein:
- Ein naives Wellenmodell (mit Wellen im
dreidimensionalen Anschauungsraum) versagt ganz;
Wahrscheinlichkeitsaussagen für viele mögliche Messergebnisse
erhält man - wie die gesicherte Quantentheorie lehrt -
erst dann, wenn man Wellen in mindestens 6-dimensionalen
Räumen betrachtet: Es besteht keine Hoffnung, hier anschaulich
argumentieren zu können.
- Ein naives Teilchenbild, nach dem man sich etwa zwei konkrete mehr oder weniger klassische Teilchen mit irgendwelchen "Verwandtschaften", also aufeinander bezogenen festen Eigenschaften, schon bei der Entstehung der Teilchen in der Quelle vorstellt, versagt, weil dann die Teilchen wirklich merkwürdige Eigenschaften haben müssten: Wir werden bald sehen: Schon ein einzelnes Teilchen hat nicht alle klassisch denkbaren Eigenschaften gleichzeitig, aber jede Eigenschaft kann durch eine Messung einen Sinn erhalten. Führen wir also bei einem Elektronen- oder Photonenzwilling eine Messung einer derartigen Eigenschaft an einem Teilchen durch, die das Teilchen erst durch die Messung erhält, muss auch das zweite Teilchen eine entsprechende Eigenschaft erhalten. Die Messung an einem Teilchen müsste dann im gleichen Moment ("instantan") die Eigenschaften auch des anderen beeinflussen/festlegen/be-stimmen, selbst wenn sich dieses am Rande unseres Weltalls befindet. Es müsste dann (unter der Annahme eines naiven Teilchenbilds) eine Wirkung mit Überlichtgeschwindigkeit auf das zweite Teilchen übertragen werden, was gesicherten Erkenntnissen der Relativitätstheorie widerspricht. Es geht aber nicht um eine Fernwirkung. Man spricht sogar manchmal von einer Fernwirkungslosigkeit.
Tatsächlich haben vor einer Messung von Eigenschaften eines einzelnen Teilchens die beiden Teilchen in einem Zweiteilchen-Zustand keine individuelle Existenz (keinen Sinn, keine be-stimmten Eigenschaften). Als zwei Teilchen, wie wir sie uns vielleicht vorstellen wollen, entstehen sie erst, wenn durch eine Messung nach Eigenschaften von einem von ihnen gefragt wurde. Erst dann wird der Zweiteilchen-Zustand in zwei Einteilchen-Zustände "zerlegt", für die ein Teilchenmodell in einem gewissen Sinn passen könnte. Das Teilchenmodell für jedes von ihnen im Zweiteilchen-Zustand würde mit Sicherheit zu scheinbaren Paradoxa und Missverständnissen führen, wie wir gerade gesehen haben. Ein Zweiteilchen-Zustand (verschränkter Zustand) lässt sich trotz des Namens eben weder durch ein (naives) Wellenmodell noch durch ein (naives) Teilchenmodell sinnvoll beschreiben. Beide Modelle versagen hier. Mehrteilchen-Zustände oder "Verschränkte Zustände" haben kein klassisches Analogon! Auf solche "verschränkten Zustände" muss später noch genauer eingegangen werden.
Ich möchte sogar so weit gehen zu behaupten, dass man die Quantentheorie nur eingeschränkt verstehen kann, wenn man Zwei-Teilchen-Zustände nicht verstanden hat.
Übrigens, neben der bisher besprochenen Einteilchen-Interferenz beim Doppelspalt gibt es auch eine Zwei-Teilchen-Interferenz beim "Doppel-Doppelspalt" (vgl. auch "Malvern-Experiment" und Berkeley-Quantenauslöscher), die gerade die merkwürdigen Eigenschaften eines Zwei-Teilchen-Zustands benutzt, und natürlich Wellen-Interferenz.
Zeilinger: "Das Teilchen" - ich möchte ergänzen 'und die Teilchen' - "kümmert (kümmern) sich ganz offensichtlich nicht darum, welches Bild wir uns von ihm (ihnen) machen wollen."