Es handelt sich um ein Interferometer aus 3 Gittern mit gleichen Spaltabständen d. Auch die Abstände der Gitter sind gleich und entsprechen der "Talbot-Länge" L = 2·d²/λ). Das Verfahren ähnelt der Situation beim Aharonov-Bohm-Effekt mit Elektronen.

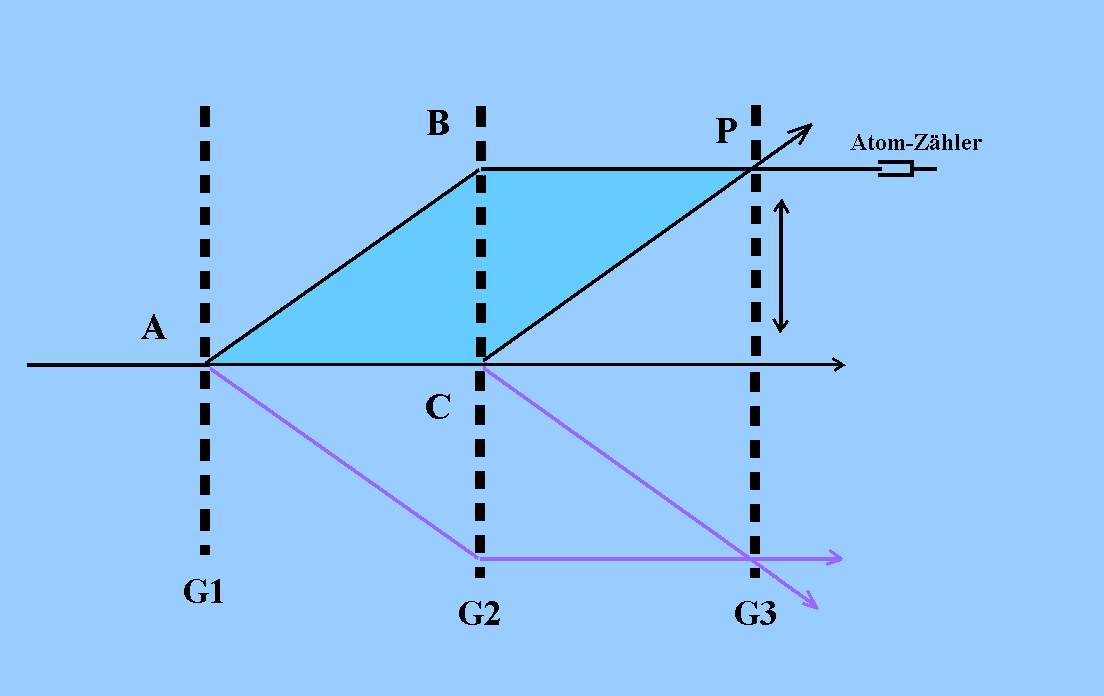
Abb. 1:

(1) Ein gebündelter und möglichst monochromatischer Strahl von Atomen fällt senkrecht auf das Gitter G1. Der Strahl spaltet sich durch Beugung und Interferenz an G1 (z.B. an der Öffnung A) auf in die Maxima der verschiedenen Ordnungen (nur die 0. und die zwei 1. Ordnungen sind gezeichnet). Am Gitter G2 findet das gleiche statt. (An seiner Position entsteht ein "Talbot-Bild" von G1 mit gleicher Gitterkonstanten d.) Aus Symmetriegründen muss u.a. bei B eine horizontale Ablenkung erfolgen, bei C in die gleichen Richtungen wie bei A. Es entsteht u.a. ein Parallelogramm ACPB. Denken Sie sich zunächst das Gitter G3 weg. An seiner Stelle entsteht ein weiteres Talbot-Bild von G1, z.B. mit einer Öffnung an der Stelle P und Hindernissen dicht daneben. Es hat die gleiche Gitterkonstante d wie die anderen Gitter.

(3) Man stellt nun einen Atomzähler in einigem Abstand vor G3 auf, der nur für eine Austrittsrichtung empfindlich ist, z.B. die achsenparallele. Man sucht eine Position aus mit maximaler Zählrate, also z.B. vor P. Stellt man nun das Gitter G3 ein und verschiebt es, so kann man alle horizontalen Strahlen blockieren oder freigeben. Dementsprechend variiert die Zählrate. Das ist ein Nachweis für die Interferenzfähigkeit  monochromatischer Atome.

(2) Nach der Zeichnung entsteht bei P das Bild einer Öffnung von G1 (A). Hat G3 die gezeichnete Position können Atome z.B. in die gezeichneten Richtungen austreten.

Hier wird keine Fernfeld-Interferenz erzeugt, wie z.B. bei der Fraunhoferschen Beugung mit ebenen Wellenfronten, sondern Nahfeld-Interferenz mit gekrümmten Wellenfronten. Das spielt aber eine untergeordnete Rolle, weil nach den bisherigen Erläuterungen eine Auswertung zur Wellenlängenmessung ohnehin nur indirekt möglich ist. Die so definierten Maxima haben alle den Abstand d, unabhängig von der deBroglie-Wellenlänge.

Die Bedeutung des Versuchs liegt darin, dass die Lage der Maxima (z.B. der Punkt P) in Querrichtung von der Phasenverschiebung der zwei interferierenden Strahlen abhängt auf ihren klassisch denkbaren Wegen ABP und ACP. Und die kann beeinflusst werden, z.B. durch eine Beschleunigung der Apparatur in Querrichtung oder eine Rotation um eine Achse senkrecht auf der Parallelogramm-Ebene. So hat man ein extrem empfindliches Messgerät für Beschleunigungen zur Verfügung, z.B. als Gravitationswellenmesser, oder für Rotationsgeschwindigkeiten. Verschiebung von G3 bedeutet also Phasenmessung.

Für die Rotation lässt sich das für eine leicht andere Situation elementar abschätzend einsehen.

Das Talbot-Lau-Interferometer kommt mit größeren Spaltabständen d aus und erlaubt deshalb Interferenzversuche mit noch größeren Massen als mit Fulleren-Molekülen (z.B. C₆₀). Z.B. wurden schon C₆₀F₄₈ mit ca. doppelter Masse oder der Biofarbsstoff TTP (Tetraphenyl-Porphyrin) eingesetzt ^*)  und damit deren Interferenzfähigkeit bewiesen. Manche Leute würde dafür die problematische Formulierung verwenden: "Es wurde der Wellencharakter dieser Moleküle bewiesen".

E

1. Auch mit sehr großen einzelnen Molekülen wie Fulleren-Molekülen oder noch massereicheren ist Interferenz möglich. 2. Interferenz von Atomen kann für die präzise Messung von Beschleunigungen und Winkelgeschwindigkeiten eingesetzt werden. 3. Falls eine Situation vorliegt (hohe Temperatur), in der die Moleküle Weginformation durch die abgegebene Infrarot-Strahlung abgeben könnten, findet "Dekohärenz" statt und die Interferenz verschwindet. Durch die Infrarot-Photonen ist ein großes Molekül an die Umgebung angekoppelt, durch die es aus einem Zustand mit un-be-stimmten Eigenschaften in einen Zustand mit be-stimmten Eigenschaften innerhalb sehr kurzer Zeit übergeht. In diesem Fall verhalten sich dieselben Quantensysteme wie makroskopische klassische Teilchen.

^*) L. Hackermüller et al., Phys.Rev.Lett. 2003, 91, 090408.

Wir ersetzen das Parallelogramm durch einen Kreis. P soll der Quelle Q genau gegenüberliegen. Im nicht rotierenden System brauchen die Atome von S nach P die Zeit t = r·π/v. Bei Rotation mit der Winkelgeschwindigkeit ω hat sich aber P im Laborsystem in dieser Zeit weiterbewegt, sodass der eine Weg um die Strecke r·ω·t = r²·π·ω/v länger, der andere um die gleiche Strecke kürzer erscheint. Es entsteht ein Wegunterschied von 2· r²·π·ω/v , der einer Differenz von 2· r²·π·ω/(v·λ) ganzen deBroglie-Wellen λ entspricht. Es ergibt sich ein Gangunterschied von 2·A·ω /λ·v = 2·A·ω·m/h ganzen Wellenlängen. Nehmen wir an, bei P sei ohne Rotation ein Maximum. Dann liegt mit Rotation dort ein Minimum, wenn der Gangunterschied eine halbe Wellenlänge beträgt. A = r²·π ist dabei die eingeschlossene Fläche, m die Atommasse, h das Planck'sche Wirkungsquant. Der Gangunterschied ist also proportional zu ω, wie auch die genaue und allgemeinere Theorie bestätigt.