Prinzipversuch nach Grangier, Roger und Aspect (GRA 1986), zitiert nach Zeilinger, vgl. auch Schülerglossar.

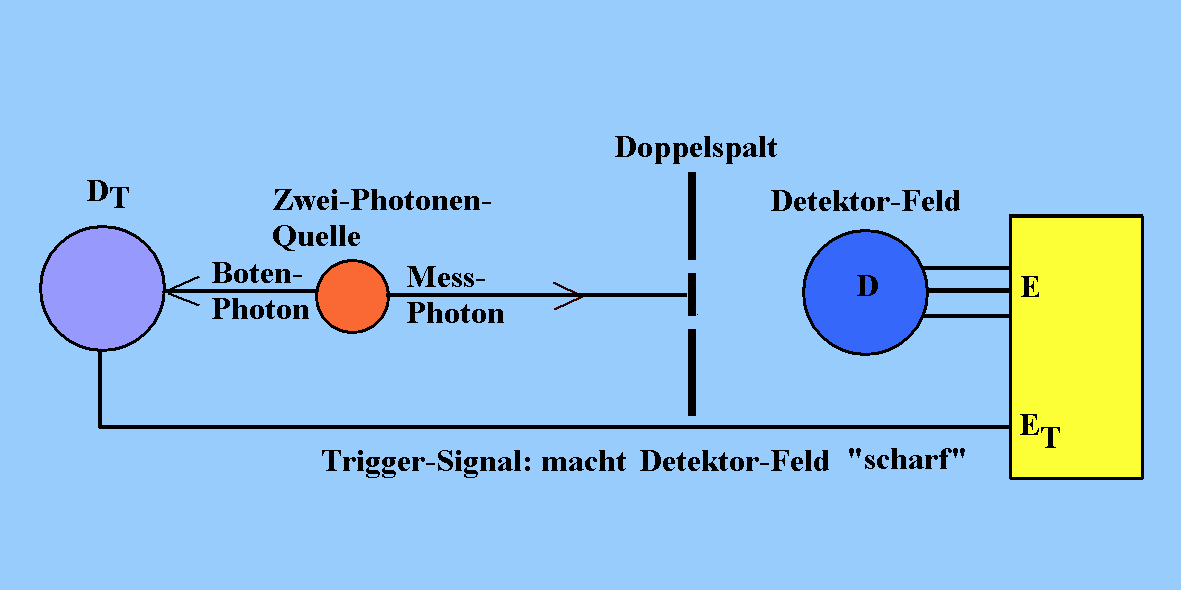
(1) Es wird ein Doppelspalt-Versuch mit einzelnen Photonen durchgeführt. Um sicher zu gehen, dass wirklich immer nur ein Photon in der Apparatur ist, wird eine Zwei-Photonen-Quelle verwendet, die quasi gleichzeitig zwei Photonen emittiert. Bei abgeschwächtem Laserlicht*) kann man nicht aussschließen, dass zwei Photonen gleichzeitig auf den Doppelspalt treffen. Das eine Photon  ("Messphoton") soll die Quanteninterferenz durchführen, das "Botenphoton" signalisiert, dass jetzt genau ein Photon "unterwegs" ist.

(2) Mit dem Detektor-Feld wird auf einem "Schirm" wie beim normalen Doppelspalt-Versuch jeweils ein Photon nachgewiesen und sein Ort registriert, nachdem eine Koinzidenz-Apparatur durch das gleichzeitig entstandene "Botenphoton" "scharf geschaltet" wurde.Wenn ein Lautsprecher angeschlossen wäre, würde es bei jedem Nachweis eines einzelnen Photons genau einmal "Klick" machen. (3) Jedes einzelne Photon wird als Ganzes irgendwo auf dem Schirm registriert, an zufälligen Orten, vor allem in der Nähe der Maxima einer gedachten Interferenzfigur. Aber, wenn der Versuch sehr häufig wiederholt wird mit sehr viel Mess-Photonen aus der Zwei-Photonen-Quelle, baut sich so nach und nach eine Interferenzfigur aus lauter Einzelnachweisen auf. (4) Die Quelle muss  räumliche Kohärenz garantieren und sie muss so klein sein, dass keine Aussage über den Weg des Mess-Photons aus dem Boten-Photon abgeleitet werden kann. Das Boten-Photon hat nur die Aufgabe, die Anwesenheit eines einzigen Mess-Photons in der Anordnung zu signalisieren.

E	Interferenz kommt bereits mit einem einzigen Photon zustande, weil es zwei klassisch denkbare Möglichkeiten für den Weg des Photons durch die beiden Spaltöffnungen gibt, zwischen denen nicht unterschieden wird.

Beim Ostermeyer-Versuch wird (im Prinzip) ein Doppelspalt-Versuch mit Biphotonen (Photonenzwillingen) durchgeführt, also nicht, wie hier, mit einzelnen Photonen.

^*) Auch nach dem Durchtritt durch ein Graufilter bleibt kohärentes Licht kohärent. Dabei genügt die Zahl der Photonen in jedem Zeitabschnitt immer noch einer Poisson-Verteilung.