Beim Doppelspalt-Versuch liefert die Rechnung ein Maximum, wenn der Gangunterschied der sich überlagernden Wellen(pakete) ein ganzzahliges Vielfaches der Wellenlänge ist. Aber nicht in jedem Fall beobachtet man an einer solchen Stelle tatsächlich ein Maximum, besonders unter größeren Ablenkungswinkel fehlen häufig berechnete Maxima.

Zwischen den sich überlagernden Lichtstrahlen muss eine zeitlich feste Phasenbeziehung bestehen ("Kohärenzbedingung"). Eine weitere Voraussetzung für die Interferenz ist, dass sich die beiden Wellenzüge tatsächlich überlagern ("Koinzidenzbedingung" oder "zeitliche Kohärenz"). Wenn es sich aber um endliche Wellenzüge handelt, könnte am Beobachtungspunkt ein Wellenzug schon passiert sein, während der zweite noch gar nicht eingetroffen ist. Das kann sich besonders bei großen Ablenkungswinkeln ereignen, wenn der Gangunterschied groß und die Länge der Wellenzüge klein ist. Deswegen hat man den Begriff der Kohärenzlänge eingeführt, der der mittleren Länge der Wellenzüge entspricht.

Bei Photonen lässt sich die Kohärenzlänge leicht berechnen: Dauert der Emissionsvorgang im Mittel die Zeit Δt, dann kann die Länge des Wellenzugs aus der Lichtgeschwindigkeit berechnet werden:

Δx = c·Δt

Bei einer typischen Dauer von 10^-14 s für einen Emissionsvorgang in einer Glühlampe etwa ergibt sich damit eine Kohärenzlänge von 3 ·10^-3 mm. Bei Laserlicht kann die Kohärenzlänge gut 300 m sein, was einer 10⁸ mal größeren Lebensdauer des strahlenden Übergangs entspricht.

Gemäß der HUR hängt die Dauer des Emissionsvorgangs eng mit der Linienbreite zusammen:      

Δf · Δt >= 1/2p       bzw.      ΔE · Δt >= h = h/2p

Neben der zeitlichen Kohärenz, die mit der (longitudinalen) Kohärenzlänge zusammenhängt, gibt es noch eine räumliche Kohärenz.

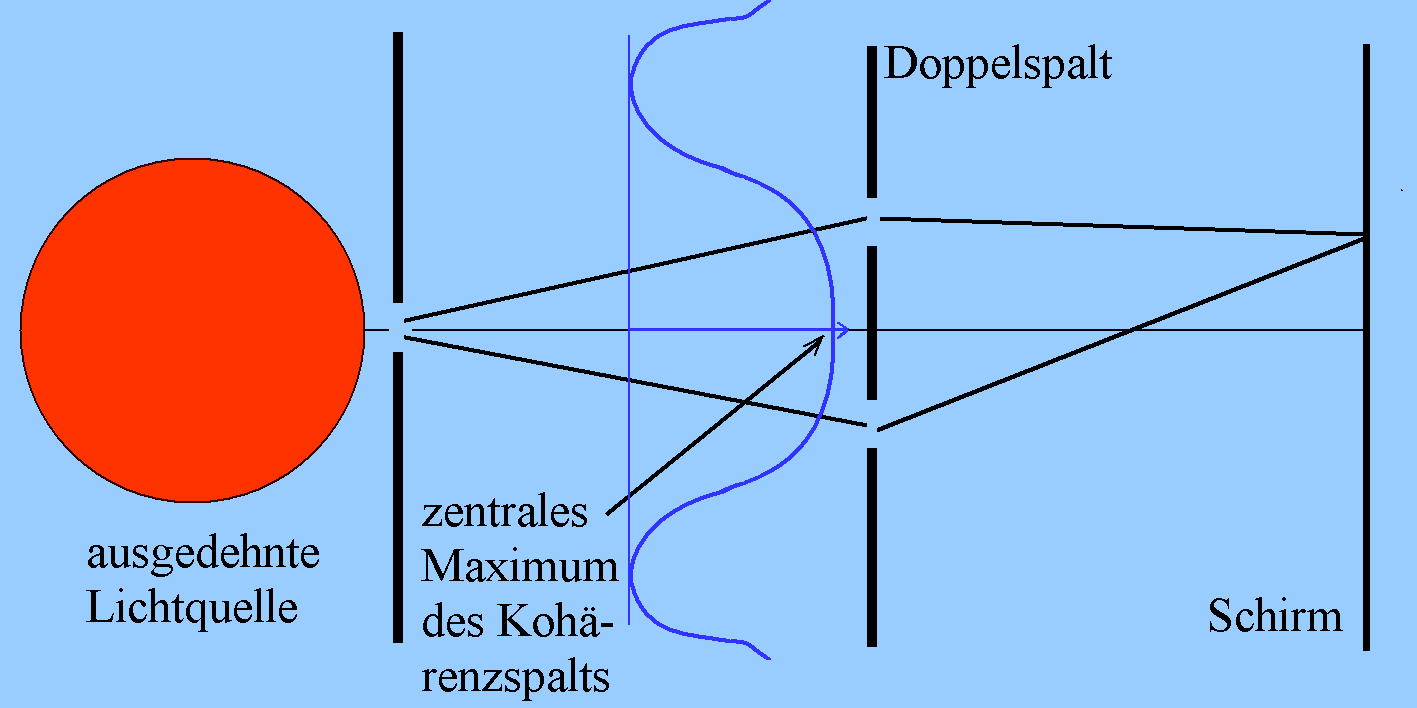
Bei einer ausgedehnten Lichtquelle, wie etwa der Sonne, strahlen weit entfernte Atome vollkommen unabhängig voneinander ihr Licht ab. Die Wahrscheinlichkeit, dass sich die ausgesandten Wellenpakete nach dem Doppelspalt auf dem Schirm tatsächlich überlappen, ist also sehr gering. Verkleinert man jedoch die Lichtquelle künstlich durch einen Kohärenzspalt, dann entsteht Beugung am Einfachspalt mit einem zentralen Maximum. Wo auch immer die beitragenden Lichtstrahlen herkamen, sie müssen gleichphasig sein, sonst würden sie nicht zum zentralen Maximum beitragen.

Sorgt man jetzt dafür, dass das zentrale Maximum vom Kohärenzspalt die beiden Spalte eines Doppelspalts gemeinsam ausleuchtet, so ist Doppelspalt-Interferenz möglich, weil das Licht durch den Kohärenzspalt räumlich kohärent gemacht wurde ("Sichtbarkeitsbedingung"). Im Zusammenhang damit steht auch eine "transversale Kohärenzlänge". Sie misst beim Doppelspalt, Detektor, ...  den Bereich quer zur Ausbreitungsrichtung, in dem bei einer  ausgedehnten Lichtquelle gerade noch Interferenzen sichtbar sind.