I.6.1 Tiefergehende Deutung des Doppelspalt-Versuchs und der Quantenphysik . . . .. . . . . . . . . . . I.6.1 Tiefergehende Deutung des Doppelspalt-Versuchs und der Quantenphysik . . . . . . ... . . . . . . . . . . . . . I.6.1 Tiefergehende Deutung des Doppelspalt-Versuchs und der Quantenphysik . . . . . . . . . . . . . .	Stellen wir die wichtigsten unserer Erkenntnisse noch einmal zusammen, die wir auch als Grundfakten der Quantenphysik formulieren wollen: (1) Alle klassisch denkbaren Eigenschaften eines Quantensystems können gemessen werden. Messen heißt, eine Frage an die Natur stellen im Sinne von makroskopisch definierten Begriffen, etwa in dem Sinn „Elektron, angenommen du hast einen Ort, wo bist du dann?“ Die Natur reagiert darauf in jedem Fall mit einer eindeutigen Antwort. (Siehe Grundfaktum Ib: Messbarkeit aller klassisch denkbaren Eigenschaften und Grundfaktum IVa) Aber: (2) Ohne Messung hat es keinen (physikalischen) Sinn, von einer bestimmten Eigenschaft eines Mikroojekts zu sprechen; erst durch eine Messung wird i.A. die Eigenschaft des Quantensystems be-stimmt. Eine solche Eigenschaft heißt vor der Messung objektiv un-be-stimmt. Das gehört zu den wichtigsten Dingen, die die Quantenphysik von der klassischen Physik unterscheidet, ein Faktum, an das man sich gewöhnen muss. (Siehe Grundfaktum Id: objektive Un-be-stimmtheit) (3) Nicht alle klassisch denkbaren Eigenschaften sind bei Quantensystemen gleichzeitig erfüllt, beim Doppelspalt-Versuch z.B. nicht Durchtrittsort und Interferenzfähigkeit gleichzeitig, oder Ort und Geschwindigkeit eines Teilchens gleichzeitig; der "objektive Zufall" ist eine Folge davon. Paare von Eigenschaften, die sich gegenseitig ausschließen, heißen komplementär. (Siehe Grundfaktum Ia: Nichtexistenz aller klassisch denkbaren Eigenschaften gleichzeitig) (4) Eigenschaften, die ein Quantensystem im betreffenden Zustand tatsächlich besitzt ("be-stimmte" Eigenschaften), führen zu  immer gleichen Messwerten, falls sich der Zustand des Systems zwischen den Messungen nicht verändert hat. Messungen der jeweils dazu komplementären Eigenschaften ergeben streuende Messwerte, die dem "objektiven Zufall" unterliegen. Ursache ist die objektive Un-be-stimmtheit dieser zweiten Gruppe von Messgrößen (bei Be-stimmtheit der ersten Gruppe). Die Natur reagiert auf die oben gestellte Frage nach dem Ort eines Elektrons unterschiedlich. Wenn das Elektron  in einem Zustand ist, in dem es die Eigenschaft "be-stimmter Ort" hat, dann gibt sie auch die richtige Antwort, und die immer wieder, wenn sich der Zustand nicht dazwischen verändert. Ist das Quantensystem aber in einem Zustand, in dem es diese Eigenschaft nicht hat, dann reagiert die Natur auf die nicht ganz passend gestellte Frage mit streuenden Antworten, einmal mit diesem Ergebnis, einmal mit jenem: zwangsläufig streuen in vielen Fällen die Messwerte selbst bei größter Messgenauigkeit statistisch um einen Mittelwert *). Wenn von einem Teilchen der Impuls be-stimmt wurde, ist der Ort un-be-stimmt. Ortsmessungen an jeweils gleich präparierten Teilchen mit gleichem Impuls liefern dann zufällig verteilte Orte.Wenn von einem Teilchen der Ort be-stimmt wurde, ist der Impuls un-be-stimmt. Impulsmessungen an jeweils gleich präparierten Teilchen mit gleichem Ort liefern dann zufällig verteilte Impulse. (Siehe Grundfaktum Id: objektive Un-be-stimmtheit) (Siehe Grundfaktum IIb: objektiver Zufall) (5) Wir haben bereits festgestellt: Alle klassisch denkbaren Eigenschaften können im Experiment be-stimmt werden. Die Folge ist aber ein Eingriff der Messung in das System, indem es eben die betreffende Eigenschaft be-stimmt macht, die vorher nicht in jedem Fall be-stimmt war. Die Wirkung des Eingriffs ist deshalb nicht beliebig klein zu machen. Wenn eine Messung des Durchtrittsorts beim Doppelspalt durchgeführt wurde, war dazu eine ganz andere Anordnung nötig als für die Beobachtung der Interferenz.  Deshalb kann man nicht von der einen Beobachtung (Durchtrittsort) auf eine andere (Interferenzfigur) schließen. (Siehe Grundfaktum Id: unvermeidbarer Eingriff) (Siehe Grundfaktum Ib: Messbarkeit aller klassisch denkbaren Eigenschaften) (Siehe Grundfaktum IVa: Alle makroskopisch sinnvollen Eigenschaften sind messbar ) (6) Die Quantentheorie macht gesetzmäßige Aussagen über alles, was physikalisch real ist. Sogar dann, wenn sich das System bzgl. einer Messgröße A in einem Überlagerungszustand befindet, wenn also die betrachteten Eigenschaft zunächst nicht erfüllt ist, gehören dazu die mögliche Messwerte  für solche - zunächst un-be-stimmten - Eigenschaften. In diesem Fall gehören auch die objektiven Wahrscheinlichkeiten für das Eintreten solcher Messwerte dazu.  (Siehe Grundfaktum II: objektive Wahrscheinlichkeit) (7) Im Doppelspalt-Versuch beobachteten wir die " Interferenz von Möglichkeiten ", die sich überlagern. Davon ist i.A. keine realisiert. (Zeilinger: "die Natur hat sich noch nicht entschieden"). Ein Teilchen durch den Doppelspalt hat - klassisch gesprochen - die Möglichkeit des Wegs durch Spalt A oder durch Spalt B. In der Quantenphysik  müssen wir feststellen, dass es keinen Weg durch den einen Spalt oder den anderen "hat", außer, wenn man einen solchen misst. Ohne Messung hat es keinen Sinn, vom Weg eines Teilchens durch den Doppelspalt zu sprechen. Allgemein findet Interferenz nicht etwa statt, weil sich zwei oder mehr realistische (materielle) Wellen irgendwie "zusammenlegen", sondern weil eine Konkurrenz zwischen nicht unterschiedenen klassisch denkbaren Möglichkeiten besteht. (Siehe Grundfaktum III: "Interferenz von Möglichkeiten") (8) Besondere Überlegungen erfordert ein möglicher Doppelspalt-Versuch mit Teilchenzwillingen (Doppel-Doppelspalt-Versuch).  Er lässt sich nicht als zwei hintereinander oder parallel durchgeführte Doppelspalt-Versuche mit einzelnen Teilchen deuten. Er bestätigt das Grundfaktum V (Quantenmechanische Nichtlokalität ). (0) Eine Sache ist bisher noch nicht zur Sprache gekommen: Welche Fragen an die Natur können wir sinnvollerweise überhaupt stellen? Wir wollen die Antwort als Grundfaktum 0 bzw. Präambel formulieren: Wissenschaftler überlegten sich: Die Physik darf nur Aussagen machen über Dinge, die durch reale Messungen überprüfbar sind. Dazu braucht man reale Messgeräte, also makroskopische Geräte. Diese Forderung liegt auch der Quantentheorie zugrunde - ebenso wie der Relativitätstheorie. Mit Messgeräten kann aber prinzipiell nur nach Messgrößen bzw. Begriffen gefragt werden, die außerhalb der atomaren Größenordnungen bewährt sind, also z.B. nach Ort und Geschwindigkeit oder den Drehimpuls eines Teilchens, so als ob es ein makroskopisches Teilchen wäre. Für den atomaren Bereich haben diese Begriffe nur mehr einen beschränkten Sinn. So gibt es ja, wie wir wissen, zum Beispiel im atomaren Bereich keine Bahn eines Photons von der Lichtquelle zum Nachweisort als Aufeinanderfolge von Orts-Geschwindigkeits-Situationen.Und bzgl. des Drehimpulses gibt es in Form des Elektronenspins Überraschungen. Diese Feststellung ist wesentlicher Kern der Kopenhagener Deutung der Quantentheorie, die in den zwanziger und dreißiger Jahren des 20. Jahrhunderts in Kopenhagen von einem Kreis um Niels Bohr entwickelt worden ist, dem auch Werner Heisenberg und Max Born und andere angehörten. Diese Feststellung hätten wir allen Grundfakten vorausschicken müssen; deswegen geben wir dem Abschnitt nachträglich die Nummer (0).
I.6.2 Exkurs: Beschreibung von Quantensystemen durch Zustände	Mit dem Begriff eines quantenphysikalischen Zustands lassen sich viele Erscheinungen der Quantenphysik leichter und klarer formulieren. Was ist ein Zustand? Ein Zustand ist etwas sehr Abstraktes, das durch eine vollständige Liste aller Eigenschaften beschrieben wird, die ein System tatsächlich in der betrachteten Situation (z.B. Versuchsanordnung) besitzt. Ein Zustand ist sozusagen die vollständige Zusammenfassung aller tatsächlichen Eigenschaften des betrachteten Systems in der betrachteten Situation. Das setzt voraus, dass das System in diesen Zustand vorher "präpariert" worden ist, z.B. durch eine bestimmte Versuchsanordnung, die nur Teilchen mit bestimmten Eigenschaften durchlässt. Komplementäre Messgrößen können nicht gleichzeitig einen Zustand beschreiben. Eine Sonderrolle spielen Eigenzustände (Das Quantensystem hat eine bestimmte Eigenschaft.) Überlagerungszustände ("Die Natur hat sich noch nicht entschieden.") Verschränkte Zustände (Es ist un-be-stimmt, wie die Eigenschaften eines Mehrteilchen-Systems durch einzelne Teilchen oder Teile eines komplexeren Systems realisiert werden.) Teilchen-Zustände (Die Teilchen-Zahl ist be-stimmt.) Kohärente Zustände (Die Teilchen-Zahl ist völlig un-be-stimmt.) Ein Zustand mit be-stimmten Eigenschaften, also ein Eigenzustand zu einer bestimmten Messgröße A, ist gleichzeitig bzgl. einer dazu komplementären Messgröße C ein Überlagerungszustand, der Beimischungen von alle möglichen Werten c von C enthält. Beispiele: Ein Zustand mit einer be-stimmten Polarisation eines Photons bzgl. eines Polarisators PO, der also ein Photon beschreibt, das den Polarisator PO passiert hat, lässt zu, dass das Photon anschließend durch einen Analysator AN mit weitgehend beliebigem Drehwinkel f hindurchgeht. Der Ausgangszustand des durch PO polarisierten Photons enthält nämlich Beimischungen von allen Polarisationen bzgl. beliebiger Analysator-Stellungen AN. Eine passt dann schon zur Analysatorstellung und ermöglicht den Durchtritt. Die Wahrscheinlichkeit für das Passieren hängt in diesem Fall allerdings vom Drehwinkel f ab. Ein extremes Beispiel dazu ist ein freies Teilchen mit be-stimmtem Impuls. Die komplementäre Eigenschaft "Ort des Teilchens" ist dabei völlig un-be-stimmt. Sein Zustand kann - im Prinzip - auch ausgedrückt werden als Überlagerungszustand von beliebig vielen Zuständen mit be-stimmten Orten. Ganz entsprechend  lässt sich - wenigstens im Prinzip - auch ein freies Teilchen mit be-stimmtem Ort, also ein lokalisiertes Teilchen, präparieren. Die komplementäre Eigenschaft  "Impuls des Teilchens" bzw. "Geschwindigkeit" sind völlig un-be-stimmt. Sein Zustand kann auch ausgedrückt werden als Überlagerungszustand von beliebig vielen Zuständen mit be-stimmten Impulsen. Ein (verschränkter) Zwei-Teilchenzustand wie für einen Photonenzwilling oder einen Elektronenzwilling ist gekennzeichnet durch Eigenschaften des Gesamtzustands, z.B. Gesamtimpuls = 0, Gesamt-Spin = 0, Teilchenzahl = 2. Die letzte Eigenschaft besagt nicht, dass der Zustand zwei individuelle Teilchen beschreibt, die schon ohne eine Messung vorhanden wären. Sie besagt lediglich, dass dann, wenn die Teilchenzahl in einer Messung real bestimmt wird, sich immer 2 ergibt. (Erst nach einer solchen Messung liegen dann wirklich zwei einzelne Teilchen vor.)
I.6.3 Modell zum Verständnis der Rolle der Kausalität bzw.  Nichtkausalität in der Quantenphysik	Zustände entwickeln sich nach der Quantentheorie aus einem vorgegebenen Anfangszustand streng kausal mit unveränderten Eigenschaften bis zu einer Messung. Betrachten wir einen Eigenzustand zu einer bestimmten Messgröße A. In Eigenzuständen ergeben sich bei Messungen von A immer die gleichen Eigenwerte, z.B. a. Sie und andere gleichzeitig messbaren  (z.B. Messgröße B mit dem Wert b) sind die unveränderlichen Eigenschaften des Systems in diesem Zustand, also Eigenschaften, die das System jetzt gleichzeitig hat. Man erhält bei den Messungen am unveränderten oder immer wieder gleich präparierten System immer dieselben Eigenwerte. (Siehe Grundfaktum IVb: Messwerte sind reproduzierbar ) (Siehe Grundfaktum IVc: Eigenwerte) 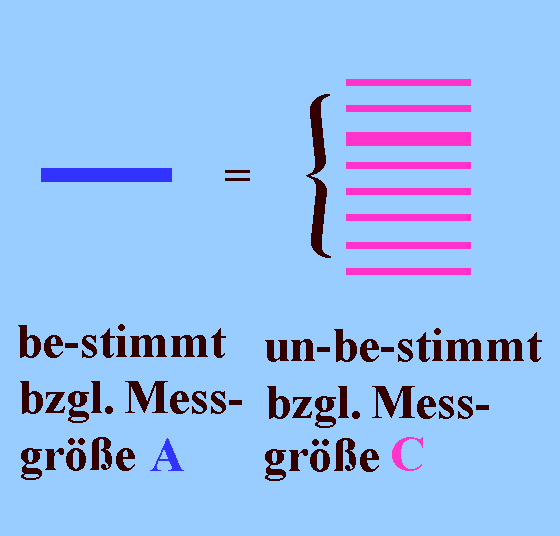Solche Zustände sind bzgl. anderer, komplementärer Eigenschaften, der Messgröße C etwa, Überlagerungszustände, d.h. die selben Zustände lassen sich zugleich durch Beimischungen von Anteilen zu allen möglichen Messwerten c der Messgröße C ausdrücken. Auch die den Eigenzuständen entsprechenden Überlagerungszustände entwickeln sich kausal mit den Eigenzuständen. Wenn das System bzgl. einer Messgröße A in einem Eigenzustand ist, dann ist es bzgl. einer dazu komplementären Messgröße C in einem Überlagerungszustand. Durch Interferenz aller beteiligten und hier überlagerten Eigenzustände zu C entsteht der Ausgangszustand, also der Eigenzustand bzgl. A. (Siehe Grundfaktum IVd: Überlagerungsprinzip) Führt man jetzt aber eine Messung bzgl. einer komplementären Messgröße C durch (also einer Eigenschaft, die das System jetzt nicht hat), wird bei der Messung aus dem Überlagerungszustand bzgl. C ein Zustand mit einem be-stimmten Wert von C ausgewählt, z.B. mit dem Messwert c. Dieser Auswahl-Vorgang ist nicht mehr kausal beschreibbar, sondern dem objektiven Zufall unterworfen. Man erhält für c mal diesen Wert, mal jenen. Grund ist ja, dass der Zustand mit der be-stimmten Eigenschaft a un-be-stimmt ist bzgl. der Messgröße C: Die Eigenschaft, die zur Messgröße C gehört, besitzt das System nicht, wenn es die Eigenschaften bzgl. der Messgrößen A und B hat. (Siehe Grundfaktum Ia: Nichtexistenz aller klassisch denkbaren Eigenschaften gleichzeitig) Es gibt keine allgemein anerkannte Theorie des Messprozesses, die etwa beschreiben könnte, weshalb bei der Messung von C ein bestimmter Messwert c eintritt. Das erscheint aber auch nicht besonders bedauerlich, da ja - wie wir uns gerade überlegt haben - die zugehörige Eigenschaft vor einer Messung gar nicht realisiert ist. Diese ist etwas, was dann nur in den Hirnen der Betrachter oder Physiker existiert. Mit Hilfe der Messinstrumente werden Fragen an die Natur gestellt - im Sinne von klassischen Fragen nach klassischen Eigenschaften des Systems, etwa in dem Sinn "Elektron, welche Geschwindigkeit hast du?". Die Natur antwortet darauf in jedem Fall, auch, wenn es in einem Zustand ist, in dem es die Eigenschaft "Geschwindigkeit" nicht hat. Aber, da die Frage der Natur in diesem Fall nicht ganz angemessen ist, antwortet sie mal mit diesem Ergebnis, mal mit jenem. ("Auf eine dumme Frage kommt auch eine dumme Antwort.") (Siehe Grundfaktum IVa: Alle makroskopisch sinnvollen Eigenschaften sind messbar ), (Siehe Grundfaktum Ib: Messbarkeit aller klassisch denkbaren Eigenschaften)
I.6.4 Was ist überhaupt ein Teilchen im Sinne der Quantentheorie? . . . .. . . . . . . . . I.6.4 Was ist überhaupt ein Teilchen im Sinne der Quantentheorie? . . . . . . . . . . . . . . . I.6.4 Was ist überhaupt ein Teilchen im Sinne der Quantentheorie? . . . . . . . . . . . . . I.6.4 Was ist überhaupt ein Teilchen im Sinne der Quantentheorie? . . . . . . . . . .	In der klassischen Physik ist das klar: Ein klassisches Teilchen ist ein meist kleines Objekt, das einen wohldefinierten Ort und eine wohldefinierte Geschwindigkeit (bzw. Impuls) hat, meist noch eine Reihe weiterer Eigenschaften. Das gilt für idealisierte Punktteilchen wie auch für den gedachten Mittelpunkt eines ausgedehnten Teilchens.  Wir haben gesehen, dass es in der Quantenphysik keine solchen Objekte gibt, die zu irgendeinem Zeitpunkt gleichzeitig Ort und Geschwindigkeit besitzen. "Keine Geschwindigkeit" heißt dabei nicht, dass das Teilchen ruht. Es heißt, dass es die Eigenschaften "be-stimmte Geschwindigkeit" nicht gleichzeitig mit der Eigenschaft "be-stimmter Ort" besitzt, dass die Eigenschaft "be-stimmte Geschwindigkeit" physikalisch sinnlos ist, wenn gerade die Eigenschaft "be-stimmter Ort" festgestellt wurde und umgekehrt. Die Quantentheorie nennt die einzige bewährte Möglichkeit, in der Quantenphysik ein Teilchen zu definieren, nämlich: Gegenstand der Quantenphysik sind Quantenobjekte. "Teilchen sind Quantenobjekte, die abzählbar sind". Wenn wir von irgendeinem System ermitteln können, ob 1, 2, 3, ...  Stück von einem Objekt vorhanden sind, sprechen wir von Teilchen (im Sinne der Quantenphysik). Da Elektronen, Photonen, Atome, Protonen, ...   abzählbar sind, sind sie mit Sicherheit Teilchen, aber eben keine klassischen Teilchen. Um das zu betonen werden sie oft Mikroobjekte oder Quantenobjekte genannt, wobei Quantenobjekt eigentlich ein Oberbegriff zu Quantenteilchen oder Zwillingen etc. ist. Teilchen in diesem Sinn sind Träger einiger unveränderlicher Eigenschaften wie Masse (Ruhemasse, die auch 0 sein kann), elektrische Ladung, Spin, ... Es gibt auch Quantenobjekte, bei denen eine Messung der Teilchenzahl genau 2 ergibt. Es handelt sich um Teilchenzwillinge, z.B. Photonenzwillinge, die auch Biphotonen heißen, oder Elektronenzwillinge (siehe Kap. I.6.5). Heutzutage wird mit verschränkten Zuständen von vielen Tausenden von Atomen experimentiert, die also ein einziges Quantenobjekt bilden. Es gibt aber auch Systeme, die nicht aus einer be-stimmten Zahl von Teilchen bestehen. Laserlicht oder ein Atomlaser sind Beispiele. Dabei liefert eine Messung der Anzahl der beteiligten Photonen bzw. Atome Poisson-verteilte, streuende Messwerte. Deshalb werden solche Systeme auch - allgemeiner - Quantensysteme genannt. Wodurch unterscheiden sich Mikroobjekte bzw. Quantensysteme von klassischen Teilchen? Wir zählen sie hier noch einmal auf: Quantensysteme haben eine bestimmte klassisch denkbare Eigenschaft ohne eine Messung i.A. nicht. Quantensysteme können nicht alle klassisch denkbaren Eigenschaften gleichzeitig haben. Nach Messungen haben sie eine Reihe von be-stimmten Eigenschaften. Dazu komplementäre klassisch denkbare Eigenschaften haben sie dann nicht. Diese sind dann un-be-stimmt. Messungen un-be-stimmter Eigenschaften (also von Eigenschaften, die das Quantensystem jetzt nicht besitzt) sind möglich. Sie liefern objektiv zufällige Ergebnisse. Solche Messergebnisse treten gemäß einer objektiven Wahrscheinlichkeit gesetzmäßig ein. Durch eine Messung einer Messgröße A entsteht ein be-stimmter Messwert a. Eine Messung verändert also in der Regel den Zustand eines Quantensystems, sicher dann, wenn dieser die Messgröße A nicht als Eigenschaft hat. Wenn eine Quantensystem bzgl. einer Messgröße A in einem be-stimmten Zustand (Eigenzustand) ist, ist es gleichzeitig bzgl. einer dazu komplementären Messgröße C in einem un-be-stimmten Zustand. Eine Messung der Messgröße C liefert dann jeweils unterschiedliche Messwerte c, passend zu allen möglichen Eigenzuständen bzgl. der Messgröße C. Der be-stimmte Zustand bzgl. A lässt sich dann als Überlagerungszustand von allen möglichen Eigenzuständen bzgl. C ausdrücken. Im Eigenzustand bzgl. A sind dann alle klassisch denkbaren Möglichkeiten für den Ausgang von Messungen der Messgröße C enthalten. Mikroteilchen sind interferenzfähig. Interferenz findet statt, wenn verschiedene klassisch denkbare Möglichkeiten für den Eintritt eines Messergebnisses existieren, zwischen denen nicht unterschieden wird (z.B. Einteilchen-Interferenz). Quantensysteme mit gleichen be-stimmten Eigenschaften sind ununterscheidbar.   Demgegenüber gilt für klassische Teilchen: Sie haben alle klassisch denkbaren Eigenschaften, sogar gleichzeitig. Messungen ergeben bei genügender Messgenauigkeit stets nicht streuende Ergebnisse. Eine sorgfältig durchgeführte Messung verändert den Zustand eines Teilchens nicht (bzw. vernachlässigbar wenig). Bei bekannten Anfangsbedingungen entwickeln sich ihre Eigenschaften kausal mit der Zeit. Zukünftige Messergebnisse lassen sich in diesem Fall - wenigstens im Prinzip - eindeutig vorhersagen. Interferenz ist bei klassischen Teilchen ausgeschlossen. Klassische Teilchen mit gleichen Eigenschaften bzgl. ihres dynamischen Verhaltens sind unterscheidbar durch Eigenschaften, die belanglos für die Dynamik sind, z.B. durch eine Aufschrift. Hinweis: Wellen sind nicht abzählbar. Bei der Erklärung der Beugung von klassischen Wellen (z.B. Wasserwellen) durch die Überlagerung beliebig vieler Elementarwellen mittels des Huygensschen Prinzips wird das deutlich. In der Quantentheorie werden Teilchen allein durch die Abzählbarkeit definiert (Vornehm gesprochen: sie werden als "Eigenzustände des Teilchenzahloperators" definiert). Weil Teilchen abzählbar sind, ist es auch ihre elektrische Ladung (Vgl. Millikan-Versuch). Ebenso abzählbar ist die Masse bei Teilchen einer einheitlichen Sorte und die Energie, die sie transportieren, wenn sie alle die gleiche Energie haben, wie etwa die Photonen bei monochromatischem Licht. Ebenso, wie man nie eine halbe Elementarladung oder die halbe Masse eines Elektrons findet, findet man auch nie ein halbes Elektron oder halbes anderes Teilchen. Das gilt auch für komplexere Gebilde wie Atome oder gar Fulleren-Moleküle. Sie lassen sich zwar zerlegen und verraten dabei ihre innere Struktur, aber die "Spaltprodukte" sind dann etwas ganz anderes als die Ausgangsteilchen, also z.B. Elektronen, Protonen und Neutronen bei der Zerlegung eines Atoms. Atome, Fulleren-Moleküle, Bakterien, ... Menschen sind in diesem Sinn Teilchen, weil sie als Ganzes gezählt werden können. Es ist  für die Frage der Interferenz oder der Wegentscheidung bei einem Doppelspalt unerheblich, dass sie offenbar aus vielen Atomen und Elektronen zusammengesetzt sind. Genauso sind Protonen oder Neutronen in diesem Sinn Teilchen, obwohl man heute weiß, dass sie aus Quarks zusammengesetzt sind und damit eine komplexe innere und sogar räumliche Struktur besitzen. Bei sehr großen Systemen, schon bei großen Atomen und erst recht bei Menschen, zeigen aber Theorie und in Einzelfällen auch Experimente, dass sie durch die Ankopplung solcher Systeme an die Umgebung in kürzester Zeit aus einem un-be-stimmten Zustand in einen be-stimmten übergehen ("Dekohärenz"). Deshalb verhalten sich sehr große Systeme eher wie klassische (makroskopische) Teilchen, obwohl auch sie im Prinzip durch die Quantenphysik beschrieben werden. Zudem zeigt es sich, dass z.B. ein Doppelspalt-Versuch mit Menschen praktisch wegen der großen Masse und damit der winzig kleinen DeBroglie-Wellenlänge selbst bei geringsten messbaren Geschwindigkeiten nicht realisierbar ist.*) Licht und Materie können sich in Zuständen befinden ("können in Zuständen präpariert werden") mit einer be-stimmten Teilchenzahl (Fock-Zustände / "Teilchen-Zustände"). Solche Zustände werden auch benötigt bei Versuchen mit einzelnen Photonen, Elektronen oder Atomen. Eine solche Vorstellung ist recht naheliegend, besonders bei makroskopischen Gegenständen, die wir uns in der Regel aus einzelnen Teilchen (Atomen, Molekülen) zusammengesetzt denken, genauer: aus jeweils einer be-stimmten Zahl von Atomen, Molekülen, ... . Licht und Materie können aber auch in Zuständen mit un-be-stimmter Teilchenzahl sein. Misst man hier die Teilchenzahl, erhält man nach dem objektiven Zufall streuende Werte. Eine solche Vorstellung ist uns normalerweise fremd. Aber Laserlicht hat die größte Ähnlichkeit mit kohärentem klassischem Licht, wenn es sich in  so genannten kohärenten Zuständen mit un-be-stimmter Photonenzahl befindet. Wie einer der Nobelpreisträger von 2005, R.J. Glauber, schon 1963 herausfand, haben klassische elektromagnetische Wellen im dreidimensionalen Raum eine große Ähnlichkeit mit solchen Zuständen. Würde man die Zahl der beteiligten Photonen messen, würde man bei jeder (gleichartigen) Messung in der Regel zu völlig unterschiedlichen Ergebnissen kommen, eben weil in solchen Zuständen die Eigenschaft "be-stimmte Photonenzahl" nicht erfüllt ist. Die gemessenen Photonenzahlen (pro Zeiteinheit) entsprechen einer Poisson-Verteilung. Bei bestimmten "Bose-Einstein-Kondensaten" und bei Atomlasern, wo typischerweise 106 Atome einen gemeinsamen "BEC-Zustand" bilden, werden ebenfalls un-be-stimmte Teilchenzahlen diskutiert. Seit 2005 ist das auch experimentell nachgewiesen (Forschergruppen um Esslinger und um Westbrook). Die Atome müssen - um ein Bose-Einstein-Kondensat bilden zu können - so aus Nukleonen und Elektronen zusammengesetzt sein, dass sie ganzzahligen Spin haben, also Bosonen sind. Um es noch einmal ganz klar zu sagen: Elektronen, Photonen, Atome, Fulleren-Moleküle, Protonen, ... sind eindeutig Teilchen (im Sinne der Quantenphysik), aber keine klassischen Teilchen.  Aber nicht alles Licht und alle Materie liegt in Teilchen-Zuständen**)  vor. Insbesondere das Licht, das einer klassischen elektromagnetischen Welle am nächsten kommt, nämlich kohärente Strahlung eines Lasers, befindet sich nicht in Teilchen-Zuständen. *) Die geringe DeBroglie-Wellenlänge würde bei halbwegs guter Beobachtbarkeit auch Spaltabstände und Spaltbreiten in der Größenordnung der Wellenlänge notwendig machen. Dann müsste die Öffnung der Spalte sehr viel kleiner als eine typische Dimension eines Menschen sein. Beim erfolgreichen Doppelspalt-Versuch mit Fulleren-Molekülen von Zeilinger u.a. war der Moleküldurchmesser mit D =  1000 pm = 1 nm ebenfalls sehr viel größer als die DeBroglie-Wellenlänge l =  2.5 pm der Moleküle. Der Spaltmittenabstand betrug 100 nm bei einer  Spaltbreite von ca. 50 nm. **) mit bestimmter Teilchenzahl. Die Schrödinger-Gleichung ist nur zuständig für nichtrelativistische Systeme in Teilchenzuständen.
I.6.5 Testfall für das Verständnis der Quantenphysik: Zweiteilchen-Zustände Sie vertiefen die Vorstellung, dass Wellen(-funktionen) in der Quantenphysik keine realistischen Wellen und keine dreidimensionalen Wellen im Anschauungsraum sind, dass Teilchen in solchen Zuständen ohne Messung un-be-stimmte Eigenschaften und keine Individualität haben, dass die "Modellphilosophie" bei ihnen versagt. . . . .. . . .. . . I.6.5 Testfall für das Verständnis der Quantenphysik: Zweiteilchen-Zustände . . . .. . . . . . . . . . .	Die gesicherte Quantentheorie und auch einige Versuche mit Photonen lehren: Zwei oder mehr Teilchen können in so genannten " verschränkten Zuständen " erzeugt werden. Im Falle von zwei Elektronen oder Photonen spricht man von "Zweiteilchen-Zuständen" oder von Elektronen- bzw. Photonenzwillingen (Bezeichnung nach Zeilinger; man spricht auch z.B. von Diphotonen, andere von Biphotonen, wieder, damit sie nicht verwechselt werden mit Zuständen mit zwei einzelnen Photonen). Sie sind allein gekennzeichnet durch Eigenschaften des Gesamtzustands (z.B. Gesamtimpuls, Gesamtdrehimpuls, Gesamtenergie, ... ). Man darf sie sich nicht als zwei einzelne Teilchen ("Dreiklang des verschränkten Zustands") vorstellen. Verschränkte Zustände werden charakterisiert durch die (wenigen) Eigenschaften des Gesamtzustands, die "Geburtsurkunde des verschränkten Zustands", die häufig auf Erhaltungssätzen beruht. Audretsch spricht von einem "Stoff fast ohne Eigenschaften",  "ohne", weil der Gesamtzustand und die beitragenden Teilchen ohne eine Messung viele weiteren klassisch vorstellbaren Eigenschaften nicht haben, und "fast", weil ja die "Geburtsurkunde" einige wenige Eigenschaften festlegt. Als Oberbegriff zu quantenphysikalischen Teilchen, Teilchenzwillingen etc. verwendet man häufig den Begriff "Quantenobjekt". Auch Eigenschaften eines einzelnen Quantenobjekts können verschränkt sein, z.B. die Elektronen der Elektronenhülle eines Atoms oder Schwerpunkts- und Relativkoordinaten eines Atoms, auch der Kern eines Atoms und seine Elektronenhülle. Zweiteilchen-Zustände werden durch zwei in Koinzidenz geschaltete Detektoren nachgewiesen. Dann wird der Zweiteilchen-Zustand aufgebrochen. Jeder Detektor registriert ein Einzelteilchen, aber: Nur bei einer Koinzidenz, wenn also beide Detektoren gleichzeitig ansprechen, liefern sie ein Zählsignal und zeigen den Zweiteilchen-Zustand an. Für die Koinzidenzschaltung kann man sich eine UND-Schaltung vorstellen: Nur, wenn gleichzeitig Detektor 1 UND Detektor 2 anspricht, entsteht ein Ausgangssignal. Solche Zustände eröffnen einen weiten Bereich äußerst interessanter Anwendungen von der Quantenkryptographie zur Übertragung geheimer Nachrichten bis zum Quantencomputer, die noch Gegenstand der Forschung sind. Auch die Elektronen bereits eines He-Atoms (mit zwei Elektronen) befinden sich in einem verschränkten Zustand, hier also einem Zweiteilchen-Zustand, ganz entsprechend auch die Elektronen eines Mehrelektronen-Atoms. Solche Zustände kann man weder durch ein (naives) Wellenmodell noch durch ein Teilchenmodell anschaulich beschreiben. Hier versagt die "Modellphilosophie" ganz. Ein naives Wellenbild von Wellen in unserem 3-dimensionalen Anschauungsraum wird auch damit eindeutig widerlegt. Betrachten wir z.B. einen Zweielektronen-Zustand mit Gesamtimpuls 0 und Gesamtspin 0. Messungen der Teilchenzahl werden immer 2 ergeben. Misst man die Impulse beider Elektronen, wird man als Impulssumme immer 0 erhalten, d.h. die beiden Elektronen müssen immer mit gleichem Impulsbetrag in entgegengesetzten Richtungen nachgewiesen werden. Misst man die Spins beider Elektronen bzgl. einer beliebigen Orientierung, wird man immer finden, dass sie entgegengesetzt zueinander sind, um den Gesamtspin 0 zu ergeben. Aber, welchen Impuls jedes der beiden Elektronen nach einer Messung haben wird, ist zuvor völlig un-be-stimmt. Auch wird man bezüglich jeder beliebigen Richtung einen gleich gerichteten (und beim zweiten Elektron also entgegengesetzt gerichteten) Spin oder aber einen entgegengesetzten (und beim zweiten Elektron also gleich gerichteten) Spin beobachten. Ein Elektronen-Spin hat bzgl. jeder beliebigen Richtung nur zwei Einstellmöglichkeiten: gleichgerichtet parallel oder entgegegensetzt (antiparallel). So können wir auch hier sagen: Der Spin jedes der beiden Elektronen ist vor einer Messung völlig un-be-stimmt. Sie wissen: Verschränkte Zustände werden charakterisiert durch die (wenigen) Eigenschaften des Gesamtzustands, die "Geburtsurkunde des verschränkten Zustands", die häufig auf Erhaltungssätzen beruht. Man kann nachweisen, dass die beiden Elektronen nicht schon bei ihrer Entstehung (Vgl. "Bertlmanns Socke") be-stimmte Impulse und be-stimmte Spins haben, sondern dass die betreffenden Messwerte erst bei einer Messung von Eigenschaften eines einzelnen Teilchens entstehen, auch wenn die beiden Elektronen Lichtjahre voneinander entfernt sind. Deshalb spricht Audretsch von einem "Stoff fast ohne Eigenschaften". Z.B. könnte man ja - im Prinzip - erst nachdem sich die beiden Elektronen um Lichtjahre voneinander getrennt haben, entscheiden, bzgl. welcher Richtung der Spin gemessen werden soll. Das könnte keinen Einfluss mehr auf die Entstehung der beiden Elektronen haben. Vor einer Messung haben die beiden Teilchen in einem Zweiteilchen-Zustand keine be-stimmten Eigenschaften und damit auch keine Individualität; sie existieren dann nicht als konkrete Teilchen und sind nicht voneinander durch be-stimmte Eigenschaften unterscheidbar. Dafür passt keines der Modelle "Welle" oder "Teilchen". Teilchen entstehen bei einem solchen Zustand erst durch eine Messung; vorher haben sie keine Eigenschaften, die durch ein Teilchenmodell anschaulich beschrieben werden könnten. Aber nach einer Messung ist der Zweiteilchen-Zustand "aufgebrochen". Dann liegen wirklich zwei einzelne Teilchen vor, für die auch je ein Teilchenmodell - wie üblich - passen könnte. Wahrscheinlichkeiten für den Ausgang von Messungen an einem Zweiteilchen-Zustand können tatsächlich durch Wellen beschrieben werden. Aber das sind nach der gesicherten Theorie keine Wellen im dreidimensionalen Raum unserer Anschauung, sondern in einem abstrakteren mindestens 6-dimensionalen Raum (den wir uns sicher nicht mehr vorstellen können). Heisenberg nennt solche abstrakten Räume "Konfigurationsräume". Damit wird unmittelbar klar, dass es sich nicht um realistische Wellen handeln kann, sondern nur um abstrakte Wellen in einem solchen vieldimensionalen Raum, die allein die Aufgabe haben, Wahrscheinlichkeitsaussagen zu ermöglichen. Man darf sich einen Zwei-Teilchen-Zustand offenbar nicht als zwei einzelne Teilchen vorstellen. Es gibt in der klassischen Physik nichts Vergleichbares. Rückwärts muss man schließen, dass Entsprechendes auch für die "Wellen" bei Einteilchen-Zuständen gilt, auch wenn der Raum hier - man könnte sagen: zufällig  - auch 3-dimensional ist wie der Anschauungsraum: auch diese "Wellen" (-funktionen) gibt es nur in einem abstrakteren Raum als dem Anschauungsraum. Der abstrakte Raum ist dann bei Vernachlässigung des Spins ebenso dreidimensional wie der Anschauungsraum; diese Tatsache hat in der Vergangenheit leider für viel Verwirrung gesorgt, indem der abstraktere Raum der Quantentheorie fälschlich mit dem Anschauungsraum identifiziert wurde und die Vermutung entstand, dass z.B. ein Elektron zugleich ein Teilchen und eine Welle (im Anschauungsraum) sei. So versagt die "Modellphilosophie" hier ganz. Aber es wird auch ein Licht darauf geworfen, was die "Wellen" sogar bei Einteilchen-Zuständen bedeuten. Nach der Einsteinschen Relativitätstheorie ist es nicht möglich, dass sich nach einer Messung an Elektron 1 die Information "be-stimmter Spin des Elektrons 1" instantan (ohne Zeitverlust) auf das eventuell sehr weit entfernte Elektron 2 überträgt, damit dieses sich für seine Spinmessung rechtzeitig orientieren könnte. Die Folge einer Messung an Elektron 1 ist nicht die Ausbreitung einer Wirkung bis zum Elektron 2, sondern das Be-stimmt-Werden einer Kenntnis über das Elektron 1, aus der sich die Kenntnis über das Elektron 2 aus den Eigenschaften des Gesamtzustands automatisch ergibt. Deshalb sprechen manche Physiker von "Fernwirkungslosigkeit" bei verschränkten Zuständen. Allerdings, diese instantane Entstehung von Kenntnis ist eben auch nicht geeignet, Informationen mit Überlichtgeschwindigkeit zu übertragen und widerspricht damit eben nicht der RT.
I.6.6 Nachweis, dass auch bei Zweiteilchen-Zuständen die beiden Teilchen vor einer Messung keine individuelle Existenz und keine individuellen Eigenschaften haben  ("Bertlmanns Socke") (Siehe Grundfaktum V: Quantenmechanische Nichtlokalität bzw. "Fernwirkungslosigkeit")	Für den Nachweis (nach Zeilingers "Einsteins Schleier") wird eine Quelle für Elektronenzwillinge mit Gesamtimpuls und Gesamtspin 0 verwendet. Zeilinger geht vom Gegenteil der Behauptung aus, also von der Annahme, dass von der Quelle bereits verschiedenartige Elektronenpaare mit be-stimmten Spinorientierungen ausgesandt werden. Darunter könnte auch eines sein, dessen einer Spin parallel und dessen anderer antiparallel zur (beliebig gewählten) z-Richtung orientiert ist. Würde man jetzt eine Spin-Messung bzgl. der y-Richtung durchführen, würde man in 50% der Fälle bei jedem der beiden Elektronen einen Spin in y-Richtung und in 50% der Fälle einen Spin entgegengesetzt zur y-Richtung finden. Mit einer gewissen Wahrscheinlichkeit käme es dann auch vor, dass beide Spins parallel zur y-Richtung orientiert sind. Das widerspricht aber der Tatsache, dass der Gesamtspin des Elektronenzwillings 0 ist. Also ist die Annahme falsch. So, wie hier die Annahme von individuellen Elektronen mit be-stimmten Eigenschaften von der Quelle her zum Widerspruch führte und damit die Annahme widerlegte, ergibt sich auch in allgemeineren Fällen, dass die beiden Elektronen eines Elektronenzwillings von der Quelle her keine be-stimmten Eigenschaften mitbekommen. Bei Zweielektronen-Zuständen entstehen individuelle Elektronen mit be-stimmten Eigenschaften erst bei einer Messung an einem von ihnen. Dann wird der Zweielektronen-Zustand "aufgebrochen" in zwei Einelektronen-Zustände mit be-stimmten Eigenschaften. Ganz Entsprechendes gilt natürlich auch für Zweiphotonen-Zustände, bei denen man bislang mehrere experimentelle Bestätigungen (oder auch der Ostermeyer-Versuch) gefunden hat. Um den Sachverhalt griffig zu charakterisieren, spreche ich häufig vom "Dreiklang des verschränkten Zustands". Die Argumentation steht im Zusammenhang mit dem scheinbaren Einstein-Podolski-Rosen-Paradoxon (EPR-Paradoxon). Ein Doppelspalt-Versuch mit Zweiteilchen-Zuständen (Doppel-Doppelspalt-Versuch) bestätigt das Grundfaktum V (Quantenmechanische Nichtlokalität ) und zeigt ebenfalls, was für eigenartige, klassisch nicht vorstellbare Gebilde Elektronen- oder Photonenzwillinge, bzw. allgemeiner: Quantenobjekte in Mehrteilchen-Zuständen, sind.

.

.

( aktualisiert 2018 )