Von Ostermeyer et al. stammt ein Versuch (2009), bei dem ein Biphoton (Photonenzwilling) aus zwei Photonen gleicher Energie an einem Beugungsgitter Interferenz erzeugt. Da ein Echelette-Gitter verwendet wurde (blazed grating), trat außer der 0. Ordnung nur mehr die 1. Ordnung des Spektrums auf. Hier soll der Versuch als Prinzip-Versuch vereinfacht werden, indem ein Doppelspalt-Versuch diskutiert wird (vgl. auch Abouraddy et al.). Die Ergebnisse stimmen mit dem Original-Versuch im Prinzip überein.

Der Versuch zeigt u.a., dass sich Zweiteilchen-Zustände (wie Biphotonen oder Photonenzwillinge) anders verhalten als zwei einzelne Quantenteilchen.

Biphotonen (Photonenzwillinge) sind Quantenobjekte aus je zwei verschränkten Photonen, die aber ohne eine Messung keine individuellen Eigenschaften haben. Sie sind charakterisiert durch die Eigenschaften des Gesamtzustands, z.B. seinen Impuls, Drehimpuls bzw. seine Polarisation. Wäre der Gesamtimpuls eines Biphotons z.B. 0, wäre nach Messung des Impulses p von einem Einzelphoton, wenn also der Zweiteilchen-Zustand aufgebrochen ist in Einteilchen-Zustände, unmittelbar klar, dass dann der Impuls des so entstandenen zweiten Einzelphotons -p sein muss. Das regelt der Impuls-Erhaltungssatz. Mit Biphotonen können Experimente im Sinne des Einstein-Podolsky-Rosen-Paradoxons (EPR) gemacht werden. Solche Biphotonen-Zustände gibt es in der klassischen Physik überhaupt nicht. Sie lassen sich weder durch ein Teilchenmodell noch durch ein Wellenmodell (für Wellen im dreidimensionalen Anschauungsraum) korrekt beschreiben.

Biphotonen können z.B. mit einer Zweiphotonen-Quelle mittels parametrischer Fluoreszenz (parametric down conversion) erzeugt werden. Solche Biphotonen sind verschränkt bzgl. der Polarisation und des Impulses. Mit einem nachgeschalteten Mach-Zehnder-Interferometer können die Photonen eines Biphotons zeitlich und räumlich korreliert werden. D.h. sie verlassen die Lichtquelle gleichzeitig am gleichen Ort. Das wurde von Hong, Ou und Mandel realisiert. Diese Lichtquelle soll hier nach ihren Erfindern HOM genannt werden.

Im Ostermeyer-Experiment erzeugten also die Autoren  mit Hilfe vom geeignet justierten HOM - vereinfacht gesagt - einen räumlich korrelierten Biphotonen-"Strahl" (Die Detektoren bei HOM werden weggelassen. Einem Ausgang des Strahlteilers dort werden im Idealfall die Biphotonen entnommen). 

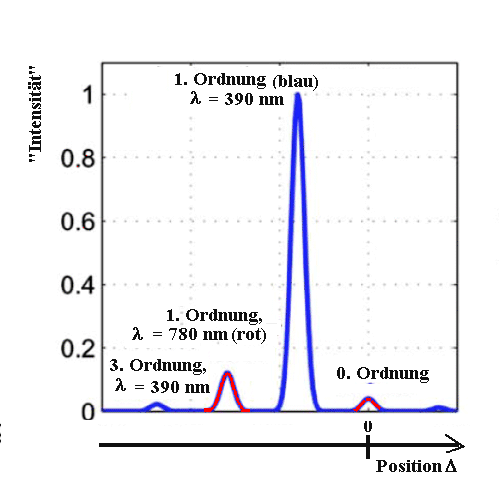Neben dem 0. Maximum war unter einem bestimmten Winkel ein Maximum 1. Ordnung zu beobachten, passend zu der Wellenlänge (bzw. Energie) der Einzelphotonen (λ = 780 nm, dunkelrot, auch in der Zeichnung links). Dort werden also gleichzeitig zwei einzelne Photonen der entsprechenden Energie nachgewiesen, in jedem Detektor eines. Bei idealer Justierung passiert das aber recht selten. Überraschenderweise traten aber noch Maxima 1. und 3. Ordnung in einer Entfernung Δ vom 0. Maximum auf, die zur halben Wellenlänge (λ = 390 nm, blau, auch in der Zeichnung) zu gehören schienen. Sie deuten auf ein Quantenobjekt mit doppelter Energie.

Das Einzelphotonen-Maximum (rot) ließ sich leicht erklären: Es kam von jeweils zwei Einzelphotonen, die bereits in der Lichtquelle oder unterwegs durch Aufbrechen des Zweiphotonen-Zustands entstanden waren. Zur Erklärung würde die übliche Doppelspalt-Theorie reichen.

Bei dem blauen Maximum (λ = 390 nm) handelt es sich aber um einen Effekt, der sich nur durch die speziellen Eigenschaften des Biphotonen-Zustands erklären lässt.

Solche Biphotonen-Zustände kommen in der klassischen Physik nicht vor. Es handelt sich um ein Quantenobjekt, an dem man immer die Teilchenzahl 2 misst, das aber  - ohne eine Messung - nicht aus 2 individuellen Teilchen besteht. Es wird in der Quantentheorie durch Wellenfunktionen  Ψ(x₁,x₂,t) in einem 6-dimensionalen Raum beschrieben. Es lassen sich Wahrscheinlichkeitsvorhersagen machen für Messergebnisse am ganzen Biphoton, aber auch für Messergebnisse an jedem der zwei Photonen, wenn der Zweiteilchen-Zustand aufgebrochen ist in Einzelteilchen-Zustände. Zur Angabe des Messorts x₁  bzw. x₂  für jedes Photon braucht man dann i.A. je drei Koordinaten, zusammen also 6.

Im Folgenden wird jetzt gezeigt, wie das Maximum 1. Ordnung für die blaue Linie zustande kommt, die nicht im Spektrum der Einzelphotonen enthalten ist, welche aus dem parametrischen Konverter heraustreten.

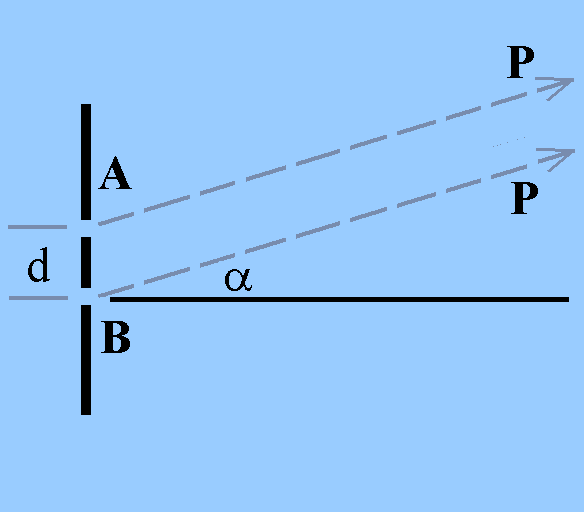Vereinfachend gehen wir aus von aus von einem parallelen "Strahl" von (räumlich korrelierten) Biphotonen, die senkrecht auf einen Doppelspalt auftreffen. Wie gesagt: Biphotonen bestehen nicht aus zwei individuellen Photonen, sondern sind besondere Quantenobjekte. Ein Biphoton (Photonenzwilling) wird beschrieben durch einen Zustand, bei dem man immer die Photonenzahl 2 messen würde, bei dem die beiden Photonen aber keine individuellen Eigenschaften haben. Wir argumentieren wie beim gewöhnlichen Doppelspalt-Versuch: Zwei "klassisch" denkbare Möglichkeiten für den Durchtritt des Biphotons durch den Doppelspalt sind naheliegend: durch Spalt A oder durch Spalt B*). Da zwischen ihnen im Experiment nicht entschieden wird, kommt es zur Interferenz.

Biphotonen (Photonenzwillinge) treten durch den Doppelspalt, aber ohne Messung nicht durch einen be-stimmten Spalt. Die gestrichelten Linien verbinden den Beobachtungspunkt P mit den Spalt- öffnungen. Sie stellen nur "klassisch denkbare" Pfade dar, i.A. keine tatsächlichen Wege der Biphotonen.

Hinter dem Doppelspalt in großer Entfernung wird die Eintrittsöffnung des Faserkopplers aufgestellt. Im Experiment möchten die Autoren sicher gehen, dass wirklich ein Zweiphotonen-Zustand mit räumlich und zeitlich korrelierten Photonen nachgewiesen wird, also teilen sie nach Durchtritt durch den Doppelspalt den an der Messstelle eintretenden Strahl mittels des Faserkopplers in zwei Teilstrahlen auf, die zu zwei Detektoren laufen. Sie registrieren einzelne Photonen. Aber durch den Strahlteiler ist gesichert, dass die Hälfte der Einzel-Photonen den Detektor 1 erreicht, die andere Hälfte den Detektor 2. Da die Photonen des Biphotons gleichzeitig auf den Strahlteiler treffen, werden sie mit großer Wahrscheinlichkeit in Koinzidenz gemessen, d.h. beide Zähler sprechen gleichzeitig an. Nur solche Ereignisse werden als Biphotonen-Ereignisse registriert.

Das merkwürdige Ergebnis ist, dass man neben dem naiv erwarteten Maximum 1. Ordnung für die Wellenlänge der beiden Einzelphotonen (λ = 780 nm) auch ein Maximum 1. Ordnung für die halbe Wellenlänge (λ = 390 nm) erhält. Dieses Ergebnis lässt sich nur erklären, wenn man akzeptiert, dass das zugehörige Biphoton nicht aus zwei individuellen Einzelphotonen besteht, sondern ein einheitliches Ganzes bildet, das ungeteilt irgendwie den Doppelspalt durchläuft.

.

Wenn Sie sich für den Nachweis interessieren, sollten Sie im Anhang nachlesen.

.

Es ist also so, als würden beide Photonen des Biphotons den klassisch denkbaren Pfad jeweils durch die gleiche Spaltöffnung wählen. Die Biphotonen haben als Ganze einen nur "klassisch" denkbaren Weg durch den einen oder den anderen Spalt. Sie treten als Ganze am Messpunkt ein und liefern dort gleichzeitig die Energie und den Impuls zweier Einzelphotonen ab. Das passt erfreulich zur halben Wellenlänge, wie das deBroglie mit λ = h/p vorausgesagt hätte. Davon hätten wir aber nicht von vornherein ausgehen können. Aber Vorsicht: Ohne eine Messung ist es sinnlos, von einem Weg der beiden Einzelphotonen zu sprechen, wir sagen: Ohne eine Messung gibt es keinen Weg der Einzelphotonen durch den Doppelspalt.

Die scheinbare Wellenlängenhalbierung lässt sich mit Einteilchen-Interferenz nicht erklären. Das gelingt nur mit Biphotonen, die auch Photonenzwillinge oder verschränkte Photonen heißen.

Wie man diesem Text hier unschwer entnehmen kann, bin ich allerdings nicht mit allen Aussagen von Herrn Rode einverstanden.

M. Ostermeyer, D. Puhlmann, and D. Korn, "Quantum diffraction of biphotons at a blazed grating", http://arxiv.org/ftp/arxiv/papers/0903/0903.2756.pdf

M. Ostermeyer, D. Puhlmann, and D. Korn, "Quantum diffraction of biphotons at a blazed grating", J. Opt. Soc. Am. B,  Vol. 26, No. 12, 2347 (2009)

C. K. Hong, Z. Y. Ou, and L. Mandel, "Measurement of subpicosecond time intervals between two photons by interference", Phys. Rev. Lett. 59, 2044 (1987)

K.Mattle, H. Weinfurter, P. G. Kwiat, and A. Zeilinger, “Dense coding in experimental quantum communication,” Phys. Rev. Lett. 76, 4656 (1996).

A.F. Abouraddy, B.E:A. Saleh, A.V. Sergienko and M.C.Teich, Double-slit interference of biphotons generated in spontaneous parametric downconversion from a thick crystal, J. Opt. B: Quantum Semiclass. Opt. 3, 50 - 54 (2001)

Anhang:

1. Der Nachweis gelingt (vereinfacht) folgendermaßen: Die Verbindungsstrecken zwischen den beiden Spalten und dem Messpunkt verlaufen quasi parallel. Die Ausbreitung von "deBroglie-Wellen" kann durch Wellenzahlvektoren k beschrieben werden, die unter anderem genau in diese Richtung zeigen. Um Messpunkte längs dieser Strecken anzugeben, braucht man also nur eine Koordinate, die wir x nennen. x₁ = x₂ = x seien Koordinaten längs dieser Achse beim Eintritt in den Zähler (genauer beim Eintritt in einen Wellenleiter, der zum Strahlteiler führt). Die Spalte haben die Koordinaten x_A und x_B. In klassischer Sprechweise ist also das eine Biphoton zum Interferenzpunkt die Strecke x - x_A gelaufen, das andere die Strecke x - x_B.

Es soll jetzt die Wahrscheinlichkeit berechnet werden, dass das Biphoton an der Stelle x nachgewiesen wird, also beide Photonen an dieser Stelle. Dazu ist das Betragsquadrat der Zweiphotonen-"Wellenfunktion" Ψ(x,x,t) zu berechnen. Die Wellenfunktionen der Einzelphotonen an den Spalten seien Ψ₁ und Ψ₂ sind (beides komplexwertige Zahlen, die auch einen zeitabhängigen Exponentialfaktor vom Betrag 1 enthalten). Bis zum gemeinsamen Messpunkt x verändern sie sich weiter (abgesehen vom zeitabhängigen Exponentialfaktor) gemäß Ψ₁ e^i(x-xA^)k    und  Ψ₂ e^i(x-xB^)k . Dann erhalten wir die Zweiteilchen-Wellenfunktion Ψ(x,x,t) am Messpunkt x mit dem Betrag des Wellenzahlvektors k = 2 · π/λ:

(A)    Ψ₁ e^i(x-xA^)·k · Ψ₂ e^i(x-xA^)·k  für die klassisch denkbare Möglichkeit des Durchtritts beider Photonen durch Spalt A

(B)     Ψ₁ e^i(x-xB^)·k · Ψ₂ e^i(x-xB^)·k  für die klassisch denkbare Möglichkeit des Durchtritts beider Photonen durch Spalt B  

Gemäß der Regel: Interferenz, wenn zwischen zwei klassisch denkbaren Möglichkeiten nicht entschieden wird, ergibt sich insgesamt

Ψ(x,x,t) =  Ψ₁ · Ψ₂ e^2i(x-xA^)·k   +   Ψ₁ · Ψ₂ e^2i(x-xB^)·k 

Bei parallelem Einfall auf den Doppelspalt gilt  Ψ₁ =  Ψ₂  . Die "Ablenkung" sei gerade so, dass ein Gangunterschied zwischen den beiden denkbaren Pfaden von Δs entsteht:  und damit x - x_A = x - x_B - Δs, also

Ψ(x,x,t) =  Ψ₁ · Ψ₂ e^2i(x-xA)^·k  e^-iΔs·k  ( e^iΔs·k + e-^iΔs·k ) = 2 · Ψ₁ · Ψ₂ e^2i(x-xA^)·k · e^-iΔs·k  · cos (Δs·k)

Das Betragsquadrat  fallen die Exponentialfaktoren weg. Es verbleibt der Faktor cos²(Δs·k). Er ist maximal, wenn Δs·k = Δs · 2 · π/λ = n·π ist, also, wenn Δs = n · λ/2 (n = 0, 1, 2, ... ).

Hätte man Einteilchen-Interferenz auf die gleiche Weise berechnet, hätte sich ein Maximum bei Δs = n · λ ergeben, wobei jeweils  n = 0, 1, 2, ... ist.

Die Maxima der Biphotonen-Interferenz liegen also dort, wo Einteilchen-Interferenz zur halben Wellenlänge ihre Maxima hätte. Genau das zeigt das Experiment.

2. Man könnte auch glauben, dass  folgende Denkmöglichkeiten beitragen:

Photon 1 durch Spalt A und zugleich (UND) Photon 2 durch Spalt B oder auch Photon 1 durch Spalt B und zugleich (UND) Photon 2 durch Spalt A. Die entsprechenden Zweiteilchen-Wellenfunktionen sind dann

(a)    Ψ₁ e^i(x-xA^)·k · Ψ₂ e^i(x-xB^)·k  für die klassisch denkbare Möglichkeit  Photon 1 durch Spalt A und zugleich (UND) Photon 2 durch Spalt B

(b)     Ψ₁ e^i(x-xB^)·k · Ψ₂ e^i(x-xA^)·k  für die klassisch denkbare Möglichkeit  Photon 1 durch Spalt B und zugleich (UND) Photon 2 durch Spalt A

Beide Anteile sind identisch. Sie werden hier weggelassen, weil es durch sie offensichtlich nicht zur destruktiven Interferenz kommen kann. Wegen der starken räumlichen Korrelierung der Photonen nach Verlassen der HOM-Lichtquelle ist dies wohl erlaubt.