I.4.1 Genauere Analyse des Doppelspalt-Experiments . Messung des Durchtrittsorts um möglichst herauszufinden, warum ein bestimmtes Teilchen in einem bestimmten Maximum nachgewiesen wird, oder um einen Mechanismus zu erkennen, der Teilchen beim Doppelspalt in die Maxima lenkt. Welcher-Weg-Messung, z.B. beim Doppelspalt mit "Atombeleuchtung" . . . . . . . . I.4.1 Genauere Analyse des Doppelspalt-Experiments . . . . . . . . . . . . . . . I.4.1 Genauere Analyse des Doppelspalt-Experiments . . . . . . . . . . . . I.4.1 Genauere Analyse des Doppelspalt-Experiments . . . . . . . . . . . . I.4.1 Genauere Analyse des Doppelspalt-Experiments . . . . . . . . . . . .	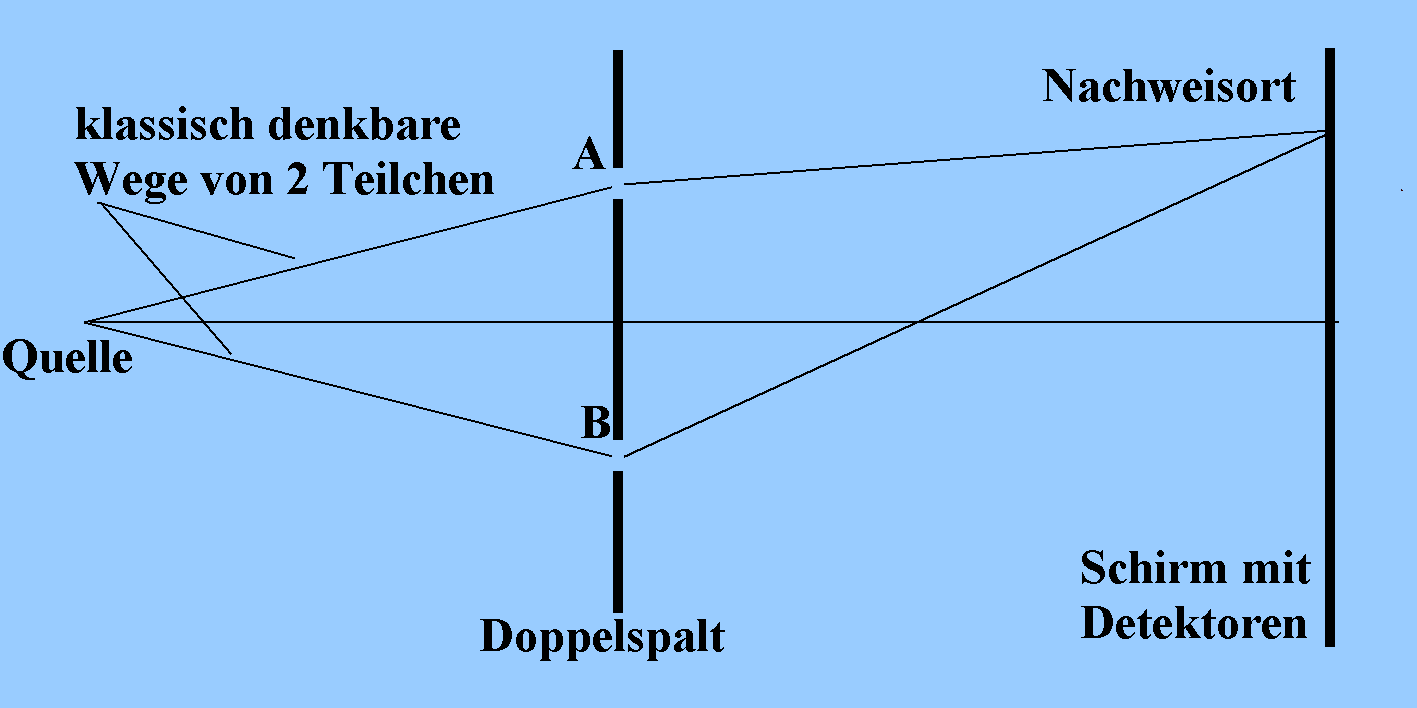Schema eines Doppelspalt-Versuchs. Beachten Sie: Hier sind keine Wege der Teilchen eingezeichnet, sonder nur "klasssisch denkbare Wege"! Wenn ein Teilchen bei einem Doppelspalt-Experiment auf dem Nachweisschirm registriert wurde, könnte es nach den Vorstellungen der klassischen Physik durch den Spalt A oder den Spalt B gelaufen sein. Man hat beim Doppelspalt offenbar zwei "nicht unterschiedene klassisch denkbare Möglichkeiten" des Durchtritts durch den Doppelspalt: entweder durch Spalt A oder durch Spalt B. Normalerweise wird experimentell nicht unterschieden, durch welchen der beiden Spalte das Teilchen hindurchtritt. Normalerweise wird nur die Interferenz auf dem Schirm betrachtet. Jetzt soll durch eine Messung unterschieden werden. Man ändert dazu den experimentellen Aufbau ab und installiert eine Vorrichtung, aus der man erkennen kann, ob das Teilchen durch Spalt A oder Spalt B gelaufen ist. Um quasi "Weg-Marken" an den Teilchen anzubringen,  gibt es verschiedene Möglichkeiten, wenigstens im Prinzip: (1) Wenn der Versuch mit Photonen gemacht werden soll, könnte man vor jede der Spaltöffnungen Polarisationsfilter mit zueinander senkrechten Polarisationen anbringen (Küblbeck). Das Photon, das durch Spalt A hindurchtritt, hat dann senkrechte Polarisation zu dem, das durch Spalt B hindurchtritt. (2) Wenn der Versuch mit Atomen oder Molekülen gemacht werden soll, könnte man, wenigstens in Gedanken, die durchtretenden Teilchen beleuchten, also mit Photonen bestrahlen ("Atombeleuchtung"). In simulierten Versuchen oder "Gedankenexperimenten" wird das auch mit Elektronen gemacht ("Elektronenbeleuchtung"). (3) Man könnte den Versuch mit hochangeregten Rydberg-Atomen durchführen, die in je einem Hohlraumresonator vor jedem Spalt beim Durchtritt Überschuss-Energie in Form eines Photons abgeben. Je nachdem, in welchem der beiden Hohlraumresonatoren man dann das Photon findet, weiß man, dass das Atom durch Spalt A oder Spalt B gelaufen ist. Alle diese Versuche haben ihre Tücken. Zu (1): Bringt man zusätzlich einen Analysator AN zwischen die Polarisatoren PO und den Schirm, der parallel zu einer der beiden Polarisationsrichtungen orientiert ist, sagen wir parallel zur Polarisation der Teilchen von Spalt A, dann kann man eindeutig sagen: Photonen, die jetzt auch noch den Analysator AN passieren, müssen durch Spalt A gekommen sein. Die Folge ist eine eindeutige "Welcher-Weg-Entscheidung". 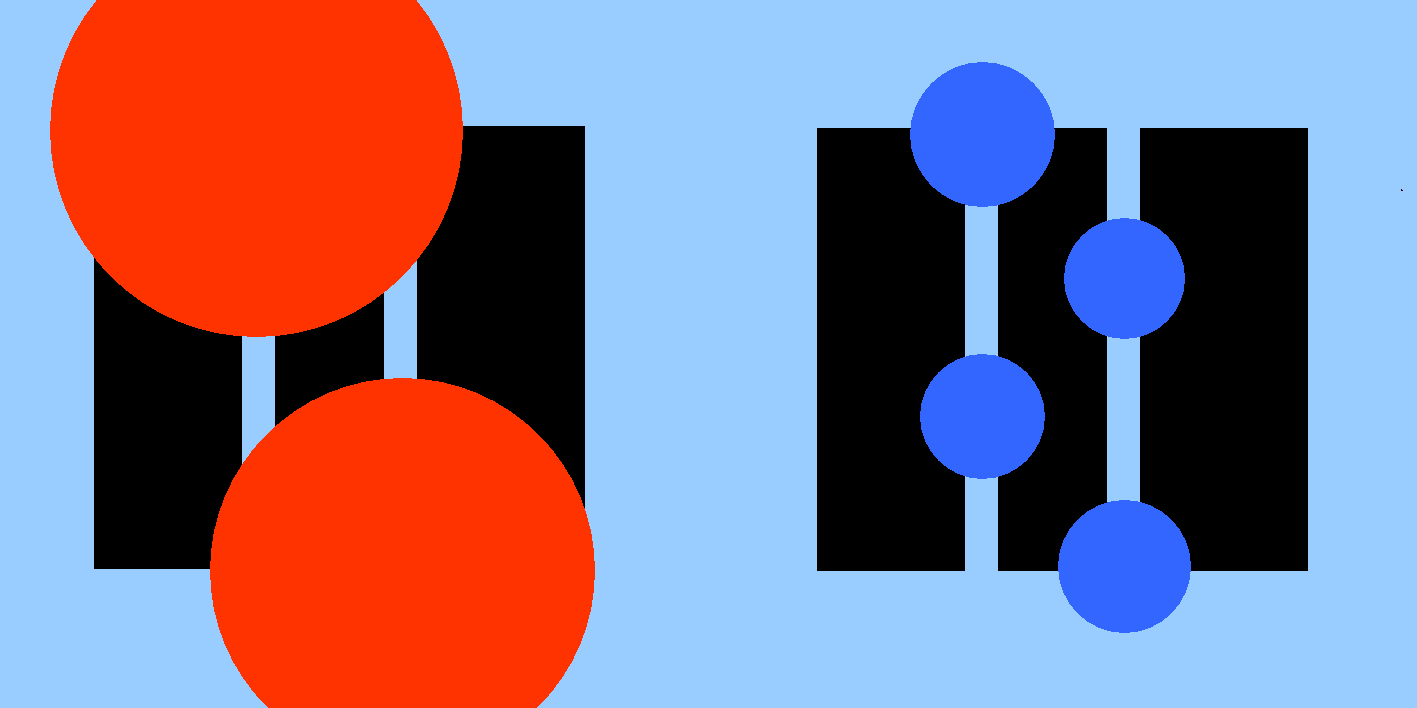Zu (2): Man könnte sich vorstellen, dass die Photonen an den durchtretenden Teilchen gestreut werden ("Atombeleuchtung"). Es bildet sich dann ein "Streuscheibchen" um das streuende Atom aus, mit einem Radius in der Größenordnung von der Wellenlänge des verwendeten Lichts. Bei geeignet langwelligem Licht (z.B. rotem) ist das Streuscheibchen so ausgedehnt, dass beide Spaltöffnungen überdeckt werden. Man kann dann an dem Streuscheibchen nicht erkennen, ob es in Spalt A oder Spalt B zentriert ist. Also wird man versuchen, die Wellenlänge möglichst klein zu machen, also z.B. mit blauem Licht. Dann könnte man im Prinzip eindeutig den Durchtrittsort des Teilchens entscheiden. Zu (3): Je nachdem, in welchem der beiden Hohlraumresonatoren man dann das Photon findet, weiß man, dass das Atom durch Spalt A oder Spalt B gelaufen ist. (4) Leichter kann man die Teilchen in einem Mach-Zehnder-Interferometer je nach dem durchlaufenen Weg markieren, im Prinzip aber entsprechend. Bei genügender Messgenauigkeit stellt man fest: Ein Durchtrittsort ist messbar. Welcher Durchtrittsort gemessen wird, ist eine Frage des objektiven Zufalls: einmal tritt das Teilchen durch den einen Spalt, ein andermal durch den anderen. der Detektor weist immer nur ein ungeteiltes Teilchen hinter einem der Spalte nach; niemals kann der Detektor den Durchtritt eines Teilchens durch beide Spalte gleichzeitig melden. Die erste Beobachtung, dass ein Durchtrittsort tatsächlich messbar ist, ist eine keineswegs selbstverständliche Besonderheit. Das werden Sie erst später einsehen. Es wird hier aber auch schon auf die noch allgemeinere Aussage hingewiesen, dass die Natur auf alle Fragen antwortet, die man in Form eines Experiments an sie stelllt, also auch nach dem Durchtrittsort. (Siehe Grundfaktum Ib: Messbarkeit aller klassisch denkbaren Eigenschaften) Die zweite und dritte Beobachtung entsprechen dem Ergebnis des Strahlteiler-Versuchs: Teilchen treten immer als ganze Teilchen auf, und zwar dem objektiven Zufall entsprechend. Daraus ergibt sich aber nach klassischen Vorstellungen ein Widerspruch: Eine Welle müsste durch beide Spalte gleichzeitig gehen um Interferenz zu erzeugen, Teilchen dagegen sind unteilbar und können - nach klassischer Vorstellung - nur durch einen Spalt treten. Um den Sachverhalt noch zu komplizieren: Bereits bei einem einzigen Teilchen beschreibt das Wellenbild die Wahrscheinlichkeitsverteilung für den Nachweis des Teilchens richtig. (Um Wahrscheinlichkeiten zu "messen" braucht man allerdings sehr viele solcher gleichartiger Experimente. Man muss dann immer wieder ein Teilchen im gleichen Zustand präparieren, z.B. mit gleicher mittlerer Geschwindigkeit v (und gleicher Geschwindigkeits-Un-be-stimmtheit Dv, etc.), und dann mit diesem Teilchen das Experiment durchführen.) Auch aus der Tatsache der beobachteten "objektiven Wahrscheinlichkeit" ergibt sich ein Grundfaktum der Quantenphysik, das hier nur erwähnt werden soll: Grundfaktum IIc: objektive Wahrscheinlichkeit. Objektiv heißt die Wahrscheinlichkeit, weil sie nicht auf einer subjektiven Unkenntnis des Physikers infolge Unfähigkeit oder einer unzulänglichen Physik beruht, sondern wesentlicher Teil aller Objekte der Quantenphysik ist. Sie lässt sich gesetzmäßig beschreiben. Es gibt ein weiteres Problem: Zwar ist Welcher-Weg-Information (WWI) möglich - auf die Frage nach dem Durchtrittsort reagiert ja die Natur mit einer eindeutigen Antwort  - , aber: die Welcher-Weg-Information zerstört die Doppelspalt-Interferenz: Sobald ein Durchtrittsort gemessen wird, verschwindet die Interferenzfigur; auf dem Bildschirm entsteht eine breite Verteilung der Teilchennachweise*), so als wäre jetzt ein Teilchenbild anwendbar. Also: Wenn zwischen den klassisch denkbaren Möglichkeiten nicht unterschieden wird (" nicht unterschiedene klassisch denkbare Möglichkeiten "), findet Interferenz statt. Sobald man aber zwischen den beiden klassisch denkbaren Möglichkeiten durch eine Messung unterscheidet, also den jeweiligen Durchtrittsort feststellt, verschwindet die Doppelspalt-Interferenz: Das Teilchen hat dann zwar einen wohlbekannten Durchtrittsort, aber man kann keinerlei kausale Verbindung vom Durchtrittsort zum Nachweis des Teilchens in einem bestimmten Punkt der früheren Interferenzfigur knüpfen. Beachten Sie auch: Zur Welcher-Weg-Entscheidung braucht man eine andere Apparatur als für die Beobachtung der Interferenz: kein Wunder, dass frühere Messergebnisse über die Interferenzfigur ihren Sinn verloren haben, wenn man den Durchtrittsort misst. Damit  ist ein scheinbares Paradoxon geklärt: Wenn einer der Spalte geschlossen ist, findet keine Doppelspalt-Interferenz statt, wohl aber, wenn beide geöffnet sind. Ein naiver Betrachter würde vermuten, dass ein Teilchen, das durch einen Spalt A tritt, sozusagen vorher erst "nachgeschaut" haben muss, ob der andere Spalt offen ist oder nicht. Das ist nicht vorstellbar. Der Fehler in der Überlegung ist klar: Hier werden zwei verschiedene Experimente miteinander vermengt. Das erste Experiment ist ein Experiment mit einer (drastischen) Ortsmessung. Sie sichert, dass das Teilchen nur durch Spalt A geht. Wir wissen längst, dass WWI die Interferenz ausschließt. Das zweite Experiment ist wirklich ein Doppelspalt-Interferenz-Experiment, das WWI - oder anders, einen be-stimmten Weg - ausschließt: Das durchtretende Teilchen hat keinen be-stimmten Weg durch die Spaltanordnung. Allgemeiner, und das wird in vielen anderen Versuchen bestätigt: Es lässt sich auf keine Weise eine Ursache dafür finden, dass ein bestimmtes Teilchen an einer bestimmten Stelle innerhalb der Interferenzfigur und nicht anderswo nachgewiesen wird, auch nicht im Zusammenhang mit dem Durchtritt durch einen bestimmten der beiden Spalte. Diese Beobachtung begründet die Ansicht, dass solche Kenntnis prinzipiell nicht gewonnen werden kann, dass hier "objektiv un-be-stimmte" Eigenschaften eine Rolle spielen, dass gesetzmäßige Aussagen nur mit "objektiver Wahrscheinlichkeit" gemacht werden können. (Siehe Grundfaktum Id: objektive Un-be-stimmtheit) (Siehe Grundfaktum IIc: objektive Wahrscheinlichkeit). Man kann niemals beides haben: einen eindeutigen Durchtrittsort ("WWI") und eine Interferenzfigur. Das bestätigt auch eine neue Deutung der Interferenz: Auch bei allen anderen Interferenz-Versuchen findet Interferenz immer dann und nur dann statt, wenn das beobachtete Ereignis auf verschiedenen klassisch denkbaren Möglichkeiten eintreten könnte, zwischen denen nicht unterschieden wird. (Interferenz-Bedingung) (Siehe Grundfaktum III: "Interferenz von Möglichkeiten") *) Die breite Verteilung ist allerdings von Minima unterbrochen, die dort liegen, wo die Interferenzfigur des Einfachspalts Minima hat. Weiter beobachtet man, dass auch bei Gewinnung der Welcher-Weg-Information bzgl. der beiden möglichen Durchtrittsorte die Einzelspalt-Interferenz bestehen bleibt: Die breite Verteilung nach Verschwinden der Doppelspalt-Interferenz ist  von Minima unterbrochen, die dort liegen, wo die Interferenzfigur des Einfachspalts Minima hat. Es sieht so aus, als bräuchte man doch beide "Bilder": Man kennt jetzt zwar den Einzelspalt, durch den das Teilchen durchtritt. Das sieht so aus, als würde man dafür das Teilchenbild verwenden können. Aber man beobachtet immer noch die Interferenzfigur des Einzelspalts mit breiteren Maxima und Minima. Der Grund für die verbliebene Anwendbarkeit des Wellenbilds ist hier, dass offenbar nicht durch eine Messung geklärt wurde, an welcher Stelle innerhalb des (jeweiligen) Einzelspalts das Teilchen durchtritt. Physiker, die es gewohnt sind, von "Wellen-" oder "Teilchencharakter" zu sprechen, müssten jetzt zugeben, dass in ein und demselben Versuch die Teilchen beide "Charaktere" zugleich zeigen müssten. Die hier vertretene Sprechweise erscheint demgegenüber einfacher. Auch hier unterscheidet man nicht durch eine Messung zwischen den beliebig vielen klassisch denkbaren Möglichkeiten des Durchtrittsorts innerhalb des jeweiligen Einzelspalt, also kommt es zur Interferenz (am Einfachspalt).
I.4.2 Welcher-Weg-Information und Interferenz sind komplementär zueinander . . Was ist Interferenz überhaupt? . . . . . . . . I.4.2 Welcher-Weg-Information und Interferenz sind komplementär zueinander . . Was ist Interferenz überhaupt? . . . . . . . . I.4.2 Welcher-Weg-Information und Interferenz sind komplementär zueinander . . Was ist Interferenz überhaupt? . . . . . .	Dass WWI die Interferenz zerstört, ist zunächst eine Erfahrungstatsache. Manchmal lässt sie sich auch kausal erklären, wenigstens, wenn man klassisch argumentieren möchte. Zu (1): Unterschiedlich polarisiertes Licht ist trotz gleichen Wellenlängen nicht interferenzfähig, weil die jetzt senkrechten elektrischen Vektoren der elektromagnetischen Welle sich nicht zu 0 ergänzen können. Zu (2): Bei der "Atombeleuchtung" übertragen die hochenergetischen Photonen bei kurzwelligem Licht auch viel Impuls in mechanischen Stößen an das streuende Teilchen. Durch diesen Impuls könnte - nach klassischer Vorstellung - das Atom "aus seiner Bahn geschleudert" werden. Das Atom wird daher "gestört" und man braucht sich nicht wundern, dass es sich anders verhält, als wenn nur die Interferenz beobachtet wird. Hochenergetische Photonen (z.B. blaues Licht) braucht man aber, um den Durchtrittsort genauer messen zu können; dann ist kaum Interferenz zu beobachten. Vermindert man die Störung durch niederenergetische Photonen (z.B. rotes Licht), kann man den Durchtrittsort nur ungenau entscheiden. Dann kann man immerhin noch eine "verwaschene" Interferenzfigur beobachten. Man kann wieder nicht beides haben: einen eindeutigen Durchtrittsort und eine geringe "Störung" der Atome. Ähnliche klassische Überlegungen haben historisch zu einer "Unschärferelation" geführt, die später behandelt wird. Sie sind aber sehr problematisch, weil man dabei annimmt, dass es ein "ungestörtes" "Verhalten" des Atoms und der Photonen gäbe. Zu (3): Das Verständnis, weshalb sich hier WWI und Interferenzfigur "beißen", ist komplizierter. Es hängt damit zusammen, dass Atom und Photon einen (verschränkten) Zwei-Teilchen-Zustand bilden. Nur die atomaren Anteile, nicht die photonischen könnten sich auf dem Schirm überlagern. Eine mechanische "Störung" wäre hier vernachlässigbar klein. Wir müssen uns hier aber vor Schwarz-Weiß-Malerei hüten: Misst man den Durchtrittsort durch den Doppelspalt nur ungenau,  (bei der "Atombeleuchtung" also z.B. mit dem energieärmeren gelben Licht), so ist die Interferenzfigur auch "verwaschen", aber noch erkennbar. Das kann auch durch simulierte Versuche am Doppelspalt oder im Mach-Zehnder-Interferometer veranschaulicht werden. Man hat bis heute kein Experiment gefunden, mit dem man Welcher-Weg-Information gewinnen könnte, ohne die Interferenz zu zerstören. Man hat auch kein Experiment gefunden, mit dem man ungefähre Welcher-Weg-Information gewinnen könnte, ohne die Interferenz zu schwächen. Man geht deshalb davon aus, dass das physikalisch unmöglich ist: Welcher-Weg-Information und Interferenz schließen sich immer gegenseitig aus. Welcher-Weg-Information und Interferenz sind also "komplementär" zueinander. Allgemein braucht man zur Messung komplementärer Messgrößen jeweils eine andere Apparatur: kein Wunder, dass die früheren Messergebnisse ihren Sinn verlieren. So liegt es also auch am Experimentator, welches Versuchsergebnis eintritt. Entschließt er sich dazu, eine Apparatur zu wählen, die ihm eine Welcher-Weg-Information liefert, dann verzichtet er automatisch auf  die Interferenzfähigkeit. Entschließt er sich aber, eine Apparatur einzusetzen, mit der er das Interferenzbild untersuchen kann, verzichtet er zwangsläufig darauf, Welcher-Weg-Information zu erhalten. Aber er kann sich auch entscheiden, nur ungefähre WWI zu erhalten, dann kann er immerhin ein verwaschenes Interferenzbild erwarten. (Der Einfluss des Experimentators wird deutlich bei einer "Herleitung" der Komplementarität aus der Heisenbergschen Un-be-stimmtheitsrelation nach Zeilinger). Die Konkurrrenz von WWI und Interferenz bestätigt die Auffassung der Interferenz als Ausdruck der "Konkurrenz von nicht unterschiedenen klassisch denkbaren Möglichkeiten". Interferenz hat in der Quantenphysik offenbar nichts damit zu tun, dass sich zwei realistisch vorzustellende Wellen überlagern, oder dass sich Teilchen irgendwie "zusammenlegen", sondern tritt dann auf, wenn es eine "Konkurrenz von nicht unterschiedenen klassisch denkbaren Möglichkeiten" gibt. (Siehe Grundfaktum III: "Interferenz von Möglichkeiten") Der Begriff "Welcher-Weg-Information" ist bei Betrachtung des quantenmechanischen Messprozesses nicht ganz unproblematisch. Eine etwas tiefer gehende Analyse finden Sie hier. Einstein-Vorschlag mit einer trickreichen Überlegung, leider nur im Sinne der klassischen Physik: Wenn ein Teilchen in einem seitlichen Maximum nachgewiesen wird, könnte dies als Folge eines seitlichen Zusatzimpulses py quer zur Ausbreitungsrichtung aufgefasst werden. Einstein versuchte, dafür eine klassische Erklärung zu geben, indem er annahm, dass - aus Impulserhaltungssgründen - der makroskopische Doppelspalt einen entgegengesetzt gleichen Rückstoß aufgenommen haben müsse, den man messen könne - wenigstens im Prinzip. Der Erklärungsversuch misslang aus folgendem Grund: Der Rückstoßimpuls auf den Doppelspalt würde dann dafür sorgen, dass sich der Doppelspalt in Querrichtung verschiebt, wobei die Interferenzfigur "mitgenommen" wird, gerade so, dass ein Maximum des verschobenen Spalts mit einem Minimum der früheren Interferenzfigur zusammenfallen könnte: die Interferenzfigur wird "ausgeschmiert", verschwindet. Viele andere solche "Gedankenexperimente" von Einstein und anderen Autoren (z.B. Feynman) lieferten immer wieder das gleiche Bild: Es ist nicht möglich, bei einer Interferenzanordnung einen Grund zu finden, weshalb ein Teilchen in diesem Maximum, ein anderes in jenem Maximum, ein drittes - wenn auch selten - in der Nähe eines Minimums nachzuweisen ist. Es ist deshalb mittlerweile verpönt, weil erfahrungsgemäß erfolglos, mit solchen klassischen Modellen, wie Einstein oder andere sie  erdachten, zu argumentieren. Alle solche Modelle benutzen klassisch denkbare Eigenschaften, die nicht zugleich existieren. Die Gedankenexperimente hatten dennoch einen unverzichtbaren Wert insofern an ihnen die Eigenheiten der Quantenphysik besonders klar herausgearbeitet werden konnten.
. . . . . . . . . . . . I.4.3 Folgerungen . . . . . . . . . . . .	(1) Auf alle klassisch denkbaren Fragen an ein Teilchen antwortet die Natur im Experiment mit eindeutigen Antworten.  Nach jeder klassisch denkbaren Eigenschaft lässt sich in einem Experiment fragen. (Siehe Grundfaktum IV: mögliche Messwerte und auch Grundfaktum Ib: Messbarkeit aller klassisch denkbaren Eigenschaften). Im Doppelspalt-Experiment konnte in getrennten Messungen die Häufigkeit eines Nachweises in der Interferenzfigur ebenso wie ein Durchtrittsort bestimmt werden. Aber auf unterschiedliche hintereinander gestellte Fragen (wie nach der Interferenz und dann nach dem Weg oder umgekehrt) erhalten wir in der Regel Antworten, die nicht zusammenpassen, die "komplementär" zueinander sind (Siehe Grundfaktum Ia: Nichtexistenz von Eigenschaften und Komplementarität). So ist die Frage nach den Eigenschaften oder dem Entstehen der Interferenzfigur "komplementär" zur Frage nach dem Durchtrittsort. (2) Es kann so prinzipiell nicht geklärt werden, warum ein Teilchen an dieser Stelle der Interferenzfigur oder an jener nachgewiesen werden kann. Die Physiker warfen u.a. deshalb ihre klassische Vorstellung über Bord, dass dies wie in der Makrophysik eine Ursache haben müsse, die vielleicht nur unbekannt ist. Nein, im Laufe der jahrzehntelangen Diskussion setzte sich die Mehrheitsüberzeugung durch: Das Teilchen hat - ohne eine Messung - keinen Weg von der Quelle zum Nachweisort, und es gibt keine physikalische Ursache dafür, dass das Teilchen gerade an einem bestimmten Ort der Interferenzfigur nachgewiesen wird. Damit ist gemeint: Es ist physikalisch sinnlos (kurz: sinnlos), von einem Weg des Teilchens von der Quelle zum Nachweisort auf dem Schirm zu sprechen. Ja, noch schärfer: Das Teilchen tritt erst auf, wenn wir es auf dem Schirm nachweisen. Vorher hat es keinen Sinn, ihm irgendein Verhalten oder irgendwelche Eigenschaften zuzuschreiben, es sei denn, diese werden in einem Experiment gemessen. Aber dann verschwindet die Interferenz. Der Quantenphysiker Zeilinger schrieb 1998: "Indeed, following Bohr, I would argue that we can understand quantum mechanics, if we realize that science is not describing how nature is but rather expresses what we can say about nature. This is where the current value of fundamental experiments such as teleportation lies: in helping us to reach a deeper understanding of our mysterious quantum world." Wie in diesem Versuch die Teilchen nicht gleichzeitig einen be-stimmten Durchtrittsort durch den Doppelspalt und Interferenzfähigkeit haben, so gilt auch ganz allgemein für Quantensysteme: Quantensysteme besitzen nicht alle klassisch denkbaren Eigenschaften gleichzeitig. Es gibt zueinander komplementäre Eigenschaften (Siehe Grundfaktum Ia: Nichtexistenz aller klassisch denkbaren Eigenschaften gleichzeitig). So hat das einfachste Quantensystem, ein Teilchen, nicht gleichzeitig einen be-stimmten Ort und eine be-stimmte Geschwindigkeit (dabei ist jeweils die gleiche Komponente bzgl. eines Koordinatensystems gemeint). (3) Deshalb nennt man die ganz zufälligen Nachweise der Teilchen in der Interferenzfigur einen Ausdruck des "objektiven Zufalls", weil er nicht von der subjektiven Kenntnis oder Unkenntnis der Physiker abhängt, sondern objektiv in der Natur vorhanden ist. Ähnlich sind die Physiker überzeugt, dass ebensowenig beim Aspect-Grangier-Experiment mit einzelnen Photonen am Strahlteiler je ein Grund gefunden werden kann, weshalb das eine Photon in Geradeaus-Richtung, ein anderes in Querrichtung nachzuweisen ist. Es handelt sich auch hier um "objektiven Zufall". (4) Der "objektive Zufall" tritt bei einem Experiment ein, wenn dabei eine Eigenschaft vermessen wird, die die Teilchen zugleich mit anderen, die sie wirklich haben, nicht besitzen (hier nämlich einen bestimmten Weg durch die experimentelle Anordnung). (5) Die Gesamtheit aller möglichen Meßwerte spiegelt dennoch objektive, d.h. vom Beobachter unabhängige, Eigenschaften des untersuchten Systems wieder, für die aber keines der Modelle 'Welle' oder 'Teilchen' voll angemessen ist. Ebenso wird die objektive Wahrscheinlichkeit für das Eintreten eines be-stimmten Messwerts gesetzmäßig beschrieben.
I.4.4 Die Komplementarität als Hilfsmittel für qualitative Überlegungen u.a. . . . . . . . . . . . . I.4.4 Die Komplementarität als Hilfsmittel für qualitative Überlegungen u.a. . . . . . . . . . . . .	1. Komplementarität als Hilfsmittel um auch komplexere Situationen in der Quantenphysik zu untersuchen Der Begriff der Komplementarität umfasst einerseits das Phänomen, dass ein Mikrosystem nicht gleichzeitig alle klassisch denkbaren Eigenschaften hat (1). Dieser Aspekt heißt - wie wir wissen - auch "Nicht-gleichzeitige-Messbarkeit". Wir haben Komplementarität mittlerweile verallgemeinert zur Erscheinung, dass auch nicht alle klassisch denkbaren Phänomene gleichzeitig auftreten können (2). So schlossen sich WWI und Interferenz gegenseitig aus. Beide Aspekte können genutzt werden, um qualitative Aussagen in der Quantenphysik zu machen. Beispielhafte Aussagen zu (1) als Folge der Komplementarität: Wenn eine Größe be-stimmt ist, muss die komplementäre Größe streuende Messwerte liefern, wie etwa ein Teilchen mit be-stimmtem Impuls, das völlig un-be-stimmten Ort hat. Wenn die z-Komponente des Elektronen-Spins be-stimmt ist, ist die x-Komponente un-be-stimmt. Später werden Sie kennenlernen: Wenn Licht mit be-stimmter Photonenzahl (oder auch Amplitude) untersucht wird, dann muss die Phase ganz un-be-stimmt sein. Dann kann man keine Interferenz erwarten. Beispielhafte Aussagen zu (2) als Folge der Komplementarität: Versuche am Doppelspalt und im MZI hatten den Aspekt (2) begründet. Überraschend ist auch folgendes Experiment: Auch mit 2 Lasern gleicher Wellenlänge und Polarisation lässt sich unter bestimmten Umständen Interferenz erzeugen. Das geht sogar dann, wenn die Intensität so gering ist, dass immer nur ein Photon im "Interferenzraum" ist, in dem sich die Strahlung beider Laser überlagert (Radloff 1971). Es ist schon überraschend genug, dass man offenbar nicht von jedem Laser mindestens ein Photon zur Interferenz braucht! Man kann von dem einen Photon, das so Interferenz zeigt, i.A. auch nicht feststellen, von welchem Laser es kam. Würde man den Weg des Photons bis zu seiner Quelle durch eine Messung zurückverfolgen, würde die Interferenz verschwinden, so zeigt dies das Experiment, und die Komplementarität bestätigt es. Es lassen sich mit der Komplementarität in diesem Sinn weiter auch Versuche einfach erklären, die von der Theorie her verschränkte Zustände erfordern würden, die anschaulich nicht mehr erfassbar sind: Interferenz mit 2 Lasern gleicher Wellenlänge: Der Versuch mit einem Photon im Interferenzraum lässt sich auch als Beispiel für verschränkte Zustände auffassen. Der verschränkte Zustand setzt sich folgendermaßen aus Einzelzuständen zusammen: [(kein Photon von Laser 1) und zugleich (ein Photon von Laser 2)] oder [(ein Photon von Laser 1) und zugleich (kein Photon von Laser 2)]. Wie in anderen verschränkten Zuständen besitzen Einzelteilchen ohne eine Messung keine individuelle Existenz - es hat keinen Sinn zu fragen, woher das Photon kommt. Tut man es trotzdem, so erhält man eine komplementäre Situation ohne Interferenz. Englert-Scully-Walther-Experiment : Wenn ein Photon den Weg des Atoms durch den Doppelspalt markiert, indem es in einem Resonator vor einer der beiden Spaltöffnungen zurückbleibt, wenn also WWI vorhanden ist, dann kann keine Interferenz entstehen. Mach-Zehnder-Interferometer mit verzögerter Entscheidung: Im Prinzip-Versuch  nach Zeilinger ist es evident, dass sich WWI und Interferenz ausschließen. Das Versuchsergebnis zeigt, dass es nicht daran liegen kann, dass das Teilchen schon beim ersten Strahlteiler entschieden hätte, ob es den einen der beiden Wege gehen möchte, oder den Weg offen lassen möchte. Die Entscheidung könnte sozusagen erst fallen, wenn das Teilchen sich schon entschieden haben müsste. Ähnlich bei den folgenden Versuchen: Mach-Zehnder-Interferometer mit verzögerter Entscheidung (nach Wheeler): Doppel-Doppelspalt-Versuch realisiert als Malvern-Experiment bei allen Versuche, bei denen Interferenz nur mit Koinzidenzzählern zu erhalten sind, z.B. Der Berkeley-Quantenauslöscher alle Quantenauslöscher wie das Mach-Zehnder-Interferometer als Quantenauslöscher Das Schöne bei diesem Verfahren der Komplementarität ist, dass man sich vielfach gar nicht die Mühe machen muss, mit den Methoden der Quantentheorie zu arbeiten. Vielfach genügt die pauschale Anwendung der Regel, dass sich WWI und Interferenz gegenseitig ausschließen. Man muss dann immer nur untersuchen, ob WWI möglich ist. Ähnlich kann man auffassen: 2.  Das Wellenmodell als teilweise erfolgreiches Hilfsmittel um Interferenz zu untersuchen Entsprechend hat es sich als zweckmäßig erwiesen, Interferenzversuche zunächst einmal mit dem Wellenmodell zu untersuchen. Das bewährt sich, insofern man dann die richtige Lage der Minima und Maxima findet. Die Untersuchung hat allerdings beschränkte Tragweite, weil Interferenz einzelner Teilchen, wie wir sie in der Quantenphysik beobachten, so eben nicht erklärt werden konnte. Mit der richtigen Quantentheorie lässt sich Interferenz vollständig untersuchen. Es soll hier noch eine weitere pauschale Methode erwähnt werden, die sich für qualitative Diskussionen eignet: 3. Die HUR als Hilfsmittel in der Quantenphysik Dazu erfahren Sie mehr in Kap. I.9.2. Bei allen drei Methoden handelt es sich nicht um "kausale" Erklärungen, die etwa den letzten Grund dafür angeben könnten, weshalb bestimmte Beobachtungen eintreten. Es handelt sich eher um "konsistente" Erklärungen, die zeigen, wie Beobachtungen sein müssen, wenn sie mit der Quantentheorie in Einklang sind, "konsistent" mit ihr sind.
I.4.5 Missverständliche Sprechweisen	Jetzt verstehen Sie, was viele Sprechweisen, die Sie in populärwissenschaftlichen Schriften oder Schulbüchern finden, eigentlich bedeuten. Beispiele finden Sie hier. Was man m.E. als Lehrer der Quantenphysik nicht tun sollte
I.4.6 Bestätigung mit Fulleren-Interferenzen "Charakter-Probleme"	Ein Fulleren-Molekül  ist ein sehr komplexes Gebilde aus 60 oder 70  in Sechserringen angeordneten Kohlenstoffatomen und ihren Elektronen. Zeilinger und seiner Gruppe ist es gelungen, mit Fulleren-Molekülen Doppelspalt-Interferenz bzw. Gitter-Beugung zu erzielen. Die Minima und Maxima hatten genau die Positionen, die man von einem Wellenmodell mit der korrekten DeBroglie-Wellenlänge her erwarten konnte. Ein Fulleren-Molekül kann nicht einerseits seinen komplexen Aufbau aus Kohlenstoff-Atomen und andererseits die einfache Struktur einer Welle haben, so dass sich also etwa die Materie zweier solcher Moleküle irgendwie "zusammenlegen" würden um sich gegenseitig auszulöschen oder zu verstärken. Nein, bei allen Teilchen wie Elektronen oder Fulleren-Moleküle haben Wellen eine tiefere Bedeutung (im Zusammenhang mit Wahrscheinlichkeiten), die nicht mit der Struktur irgendeiner Teilchensorte zusammenhängt. Heisenberg wies in seinem Buch "Der Teil und das Ganze" darauf hin, dass es sich bei den beobachteten Phänomenen nicht um eine spezielle Eigenschaft von irgendeinem Teilchen, sondern "aller Materie" handle, womit angedeutet ist, dass die Problematik von allgemeinerer, grundlegender Bedeutung ist und nichts mit den individuellen Eigenschaften eines bestimmten Objekts zu tun hat. Dort lehnt er es aus dem gleichen Grund auch ab, für Mikroteilchen einen speziellen Namen zu verwenden (z.B. "Wellikel" aus Welle und Partikel, oder "wavicle" aus wave und particle, wie aus den Anfangszeiten der Quantenphysik), mit dem versucht werden sollte, einem Teilchen die beiden Aspekte (Welle und Teilchen) zuzuordnen. Deshalb ist es sehr problematisch, von einem "Wellencharakter" oder einem "Teilchencharakter" zu sprechen, so als sei dies jeweils eine besondere Eigenschaft des betrachteten Quantensystems. Über die hier beschriebenen Grundzüge der Quantenphysik hinaus handelt es sich eher um die Weise, wie wir den Sachverhalt beschreiben oder sehen wollen, welche Frage wir in Form eines Experiments gestellt haben, und nicht, was das "Wesen" oder den "Charakter" oder die "Natur" der Quantensysteme ausmacht. Allerdings, das steht fest: Die Quantensysteme sind weder klassische Teilchen noch klassische Wellen und bestehen auch nicht aus solchen. Und für manche Quantensysteme, wie solche, die durch verschränkte Zustände (vgl. Kap. I.3.6) beschrieben werden, könnte man die Begriffe "Wellencharakter "oder "Teilchencharakter" ohne Umdeutung ohnehin nicht anwenden. Das lernen Sie in Kap. I.6.5  genauer kennen. Mittelstaedt (Philosophische Probleme der modernen Physik) hat es sinngemäß so formuliert: "Die Quantentheorie beschreibt die Natur wie sie sich zeigt, wenn sie mit realen Messgeräten vermessen wird." Wie sie "ist", bleibt dabei völlig offen.