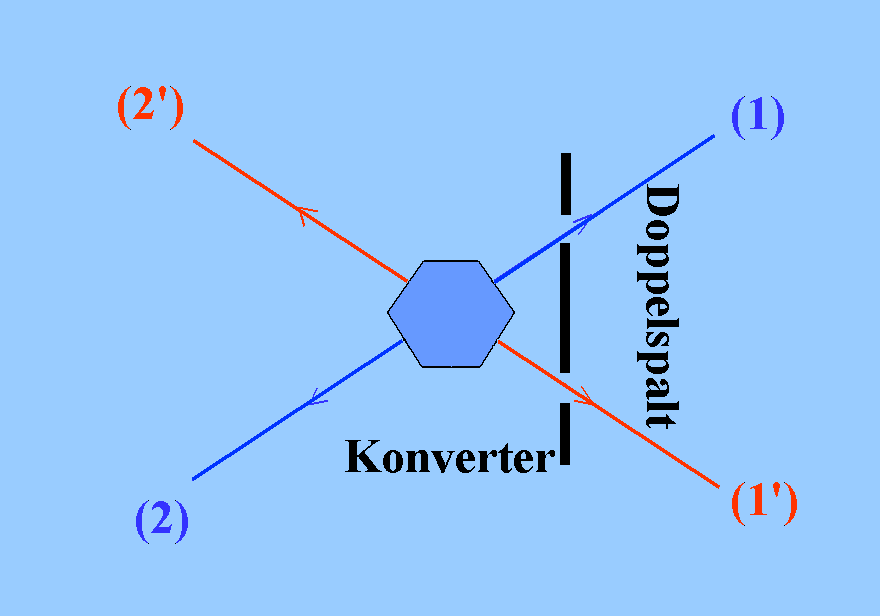
(1) Doppelspalt: Identische, gleichzeitig ausgesandte, aber richtungsverschiedene Photonen treffen auf einen Doppelspalt (rechts). Die Photonen stammen von nacheinander (in evtl. langen Zeitabständen) ausgesandten Photonenzwillingen, nämlich  z.B. (1') und (2') bzw. (1) und (2). Fragestellung: Was ist die Bedingung dafür, dass ein  Interferenzbild sichtbar ist? Lässt sich mit einem Teilchen (1) bzw. (1') Interferenz erzeugen, während mit dem Partner (2) bzw. (2') der Durchtrittsort bestimmt wird? Wenn das möglich wäre, hätte man gleichzeitig WWI (bzgl. des Durchtrittsorts) und Interferenz.

(2) Mindestvoraussetzung für die Interferenz ist eine kleine Quelle des Photonenzwillings: Wenn die Quelle (als solche könnte im Prinzip auch ein Kohärenzspalt fungieren) zu groß ist,  fallen etwa Minima von einem Quell-Punkt mit Maxima von anderen Quell-Punkten zusammen. Statt eines Hell-Dunkel-Musters würde man nur einheitliches Grau beobachten. Bei gleichen Abständen Quelle-Spalt und Schirm-Spalt muss die Quelle kleiner sein als der Abstand zweier Interferenzstreifen. Das nennt man die räumliche Kohärenzbedingung. Wenn räumliche Kohärenz (kleine Quelle) gegeben ist und das Photon (2) bzw. (2') "nicht beachtet" wird, erzeugt das Photon (1) bzw. (1') Interferenz. Sie läuft genauso ab, wie die normale Interferenz mit einzelnen Teilchen und heißt deshalb                                            "Ein-Teilchen-Interferenz" Die Argumentation erscheint suggestiv, ist sie aber mit Sicherheit richtig? Was heißt "nicht beachtet"?

(3) Vorüberlegungen am Einfachspalt, dessen Öffnung als Quelle für die Photonenzwillinge aufgefasst wird. In den Zeichnungen kann man sich die Verwendung eines ortsauflösenden Detektors (z.B. aus vielen Rechteckszellen) auf einem Schirm denken. Aus der Lage der ansprechenden Zelle soll auf die Richtung des einfallenden Photons geschlossen werden. 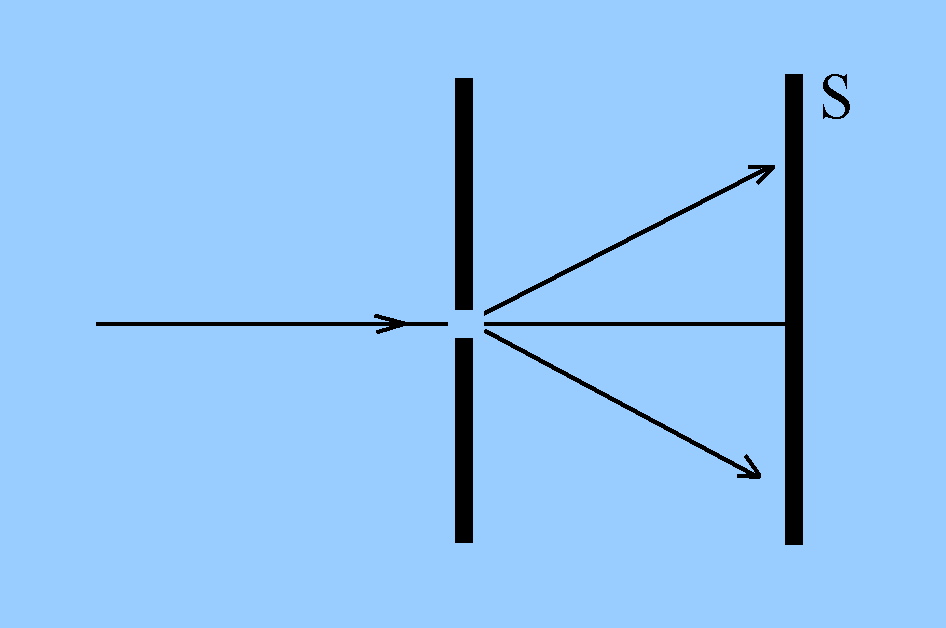Es soll versucht werden, aus dem Nachweisort auf dem Schirm S auf die Quer-Geschwindigkeit vor oder beim Spalt zu schließen. Dazu ist zu sagen: 1) Das kann nicht gehen, weil das Teilchen erst beim Nachweis Geschwindigkeit als Messwert erhält (objektive Un-be-stimmtheit). Das Teilchen besitzt diese Geschwindigkeit dann erst seit dem Nachweis auf dem Schirm. 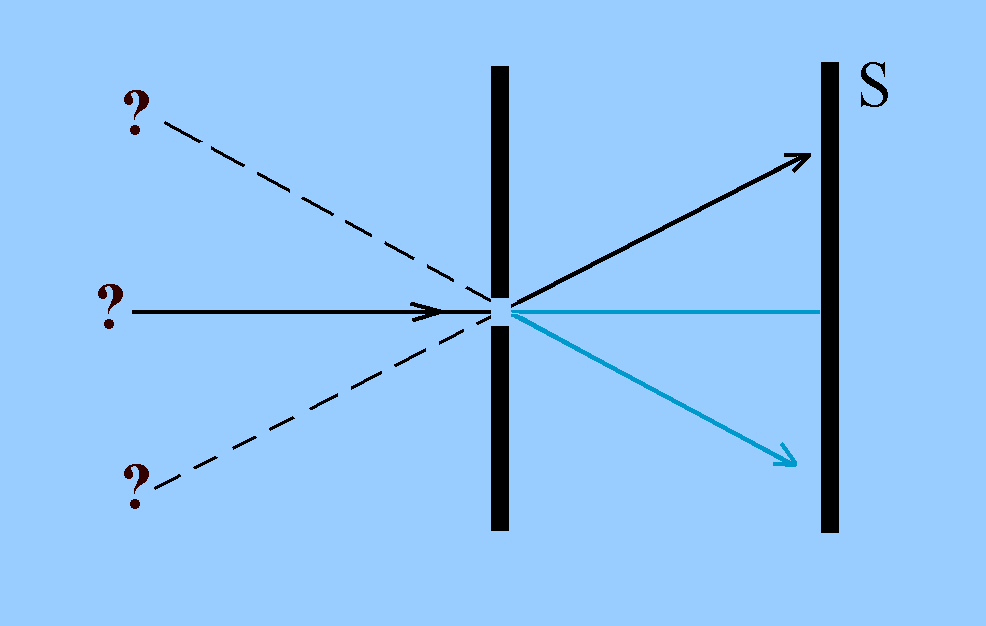2) Nach Registrierung eines Teilchens auf dem Schirm S ist nicht feststellbar, aus welcher Richtung vor dem Spalt es kam: Je enger die Spaltöffnung (Quelle), desto weniger genau wissen wir wegen der HUR, aus welcher Richtung das Teilchen gekommen ist; desto un-be-stimmter ist ja der Querimpuls. 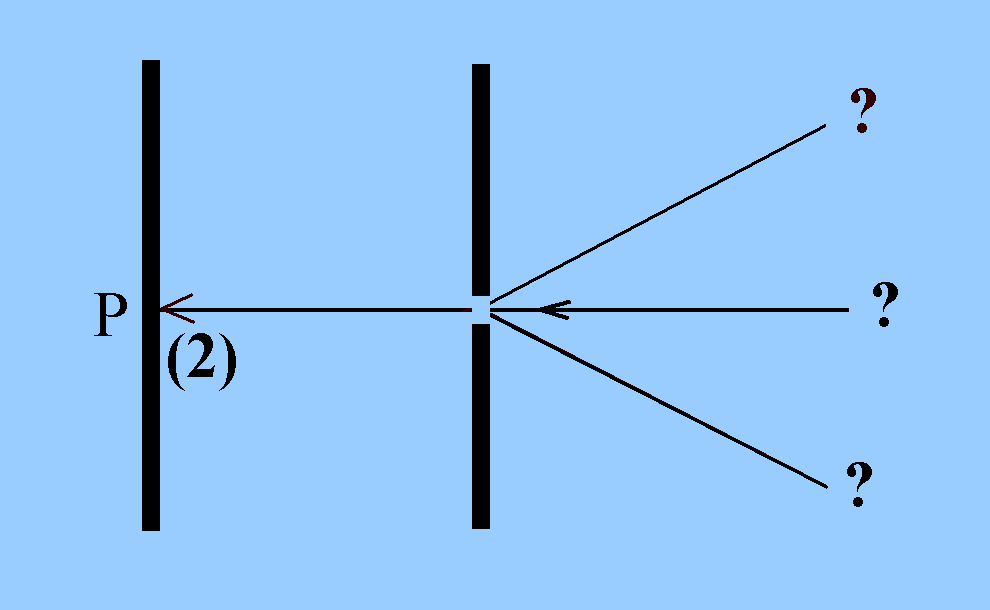3) Links soll jetzt ein fester Detektor stehen (Position P): Kann man feststellen, woher das nachgewiesene Photon 2 kommt? Wenn die Ortskoordinate durch die Größe der Quelle (des Einfachspalts) recht genau festgelegt ist, kann nach der HUR die Impulskomponente in gleiche Richtung nur ungenau festgelegt sein. Es ist also bei kleiner Quelle unklar, aus welcher Richtung die Teilchen in den Einfachspalt einfielen. Damit ist es nicht möglich, aus dem Ansprechen eines Detektors bei P auf die Richtung (Impulsrichtung) des einfallenden Teilchens zu schließen, wenn die Spaltöffnung/Quelle klein ist. Das soll noch einmal bildlich zusammengefasst werden: (A)  Bei kleiner Quelle kann zwar die Kohärenzbedingung erfüllt werden, aber der Querimpuls ist sehr un-be-stimmt und lässt keine Richtungsmessung zu (einer von vielen Detektoren kann ansprechen). 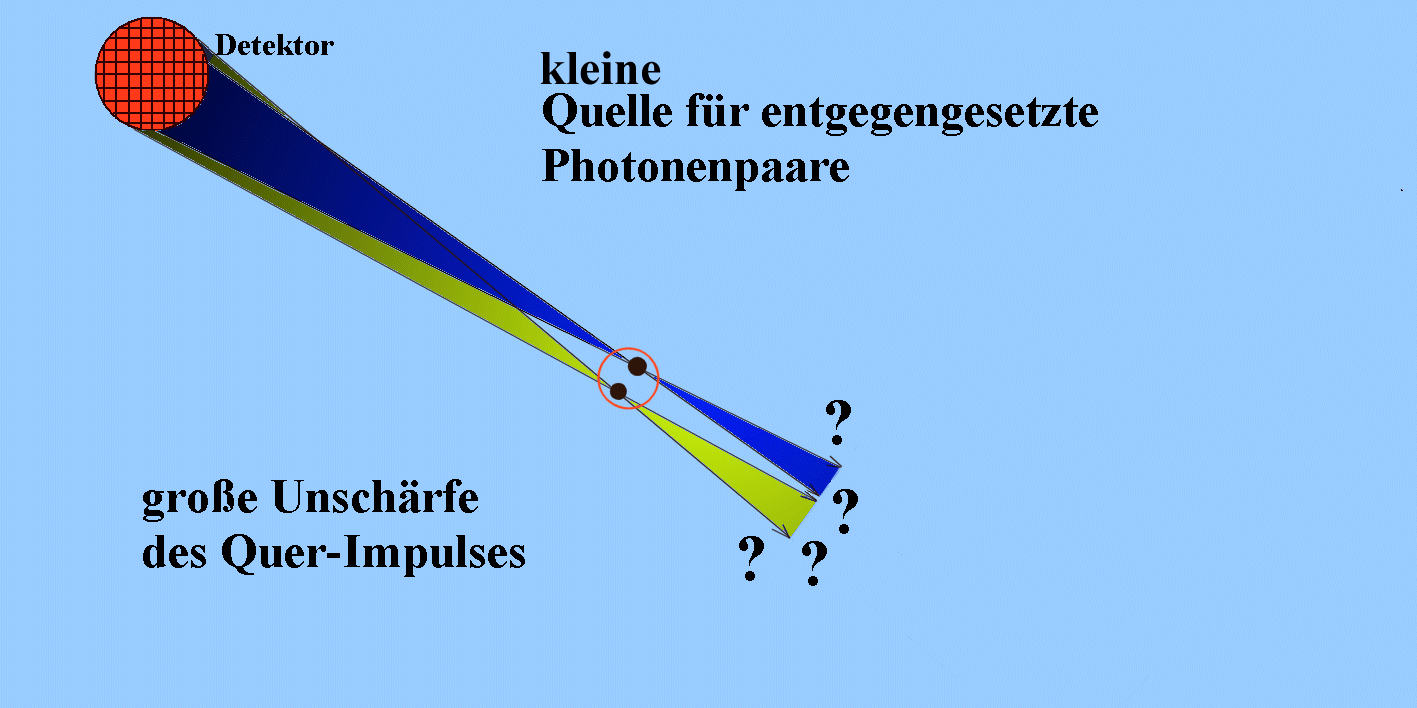(B) Bei ausgedehnter Quelle ist die Unschärfe des Querimpulses gering. Eine Richtungsmessung ist möglich, weil nur eine Zelle des Detektors von wenigen ansprechen kann.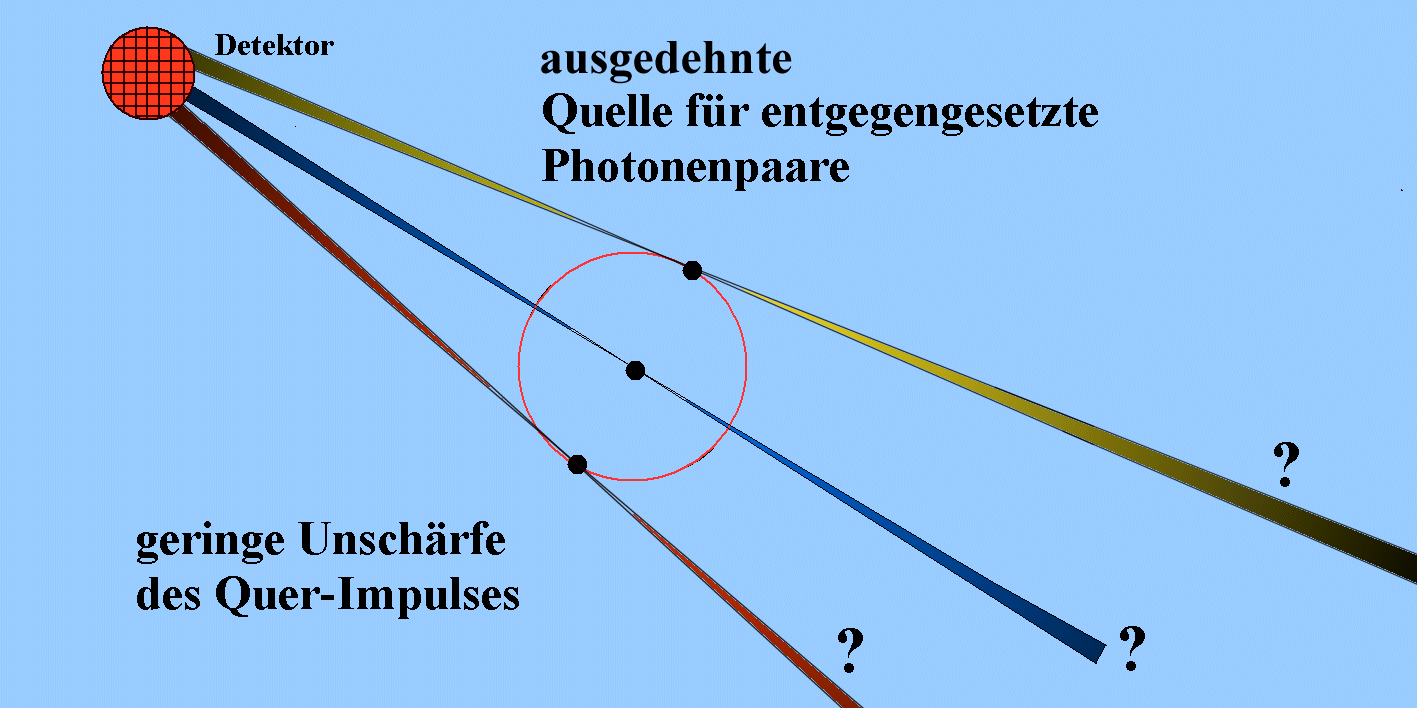

(4) Jetzt wieder Doppelspalt mit Quelle für Photonenzwillinge . Folgerung aus Abschnitt (3): Je kleiner die Quelle ist, desto ungenauer kann der Impuls von Teilchen 1 aus der Richtung geschlossen werden, unter der das Teilchen 2 registriert wurde. Je genauer der Impuls von Teilchen 1 aus dem Teilchen 2 bestimmt werden soll, desto größer muss die Quelle sein. a) Also: Wenn aus Registrierung von Teilchen 2 auf den Weg des Teilchens 1 durch einen der Spalte (über die Impulsrichtung) geschlossen werden soll, muss die Quelle eine Mindestgröße haben: Je kleiner die Quelle, umso weniger genau kann man durch Messung an Teilchen 2 darauf schließen, durch welchen Spalt Teilchen 1 gelaufen ist. b) Andererseits darf Quelle nicht zu groß sein, damit ein Interferenzbild beobachtbar ist (Bedingung: räumliche Kohärenz). Es gibt also eine kritische Größe der Quelle. Bei gleichen Abständen (links und rechts vom Doppelspalt) entspricht diese dem Abstand zweier Interferenzstreifen. Man kann wieder einmal nicht beides zugleich haben: ein klares Interferenzbild und Kenntnis über den Weg der Teilchen, die dieses Interferenzbild erzeugten. Damit ist die Komplementarität zwischen Interferenzbild und Weg des Teilchens aus der HUR für die Ausdehnung der Quelle hergeleitet. Zeilinger: "Zwei Größen sind dann komplementär zueinander, wenn die Informationen über beide nicht gleichzeitig vorhanden sein können." Der Experimentator muss sich durch die Anlage des Experiments entscheiden, welche der komplementären Größen er messen möchte. Hier tut er es durch die Auswahl der Quellengröße.

(5) Es ergibt sich also folgende Feststellung: große Quelle:  keine Interferenz, weil WWI möglich. kleine Quelle:  Ein-Teilchen-Interferenz, aber keine WWI möglich. Dabei ist es unerheblich, ob ein Detektor für Teilchen 2 aufgestellt ist. Allein, dass man diesen Weg bei großer Quelle bestimmen könnte, reicht aus, um die Interferenz zum Verschwinden zu bringen. Umgekehrt, wurde schon gesagt, dass Interferenz möglich ist, wenn die Teilchen (2) bzw. (2') "nicht beachtet" werden. Das heißt nach diesen Überlegungen konkret, dass es nicht möglich ist, aus den Teilchen (2) bzw. (2') auf den Durchtrittsort zu schließen. Das wird ausgeschlossen durch eine kleine Quelle. Zeilinger sinngemäß: "Keine Interferenz, wenn irgendwo auf der Welt Information über den Weg des Teilchens vorhanden ist."

Alternative Deutung: Zu (2): "Nicht beachtet" heißt "belanglos"; über die linken Anteile der Zwei-Teilchen-Wellenfunktion wird bei der Berechnung von Nachweiswahrscheinlichkeiten hinweg integriert,  so dass nur noch die überlappenden Anteile rechts Interferenz ermöglichen, wie bei der normalen Ein-Teilchen-Interferenz. Zu (4): Über die linken Anteile der Zwei-Teilchen-Wellenfunktion kann nicht hinweg integriert werden, also reichen rechte Anteile nicht zur Interferenz aus.