I.9.1 Klassische Analoga mit "Unschärfen"
Es muss im Folgenden klar werden, dass es sich bei den zunächst besprochenen klassischen Analoga, vorsichtig "Unschärfen von Messgrößen" genannt, um etwas grundsätzlich anderes als um die "Un-be-stimmtheiten" der Quantenphysik handelt:
Im klassischen Fall kommen "Unschärfen", wie Sie gleich sehen werden, durch eine Verteilung tatsächlich existierender Eigenschaften zustande, am klarsten als Schwankungsbereich, z.B. von Impuls- und Ortskoordinate bei einer Planetenbewegung. Dazu gehören aber auch Messungenauigkeiten ("Messfehler") oder ein Bereich der Unkenntnis über konkrete Werte, wie etwa bei Aussagen zur kinetischen Energie von Atomen in der Wärmelehre. Die betreffende Messgröße hat dabei sicher einen wohldefinierten Wert. Dieser ist nur nicht bekannt oder soll nicht angegeben werden.
Bei Un-be-stimmtheiten existieren dagegen die betreffenden Eigenschaften des Quantensystems ohne eine Messung nicht. Wenn eine Messung durchgeführt werden soll, muss man in diesem Fall objektiv zufällige Ergebnisse in einem gewissen Streu-Bereich erwarten.
Un-be-stimmtheit war bisher eine Erscheinung, nämlich die, dass eine Messgröße streuende Messwerte liefert, wenn sich das Mikrosystem in einem Zustand befindet, der die betreffende Messgröße nicht als Eigenschaft besitzt. Die folgenden Überlegungen führen schrittweise zum Begriff der "Un-be-stimmtheiten" als Maßgrößen. Wir betrachten dazu als Erstes ein verwandtes Beispiel, wo solche Un-be-stimmtheiten nicht vorkommen, einen Knall in der Akustik.
|
I.9.1.1 endlicher akustischer Knall
Prototyp für Zeit-Frequenz-Unschärfe .
. . . . . . . . . .
|
|
I.9.1.1 endlicher akustischer Knall
Prototyp für Zeit-Frequenz-Unschärfe . . . . . . . . . |
Bei der folgenden Zeit-Frequenz-Unschärfe sind bei einem Wellenzug bestimmter Dauer die durch die "Frequenzunschärfe" beschriebenen Frequenzanteile alle in der Überlagerung präsent und real.
Im Versuch 1 können Sie sich das Ergebnis erarbeiten: Akustische Analoga zur HUR_1
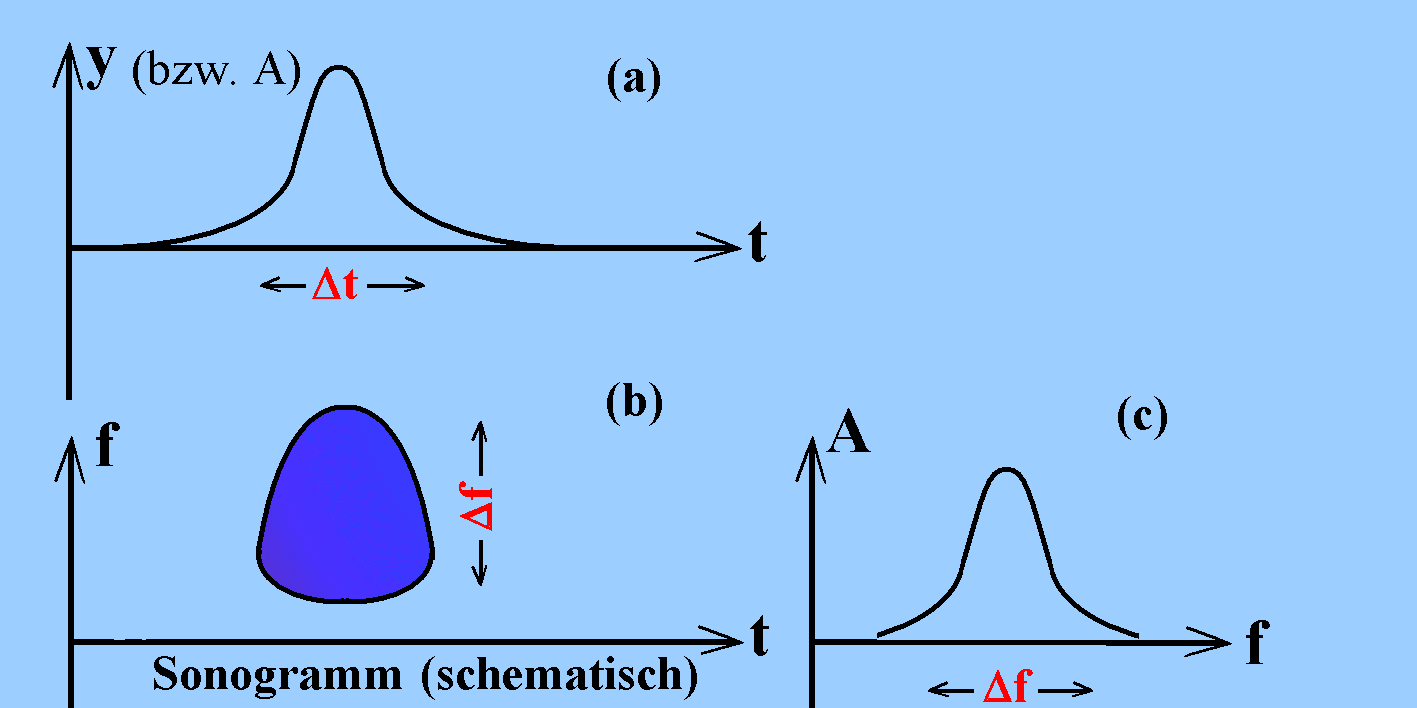 |
| Der Zeitverlauf eines Knalls ist in der Zeichnung (a) schematisch dargestellt; nennenswerte Auslenkungen hat er nur in einem bestimmten Zeitintervall der Breite Δt. Es kann sich ganz offensichtlich nicht um einen reinen Ton handeln. Im Unterschied dazu ist nämlich ein reiner (Sinus-)Ton "monochromatisch", besteht also aus einem einheitlichen Frequenzanteil mit der Frequenz f, und ist periodisch ohne zeitlichen Anfang und Ende. Stattdessen ist ein Knall (c) eine Überlagerung von beliebig vielen reinen Tönen mit benachbarten Frequenzen aus einem bestimmten Frequenzintervall Δf . Zur Darstellung der beiden Größen: Zeit t und Frequenz f dient ein so genanntes Sonogramm (Spektrogramm), das Sie mit bestimmten Programmen (z.B. GRAM) und der Soundkarte im PC leicht erstellen können. Seine schematische Form erkennen Sie in der oben stehenden Graphik (b). |
Nach dem Versuchsergebnis ist es plausibel (und es lässt sich auch beweisen), dass das Produkt aus Zeitdauer Δt und Frequenzbreite Δf konstant ist
|
|
Bei den Größen Auslenkung y und Amplitude A des Frequenzanteils, genauso wie bei Δt und Δf handelt es sich um rein klassische Größen. Für jeden Zeitpunkt könnte man Auslenkung y und und die beteiligten Frequenzen messen, wie es im Sonogramm gemacht wurde. Mit Quantenphysik hat dies überhaupt nichts zu tun.
Dennoch könnte man das Zeitintervall auch Zeit"unschärfe" und das Frequenzintervall Frequenz"unschärfe" nennen, also Größen, die die Abweichung von einem Zeitmittelwert und einem Frequenzmittelwert kennzeichnen. Dann könnte man bereits für diesen klassischen Fall sagen, dass das Produkt von Zeit- und Frequenz"unschärfe" konstant ist:
|
Große Zeit"unschärfe" Δt bedingt geringe Frequenz"unschärfe" Δf und umgekehrt. |
Versuch 2: Akustische Analoga zur HUR_2
Nehmen Sie wieder die einzelne Halbwelle des Sinus (ausgehend von einem 100 Hz-Sinus), wie oben erzeugt, und schneiden Sie diesmal, wieder mit einem Programm wie GOLDWAVE, höhere Frequenzen weg mit einem Tiefpass, den das Programm bereitstellt. Bei einer Abschneidefrequenz von z.B. 500 Hz entstehen aus dem einzelnen Knall gedämpfte Oszillationen, die einige Schwingungen lang anhalten. Je geringer Sie die Abschneidefrequenz wählen, desto länger anhaltend sind die Oszillationen. Oder anders, mit der jetzigen Sprechweise: Je geringer die Frequenzunschärfe Δf (des zugelassenen Bereichs), desto größer ist die Zeitunschärfe Δt des entstehenden Signals.
Wieder folgt:
|
Geringe Breite der Frequenzverteilung Δf bedingt große Zeitdauer Δt und umgekehrt. |
I.9.1.2 Ebenes klassisches Wellenpaket hinsichtlich Ort und Wellenlänge;
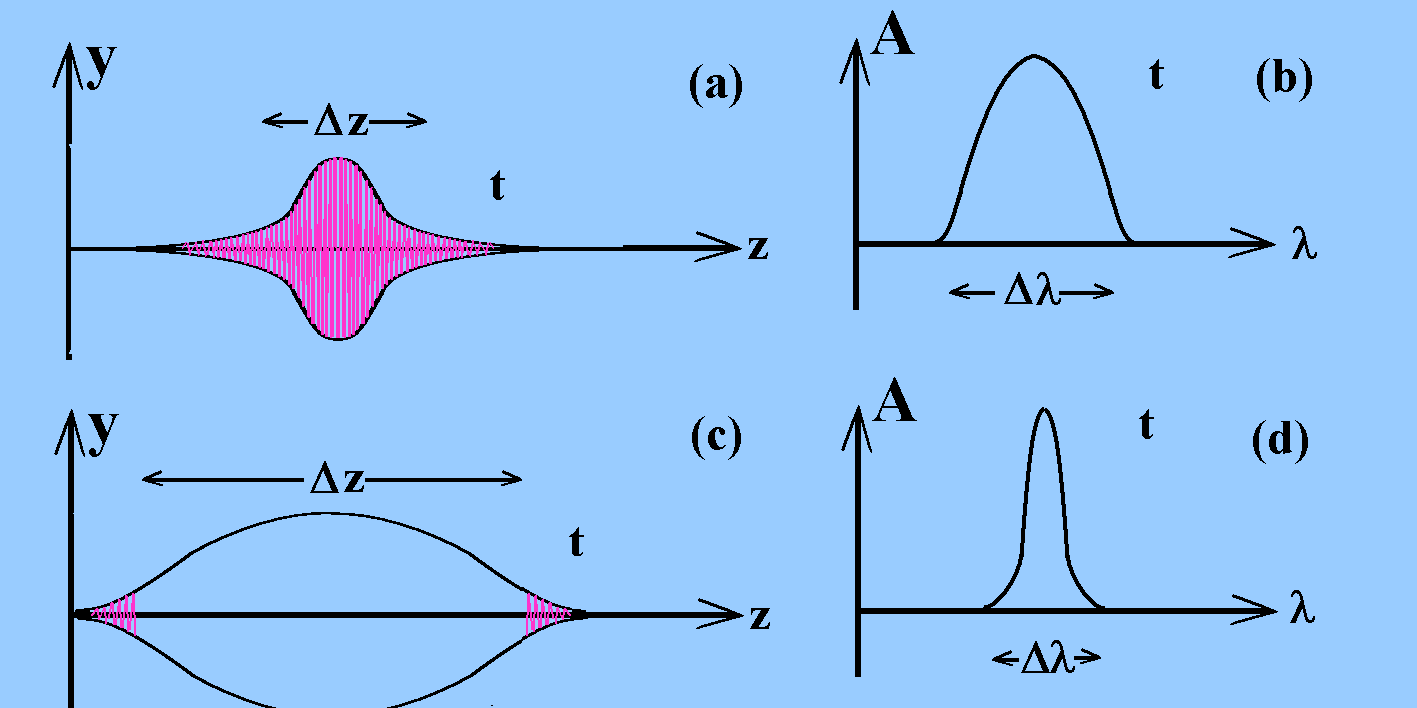
Auch in einem zweiten Beispiel kommen die angestrebten Un-be-stimmtheiten nicht vor. Ein klassisches ebenes Wellenpaket, z.B. von einer Schallwelle, soll betrachtet werden. In der schematischen Zeichnung sehen Sie zunächst bei einer Momentaufnahme zu irgendeiner Zeit t, wie die Auslenkung y vom Ort z längs der Ausbreitungsrichtung abhängt. Bei einer bestimmten Grundfrequenz ist die Amplitude für eine bestimmte Strecke Δz erhöht und dann wieder auf 0 abgesenkt (a), (c). Es kann sich offenbar nicht um eine monochromatische Welle mit einer festen Wellenlänge λ handeln, da diese ja unendlich ausgedehnt wäre. Ein solches Wellenpaket ist eine Überlagerung von beliebig vielen monochromatischen ebenen Wellen mit unterschiedlichen Wellenlängen λ. Ihre Wellenlängenverteilung (mit den jeweiligen Amplituden) ist in der jeweils zweiten Zeichnung (b), (d) schematisch dargestellt. So wie sich die örtliche Verteilung um einen mittleren Ort konzentriert, so konzentrieren sich die beteiligten Wellenlängen um eine mittlere Wellenlänge.
In der zweiten Zeile sehen Sie die entsprechenden Verhältnisse, wenn nur die Breite des Wellenpakets Δz vergrößert ist.
 |
|
| Versuch 3: Akustische
Analoga zur HUR_3
Auch hier bemerken Sie:
Genauso gilt das Umgekehrte. Wenn Sie hier schon quantenmechanisch denken würden, was hier sicher nicht zulässig ist, würden Sie sich daran erinnern, dass nach deBroglie mit der Wellenlänge λ ein Impuls p = h/λ verbunden ist. Der Wellenlängen"unschärfe" Δλ entspricht dann formal eine Impuls"unschärfe" Δp = h/λ2·Δλ, und Sie vermuten schon, dass gilt: |
Je größer die Orts"unschärfe" Δz, desto geringer ist die Impuls"unschärfe" Δp und umgekehrt.
In der klassischen Physik macht eine solche Aussage aber keinen Sinn.
I.9.1.3 Schwankungsbereiche beim Bohrschen Atommodell
Nach dem (mittlerweile überholten) Bohrschen Atommodell des Wasserstoff-Atoms umkreist ein Elektron den Atomkern auf einer Kreisbahn mit dem Radius r ähnlich wie ein Planet die Sonne umkreist. Dabei hat die Geschwindigkeit v einen bestimmten Betrag v und damit auch der Impuls p einen bestimmten Betrag p.
Die x-Koordinate des Elektrons schwankt zwischen -r und r mit dem Mittelwert 0. Es ergibt sich ein Schwankungsbereich Δx = r um den Mittelwert. Ganz entsprechend schwankt die x-Koordinate des Impulses zwischen px = -p und px = p, also innerhalb eines Bereichs der Breite Δpx = p (Abweichung vom Mittelwert). Es ergibt sich dann formal Δx·Δpx = r·p. Das gilt für einen Planeten wie für das Bohrsche Atommodell.
Wie Sie später kennen lernen werden, ist einer der Punkte, die den zeitweiligen Erfolg des Bohrschen Atommodells ausmachte, das Postulat Bohrs, dass der Drehimpuls gequantelt sein soll (was auch immer das hier heißen soll). In Formeln ausgedrückt: 2π·r·p = n·h (wobei n eine natürliche Zahl, h das Plancksche Wirkungsquant). Dann ergibt sich für den Grundzustand mit n = 1:
|
Δx·Δpx
= r·p = h/2π = |
Auch mit dieser halbklassischen "Herleitung" haben wir so etwas Ähnliches wie eine Unschärferelation erhalten. Sie besagt, dass die Schwankungsbereiche der Orts- und der zugehörigen Impulskoordinate gemeinsam eine bestimmte Größe nicht unterschreiten können.
Für die Schwankungsbereiche beim Bohrschen
Atommodell ergibt sich:
|
Je größer der Schwankungsbereich des Orts, desto kleiner ist der Schwankungsbereich des Impulses und umgekehrt. |
Beide gemeinsam können nicht beliebig klein gemacht werden.
Die Größe h = h/2π ist so klein,
dass sie in der klassischen Physik (wie etwa bei der
Planetenbewegung) durch 0 ersetzt werden kann. Deshalb spielt
die Relation dort keinerlei Rolle.
Die Gleichung ähnelt der HUR, hat aber mit ihr nichts zu tun, weil das Bohrsche Atommodell ein weitgehend klassisches Modell ist, bei dem Ort und Geschwindigkeit zu jedem Zeitpunkt einen bestimmten Wert haben, den man im Prinzip kennen könnte. Es entspricht bis auf das erwähnte Bohrsche Postulat einem Planetenmodell. Die HUR ist aber eine Folge der Tatsache, dass das Elektron Ort und Geschwindigkeit zugleich nicht besitzt.
Wenn an dem Bohrschen Modell überhaupt etwas Wahres ist, würde man nach dieser Regel vermuten, dass zu einer großen Ausdehnung des Atoms ein geringer Impuls(betrag) oder eine geringe Bahngeschwindigkeit v gehört und umgekehrt.
|
I.9.2.1 Eine halbklassische Betrachtung beim Doppelspalt . . . . . . . . . . . . . . . . .
|
|
I.9.2.1 Eine halbklassische Betrachtung beim Doppelspalt . . . . . . . . . . |
Beim Doppelspalt ist - ohne eine Messung - der Durchtrittsort in y-Richtung un-be-stimmt innerhalb eines Intervalls mit der Breite Δy = d/2 (Abweichung vom Mittelwert; das Teilchen könnte - klassisch gesprochen - durch die Öffnung A oder durch die Öffnung B gehen, und beide sind um den Spaltabstand d voneinander entfernt). Betrachten wir jetzt die Nachweisorte auf dem Schirm. Den vielen unterschiedlichen Nachweisorten in y-Richtung entsprechend muss man annehmen, dass auch die Impulskomponente in y-Richtung py un-be-stimmt ist.
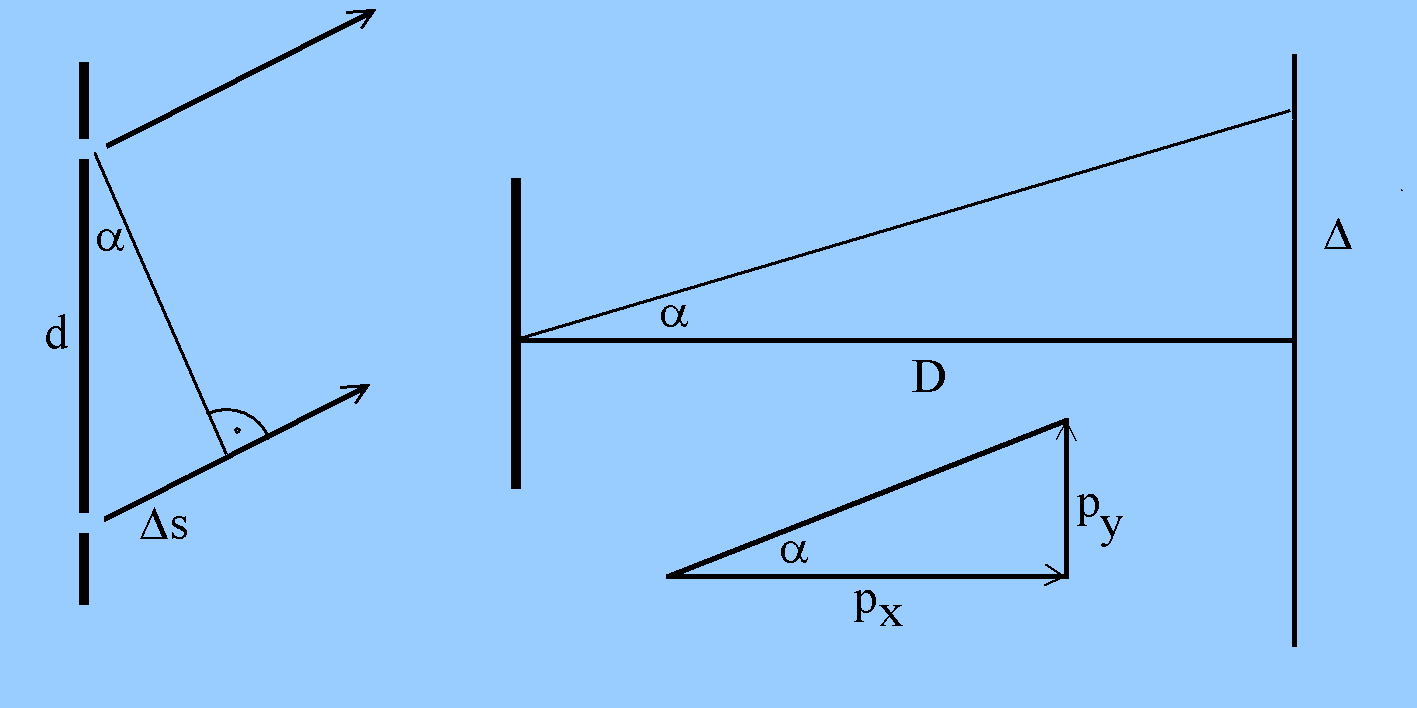 |
(Die Fragezeichen erinnern daran, dass es keine Bahnen
der Teilchen vom Doppelspalt zum Schirm gibt.)
Gemäß der Abbildung gilt - wieder klassisch argumentierend - Δ/D = py/px , wenn der Schirm um die Strecke D vom Doppelspalt entfernt ist, also py = Δ/D·px = Δ/D·h/λ . Es kommen offenbar auf dem Schirm weitgehend beliebige "Ablenkungen" Δ vor; was soll man dann als Maß fürdie Impulsunschärfe nehmen? |
| Das ist weitgehend Willkür. Ein großer Teil aller Teilchen wird im Hauptmaximum nachgewiesen. Entnehmen wir aus dessen Breite ein Maß für die Impulsunschärfe in y-Richtung, also aus dem Abstand der zwei dem Hauptmaximum links und rechts benachbarten Minima. | |
Dann gilt also für Δ = D λ/2d (Abstand der beiden symmetrisch gelegenen Minima von der Symmetrieachse): Δpy = py = Δ/D·h/λ = λ/2d · h/λ = h/2d . Damit erhalten Sie jetzt:
Δy · Δpy = d/2 · h/2d = h
Das Produkt der Unschärfen der Orts- und der Impuls-Koordinate jeweils in y-Richtung ist konstant und gleich dem Planckschen Wirkungsquant. Wir hätten auch den Abstand der symmetrisch gelegenen 5. Minima zur Berechnung von Δpy nehmen können; dann wäre noch ein Faktor 11/2 hinzugekommen. Wir machen sicher nichts falsch, wenn wir schreiben:
Δy · Δpy >= h
Klassisch wurde die Überlegung genannt, weil wir einen Zusammenhang zwischen Ablenkort Δund der Impulskoordinate in y-Richtung Δpy wie in der klassischen Physik ins Spiel gebracht haben, so als wären beide gleichzeitig be-stimmte Größen. Nur halbklassisch wurde sie genannt, weil aus der Interferenzfigur empirisch ein Maß für die quantenmechanische Impulsunschärfe gewählt wurde.
Für die Unschärfen ergibt sich wieder: Je größer die Orts-Unschärfe, desto kleiner ist die Impuls-Unschärfe und umgekehrt. Beide gemeinsam können nicht beliebig klein gemacht werden.
Bemerkenswert ist aber, dass diese Unschärfe jetzt nicht nur einen Bereich beteiligter Werte darstellen, sondern einen Bereich, in dem die zugehörige Messgröße un-be-stimmt ist. Würden wir also tatsächlich eine Messung für die Messgrößen durchführen, dann würden die Messwerte in den angegebenen Bereichen streuen, weil das Mikrosystem die betrachteten Eigenschaften vor der Messung nicht (exakt) besitzt. Deswegen sprechen wir statt von Unschärfe jetzt von der Maßgröße "Un-be-stimmtheit", und wir argumentieren mit einer Orts-un-be-stimmtheit Δy und einer Impuls-un-be-stimmtheit Δpy, jeweils für die gleiche Koordinatenrichtung.
|
Je größer die Orts-Un-be-stimmtheit, desto kleiner ist die Impuls-Un-be-stimmtheit für eine bestimmte Koordinatenrichtung und umgekehrt. |
Diese halbklassische Überlegung befriedigt nicht recht, da man doch zu sehr an Teilchen denkt, die gemäß der beteiligten Impulse scheinbar auf bestimmten Bahnen abgelenkt werden. Zudem müsste man in jeder neuen Situation und für jedes Paar komplementärer Messgrößen - Sie werden Beispiele noch erleben - jeweils mit neuen Tricks die Unschärfen abschätzen.
I.9.2.2 Die HUR als Folge von zwei komplementären Messgrößen, die ein Quantensystem nicht gleichzeitig als Eigenschaften hat
Deshalb wird die HUR in der gesicherten quantenmechanischen Theorie allein auf Grund der nicht gleichzeitigen Messbarkeit der zwei komplementären Messgrößen A und C ohne ein konkretes Modell und ohne Blick auf eine bestimmte Situation hergeleitet. Die Herleitung wird hier übersprungen, weil es doch mehr auf die Folgen der HUR ankommt. Das Ergebnis entspricht weitgehend dem eben hergeleiteten und kommt ohne die Willkür eines beteiligten Faktors k aus:
|
Wenn A eine Ortskoordinate und C die zugehörige Impulskoordinate ist, dann enthält k das Planck'sche Wirkungsquantum h und es gilt k = h/4·π. ΔA und ΔC sind dabei die mittleren quadratischen Abweichungen der zu erwartenden Messwerte vom Erwartungswert des Messwerts (in Formeln also ΔA = √ (<A>2 - <A2> ), ein etwas komplizierteres Maß für den "Schwankungsbereich" als bisher verwendet.
Jetzt endlich sind wir bei der Quantenphysik angekommen!
Für die Un-be-stimmtheiten von Orts- und Impulskoordinate, Δy und Δpy gilt danach tatsächlich die obige Beziehung, leicht modifiziert:
|
(Als Abkürzung wird hier h
(ausgesprochen: "h quer") verwendet, definiert durch h
= h/2π .)
I.9.2.3 Folgerungen und Deutung
(1) Die HUR in ihrer allgemeinen Form besagt: Ganz gleich in welchem Zustand sich ein Quantensystem befindet, die Un-be-stimmtheiten zweier komplementärer Messgrößen A und C können gemeinsam nicht beliebig klein gemacht werden.
(2) Zwei komplementäre Messgrößen können nicht gleichzeitig Eigenschaften des Systems sein. Dann müssten ja beide Un-be-stimmtheiten gleichzeitig 0 sein, was aber nach der HUR nicht möglich ist. Naja, das ist für uns nichts Neues. Nach Grundfaktum Ia wissen wir ja, dass ein Quantensystem nicht alle klassisch denkbaren Eigenschaften gleichzeitig hat, und wir wollten ja gerade zwei sich gegenseitig ausschließende, also komplementäre Messgrößen betrachten.
(3) Befindet sich das Quantensystem in einem Zustand, in dem die y-Koordinate des Orts Eigenschaft des Systems ist (im Beispiel des Doppelspalts also der Durchtrittsort - nach einer Messung), dann ist die Un-be-stimmtheit der Ortskoordinate gleich 0. Dann muss also die Un-be-stimmtheit der zugehörigen Impulskoordinate beliebig groß sein; die Impulskoordinate ist ja jetzt nicht Eigenschaft des Systems.
(4) Befindet sich das Quantensystem in einem Zustand, in dem die y-Koordinate des Impulses Eigenschaft des Systems ist (wieder nach einer Messung), dann ist die Un-be-stimmtheit von der Impulskoordinate gleich 0. Dann muss also die Un-be-stimmtheit der zugehörigen Ortskoordinate beliebig groß sein; die Ortskoordinate ist ja jetzt nicht Eigenschaft des Systems.
(5) Befindet sich das Quantensystem in einem Zustand, in dem die y-Koordinate des Impulses und des Orts beide nicht Eigenschaften des Systems sind, dann liefern Messungen für beide nur Messwerte innerhalb ihrer Un-be-stimmtheiten. Ihre Größe kann gemeinsame Grenzen nicht unterschreiten, die durch die HUR festgelegt sind.
(6) Wenn ein Teilchen nicht gleichzeitig Ort und Geschwindigkeit haben kann, dann kann es auch keine Bahn eines Teilchens geben. Von einem Ort r(t) würde sonst ja das Teilchen in der kurzen Zeit Δt mittels Δr = v·Δt zum Nachbarort r(t+Δt) der Bahn kommen.
(7) Die Un-be-stimmtheiten haben nichts mit einer technisch beschränkten Messungenauigkeit zu tun, sondern damit, dass die klassischen Größen Ort und Impuls (jeweils für eine bestimmte Koordinaten-Richtung), oder andere komplementäre Größen, nicht gleichzeitig beliebig genau existieren, bzw. einen Sinn haben.
(8) Das hat nichts damit zu tun, dass auch in der klassischen Physik Messwerte innerhalb gewisser Grenzen schwanken können, sei es, weil die Messgenauigkeit technisch nicht ausreicht, oder weil die Messgrößen selbst schwanken, wie das etwa bei einem um die Sonne laufenden Planeten der Fall ist, wenn wir eine Koordinatenrichtung allein betrachten, oder wenn wir Geschwindigkeiten von Atomen in einem Gas messen wollen, die thermischen Schwankungen unterliegen, die wir im Einzelnen nicht kennen. Durch die Heisenbergsche Un-be-stimmtheitsrelation werden Unschärfen oder Un-be-stimmtheiten beschrieben, die charakterisieren, wie weit Eigenschaften eines Quantensystems fehlen, und weniger, wieweit sie uns nur unbekannt sind (den Grad unserer Unkenntnis von ihnen).
(9) Die Gesamtheit aller möglichen Meßwerte und die Wahrscheinlichkeitsverteilung für ihr Eintreten spiegeln dennoch objektive, d.h. vom Beobachter unabhängige Eigenschaften des untersuchten Systems wieder.
(10) Was hat es zu bedeuten, dass die HUR ein Ungleichheitszeichen enthält? Packen wir das Problem umgekehrt an: Gibt es Situationen, wo das Gleichheitszeichen gilt?
|
Ja, z.B. für ein "Gaußförmiges"
Wellenpaket. Es besitzt eine Ortsabhängigkeit
entsprechend einer Gaußschen Glockenkurve und heißt auch
"Minimalpaket", weil eben das Produkt Δx ·Δp den
Minimalwert |
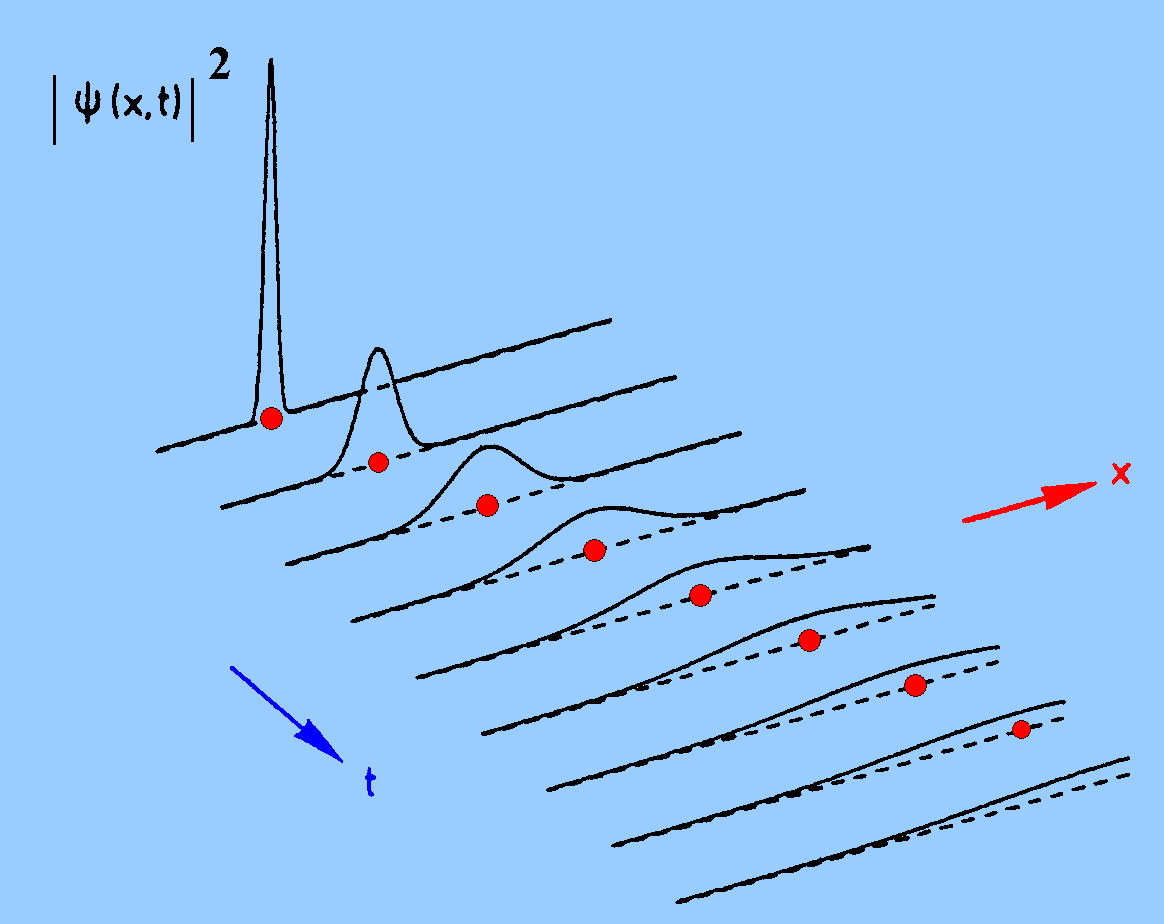
| In der Zeichnung nach Brandt u. Dahmen (The Picture book of quantum mechanics, Wiley 1985) ist ein nach rechts laufendes freies (kräftefreies) Wellenpaket dargestellt. Der rote Punkt stellt ein klassisches Teilchen dar, das sich mit gleicher mittlerer Geschwindigkeit nach rechts bewegt. |
Also: abhängig vom Zustand des Quantensystems treten die minimalen Unschärfen auf oder auch noch größere. Für viele Abschätzungen kann man so tun, als gelten die minimalen Unschärfen.
**) "Kohärente Zustände", z.B. für einen harmonischen Oszillator, oder eine Lichtwelle, laufen nicht auseinander. Ein Minimumpaket bleibt dort ein Minimumpaket.
.
(11) Wie könnte man die HUR in einem Zustand ψ überprüfen?
Es geht in der Quantenphysik immer um Voraussagen von Wahrscheinlichkeiten bei bestimmten Ensembles von gleichartigen Messungen.
Dabei ist es im Prinzip gleichgültig, ob das Ensemble dadurch entsteht, dass man ein und dasselbe Quantenobjekt immer wieder in den gleichen Zustand ψ präpariert, an dem dann die Messung unter gleichen Bedingungen vorgenommen wird, oder dass man nacheinander sehr viele identische, nicht unterscheidbare und nicht wechselwirkende Quantenobjekte nimmt, eines nach dem anderen in den gleichen Zustand präpariert und jeweils gleich Messungen unter gleichen Bedingungen vornimmt.
(Es ist auch denkbar, dass ein Vorrat identischer, nicht unterscheidbarer und nicht wechselwirkender Quantenobjekte in den betreffenden Zustand präpariert wird, an dem dann nach und nach die Messungen vorgenommen werden. Das ist aber bei Fermionen wegen des Pauli-Prinzips nicht möglich.)
Also:
(1) Das Teilchen wird in den Zustand ψ präpariert.
(2) Die Messgröße A wird durch eine Messung be-stimmt.
(3) Entweder wird jetzt das gleiche Teilchen wieder in den Zustand ψ präpariert oder es wird ein weiteres Teilchen des Ensembles verwendet.
(4) Daran wird jetzt die Messgröße B durch eine Messung be-stimmt.
Die Schritte (1) bis (4) werden sehr oft wiederholt. Aus den beiden Verteilungen für die erhaltenen Messwerte ergeben sich zwei Erwartungswerte <A> und <B>, aber auch die statistischen Streuungen ΔA und ΔB. Als Un-be-stimmtheiten ΔA und ΔB werden die Standard-Abweichungen von den jeweiligen Erwartungswerten (Mittelwerten) genommen. Für Abschätzungen wird oft die 2/3-Regel verwendet, die häufig, aber nicht immer, als Faustregel geeignet ist: "Ca. 2/3 aller Messwerte liegen in einer Standard-Abweichung symmetrisch um den Erwartungswert."
Eine Abschätzung für Ort x und Impuls p eines Teilchens im linearen Potenzialkasten finden Sie hier.
Die Messung zeigt für diesen Fall:
Δx · Δp >= h/4·π
I.9.2.4 Anwendung: Doppelspalt
Beim Doppelspalt heißt das: Macht man den Spaltabstand d immer kleiner, so geht man zu Zuständen über, in denen die y-Koordinate des Durchtritts-Orts immer genauer be-stimmt ist. Die Folge ist, dass die zugehörige Impulskoordinate immer weiter streuen muss: Das Hauptmaximum der Interferenzfigur wird immer breiter und damit auch alle Abstände innerhalb der Interferenzfigur.
I.9.2.5 Anwendung: Einfachspalt
Beim Einfachspalt: Macht man Δy immer kleiner (entsprechend der Spaltbreite b), weil man z.B. den Durchtrittsort innerhalb des Spalts durch Verringerung der Spaltbreite immer genauer bestimmt, dann wird Δpy immer größer: Es ergibt sich also die immer breiter werdende Interferenzfigur vom Einfachspalt.
I.9.2.6 Anwendung: Ein scheinbarer Widerspruch
Wie ist das aber: Betrachtet man einen bestimmten Punkt innerhalb der Interferenzfigur beim Doppelspalt, wo gerade ein Teilchen nachgewiesen wurde, dann ist für dieses Teilchen die y-Koordinate (auf dem Schirm) be-stimmt. Gleichzeitig sieht es so aus, als sei auch die entsprechende Koordinate des Impulses, py, jetzt be-stimmt - scheinbar im Widerspruch zur HUR.
Sie ahnen es schon: Hier muss man vorsichtiger sein und die Zeiten betrachten, zu denen der jeweilige Messwert gültig ist. Aus der Tatsache des Nachweises muss man auf die Ortskoordinate y unmittelbar nach dem Nachweis schließen; erst durch diese Messung "entsteht" ein Ort des Teilchens. Damit dies möglich wurde, war vor der Orts-Messung die y-Koordinate des Impulses einigermaßen genau be-stimmt***), so wie es sich aus der Rechnung von Abschnitt I.9.2.1 ergibt. Welchen Impuls py aber das Teilchen zu dem Zeitpunkt hat, zu dem die y-Koordinate be-stimmt ist, ist völlig un-be-stimmt. Das ist besonders drastisch einzusehen, wenn das Nachweisgerät das Teilchen absorbiert: dann ist mit dem Teilchen auch sein Impuls "verschwunden".
So gibt uns also dieses Beispiel keinen Anlass, an der Gültigkeit der HUR zu zweifeln.
***) Ganz genau ist py auch zu diesem Zeitpunkt nicht be-stimmt, da ja offen ist, durch welche Öffnung des Spalts das Teilchen hindurchgetreten ist.
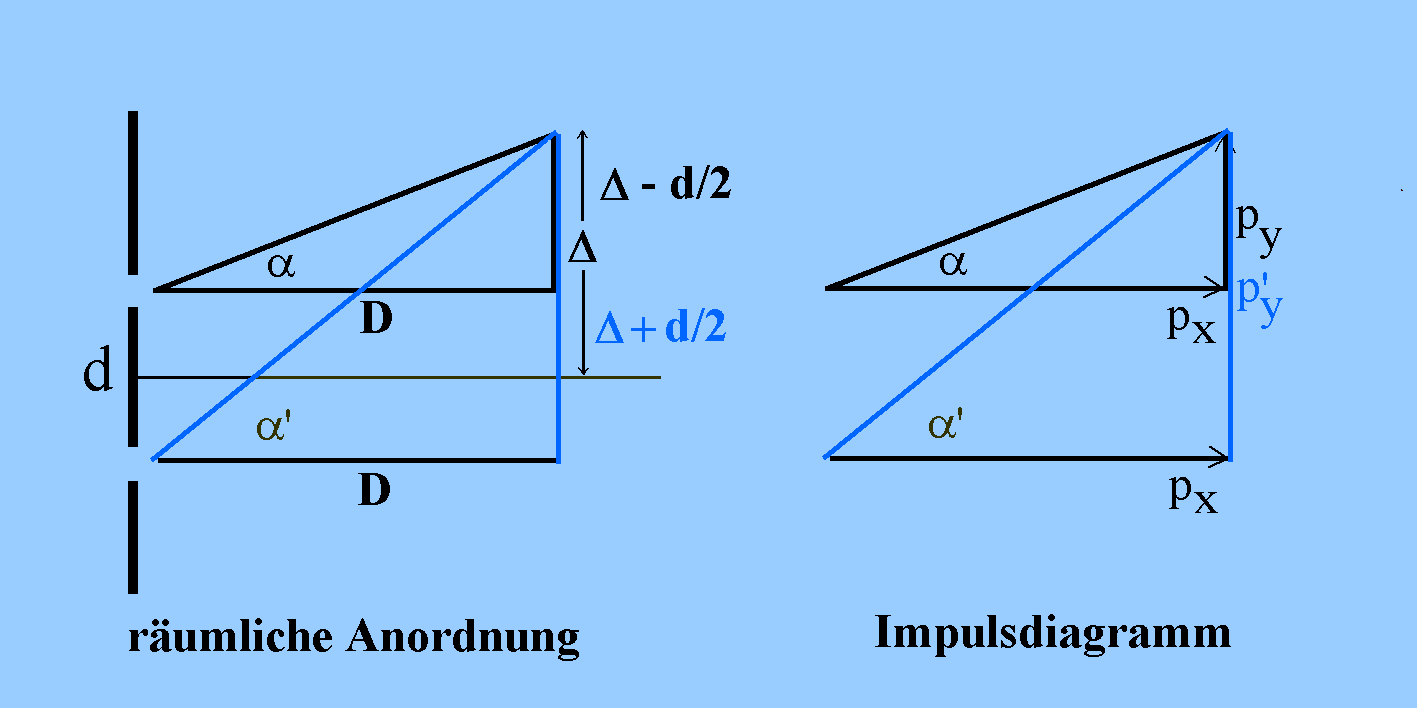
|
Nach der Abbildung (Siehe auch die Abb. von
I.9.2.1) gilt
py / px = (Δ-d/2)/D und py' / px= (Δ+d/2)/D , also Δpy = (py -py' )/2 = px.[(Δ+d/2) - (Δ-d/2 )] / 2D = px · d/2D = h/λ ·d/2D |
| Die sich daraus ergebende
Un-be-stimmtheit von py , Δpy ,
wächst mit dem Spaltabstand d.
Nachweis im 1. Maximum: Δ = λ· D/d, also mit Δy = Δ also Δpy · Δy = Δpy · Δ = h/2 |
|
Dies lässt sich wieder als HUR interpretieren (Ein Faktor bei h ist bei allen halbklassischen "Herleitungen" Willkür): Mit der Un-be-stimmtheit des Durchtrittsorts ist eine Un-be-stimmtheit des Impulses in y-Richtung verbunden. Diese hat nach der HUR wiederum zur Folge, dass der Nachweisort in y-Richtung eine Un-be-stimmtheit Δy = Δ hat, die mit zunehmendem Spaltabstand d kleiner wird. Das könnten Sie auch der Interferenzfigur ablesen!
Wenn Sie wollen, handelt es sich hier um eine weitere Variante einer halbklassischen Herleitung der HUR. Im Unterschied zu der von I.9.2.1 bringt man hier Unschärfen bzgl. Messungen am Schirm zusammen. Am Schirm wird die unmittelbar vor der Ortsmessung an einer bestimmten Stelle vorhandene Impulsunschärfe verglichen mit einem Maß der Ortsunschärfe solcher Ortsmessungen auf dem Schirm.
Bei I.9.2.1 wurde die Ortsunschärfe am Spalt verglichen mit einem Maß für die Impulsunschärfe, welches aus der Ablenkung bis zum Schirm hin gewonnen wurde.
I.9.2.7 Anwendung:
Elektronenbahn im Fadenstrahlrohr / Nebelkammer etc.
Wir wissen schon, dass es eine Bahn von Mikroteilchen nicht geben kann. Im Fadenstrahlrohr, im Fernseher oder Oszilloskop oder in der Nebelkammer sind wir aber - gemäß klassischer Betrachtung - bisher immer von Elektronenbahnen ausgegangen. Müssen wir unsere bisherigen Vorstellungen über den Haufen werfen? Eine Abschätzung mit Hilfe der HUR soll uns weiterhelfen.
Zum Nachweis eines Punktes der Bahn muss ein Atom oder Molekül
ionisiert werden. Die Ortsun-be-stimmtheit entspricht dem
atomaren Durchmesser von typisch Δx = 10 -10 m.
Daraus ergibt sich eine Impuls-un-be-stimmtheit Δp = h/Δx
» 10 -24 kgm/s durch die
Rückwirkung der Ortsmessung auf das Elektron im Strahl.
Andererseits besitzt ein Elektron im Fadenstrahlrohr bzw. in der
Fernsehbildröhre einen Impuls von typisch 10 -23
kgm/s bzw. 10 -22 kgm/s. Im Vergleich dazu ist die
Impuls-un-be-stimmtheit eine oder zwei Größenordnungen geringer.
Es hat also noch einen brauchbaren bzw. halbwegs guten Sinn, von
einer Bahn zu sprechen.
Die auf dem Bildschirm oder im Fadenstrahlrohr beobachtete Spur dürfen Sie nicht mit der Bahn eines Elektrons verwechseln. Durch vielfache Streuprozesse an Gasmolekülen oder Kristallkörnern im Bildschirm entsteht bereits klassisch eine Spur, die viel breiter ist als die Ortsun-be-stimmtheit.
I.9.2.8 Potentialtopf
Ein linearer Potentialtopf soll ein Bereich der Breite 2·a sein, in dem ein Teilchen ohne Energieverlust hin und her laufen kann, an dessen Wänden es verlustlos reflektiert wird. Klassisch gesprochen ist der Impuls des Teilchens dann +p oder -p mit dem Mittelwert 0. Also ist der Impuls un-be-stimmt innerhalb einer Un-be-stimmtheit Δp = p (Abweichung vom Mittelwert). Die Ortsunschärfe entspricht der halben Breite a des Potentialtopfs, also Δx = a. Damit erhalten wir:
| . | Δp · Δx = p · a >= h/4π. |
Es ergibt sich ein Mindestimpuls p = h/(4·π·a) und ein Mindestwert der kinetischen Energie p2/2m = h2/(32·m·π2·a2).
Andere Überlegungen zeigen, dass dies bis auf einen Faktor in der Größenordnung von 0,1 die Grundzustandsenergie E1 = h2/32ma2 ist. Das stärkt unser Vertrauen in solche Abschätzungen.
Klassisch gesprochen ist der Impuls des Teilchens +p oder -p. Aha, zwei klassisch denkbare Möglichkeiten; sollte dann nicht Interferenz die Folge sein? Natürlich, sie bewirkt zusammen mit den "Randbedingungen", speziell der Breite 2·a des Potentialtopfs, dass nur bestimmte Werte von p zu einem "Maximum" führen. Diese werden wir bei der ausführlicheren Behandlung des Potentialtopfes kennenlernen.
I.9.2.9 Abschätzung der Nukleonenenergie im Atomkern
Das Argument wird auch benutzt, um die Grundzustandsenergie eines Nukleons im Atomkern abzuschätzen. Das ist wichtig für die Frage, ob man die Nukleonen im Kern relativistisch behandeln muss oder auch nicht. Wie im letzten Beispiel wird der Minimalwert der Energie näherungsweise als Grundzustandsenergie genommen bzw. in der HUR das >=-Zeichen durch ein Gleichheitszeichen ersetzt.
Der Kernradius genügt der Regel r3= r03 · A mit der Massenzahl A, wobei r0 = 1,4·10-15 m. Nehmen wir für eine Abschätzung grob r = 10-14 m. Daraus folgt eine Ortsunschärfe Δx = r . Mit der Impulsunschärfe Δpx = p und der HUR ergibt sich p = h/4πr = 0,53·10-20 kgm/s und E = p2/2m = 0,8·10-14 J = 50 keV mit der Nukleonenmasse m = 1,67·10-27 kg. Also folgt eine Energie von 50 keV, die sehr viel kleiner ist als die Ruheenergie eines Nukleons von ca. 1 GeV. Sie ist also sicher nichtrelativistisch.
I.9.2.9 Abschätzung, dass sich im Atomkern keine Elektronen aufhalten können
Beim ß-Zerfall sendet ein Atomkern ein Elektron mit einer typischen Energie von 3 MeV aus. Die zunächst scheinbar widersinnige Frage ist also, ob dieses negative Elektron sich vorher im positiven Atomkern aufhielt. Wir nehmen versuchsweise an, dass sich ein Elektron im Atomkern hin und her bewegt. In der vorigen Rechnung ist m durch die Elektronenmasse zu ersetzen. Es ergibt sich dann ein ca. 2000 mal größerer Wert E = 100 MeV = 0,1 GeV, was weit über der Energie von 3 MeV liegt. Die Abweichung ist zu groß, als dass man annehmen könnte, dass sich im Atomkern Elektronen bewegen. Erst beim Zerfall also können Elektronen mit dieser hohen Energie entstehen. Sie müssen sofort den Kern verlassen.
I.9.2.10 Zeit-Energie-Unschärfe
Die Zeit-Energie-Unschärfe spielt eine Sonderrolle in ihrer Herleitung; ihre physikalischen Folgen sind mindestens genauso wichtig wie die Orts-Impuls-Un-be-stimmtheit. Ihre Sonderrolle ergibt sich daraus, dass die Zeit t keine Messgröße im Sinne der gegenwärtigen Quantentheorie ist. Deshalb gibt es nach der Quantentheorie auch nicht den Begriff der Un-be-stimmtheit für die Zeit. Diese ist ein im Prinzip immer messbarer Parameter. Wir wollen uns nicht weiter darum kümmern, wie die Zeit-Energie-Unschärfe-Relation hergeleitet wird. Im Zusammenhang mit der Zeit-Frequenz-Unschärfe-Relation haben wir sie hinreichend plausibel gemacht. Viel interessanter sind ihre Folgen. Betrachten Sie ein Wellenpaket, das manchmal auch Wellenzug genannt wird:
(a) Zeit-Frequenz-Unschärfe:
|
|
1. Je kurzzeitiger der Wellenzug, (Δt klein) desto größer ist der Bereich der beteiligten Frequenzen (Δf groß), für Licht übersetzt ins Quantenbild: desto größer ist der Bereich der beteiligten Photonenenergien. Das ist z.B. der Fall beim Licht glühender Metalle oder dichter Gase.
2. Je "monochromatischer" der Wellenzug (Δf klein), desto langzeitiger ist der Vorgang (Δt groß), z.B. die Dauer der Lichtemission eines Atoms beim Laser (Kohärenzlänge)
3. Beim Emissionsvorgang eines Photons durch ein Atom: je schmaler die Spektral-Linie (Δf oder Δλ klein), desto länger die Zeitdauer des Emissionsvorgangs (Δt groß) (Vgl. Lebensdauer und Linienbreite).
4. Möchte man ein sehr präzises Licht-Signal einer ganz bestimmten Frequenz f erhalten, also Photonen mit einer ganz bestimmten Energie und extrem geringen Energie-un-be-stimmtheit, dann muss man einen sehr langlebigen atomaren Zustand verwenden. Das ist z.B. wichtig, wenn man extrem genaue Atomuhren bauen möchte (u.a. Nobelpreis 2005 an John L. Hall und Theodor W. Hänsch)
b) Zeit-Energie-Unschärferelation
| ΔE · Δt >= h/2·π |
I.9.2.11 Amplituden-Phasen-Unschärfe bei Licht
Laserlicht lässt sich durch so genannte kohärente Zustände beschreiben, die die größte Annäherung der Quantenphysik an klassische elektromagnetische Welle darstellen.Wie einer der Nobelpreisträger von 2005, Roy J. Glauber, schon 1963 gezeigt hat, sind das Zustände mit un-be-stimmter Photonenzahl. Dabei entspricht das Betragsquadrat der Amplitude von der elektrischen Feldstärke der Teilchenzahl N. Amplitude, Teilchenzahl und Phase sind damit Messgrößen, die nicht alle gleichzeitig Eigenschaften des Lichts sind, d.h. nicht gleichzeitig messbar sind. Wie in I.9.2.2 bereits erwähnt wurde, folgt daraus eine Unschärferelation. Sie besagt:
|
Amplitude bzw. Teilchenzahl N und Phase sind bei Licht nicht gleichzeitig be-stimmt. |
- Es sind Zustände mit scharfer Amplitude bzw. scharfer Teilchenzahl N denkbar. Dabei ist die Phase völlig un-be-stimmt. Licht in solchen Zuständen ist deshalb nicht interferenzfähig im klassischen Sinn, jedoch im Sinn der Einteilchen-Interferenz.
- Es sind auch Zustände mit scharfer Phase denkbar. Dabei ist die Amplitude bzw. Teilchenzahl völlig un-be-stimmt. Licht in solchen Zuständen ist deshalb nicht interferenzfähig im klassischen Sinn.
- Es gibt ferner Zustände mit un-be-stimmter Teilchenzahl ( kohärente Zustände ). Weil für die Un-be-stimmtheit der Teilchenzahl bei der vorliegenden Poisson-Verteilung gilt: ΔN = √N, wächst die Unschärfe ΔN der Teilchenzahl N mit zunehmender Teilchenzahl. Aber die relative Teilchenzahl-Un-be-stimmtheit ΔN/N = 1/√N strebt für N -> unendlich gegen 0. Das heißt, die Teilchenzahl ist zwar nur sehr unscharf messbar, aber im Vergleich zur sehr großen mittleren Teilchenzahl ist die Unschärfe kaum zu bemerken. Ähnlich ist die Phasenunschärfe beschränkt. D.h. bei solchen kohärenten Zuständen mit großer mittlerer Teilchenzahl lässt die HUR quasi scharfe Amplitude und quasi scharfe Phase zu: in solchen Zuständen ist die elektromagnetische Welle interferenzfähig im Sinne einer klassischen Welle. Das kennen wir von der Laser-Strahlung!
I.9.2.12 E-B-Unbe-stimmtheit bei Licht
|
|
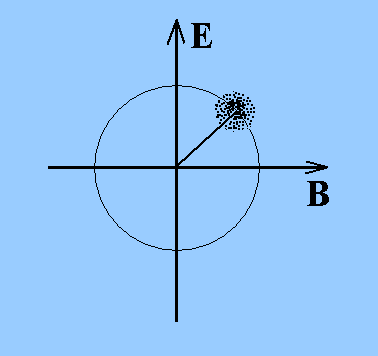
Eine andere Darstellungsweise der
verschiedenen Sorten von Licht besteht darin, dass man
eine Komponente der elektrischen Feldstärke E aufträgt
gegenüber einer Komponente der magnetischen Flussdichte B.
Bei einer ebenen Welle mit linearer Polarisation nimmt man
dann senkrechte Komponenten, z.B. Ex und By,
bei einer mit zirkularer Polarisation auch
gleichgerichtete.
Es stellt sich heraus, dass bei einer quantenphysikalischen Beschreibung von Laserzuständen beide Messgrößen un-be-stimmt und auch nicht gleichzeitig messbar sind. In der Abbildung wird deshalb symbolisch eine Punktwolke gezeichnet. Für beide Messgrößen gibt es also eine HUR, die hier (bei kohärenten Zuständen und bei einem geeigneten Maßsystem für E und B) die Form hat: |
|
| Elektrische und magnetische Feldstärke in einer bestimmten Koordinatenrichtung, z.B. der y-Richtung, bei einem quantenphysikalischen Laserzustand mit zirkularer Polarisation. Im Laufe der Zeit wandert die Punktewolke auf dem Kreis. (Bei einer linearpolarisierten Welle würde man statt E und B die so genannten „Quadraturkoeffizienten“ X und Y auftragen.) |
| ΔE · ΔB = 1/2 · Eph
· k
mit einer vom Maßsystem abhängigen Konstanten k und der Photonenenergie Eph |
(Weil hier das >=-Zeichen durch ein Gleichheitszeichen ersetzt ist, spricht man von "minimalen" Unschärfen in kohärenten Zuständen.)
Bei klassischem Licht in kohärenten Zuständen sind in diesem Fall beide Un-be-stimmtheiten unabhängig von den Messwerten selbst. Bei sehr großer Photonenzahl ergeben sich sehr große Amplituden für E und B, und die relativen Un-be-stimmtheiten ΔE/E und ΔB/B werden sehr klein. Die konstanten Un-be-stimmtheiten wirken sich dann kaum mehr aus:
|
Bei sehr großer Photonenzahl verhält sich Laserstrahlung wie eine klassische elektromagnetische Welle. |
Sie verstehen jetzt, weshalb trotz Gültigkeit der Quantentheorie Experimente zuerst zu klassischen elektromagnetischen Wellen führten.
( Bei einer zirkularpolarisierten Welle sind jeweils gleichgerichtete Komponenten von E und B un-be-stimmt. Trägt man hier eine Komponente der elektrischen Feldstärke E auf gegenüber einer gleichgerichteten Komponente der magnetischen Flussdichte B, z.B. die gleichgerichteten Komponenten Ey und By, dann erhält man eine ausgedehnte Punktwolke, die im Laufe der Zeit auf einem Kreis um den Ursprung wandert (vgl. Abb.).
Man kann Zustände herstellen mit sehr kleiner Un-be-stimmtheit von Ey. Dann ist By sehr un-be-stimmt (und umgekehrt). Die Punktewolke wird dann in eine Koordinatenrichtung „gequetscht“. Solche Zustände beschreiben „gequetschtes Licht“ bzw. "nicht-klassisches Licht", von dem man sich in Zukunft wichtige Anwendungen verspricht.)
|
I.9.3 Komplementarität und HUR
. . . . . . . . . . . . . . . . .
|
|
I.9.3 Komplementarität und HUR . . . . . . . . . . . |
Zwei komplementäre (genauer: nicht gleichzeitig messbare) Messgrößen können nicht gleichzeitig Eigenschaften eines Quantensystems sein. Das spiegelte sich auch in der HUR wider. Es ergeben sich jedoch weitere Folgerungen aus der Komplementarität.
(a) Mit den Methoden der Quantentheorie wird eindeutig nachgewiesen: Wenn zwei Messgrößen nicht gleichzeitig messbar (nicht gleichzeitig Eigenschaften eines Systems sind), dann gilt für sie zwangsläufig eine HUR. Der Nachweis soll auch hier übergangen werden.
(b) Auf der anderen Seite hat sich bei vielen Experimenten herausgestellt, dass sich Welcher-Weg-Information und Interferenz gegenseitig ausschließen. Die beiden Aspekte, Welcher-Weg-Information und Interferenz, sind also auch in gewisser Weise komplementär zueinander. Man kann diese Aussage auch aus einem Zusammenhang mit einer HUR herleiten. (Vgl. Darstellung nach Zeilinger).
Zu (a): Manchmal versucht man auch klassisch zu begründen, weshalb zwei Größen nicht gleichzeitig messbar sind. Danach werde das System durch die erste Messung so "gestört" (vielleicht in Form eines Stoßes von energiereichen Photonen bei der Beleuchtung eines Teilchens), dass die zweite Messung nicht mehr den Ausgangszustand antrifft. Durch eine solche klassisch vorgestellte Störung wird dann manchmal auch die HUR erklärt. Tatsächlich soll "Störung" aber nach heutiger Auffassung nicht heißen, dass durch den Messvorgang ein Teilchen im klassischen Sinn z.B. einen Stoß bekommt, sondern, dass durch die erste Messung eine Eigenschaft be-stimmt wurde, die vorher i.A. nicht be-stimmt war. Das ist ein Vorgang, der auch durch noch so raffinierte Tricks nicht vermieden werden kann, dessen Auswirkung auch nicht beliebig klein gemacht werden kann.
Es gibt klassische Modelle, die mit Methoden der klassischen Physik zeigen, dass eine Messung vorherige Messergebnisse ungültig macht, bzw. halbklassische Modelle, die zu Beziehungen führen, die der HUR sehr ähnlich sehen (S. I.9.2.1 ). Dazu gehört auch das fiktive "Heisenbergsche Elektronenmikroskop" oder Beugung und Interferenz an Einfach- oder Doppelspalt. Bei ihnen stellt man sich in der Regel vor, dass das Messobjekt durch den "Photonenbeschuss" bei der Orts-Messung im Sinne eines mechanischen Stoßes Zusatz-Impuls bekommt, der für spätere Impuls-Messungen eine andere Situation herstellt. Möglicherweise wurde die HUR historisch auch so "hergeleitet". In Wirklichkeit haben solche mehr oder weniger klassischen Modelle wenig Erklärungswert; die HUR wird seit Etablierung der QM in den dreißiger Jahren direkt aus der nicht gleichzeitigen Messbarkeit zweier Messgrößen hergeleitet. Bei dem folgenden Experiment wird zudem dafür gesorgt, dass die mechanische "Störung" bei der Ortsmessung vernachlässigbar klein ist. Und (zurück) wie das ohnehin in der Physik so üblich ist, ergibt sich der Wahrheitswert einer physikalischen Aussage nicht so sehr aus der Qualität der Herleitung, als vielmehr aus der Tatsache, dass nie ein Widerspruch zu Experimenten beobachtet wurde.
Wichtiger als eine Herleitung der HUR ist es für uns ohnehin, mit ihrer Hilfe quantenphysikalische Beobachtungen und Anwendungen zu erklären oder plausibel zu machen.
Zu (b): Scully, Englert und Walther dachten sich einen Mechanismus für eine "störungs"freie Welcher-Weg-Messung von Atomen aus, bei dem die HUR keine offensichtliche Rolle spielt. Man kann also in solchen Systemen nicht mehr argumentieren (wie das früher manchmal geschah), dass die Welcher-Weg-Messung die durch den Doppelspalt tretenden Teilchen so beeinflusst (im Sinne z.B. von mechanischen Stößen), dass sie nicht mehr interferenzfähig sind. Dennoch verschwindet auch beim Mechanismus dieser Autoren die Interferenz, sobald WWI gewonnen wird.
Beim Mechanismus dieser Autoren markieren Photonen den Weg der Atome, Photonen, die in Hohlraumresonatoren vor den Spaltöffnungen zurückbleiben, je nach der Spaltöffnung, die die Atome passierten, während die Atome am Schirm nachgewiesen werden. Die mechanische "Störung" bei der Ortsmessung ist ja eben vernachlässigbar klein, weil nur sehr niederenergetische Photonen in den Hohlraumresonatoren beteiligt sind. In dieser Situation entstehen verschränkte Zustände zwischen den beobachteten Atomen und den Photonen. Solche verschränkte Zustände lassen Interferenz nicht zu, da sie sich ihre zwei Anteile gemäß der zwei klassisch denkbaren Weg-Möglichkeiten nicht ganz am gleichen Ort überlagern. Z.B. überlagern sich zwar die atomaren Anteile auf dem Schirm, aber die Photonen-Anteile sind in einem von zwei Resonatoren vor den Spaltöffnungen "zurückgelassen" worden und können sich nicht überlagern, damit auch nicht die zugehörigen verschränkten Zustände als Ganze.
Wichtig ist das allgemeinere Ergebnis: Auch in dieser Situation schließen sich WWI und Interferenz gegenseitig aus. Man könnte auch dies eine Folge der Komplementarität nennen.
Zu (a) Auf Listen solcher komplementärer Messgrößen wurde bereits hingewiesen. Dabei sind Paare aus reinen Teilchengrößen, andere, bei denen Teilchen- und Wellengrößen gemischt vorkommen (wie etwa bei einer elektromagnetischen Welle ihre Phase und Teilchenzahl), und wieder andere, die sich ganz auf Wellengrößen beziehen, wie etwa Amplitude und Phase bei einer elektromagnetischen Welle. Für alle diese Paare komplementärer Messgrößen gibt es dann jeweils eine Un-be-stimmtheits-Relation.
I.9.4 Unterschied Un-be-stimmtheit und Ungewissheit - Schrödingers Katze
Es handelt sich um ein von Schrödinger erfundenes Paradoxon, das seit seiner Erfindung 1935 immer wieder zu Diskussionen herausforderte und so ein tieferes Verständnis der Quantentheorie auslöste. Es wird auch heute noch kontrovers diskutiert. Hier wird eine Variante von Green wiedergegeben, die mir schon während des Studiums als besonders einsichtig vorgestellt wurde.
In einem lichtdichten Kasten ist eine Katze eingesperrt. Ferner befindet sich in dem Kasten ein Strahlteiler, ein Photonenzähler und ein Mechanismus, der die Katze auf eine schnelle und schmerzlose Weise umbringen kann. Wird ein einfallendes Photon am Strahlteiler reflektiert, passiert gar nichts. Wird es aber durchgelassen, so wird es vom Zähler registriert. Dieser löst dann den Mechanismus aus, der die Katze umbringt. Wenn man ein Photon in den Kasten geschickt hat, ohne ihn zu öffnen, weiß man also nicht, ob die Katze tot oder lebendig ist. Schrödinger behauptete, dass sich die Katze in einem Überlagerungszustand von tot und lebendig befinde, für eine makroskopische Katze eine sehr ungewohnte Situation, die man sonst in der makroskopischen Welt nicht kennt. Man sprach davon, dass es un-be-stimmt sei, ob die Katze tot oder lebendig ist, während der gesunde Menschenverstand einen eindeutigen Zustand für die Katze erwartet. Das sah Schrödinger als einen Mangel der Quantenphysik an. Andere Physiker (wie H.S. Green) fanden gar nichts Ungewöhnliches an der Situation. Sie gingen davon aus, dass die Un-be-stimmtheit nur andauere bis zum Ansprechen des Zählers bzw. zur Auslösung des Tötungsmechanismus. Von da ab sei das Schicksal der Katze nicht mehr un-be-stimmt, sondern nur mehr ungewiss bis zur Öffnung des Kastens.
Moderne "Dekohärenzexperimente" bestätigen diese Sicht. Danach machen sich bei einem großen System (wie schon ein großes Molekül, erst recht wie der Zähler oder wie eine Katze) Ankopplungen an die Umgebung , z.B. mit Hilfe von energiearmen Photonen so stark bemerkbar, dass nach kürzester Zeit jeder un-be-stimmte Zustand (hier: Überlagerungszustand von tot und lebendig) in einen be-stimmten (hier: tot oder aber lebendig) übergeführt ist, um so schneller, je größer das System ist. Bei Rubidium-Molekülen fand man bereits die unvorstellbar kleine Dekohärenz-Zeit von 10-23 s, nach der also ein un-be-stimmter Molekülzustand durch Wechselwirkung mit der Umgebung in einen be-stimmten übergegangen ist.
I.9.5 Deutung der HUR mit "Grundfakten"
- Nichtexistenz aller Eigenschaften gleichzeitig: Es
gibt Paare von Messgrößen, die nicht beide gleichzeitig
messbar sind, die nicht gleichzeitig Eigenschaften des
Quantensystems sind. Vielleicht sind sie sogar beide nicht
Eigenschaften im vorliegenden Zustand; dennoch hängen sie
gesetzmäßig zusammen, könnte jede für sich Eigenschaft sein.
Wenn sie beide nicht Eigenschaft sind, streuen deshalb
beide Messwerte bei wiederholten Messungen.
- Das wird genauer beschrieben durch den Begriff der Maßgröße
"Un-be-stimmtheit": In diesem Fall sind beide
Messgrößen un-be-stimmt. Die HUR macht gesetzmäßige Aussagen
über die Mindestgröße der gemeinsamen Un-be-stimmtheit. Wenn
der Zustand so ist, dass die eine Messgröße, A, in dem
Zustand ungefähr be-stimmt ist, muss der Zustand Anteile von
sehr vielen möglichen Beiträgen der komplementären Größe, C,
enthalten. Diese ist dann gleichzeitig sehr un-be-stimmt.
Entsprechendes gilt umgekehrt.
- Die HUR sagt damit, dass der Eingriff des Messvorgangs
bei einer der beiden Größen mit seiner Auswirkung auf eine
Messung der zweiten Größe nicht beliebig klein gemacht werden
kann (aber nicht im Sinne einer mechanischen "Störung").
- Das ist möglich, weil ja auch die objektive Wahrscheinlichkeit für das Eintreten von Messwerten gesetzmäßig durch die Quantentheorie beschrieben wird. Es wird gesetzmäßig gesagt, wie groß die (Streu-)Bereiche gemeinsam mindestens sein werden, in denen Messwerte eintreten werden, wenn reale Messungen durchgeführt werden.
Zusammenfassend und um das Verständnis zu verfestigen, können Sie einen Fragebogen zur HUR bearbeiten.
|
I.9.6 Die Kopenhagener Deutung der Quantentheorie . . . . . . . . . . . . . . . . .
|
|
I.9.6 Die Kopenhagener Deutung der Quantentheorie . . . . . . . . . . . . . . |
|
I.9.6 Die Kopenhagener Deutung der Quantentheorie . . . . . .. . .
. . . . |
Unter "Kopenhagener Deutung" werden üblicherweise leicht verschiedene Konzepte dargestellt. Sie ist so benannt, weil sie durch Niels Bohr und dem Kreis um ihn, dem auch Werner Heisenberg und Max Born angehörten, ursprünglich in den zwanziger und dreißiger Jahren des letzten Jahrhunderts in Kopenhagen erarbeitet worden ist. Der heutigen - in den meisten Quantenphysik-Büchern dargestellten Form - entspricht im Kern etwa folgende Auffassung:
(1) Die Physik darf nur Aussagen machen über Dinge, die durch reale Messungen überprüfbar sind. Dazu braucht man reale Messgeräte, also makroskopische Geräte. Diese Forderung liegt ebenso wie der Relativitätstheorie auch der Quantentheorie zugrunde. Mit Messgeräten kann aber prinzipiell nur nach Messgrößen bzw. Begriffen gefragt werden, die außerhalb der atomaren Größenordnungen bewährt sind, also z.B. nach Ort und Geschwindigkeit eines Teilchens, so als ob es ein makroskopisches Teilchen wäre. (Präambel )
Für den atomaren Bereich haben diese Begriffe nur mehr einen beschränkten Sinn. Sie erhalten erst einen Sinn durch eine Messung. So gibt es zum Beispiel im atomaren Bereich keine Bahn eines Photons von der Lichtquelle zum Nachweisort als Aufeinanderfolge von Orts-Geschwindigkeits-Situationen. (Grundfaktum Id)
(2) Die Durchführung einer Messung bedeutet damit eine Frage an die Natur im Sinne der makroskopisch definierten Begriffe, etwa in dem Sinn „Elektron, angenommen du hast einen Ort, wo bist du dann?“ (Grundfaktum IVa bzw. Ib)
Die Natur reagiert darauf unterschiedlich:
a) Wenn das Elektron in einem Zustand ist, in dem es die Eigenschaft "be-stimmter Ort" hat, dann gibt sie auch immer die gleiche richtige Antwort. (Grundfaktum IVb und IVc)
b) Ist das Quantensystem aber in einem Zustand, in dem es diese Eigenschaft nicht hat, dann reagiert die Natur auf die nicht ganz passend gestellte Frage mit streuenden Antworten, einmal mit diesem Ergebnis, einmal mit jenem: Zwangsläufig streuen in diesem Fall die Messwerte selbst bei größter Meßgenauigkeit statistisch um einen Mittelwert. (Grundfaktum IVd und IIb)
(3) Größen, die nicht gleichzeitig einen Sinn haben, nicht gleichzeitig be-stimmt sind, heißen komplementär. Komplementäre Größen (wie z.B. Ort und Geschwindigkeit eines Teilchens oder die Komponenten der Feldstärke Ex und Ey oder Ex und Bx ) sind nicht gleichzeitig messbar, d.h. sie sind nicht gleichzeitig Eigenschaften eines Systems. (Grundfaktum IVd und IIb und Ia)
Für sie kann eine Heisenbergsche Un-be-stimmtheitsrelation formuliert werden. Die Unschärfen der Heisenbergschen Un-be-stimmtheitsrelation kennzeichnen dabei das Fehlen von Eigenschaften des physikalischen Systems und nicht nur das Fehlen von Kenntnis. Sie werden deshalb Un-be-stimmtheiten genannt, weniger genau eben als Unschärfen.
Die Quantentheorie zeigt, wie man ausgehend von der nicht gleichzeitigen Messbarkeit von zwei Größen, also der Tatsache, dass sie nicht gleichzeitig Eigenschaften des Systems sind, zwangsläufig auf eine Un-be-stimmtheitsrelation für die beiden Größen schließen muss.
(4) Die Gesamtheit aller möglichen - also auch der streuenden - Messwerte spiegelt dennoch objektive, d.h. vom Beobachter unabhängige, Eigenschaften des untersuchten Systems wieder, für die aber keines der Modelle 'Welle' oder 'Teilchen' voll angemessen ist. Ebenso werden objektive Wahrscheinlichkeiten für das Eintreten von Messwerten gesetzmäßig beschrieben. (Grundfaktum IIa und IIc)
(5) Damit man dennoch über die Natur reden kann, ist es manchmal zweckmäßig, von Wellen oder Teilchen zu reden. Damit ist gemeint, dass man beide Begriffe als Modelle der Wirklichkeit auffasst, nicht als Begriffe, die der Wirklichkeit selbst zukämen. Es ist manchmal also zweckmäßig, das eine oder aber das andere der beiden Modelle zu verwenden, oder aber ein ganz anderes ("Modellphilosophie"). Für eine bestimmte Versuchsanordnung ist ein bestimmtes Modell eventuell zweckmäßiger als ein anderes, um das Verhalten anschaulich zu beschreiben. Die Fragen an die Natur entsprechen Fragen im Sinne eines dieser Modelle. Doch weiß jeder Physiker, dass er damit nicht die Natur 'an sich' beschreibt, sondern nur beschränkt zutreffende Bilder von ihr. Mit der abstrakteren Quantentheorie beschreibt er dennoch das atomare Geschehen vollständig, aber in mathematischer Sprache, nicht mehr anschaulich. Für verschränkte Zustände passt keines der Modelle 'Welle' oder 'Teilchen' in ihrer naiven Form wegen der "Nichtlokalität" ("Fernwirkungslosigkeit") (Grundfaktum V)
(6) Mit der Wellenfunktion ψ wird in der Schrödingerschen Formulierung der Quantentheorie dann weniger die Ausbreitung und Überlagerung von irgendetwas Materiellem (also nicht von realistischen Wellen) erfasst, sondern ein Verfahren zur Berechnung von Wahrscheinlichkeiten für das Eintreten von Messwerten bei Berücksichtigung verschiedener ununterschiedener Möglichkeiten, die bei einem Versuch nach klassischer Vorstellung eintreten können.
Aufgabe:
Richard Feynman (1918 - 1988, Nobelpreis 1965) schreibt in seinen „Lectures on Physics“ zur Quantentheorie:
„Even the experts do no understand it the way they would like to, and it is perfectly reasonable that they should not, because all of direct, human experience and of human intuition applies to large objects.“
oder auch:
"Ich glaube, mit Sicherheit behaupten zu können, dass heutzutage niemand die Quantenmechanik versteht."
Demgegenüber schreibt Anton Zeilinger, einer der wichtigsten derzeit forschenden Quantenphysiker (Einsteins Schleier, 2003):
"Die Annahme, dass sich diese Wahrscheinlichkeitswellen tatsächlich im Raum ausbreiten, ist also nicht notwendig - denn alles, wozu sie dienen, ist das Berechnen von Wahrscheinlichkeiten. Es ist daher viel einfacher und klarer, die Wellenfunktion ψ nicht als etwas Realistisches zu betrachten, das in Raum und Zeit existiert, sondern lediglich als mathematisches Hilfsmittel, mit dessen Hilfe man Wahrscheinlichkeiten berechnen kann."
und auch in "Quantum Teleportation", Scientific American, April 2000, S. 32 - 41:
"Indeed, following Bohr, I would argue that we can understand quantum mechanics, if we realize that science is not describing how nature is, but rather expresses what we can say about nature. This is where the current value of fundamental experiments such as teleportation lies: in helping us to reach a deeper understanding of our mysterious quantum world."
Vergleichen Sie die beiden Ansichten! Was bedeutet "Verstehen" für die beiden Autoren?