Versuch 1: Untersuchungen an einem Knall - Frequenz-Zeit-Unschärfe

a) Vorbereitung:

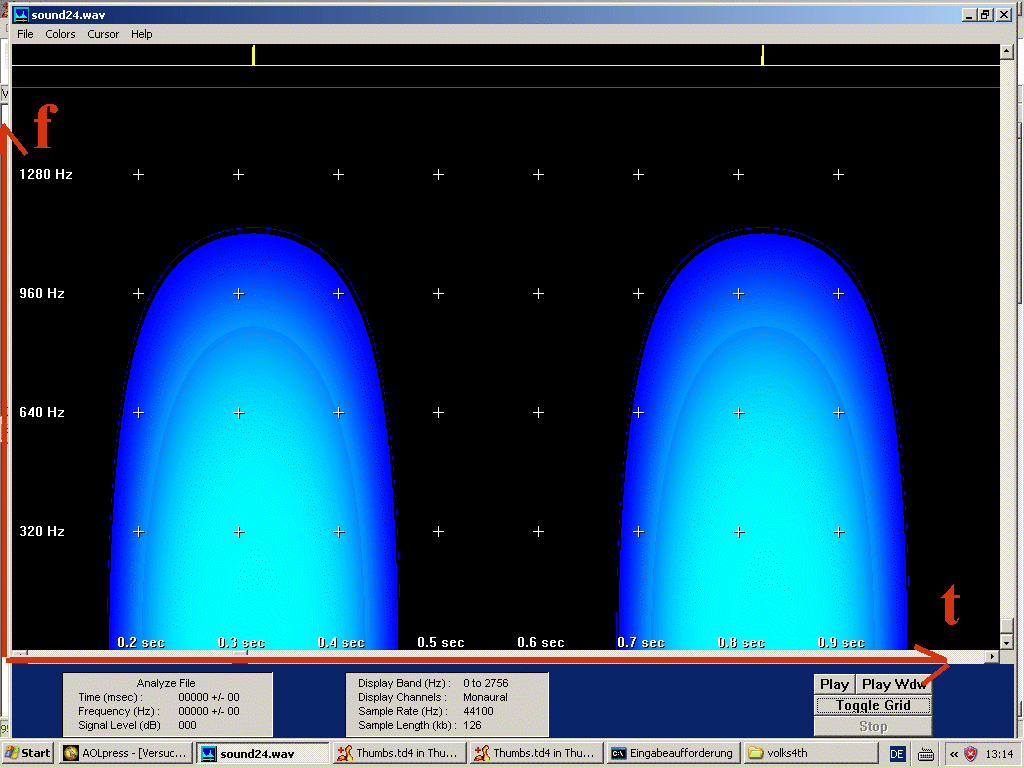
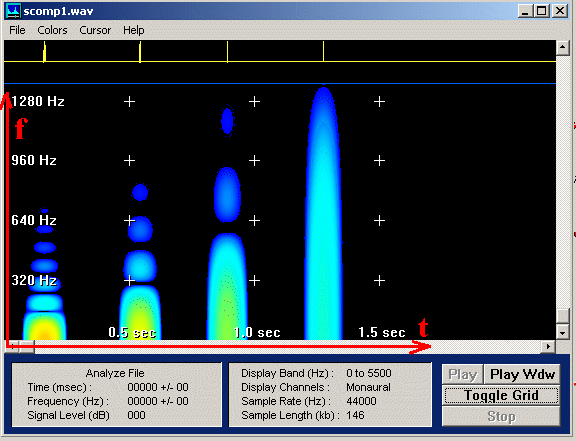
(1) Erzeugen Sie mit Ihrer Soundkarte und einem passsenden Programm (z.B. GOLDWAVE) einen Sinuston (z.B. 100 Hz) und schneiden Sie von ihm alles aus bis auf eine "Halbwelle" des Sinus. Wenn Sie sich das Geräusch anhören, werden Sie im Lautsprecher ein kurzes Knacken hören (auch eine Form eines Knalls). Sie können auch eine vorbereitete Sounddatei herunterladen. Später erzeugen Sie ein so genanntes Sonogramm (Sonagramm oder Spektrogramm), z.B. mit dem Programm GRAM.exe. Die Programme GOLDWAVE und GRAM können Sie kostenlos aus dem Internet herunterladen, zumindest in Erprobungsversionen.

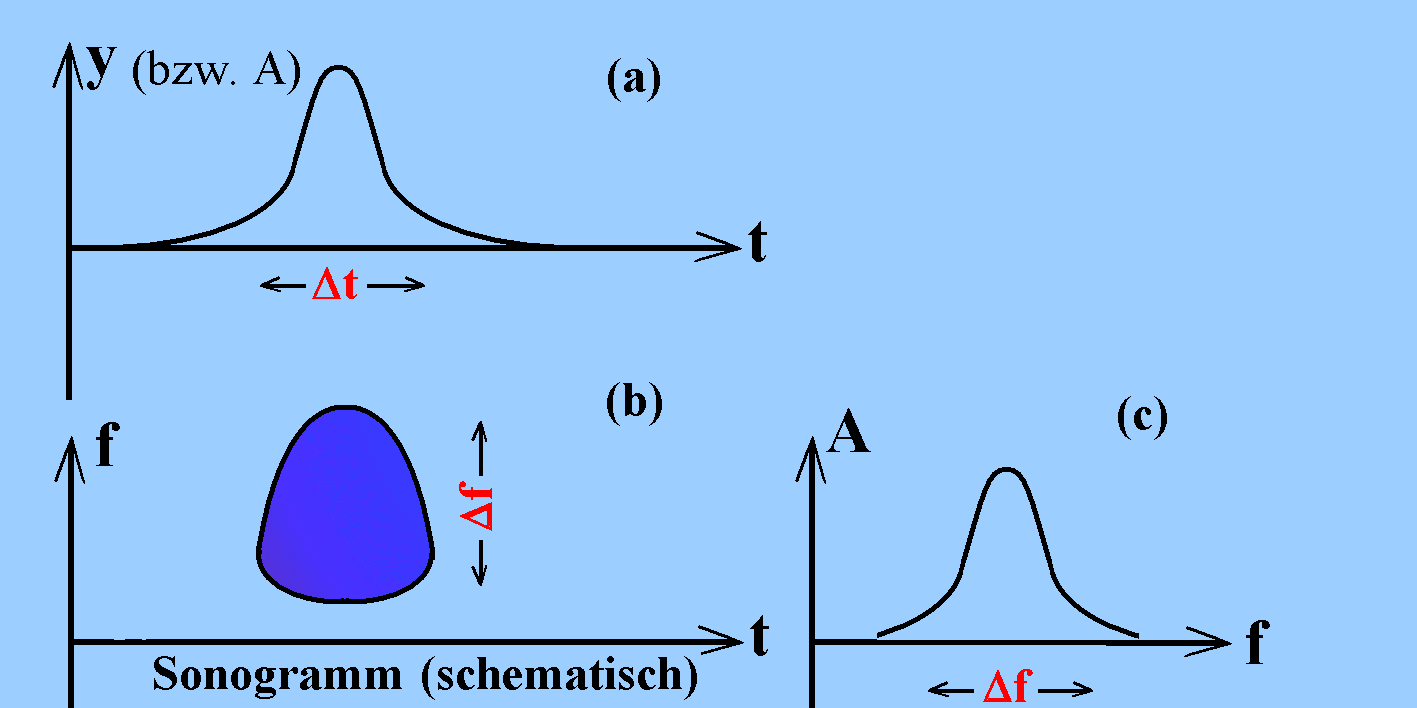
(2) Im obersten Diagramm (a) des nebenstehenden Bildes ist z.B. bei einem Knall der Druck y an einem bestimmten Ort in Abhängigkeit von der Zeit dargestellt. Darunter (b) ist der Bereich der beteiligten Frequenzen Df  in Abhängigkeit von der Zeit t dargestellt, ein so genanntes Sonogramm. 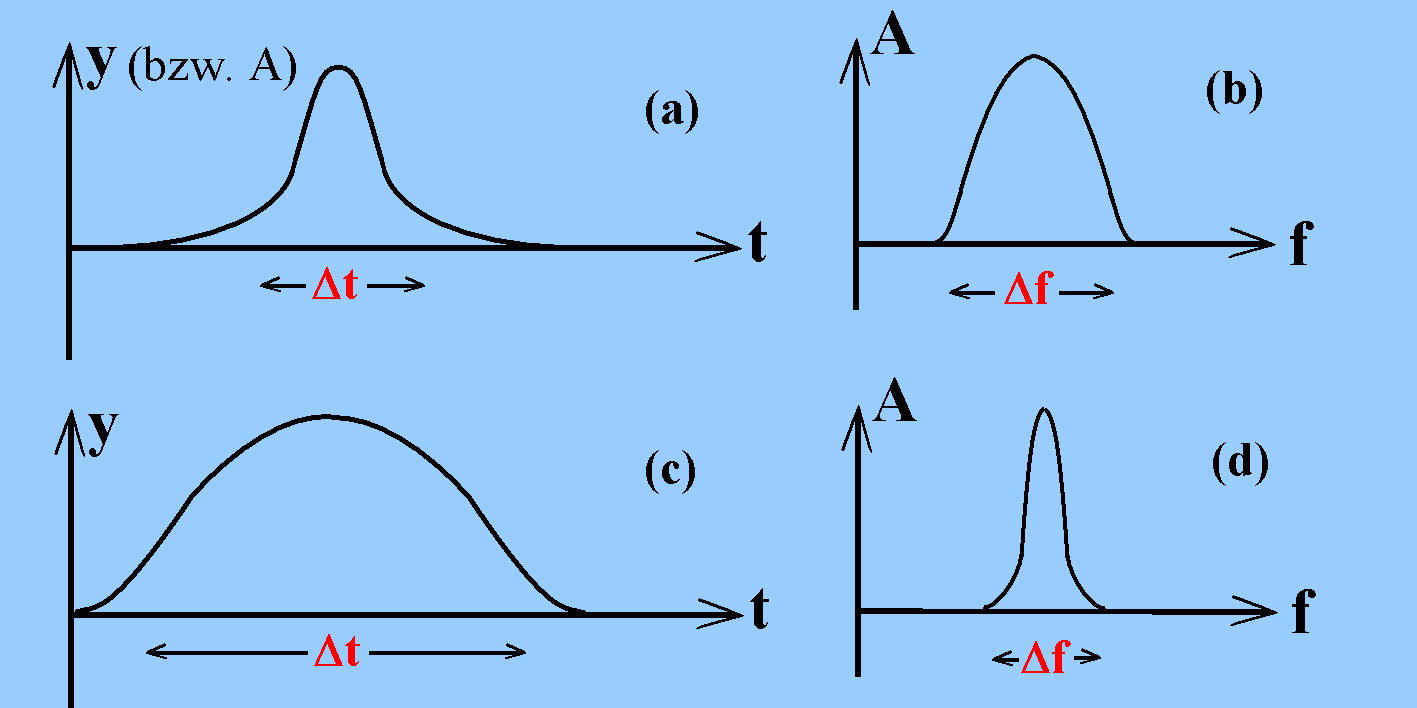(In der schematischen Zeichnung sind Informationen über die Amplituden der beitragenden Frequenzanteile weggelassen.) Rechts daneben (c) ist dargestellt, wie die Amplitude des jeweiligen Frequenzanteils im Knall von der Frequenz abhängt. In der Zeichnung werden eine "Zeitunschärfe" Dt und eine "Frequenzunschärfe" Df definiert.

b) Versuchsdurchführung:

(1) Erstellen Sie jetzt ein Sonogramm mit Hilfe eines geeigneten Programms, wie z.B.  GRAM.exe Mit GRAM erhalten Sie dann ein Bild ähnlich wie das Untenstehende (es zeigt die Analyse zweier "Knälle"):
	(2) Darstellung eines Sonogramms (Spektrogramms) von zwei Knallen: Nach rechts ist die Zeit aufgetragen, nach oben die Frequenz, durch die Farbe ist der Anteil der jeweiligen Frequenz bei der Überlagerung gekennzeichnet: Je "blauer", desto geringer ist der Anteil der jeweiligen Frequenz zur jeweiligen Zeit (kleine Amplitude A), je "gelber", desto größer ist der jeweilige Frequenzanteil (große Amplitude A). Sie sehen, dass bei diesem Knall Frequenzen bis ca. 1000 Hz beteiligt sind; der Hauptbeitrag liegt aber eher bei wenigen Hundert Hz. Es ist also ein ganzes Intervall von Frequenzen Df bei der Bildung bzw. Zerlegung eines Knalls beteiligt. Variieren Sie nun die Frequenz des anfänglichen Sinus, aus dem Sie einen Knall ausschneiden. Wenn alles gut geht, werden Sie folgendes beobachten: (Die Parametereinstellungen beim Programm GRAM erfahren Sie hier.)
	Sonogramme von mehreren Knallen (übereinander kopiert in einen Sound): Die Knalle wurden erzeugt aus Sinuskurven zu den Frequenzen 50 Hz, 100 Hz, 200 Hz und 500 Hz. Nach oben sind die jeweiligen Frequenzanteile aufgetragen, nach rechts die Zeit t. Je blauer (gelber) der jeweilige Frequenzanteil gezeichnet ist, desto schwächer (stärker) ist er. Je kürzer der Knall, zu desto höheren Frequenzen reicht das Frequenzspektrum.

c) Ergebnis:

E	Je kürzer die Zeitdauer des Knalls Dt, desto höhere Frequenzen sind beteiligt, desto größer ist das Intervall Df der beteiligten Frequenzen.

Schematisch soll das in den nebenstehenden Zeichnungen dargestellt sein. Die Zeichnungen (schematisch) zeigen Bemerkenswertes: In ihnen ist der Zeitverlauf des Knalls dargestellt [y(t),  Zeichnungen (a),(c)] und die beteiligten Amplituden A in Abhängigkeit von der Frequenz f, [A(f), Zeichnungen (b),(d)] für zwei verschieden lang andauernde Knalle. Frequenzanteile mit der Amplitude 0 kommen in den Knallen der Zeichnung nicht vor. Hauptbeitrag zum Knall kommt von solchen Frequenzen, bei denen die Amplitude A maximal ist. Zeitdauer Dt des Knalls und Breite der Frequenzverteilung Df  hängen miteinander zusammen:

E	1. Kurze Zeitdauer Dt bedingt große Breite der Frequenzverteilung Df . 2. Große Zeitdauer Dt bedingt geringe Breite der Frequenzverteilung Df .

Hinweis: Das Spektrogramm wird mit einer so genannten Kurzzeit-Fourier-Transformation erzeugt. Diese ist sehr verwandt mit der eigentlich einzusetzenden normalen Fourier-Transformation. Man wird also damit rechnen müssen, dass in bestimmten Fällen das Spektrogramm sich vom Ergebnis einer normalen FT unterscheidet.