 |
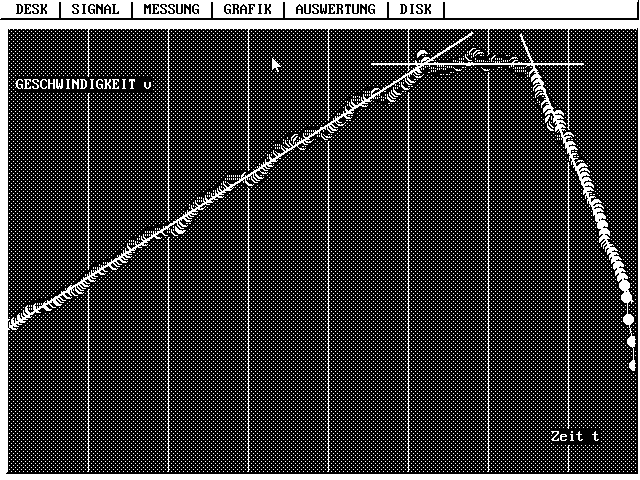
| Anfahr-, Ausroll- und Abbremsvorgang mit einem
Fahrrad:
Man erkennt deutlich den (fast) linearen Anstieg der Geschwindigkeit, annähernde Konstanz, und dann fast linearen Abfall der Geschwindigkeit. |
©
Horst Hübel Würzburg 2005 - 2014
|
Bewegungen unter dem
Einfluss einer konstanten Kraft; die Beschleunigung
|
In diesem Stadium ist bereits das Trägheitsprinzip besprochen bzw. das Trägheitsgesetz, das die Basis einer qualitativen Definition der Kraft ist (1. NG: Kraft ist die Ursache einer Beschleunigung (incl. Richtungsänderung)). Solche Beschleunigungen sollen jetzt für den Spezialfall einer konstanten Kraft untersucht werden. Von Prof. Heuer habe ich hierzu einen Realversuch kennen gelernt, der hier in abgewandelter Form wiedergegeben wird:
Ein Fahrrad soll mit "möglichst konstanter Kraft" beschleunigt werden. Als Fahrtenschreiber wird ein Kassettenrekorder verwendet, der über eine Schutzschaltung aus zwei antiparallelen Si-Dioden an den Fahrrad-Dynamo angeschlossen war. Je schneller sich das Rad dreht, desto größer ist die Frequenz des vom Dynamo erzeugten Wechselstroms. Ein Schüler soll (im Schnellgang) möglichst gleichmäßig tretend anfahren.
Anschließend hören sich die Schüler die Kassette an und beurteilen die Bewegung. Mittels der Tonhöhe können die Schüler spontan Schnellerwerden und Abbremsen beschreiben. Dann wird die Kassette in den Rechner eingespielt mittels eines Programms, das die Periodendauer misst (FAHRRAD), oder ein Sound-Programm wie WAVESTUDIO, GOLDWAVE etc., oder ein Sound-Programm wie GRAM, das eine Frequenzanalyse durchführte (Vgl. Buch "Schülerversuche mit PC ... ). Auch mit dem Sonarmeter ist ein ähnlicher Versuch möglich. FAHRRAD produziert z.B. auf dem Bildschirm folgende Graphik:
 |
| Anfahr-, Ausroll- und Abbremsvorgang mit einem
Fahrrad:
Man erkennt deutlich den (fast) linearen Anstieg der Geschwindigkeit, annähernde Konstanz, und dann fast linearen Abfall der Geschwindigkeit. |
Bemerkenswert sind folgende Beobachtungen der Schüler:
Damit ist der enge Zusammenhang zwischen Kraft und Geschwindigkeitsänderung schon recht gefestigt. Ein idealisiertes Experiment auf der Luftkissenfahrbahn bestätigt die Vermutungen:
Als konstante Kraft wird die konstante Hangabtriebskraft bei einer geneigten Fahrbahn genommen. Das ist ein besonders lehrer- (und schüler-) freundlicher Versuch, weil er keinerlei Justierarbeiten erfordert; sogar der exakte Startzeitpunkt kann durch optische und akustische Signale des Programms (z.B. VTLICHT) mühelos optimiert werden. Mit Lichtschranken wird die Geschwindigkeit beim Unterbrechen einer zweiten Lichtschranke in Abhängigkeit von der Laufzeit von der ersten zur zweiten Lichtschranke gemessen (das Programm korrigiert nach Wunsch automatisch auf die Gleitermitte: Zeitmittengeschwindigkeit). Es ergibt sich folgendes Bildschirmbild (Vgl. Erläuterungen im Buch "Physikalische Schülerversuche mit PC ... "):
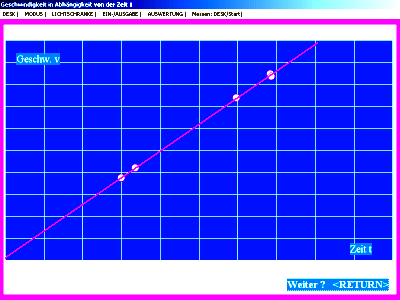 |
| Versuch mit zwei Lichtschranken an der
geneigten Fahrbahn (Momentangeschwindigkeit als Zeitmittengeschwindigkeit
gemessen):
Es ergibt sich eine fast perfekte Ursprungsgerade für das t-v-Diagramm: Die Geschwindigkeit v ist bei konstanter Kraft (hier Hangabtriebskraft) proportional zur Zeit. |
Ein entsprechender Schülerversuch ist auch durch Handstoppen an einer geneigten Kugelrinne mit dem Programm GALILEI möglich, bei dem die Schüler durch Tastendruck an der PC-Tastatur die Zeiten messen, zu denen eine Kugel an vorgegebenen Marken vorbei kommt. Auch hier ist das Ergebnis sehr überzeugend, wie das Bildschirmfoto zeigt:
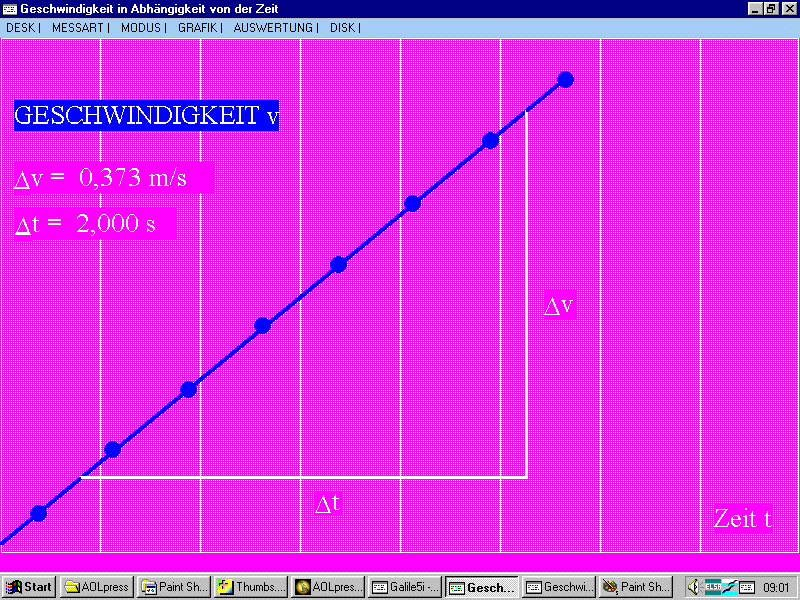 |
| Handstopp-Versuch an der geneigten
Kugelrinne mit PC-Programm GALILEI:
Auch hier ergibt sich eine fast perfekte Ursprungsgerade für das t-v-Diagramm: Die Geschwindigkeit v ist bei konstanter Kraft (hier Hangabtriebskraft) proportional zur Zeit. (Es ist auch ein mitlaufendes Steigungsdreieck vom Programm eingezeichnet, aus dem der Schüler direkt im Kopf die Beschleunigung ausrechnen kann, wenn der Beschleunigungsbegriff bereits bekannt ist. Dies ist also eine (genaue) Messung der Beschleunigung im Schülerversuch, die den Vorteil hat, dass sie auf die Definition der Beschleunigung zurückgreift.) (Vgl. Erläuterungen im Buch "Physikalische Schülerversuche mit PC ... ") |
Didaktischer Vorteil beider Versuche ist, dass die Sch die punktweise Entstehung eines Graphen miterleben, um so das "Denken in Graphen" zu erlernen.
Die Schüler stellen fest:
|
Bei konstanter Kraft verändert sich die Geschwindigkeit linear ("gleichmäßig"), mit konstanter Steigung. |
Die Steigung des t-v-Diagramms hat offenbar besondere Bedeutung. Die Steigung ist (wie immer bei einer Geraden) Δv /Δt. Sie ist ein Maß für die Geschwindigkeitsänderung Δv im Zeitintervall Δt und gibt die Geschwindigkeitsänderung pro Zeiteinheit an. Sie erhält einen besonderen Namen: Beschleunigung.
|
Definition: |
Beschleunigung a : = Δv/Δt . Sie ist ein Maß für die Geschwindigkeitsänderung pro Zeiteinheit. |
|
Versuchsergebnis: |
Bei einer konstanten Kraft F (hier Hangabtriebskraft) ist die Beschleunigung a konstant. |
Wichtig ist hier also der enge Zusammenhang zwischen Kraft und Beschleunigung.
Jetzt muss der Beschleunigungsbegriff noch griffig gemacht werden. Dazu lösen die Schüler einfache Kopfrechenaufgaben über den Zusammenhang von Beschleunigung a und Geschwindigkeitsänderung Δv = a ·Δt in einem bestimmten Zeitintervall Δt.
Der Weg von der Beschleunigung a zur Geschwindigkeit v entspricht damit wieder einem Flächenverfahren
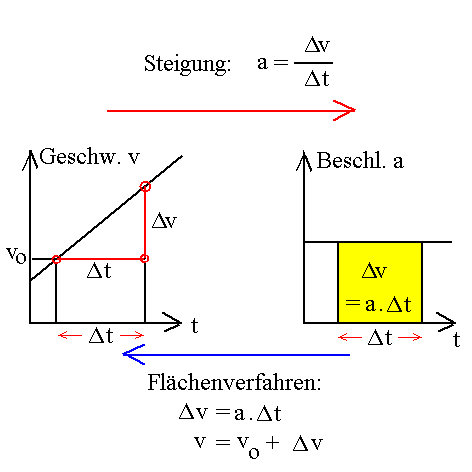 |
Von der Geschwindigkeit zur Beschleunigung durch die Steigung;
von der Beschleunigung zur Geschwindigkeit durch das Flächenverfahren.
Dabei ist v0 die Anfangsgeschwindigkeit zu Beginn des Zeitintervalls Δt.
Ganz entsprechend gelangte man bei der gleichförmigen Bewegung von der Geschwindigkeit zum Ort durch das Flächenverfahren. |
Geht das bei der gleichmäßig beschleunigten Bewegung immer noch?
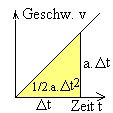 |
. | Versuchsweise wird die Fläche unter dem
t-v-Graphen berechnet:
Zunächst ergibt sich für die einfache Anfangsbedingung v0 = 0: ½·a·Δt2 bzw. ½·a·t2 Ist das t-x-Gesetz (also x = ½·a·t2 ) wirklich dementsprechend eine quadratische Gesetzmäßigkeit? |
Ein Fahrbahnversuch an der geneigten Fahrbahn mit konstanter Beschleunigung durch die Hangabtriebskraft bestätigt das.
| Δx = ½·a·Δt2 und x = x0 + Δx |
|
also:
x = x0 + ½·a·Δt2
|
Ein entsprechender Versuch kann z.B. durch Handstoppen mit dem Programm GALILEI durchgeführt werden. Hier erhält endlich das t-x-Diagramm seine Bedeutung. Dass das Flächenverfahren auch in diesem Fall die richtige Gesetzmäßigkeit liefert, wird als Bestätigung des Flächenverfahrens auch für diese Situation angesehen. Ohne weitere Überprüfung wird dann das Flächenverfahren für allgemeine Anfangsbedingungen angewendet:
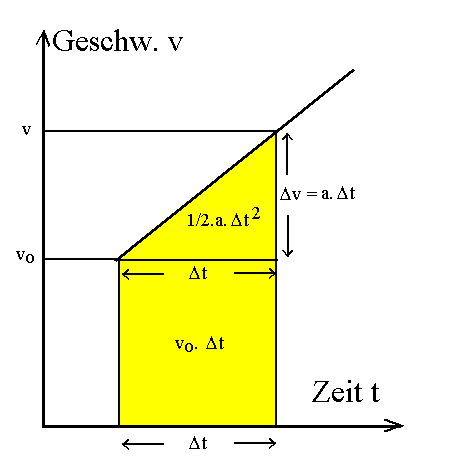 |
Es ergibt sich
Δx = v0.Δt + ½·a·Δt2 und mit dem Anfangsort x0 zu Beginn des Zeitintervalls Δt: x = x0 + Δx also:
x = x0 + v0·Δt + ½·a·Δt2 |
Ein leicht merkbares Schema wird manchmal auch "Prinzip der Unabhängigkeit der Bewegungen (PUB)" genannt:
|
|
Dabei ist v0 die Anfangsgeschwindigkeit
und x0 der (Anfangs-)Ort zu Beginn des jeweiligen
Zeitintervalls Δt. Dieser Satz von Beziehungen
gilt von jetzt ab als Grundgleichungen der Kinematik. Sie
sollten die Schüler im Bereich der Kinematik im Gedächtnis haben und
anwenden und keine anderen.
( Oktober 2024: geringe Ergänzungen)