Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig- keiten im Physik-UR An- schauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2014

2. Newtonsches Gesetz

Mittlerweile ist bekannt, dass eine Kraft definiert ist als Ursache für eine Beschleunigung. Durch ein Experiment soll nun der Zusammenhang zwischen Kraft und Beschleunigung aufgespürt werden.

Versuch: horizontale Fahrbahn, Antriebsgewichte über Faden und Umlenkrolle; die Gesamtmasse muss konstant bleiben, also Antriebsgewichte aus Vorrat auf dem Gleiter; auf dem Gleiter außerdem Reiter, der als Reflektor für die Ultraschall-Impulse des Sonarmeters dient; Steuer- und Auswertungsprogramm, z.B. SONAR. Durch den Trick, dass der ganze Vorrat der Antriebsmassen auf dem Gleiter mitfährt, kann man die Bedingung der konstanten Gesamtmasse einhalten. Gemessen werden Geschwindigkeiten in Abhängigkeit von der Zeit.^*)

Für unterschiedliche Antriebsgewichte werden die wachsenden Geschwindigkeiten der Bewegungen registriert und auf dem Bildschirm dargestellt. Die Beschleunigung erhält man unmittelbar als Steigung der t-v-Graphen, entsprechend ihrer Definition. (SONAR besitzt die Möglichkeit, ein Steigungsdreieck einzuzeichnen und die Steigung unmittelbar abzulesen.)

Weil nur Geschwindigkeitsmessungen durchgeführt werden, kommt es auf den Koordinatenursprung nicht an. Der einzige Justieraufwand, der durch das Sonarmeter auch noch vereinfacht wird,  besteht in der horizontalen Ausrichtung der Fahrbahn. Das kann sogar vor der Klasse geschehen.

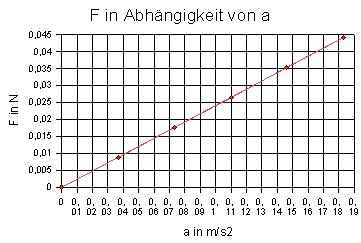
Das a-F-Diagramm zeigt sehr überzeugend die direkte Proportionalität. Die Proportionalitätskonstante stimmt recht gut mit dem Zahlenwert der Gesamtmasse überein: Identifizierung als Gesamtmasse m.

^*) Die Theorie des Versuchs ist einfach: Ein (etwas kompliziert aufgebauter) Körper mit einer Gesamtmasse m wird beschleunigt. Alle seine Teile (Wagen/Gleiter und Antriebskörper) werden in gleicher Weise beschleunigt. Es ist eine einzige Kraft als Ursache der Beschleunigung zu betrachten: die Gewichtskraft auf den Antriebskörper der Masse Δm. Reibung und "innere" Kräfte sind zu vernachlässigen.

Diese wohl eleganteste experimentelle Herleitung des 2. NG besticht durch ihre Präzision, ihre methodische Klarheit und durch die Tatsache, dass die Beschleunigung nicht über eine quadratische Gleichung gewonnen wird, sondern direkt von ihrer Bedeutung als Steigung des t-v-Graphen her.  Hinweise: möglichst leichter Faden (Seide); Horizontaljustierung, kontrolliert durch t-v-Diagramm bei gleichförmiger Bewegung; konstante Gesamtmasse, erreicht durch Umlegen bereits aufgefädelter Antriebsmassen (Holz-Perlen); durch den Trick des Auffädelns vermeidet man, dass die Antriebsmassen beim Aufprall jedesmal von ihrem Träger springen.

Messergebnis: Hier wurden vor der Messung die Zeit und die Schallgeschwindigkeit mit den entsprechenden Optionen des Programms SONAR kalibriert. Bei einer Gesamtmasse von 0,2385 kg ergab sich eine Steigung der Ausgleichsgeraden von 0,242 Ns²/m. Die Übereinstimmung ist beeindruckend! Statt, wie früher üblich, hier eine Proportionalitäts-Konstante c (F = c.m.a) einzuführen, die als 1 definiert wird, genügt es bei der vorliegenden hohen Präzision, die Schüler auf die Definition von 1 N hinzuweisen. ("1 kg in 1s aus der Ruhe auf 1 m/s durch die Kraft 1 N"), die festlegt, dass 1 Ns²/m = 1 kg.

Die geringfügige Abweichung von ca. 4 g könnte durch das Trägheitsmoment der Schnurrolle bedingt sein, die einer effektiven Zusatz-Masse entspricht. Dafür spricht, dass auch bei größeren Gleitermassen ein Fehler von derselben absoluten Größe entsteht. Daten über die effektive Masse konnte ich bei der Herstellerfirma nicht erhalten. Andere Fehler sind auch denkbar.

Es wird dann formuliert:

2. NG: Jede Kraft F bewirkt bei einem Körper der Masse m eine Beschleunigung a, die sich aus  F = m.a ergibt.

Also:  Die Kraft F hat eine Beschleunigung zur Folge, und diese ist proportional zur Kraft. Die Proportionalitätskonstante ist gerade die Masse m des beschleunigten Körpers. Wenn die Kraft konstant ist, ist es auch die Beschleunigung. Eine solche Bewegung nennt man gleichmäßig beschleunigte Bewegung.

Dann muss ein scheinbarer Widerspruch zur Erfahrung diskutiert werden: Bei einer Autofahrt auf der geradlinigen, horizontalen Autobahn mit Höchstgeschwindigkeit weiß man, dass die Geschwindigkeit konstant ist und die Antriebskraft gerade maximal. Dennoch also Beschleunigung a = 0?

Konstante Maximalgeschwindigkeit, weil insgesamt keine Kraft auf den PKW wirkt: die maximale Antriebskraft wird aufgehoben durch die ebenfalls maximale Reibungskraft. Es ist die Gesamtkraft F, die in das 2. NG eingeht!

Ein entsprechender Versuch lässt sich auch mit Schülerversuchs-Fahrbahnen und einem IR-Bewegungsmesswandler mit demselben Programm SONAR durchführen. Die Genauigkeit des Faktors F/a hängt dann aber von der Kalibrierung der Entfernungsmessung ab. (Vgl. Buch Schülerversuche mit PC und ... )

Auch durch Handstoppen von rollenden Kugeln auf einer geneigten Kugelrinne mit dem Zeitmessprogramm GALILEI (Vgl. Buch Schülerversuche mit PC und ... ) kann man die Proportionalität zwischen F und a bei geringsten Kosten nachweisen. Durch unterschiedliche Bahnneigung wird eine unterschiedliche Hangabtriebskraft eingestellt. Das Auswertungsverfahren ist identisch. Im Proportionalitätsfaktor ist hier die Masse nur indirekt enthalten, direkter das Trägheitsmoment der rollenden Kugel bzgl. der Auflagepunkte.

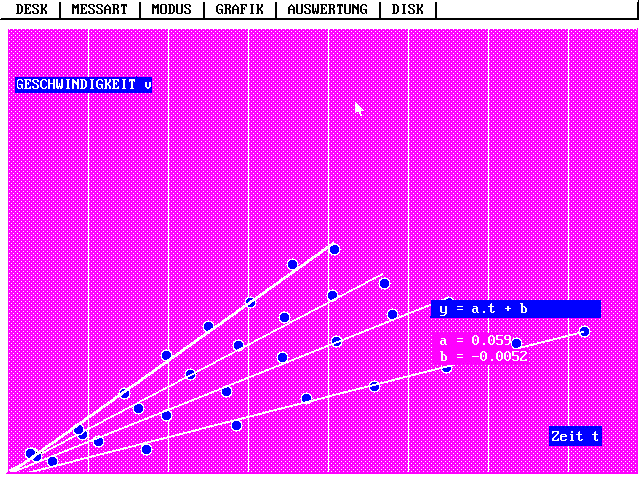
Handstopp-Versuch an der geneigten Kugelrinne mit PC-Programm GALILEI. Vgl. Buch "Physikalische Schülerversuche mit PC ... "): Man erkennt die Kugelrinne (U-förmige Aluschiene aus dem Baumarkt) mit Marken. Beim Vorbeirollen einer Kugel an einer Marke drückt einer der Schüler eine Maustaste des PCs (dem PC wurden vorher die Positionen der Marken mitgeteilt). Die Bahnneigung der Kugelrinne wurde in gleichen Schritten geändert, indem jeweils 2 Diagläser mehr am Startende untergelegt wurden. GALILEI misst mit Hilfe der Zeitmittenmethode Momentangeschwindigkeiten. Auch hier ergibt sich eine fast perfekte Ursprungsgerade für das t-v-Diagramm: Die Geschwindigkeit v ist bei konstanter Kraft (hier Hangabtriebskraft) proportional zur Zeit.

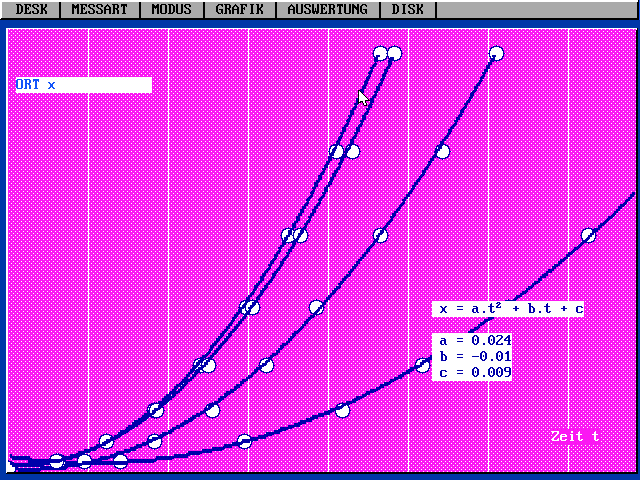
Handstopp-Versuch an der geneigten Kugelrinne mit PC-Programm GALILEI Vgl. Buch "Schülerversuche mit PC ... "): Die Steigung der Geraden (also die Beschleunigung a) lässt sich jeweils mit einem vom Programm eingezeichneten mitlaufenden Steigungsdreieck im Kopf berechnen. In der im Bild eingezeichneten Programm-Option wird eine Ausgleichsgerade eingezeichnet und die Steigung a ausgegeben. In der Zeichnung ist auch ein typischer Fehler demonstiert: bei der letzten Geraden wurde der Kugel beim Start offenbar ein kleiner Stoß in Gegenrichtung versetzt, der die "Anfangsgeschwindigkeit" geringfügig negativ machte. Der Fehler wirkt sich außer in der Graphik nirgendwo aus. Schon im Diagramm ist erkennbar, dass die Beschleunigung mit der Hangabtriebskraft wächst. Ein a-F-Graph mit den Daten der Abbildung ergibt eine recht überzeugende Ursprungsgerade:  F prop. a

Handstopp-Versuch an der geneigten Kugelrinne mit PC-Programm GALILEI: Nur der Vollständigkeit halber wird hier auch das t-x-Diagramm gezeigt. Durch die Ausgleichsparabeln würde man auch hier den Startfehler aus der Beschleunigungsmessung eliminieren. Das t-x-Diagramm ist für sich interessant. Bei der erstmaligen Einführung und der Ermittlung der Beschleunigung würde ich es aber vermeiden.

Die Bedeutung des 2. Newtonschen Gesetzes liegt darin, dass es erlaubt, bei bekannten Anfangsbedingungen (x₀ und v₀) Bewegungen vorherzusagen für alle Zeiten, für die die Kraft (Gesamtkraft) bekannt ist. Hier wird es wichtig, dass der komplette Satz von Anfangsbedingungen vorgegeben wird! Die Aussage:

heißt in der Physik Kausalität.

Der Freie Fall ist solch ein Beispiel:

Traditionell wird ein Experiment zum Freien Fall genutzt, um die Fallbeschleunigung zu messen. Man kann aus ihm aber eine ganze Menge mehr lernen. Mit Hilfe von Experimenten soll der Fall daher jetzt analysiert werden.

Sogar für Schülerversuche geeignet ist der Zackenkamm-Versuch, den ich 1983 durch von Dwingelo kennengelernt habe. Der so genannte Zackenkamm durchfällt eine Lichtschranke, und der PC stellt aus den Messdaten der Unterbrechungszeiten und bekannten Abständen der unterbrechenden Kanten ein t-x- oder ein t-v-Diagramm auf (z.B. das PC-Programm ZACKKAMM kann Momentangeschwindigkeiten nach der Zeitmittenmethode messen). Es handelt sich quasi um einen Freihand-Versuch, weil keinerlei Justierarbeiten nötig sind. Bewährt hat sich ein Zackenkamm aus Fotokarton mit einem Abstand von 3 cm zwischen jeder unterbrechenden (Unter-)Kante, der mit selbstklebender Folie flexibel gehalten wurde (beim Aufprall auf dem Boden sollte er keine Schäden davontragen). Mit einem Papiermesser lassen sich die Sprossen nach dem "Laminieren" leicht ausschneiden. Die freien Sprossen links wurden durch einen doppelseitigen Streifen Tesafilm stabilisiert, damit sie weniger flattern. Entsprechend dem Geschwindigkeitskonzept würde ich erst das t-v-Diagramm aufnehmen lassen. Es ergibt sich die perfekte Gerade der folgenden Abbildung:

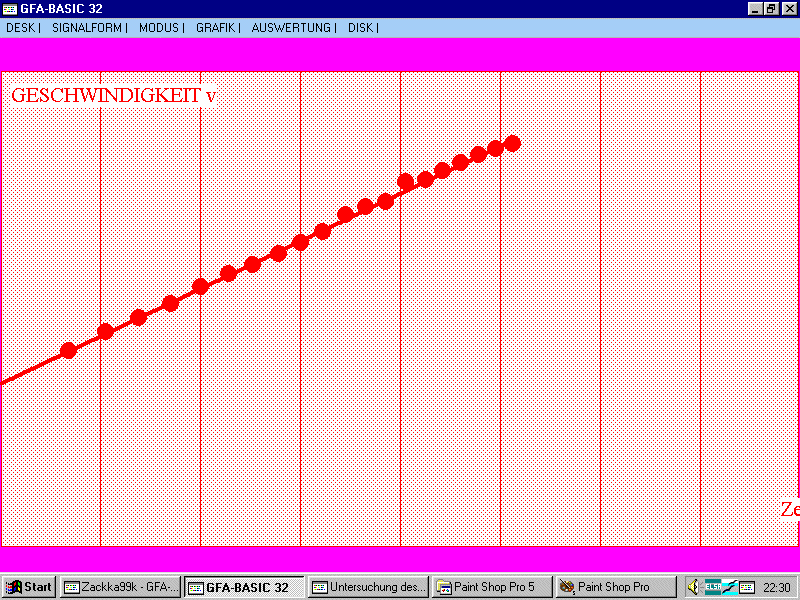Zackenkamm-Versuch mit einer Lichtschranke und dem Programm ZACKKAMM (Vgl. Buch "Schülerversuche mit PC ... "): An der fast perfekten Geraden für das t-v-Diagramm lässt sich viel zeigen, wie unten besprochen wird. Die Steigung der Geraden (also die Beschleunigung a) lässt sich jeweils mittels eines vom Programm eingezeichneten mitlaufenden Steigungsdreiecks  aus Dv / Dt  im Kopf berechnen.

Es ergeben sich eine Reihe von Fragen:

• Welche Art von Bewegung liegt vor? Antwort (A): gleichmäßig beschleunigte Bewegung mit konstanter Beschleunigung als Folge einer konstanten Kraft

• Um welche konstante Kraft handelt es sich? A: Gewichtskraft, die auf den Zackenkamm wirkt

• Was ändert sich, wenn aus einer größeren Höhe gestartet wird? A: parallelverschobene Gerade mit einer anderen Anfangsgeschwindigkeit v₀ (beim ersten Unterbrechen der Lichtschranke), die von der Starthöhe abhängt. Kein Einfluss auf die Beschleunigung bzw. Kraft!

• Was ändert sich, wenn durch eine aufgeklebte Münze die Masse des Zackenkamms vergrößert wird? In Deutschland sagen die Schüler dann meistens voraus, dass der Zackenkamm "schneller fallen" muss, weil sich die Erdanziehungskraft vergrößert hat.

  Das Versuchsergebnis - unveränderte Fallbeschleunigung - veranlasst die Schüler zur Vermutung, dass zwar die Gewichtskraft größer geworden ist, im 2. NG aber auch die Trägheit (Masse m). Das 2. NG zeigt mit Hilfe einer kleinen Rechnung, dass die Vermutung richtig ist.

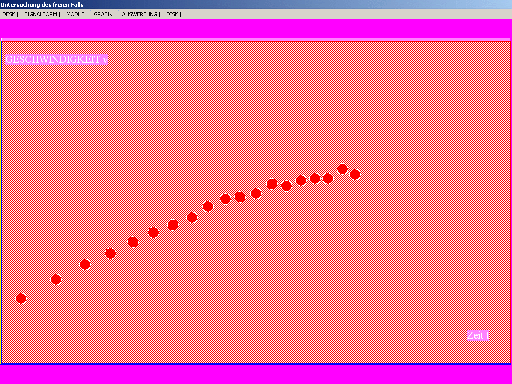
  Zackenkamm mit "Fallschirm"	t-v-Diagramm bei Fall mit Fallschirm. An der abnehmenden Steigung erkennen die Sch, dass die wirkende Kraft abnimmt. Sie deuten das als teilweise Aufhebung der Gewichtskraft durch die zunehmende Luftreibungskraft.

• Welchen Einfluss hat die Luftreibung? A: Im Experiment offenbar wenig. Man könnte die Luftreibung aber drastisch erhöhen, wenn man den Zackenkamm an einen Fallschirm hängt, der aus einem Taschentuch geknotet wurde. Wenn es gelingt, den Zackenkamm dann noch ohne Taumeln durch die Lichtschranke fallen zu lassen, bemerkt man, dass der t-v-Graph bei größeren Zeiten immer flacher verläuft: die Beschleunigung wird mit zunehmender Zeit kleiner.

• Ursache davon? A: Die Gesamtkraft auf den Zackenkamm nimmt im Laufe des Falls ab. Es wird erarbeitet, dass Gewichtskraft und Luftreibungskraft entgegengesetzt gerichtet sind. Je größer die Geschwindigkeit, desto größer der Betrag der Luftreibungskraft, desto kleiner die Differenz beider Kräfte.

• Wie groß ist die Fallbeschleunigung g? Man erhält i.A. recht genaue Werte für g. Das Ergebnis variiert u.U. leicht um den bekannten Wert. Gründe für eventuelle Abweichungen liegen darin, dass es in seltenen Fällen nicht gelingt, den Zackenkamm ohne Verkanten und Schlingern durch die Lichtschranke fallen zu lassen. Es sind keinerlei Justierarbeiten erforderlich.

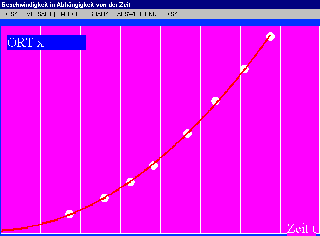
Natürlich bekommt man  mit dem Zackenkamm-Versuch auch wieder eine perfekte Parabel für das t-x-Diagramm. M.E. ist aber das t-x-Diagramm weniger ergiebig.

Vergleicht man die Vorhersagen Galileis und von Aristoteles zum Fall, muss man zur Kenntnis nehmen, dass sich nicht etwa einer der beiden geirrt hat. Vielmehr beschrieb Aristoteles einen Fall unter dem Einfluss starker Luftreibung, und Galilei einen Fall mit vernachlässigbarer Luftreibung. Bekanntlich fand der Test vom Schiefen Turm in Pisa durch Galilei nicht statt. Es wird behauptet, dass er eher in die Richtung von Aristoteles' Vorhersage gegangen wäre, wenn er durchgeführt worden wäre.

Analog lassen sich auch andere Bewegungen incl. von Realbewegungen (anfahrendes Fahrrad, Moped, PKW, ... ) untersuchen, z.B. die Bewegung des im Buch Schülerversuche mit PC ... " beschriebenen Propellerfahrzeugs. Für Schülerversuche im Labor geeignete Methoden dazu sind Handstopp-Versuche oder Versuche mit dem IR-Bewegungssensor. Das Bild zeigt ein t-x-Diagramm für ein anfahrendes Propellerfahrzeug auf einer Fahrstrecke von ca.  1 m, aufgenommen durch Handstoppen. Die Gerade des entsprechend aufgenommenen t-v-Diagramms beweist das Vorliegen einer gleichmäßig beschleunigten Bewegung mit einer konstanten Antriebskraft.

Anmerkung: Auch aus dem t-x-Diagramm lässt sich bei einfachen idealen Anfangsbedingungen (x₀ = 0, v₀ = 0) das Vorliegen einer Parabel beweisen, wenn das t-Öx-Diagramm aufgetragen wird. Dann sollte sich eine Ursprungsgerade ergeben.

Zackenkamm-Versuch mit einer Lichtschranke und dem Programm ZACKKAMM (Vgl. Buch "Schülerversuche mit PC ... "; Bildschirmfoto einer älteren Programm-Version): Die perfekte Gerade beweist die quadratische Gesetzmäßigkeit für das t-x-Diagramm. Zugleich wird gezeigt, wie mit dem zuschaltbaren mitlaufenden Steigungsdreieck die Steigung durch Kopfrechnen ermittelt werden kann. Für die Beschleunigung würde sich hier - wie man leicht nachrechnen kann - g = 9,78 m/s2 ergeben.