Physik-Versuch des Monats September/Oktober 2013: Wärme, innere Energie und Temperatur

Bisherige Versuche des Monats

Ziel: Die Schülerinnen und Schüler sollen bei einem Erwärmungsversuch eindringlich die begriffliche Verschiedenheit von zugeführter Energie/Wärme, innerer Energie und Temperatur erleben. Ihnen soll bewusst werden, dass die beteiligten Energien einen Mengencharakter besitzen (extensive Größen), nicht aber die Temperatur als Zustandsgröße (intensive Größe).

(1) Es bleibt trotz immensen Zuredens den Schülern erfahrungsgemäß unbegreiflich, dass in der Physik mit "Wärme" etwas anderes gemeint ist als in der Umgangssprache. Das ist zwar kein physikalisches Problem, sondern ein rein semantisches. "Wärme" in der Physik ist halt anders definiert als in der Umgangssprache. Man hätte ihr auch einen ganz anderen Namen geben können. Wärme in der Physik wird als übertragene Energie definiert. Manchmal wird sie deshalb auch "Wärmearbeit" genannt.

Ein Erwärmungsversuch könnte noch einige Schüler mehr davon überzeugen, dass im physikalischen Sinn Wärme etwas total anderes ist als Temperatur. Üblicherweise werden Varianten des Versuchs im Unterricht durchgeführt. Die Schwierigkeit ist dabei, dass Wärme und Temperaturänderung zueinander proportional sind. Es besteht die Gefahr, dass für Sch der Unterschied zwischen beiden nur in einem Proportionalitätsfaktor besteht, dass beide doch "mehr oder weniger das Gleiche sind".

Der vorgeschlagene Versuch macht die Verschiedenartigkeit durch unterschiedliches Zeitverhalten augenfällig:

Über eine Vielfachsteckdose mit Netzschalter wird Wasser in einem Wasserkocher erwärmt. Es sollen jeweils gleiche Portionen von Wärme ΔQ an das Wasser übertragen werden. Dazu wird für eine bestimmte Einschaltdauer Δt die Portion von Wärme aus der bekannten Leistung des Wasserkochers erst einmal ausgerechnet, z.B. bei P = 1000 W und Δt = 20 s: ΔQ = 20 kJ.

Variante a) Es wird entschieden, z.B. 10 Wärmeportionen ΔQ zuzuführen. Dazu wird 10 x der Netzschalter für die festgelegte Zeit eingeschaltet. Erst, wenn dies geschehen ist, wird (nach einiger Zeit) die Temperaturänderung bestimmt. Die sich aus ihr ergebende Änderung der inneren Energie des Wassers wird berechnet und mit der zugeführten elektrischen Energie (von gleichem Betrag wie die Wärme) verglichen. Interpretation: Wärme ist übertragene Energie, die die innere Energie erhöht.

Variante b) Die einzelnen Wärmeportionen werden mit Zeitabständen zugeführt und mitgezählt. Ausgehend von einer fiktiven anfänglichen inneren Energie (z.B. 1 MJ) wird die jeweilige innere Energie (1 MJ + n·ΔQ; n = 1,2,3 ... ) in einer Wertetabelle registriert (Tabelle 1). Die innere Energie steigt in den festgelegten Schritten linear an (Punktediagramm). Kontinuierlich wird die Temperatur mitgemessen, z.B. mit einem PC, aber zunächst in eine andere Wertetabelle eingetragen (Tabelle 2). Die Temperatur steigt in "ausgewaschenen" Stufen an und zeigt an, dass sich mit der zunehmenden inneren Energie der "Wärmezustand" des Wassers verändert, also die Temperatur, aber eben anders als die innere Energie. Durch die Nummer der Wärmeportion lassen sich beide Tabellen vergleichen.

Interpretation:

Tabelle 1:  Wärme erhöht die innere Energie.

Tabelle 2: Das  ist verbunden mit einer sich ändernden Temperatur. Dass die Temperaturänderung so nachhinkt (die Wärme ist bereits zugeführt, aber erst allmählich stellt sich im ganzen System einheitliche Temperatur ein), demonstriert klar, dass zwischen Temperatur, zugeführter Wärme und innerer Energie nur ein indirekter Zusammenhang besteht.

Gut wäre es, den Versuch geeignet zu inszenieren, so dass klar wird, dass die Wärmeportionen nichts mit dem Wasser zu tun haben, sondern von der Außenwelt herkommen. Dazu könnten Schilder dienen ("Wärmeportion" beim Schalter; "Erhöhung der inneren Energie" beim Wasserkocher); ideal wäre es, wenn die jeweilige Nummer der Wärmeportion durch ein Messgerät angezeigt werden könnte. Das könnte ein PC sein, der mit einer vorgegebenen Einschaltdauer über ein Einschaltrelais den Stromfluss ermöglicht.

Wir haben auch gute Erfahrungen mit einem "Funkschaltgerät" gemacht, wo ein Schüler von seinem Platz aus in bestimmtem Rhythmus die Wärmezufuhr mit einem Handschalter (links) ein- und ausschalten konnte. Noch eindrucksvoller wird der Versuch, wenn drei Schülergruppen getrennte Versuche mit unterschiedlichen Einschaltdauern oder gleichen Einschaltdauern und unterschiedlich langen Pausen dazwischen durchführten (funkgesteuerte Steckdosen werden häufig im Dreierset angeboten). Das Funkschaltgerät hat auch noch den Vorteil, dass die Schüler vom Platz aus die Energiezufuhr steuern können und dort ungestört die Messergebnisse in Wertetabellen eintragen können. (z.B. Schüler A schaut auf seine Uhr und gibt alle 20 s ein Kommando, B bedient nach diesem Kommando den Funkschalter, C protokolliert die Nummer des Energiepakets und die jeweilige innere Energie; der PC registriert, z.B. alle Sekunden, die jeweilige Temperatur. Ein weiterer Schüler rührt das Wasser im Kocher kräftig um.)

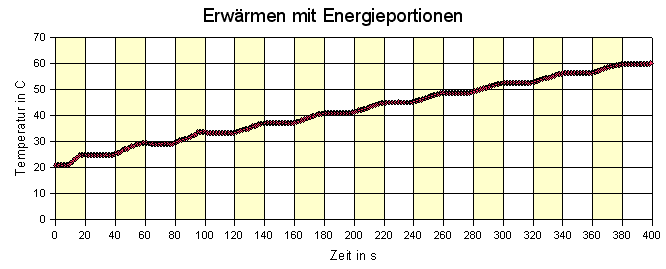	Hier wurde alle 20 s der Wasserkocher eingeschaltet, dann wurden 20 s zum Temperaturausgleich gegeben. Man erkennt schön, dass kein direkter Zusammenhang zwischen Wärmeportion und Temperatur besteht, dass es erst eine gewisse Zeit dauert, bis (u.a. als Folge des Rührens) thermisches Gleichgewicht entstanden ist, dass die Temperatur nur "im Wesentlichen" linear wächst. Ähnliche Kurven zeigen, welchen Einfluss es hat, wenn das Wasser im Kocher kräftig gerührt wurde. Gleiche Wärmezufuhr führt mit Sicherheit zur gleichen Zunahme der inneren Energie, aber nach dem Versuch auch zu einer konstanten Temperaturänderung, nachdem thermisches Gleichgewicht eingetreten ist. Bei 10 Wärmeportionen, P = 1000 W,  Δt = 20 s,  also ΔQ = 20 kJ ergibt sich bei m = 1 kg eine spezifische Wärmekapazität c = 20 kJ ·10 / (1 kg ·40 ºC) = 5 kJ/kgºC statt 4,18 kJ/kgºC.
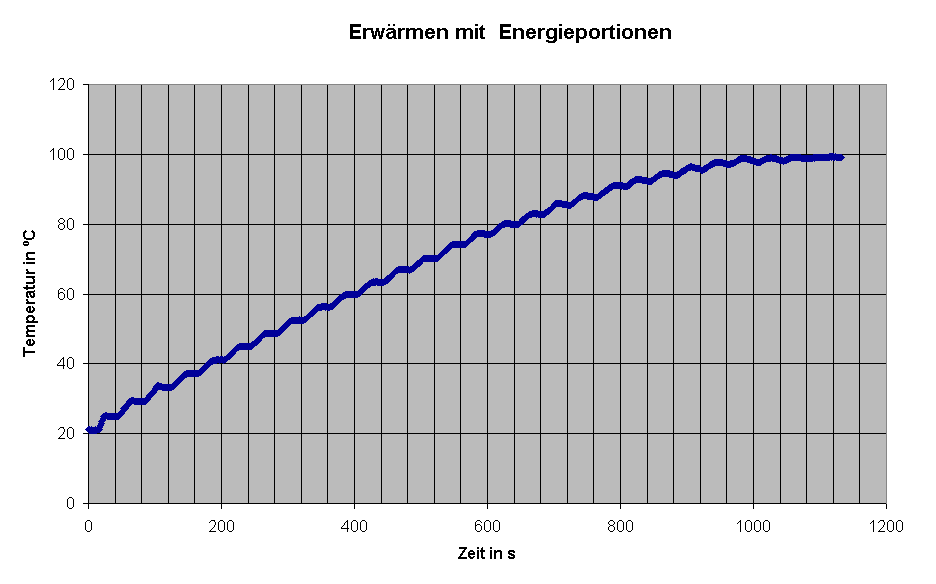
	Der relativ hohe Fehler hängt wohl mit Energieverlusten zusammen, die eine zu geringe Temperaturerhöhung ergeben, auch damit, dass die Wärmeaufnahme des Wasserkochers nicht berücksichtigt wurde. Bei höheren Temperaturen zeigt eine bis zur Siedetemperatur aufgenommene Kurve (links) in den Wartephasen sogar eine Temperaturabnahme wegen Energieverlusten nach außen.
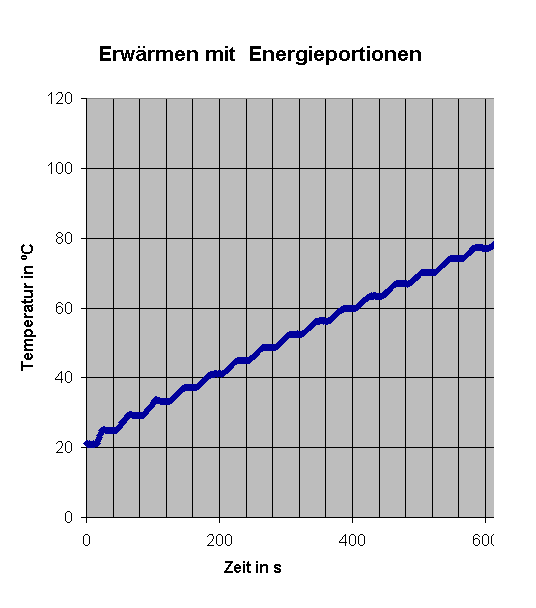	links Ausschnitt aus obigem Diagramm: Dagegen ist anfänglich das weitgehend "ideale" Verhalten deutlich erkennbar. Häufig wird man sich auf den linearen Bereich beschränken.

(2) Überlegung: Halbiert man die erwärmte Wassermenge, ist klar, dass die innere Energie mit halbiert wurde. Für beide Hälften wurde jeweils auch nur die halbe Wärme benötigt. Beide Hälften haben aber dieselbe Temperatur.

Folgerung:

Temperatur besitzt keinen Mengencharakter. Sie zeigt nur den "Wärmezustand" an (Betonung auf Zustand; besser wäre "thermischer Zustand").

(3) Es lässt sich die spezifische Wärmekapazität bestimmen. Unabhängig von Energieportion, Einschaltdauer, Wartezeit sollten alle Versuchsgruppen etwa den gleichen Wert erhalten, charakteristisch für Wasser. Das Ergebnis könnte durch die Energieaufnahme des Kochers und Energieverluste nach außen verfälscht sein. Es ist offensichtlich, wann die zu benutzende Temperaturdifferenz abgelesen werden sollte.