Geschwindigkeit als Steigung des t-x-Graphen

In der Didaktik wird zwischen Geschwindigkeit und Tempo unterschieden (vgl. didaktogene Lernschwierigkeiten), ähnlich wie im englischen Sprachraum zwischen velocity und speed unterschieden wird. In der Schulmechanik kann man eigentlich nur mit dem Geschwindigkeitsbegriff etwas anfangen.

Ausgangspunkt ist ein einfaches Experiment mit einer gleichförmigen Bewegung (Bewegung mit konstanter Geschwindigkeit). Beispiele:

• Schüler bringen auf dem Boden Marken an. An jeder Marke wird ein Schüler mit einer Stoppuhr aufgestellt. Ein Proband versucht möglichst mit konstanter Geschwindigkeit die Strecke zu durchlaufen, während der Rest der Klasse stoppt. Die Bewegung kann verglichen werden mit einer zweiten, bei der Proband erst anläuft und dann wieder langsamer wird.
• Im arbeitsgleichen Schülerversuch stoppt jede Schülergruppe die Bewegung einer Luftblase in einem langen wassergefüllt Rohr (man muss den Schülern klarmachen, dass sie immer die Zeit vom Start der Blase an registrieren müssen).
• Analog wird ein einmal angestoßener Gleiter auf der horizontalen Luftkissenfahrbahn, ein Motorwagen oder eine Spielzeug-Eisenbahn ausgestoppt.

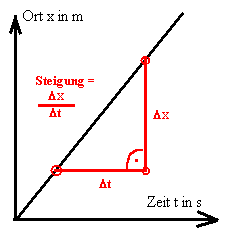
Die Schüler zeichnen ein t-x-Diagramm mit den Daten. Die Konstanz der Steigung ist Anlass, ihr einen Namen zu geben: Geschwindigkeit:

Geschwindigkeit:     v = Δx / Δt "Geschwindigkeit ist Ortsänderung pro Zeiteinheit"

"graphischer Steigungsbegriff"

Der Zusammenhang mit der Steigung des t-x-Graphen und die Folge der beiden möglichen Vorzeichen von v werden konkretisiert bei Realbewegungen vor dem Sonarmeter (indem z.B. eine Versuchsperson hin und her geht). Dabei kann ohnehin nicht vermieden werden, zwischendurch Bewegungsabschnitte mit nicht konstanter Geschwindigkeit zu betrachten. Wichtiger als ein Zusammenhang mit irgendwelchen Formulierungen des Differentialquotienten erscheint ein anschaulicher Zusammenhang mit so etwas wie "Steilheit" oder die Orientierung der Hand, die quasi parallel an den Graphen angelegt wird. Der Schüler muss ein Gefühl dafür bekommen, wie sich größere oder kleinere Geschwindigkeit im Anstieg oder Abfall des t-x-Graphen ausdrücken.

"manueller Steigungsbegriff"

.

Hinweis: Tempo (das der Autotacho anzeigt) wäre zu definieren als "Wegabschnitt pro Zeiteinheit". So wichtig der Begriff für Kraftfahrzeugtechnik und Verkehr ist, sowenig kann man in der Schulmechanik etwas mit ihm anfangen. "Weg durch Zeit" ist noch weniger brauchbar, da es nur für eine spezielle Anfangsbedingung gültig ist.

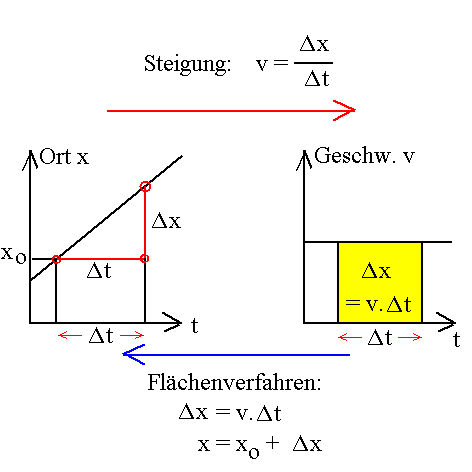Der Weg vom t-x-Diagramm zur Geschwindigkeit läuft über die Steigung. Es gibt auch einen Weg vom t-v-Diagramm zur Ortsänderung Δx = v · Δt: das "Flächenverfahren". Bei konstanter Geschwindigkeit entspricht die Ortsänderung Δx  in einem Zeitintervall Δt der Fläche unter dem t-v-Graphen. Von der Ortsänderung Δx kommt man zum Ort x, wenn man den Anfangsort x0 zu Beginn des Zeitintervalls hinzu addiert (Es handelt sich um eine "Integration". In der Schule nenne ich sie (zunächst) "Flächenverfahren"):      Δx = v · Δt      und       x = x0 + Δx   also:      x  = x0 + v · Δt Das gilt für ein beliebiges Zeitintervall Δt, wenn zu seinem Beginn der Ort x0 ist. Wenn das Zeitintervall Δt zur Zeit t = 0 beginnt, kann statt Δt auch t geschrieben werden.

Das Flächenverfahren stellt ein Vehikel dar, mit dem im Fall von beschleunigten Bewegungen vom t-a-Diagramm zum t-v-Diagramm und dann zum t-x-Diagramm fortgeschritten wird.

Bei "gestückelten" Bewegungen bzw. der "Methode der kleinen Schritte" ist dabei zu berücksichtigen, dass für jedes Intervall der im vorhergehenden Intervall erreichte Wert als Anfangswert eingeht. Kleine Fehler summieren sich deshalb.

Geschwindigkeitsmessung mit Lichtschranken: die Zeitmittengeschwindigkeit