© Horst Hübel Würzburg
2005 - 2014
Vorschlag von Dr. Matthias Krapf und Dr. Horst Hübel, Friedrich-Koenig-Gymnasium Würzburg Dies wird, zusammen mit der 10. Klasse, zukünftig nach dem überholten Lehrplan 2003 die einzige Stelle sein, in der die Beschleunigung behandelt wird. Laut ISB "würden wir Lehrer etwas falsch machen, wenn wir die Beschleunigung in der 10. Klasse noch einmal durchnehmen würden". Das heißt, die Beschleunigung muss in der 7. Klasse so durchgenommen werden,
Ich weiß nicht, wie sich die Lehrplan-Kommission das vorgestellt hat, aber ich gehe jetzt einmal davon aus, dass nicht jeder Aspekt von a behandelt werden soll.
Was verbleibt, ist eine operationale Einführung der Beschleunigung, ausgehend vom Schülerinteresse: 1. Beschleunigungsbegriff a) Frage aufwerfen: Ein Porsche "beschleunigt" in einer bestimmten Situation von 0 auf 96 km/h in 12 s, ein Fiat Punto von 0 auf 64 km/h in 8 s: Welches Fahrzeug "beschleunigt stärker"? Daraus wird auf "Geschwindigkeitsänderung pro Zeiteinheit" hingelenkt, also auf 96/12 km/h / s = 8 km/h / s bzw. auf 64/8 km/h / s = 8 km/h / s . Beide Fahrzeuge beschleunigen in der Situation gleich stark, "weil sie ihre Geschwindigkeit in 1 s um 8 km/h ändern. Der mögliche Schülerprotest, dass der Porsche doch stärker beschleunige, wird genutzt um darauf hin zu weisen, dass die tatsächliche Beschleunigung vom "Gas", also von der gewählten Antriebskraft, abhängt. b) Definition: Beschleunigung a soll "Geschwindigkeitsänderung pro Zeiteinheit" sein (ohne Artikel, da Beschleunigung keine Geschwindigkeitsänderung ist) . Die gemischten Einheiten werden bewusst gewählt, damit die Schüler das Zustandekommen der komplizierten Einheit für die Beschleunigung erkennen. Sobald das akzeptiert ist, kann zu m/s2 übergegangen werden, wenn nicht mehr die Gefahr besteht, dass die Schüler sich den Kopf zerbrechen, was "Quadratsekunden" sein sollen. Es wird anschaulich gemacht: Bei einer Beschleunigung 10 m/s2 erfolgt in 1 s eine Geschwindigkeitsänderung um 10 m/s, in 2 s um 20 m/s usw. c) Zahlenbeispiele in Form von Kopfrechenaufgaben machen den Begriff der Beschleunigung operational begreifbar: Jetzt ist die Geschwindigkeit 5 m/s; die Beschleunigung ist 2 m/s2. Wie groß ist dann die Geschwindigkeit dann nach 5 s? Klar: 5 m/s + 2 m/s2*5s = 15 m/s. Unter mehreren Beispielen sollten auch welche mit negativer Beschleunigung sein: Jetzt ist die Geschwindigkeit 10 m/s; wie groß ist die Geschwindigkeit 2 s später bei der Beschleunigung - 3 m/s2 ? Klar: 10 m/s - 3 m/s2*2s = 4 m/s. Jetzt ist das Fahrzeug unter dem Einfluss einer negativen Beschleunigung langsamer geworden; seine Geschwindigkeit hat abgenommen. Und auch: Jetzt ist die Geschwindigkeit - 10 m/s (Was bedeutet das negative Vorzeichen? Aha: Rückwärtsbewegung); wie groß ist die Geschwindigkeit 2 s später bei der Beschleunigung - 3 m/s2 ? Klar: -10 m/s - 3 m/s2*2s = - 16 m/s. Evtl.: Das Fahrzeug bewegt sich jetzt also schneller in negative Richtung; dennoch hat seine Geschwindigkeit abgenommen, wie es bei einer negativen Beschleunigung immer der Fall ist. Den letzten Punkt wird man in der 8. Klasse möglicherweise verschweigen. Nach einigen solchen Kopfrechenübungen sagen Ihnen die Schüler protestierend, dass sie die Beschleunigung verstanden haben. d) Sie werden dennoch Ihre Überraschungen erleben, wenn Sie in der nächsten Stunde einen Schüler zur Abfrage eines anderen Schülers beauftragen, ein geeignetes Zahlenbeispiel zum Beschleunigungsbegriff zu erfinden. Das ist nochmal schwerer als mit vorgegebenen Zahlenwerten eine Geschwindigkeitsänderung auszurechnen, sollte aber unseren Schülern zugemutet werden können, und ist heilsam für Schüler wie Lehrer, die dann mitbekommen, ob sie nur an die Klasse hingeredet haben. Selbst in der 11. Klasse schaffen das manche Schüler immer noch nicht. 2. Folgerung: t-v-Graph a) In der 11. Klasse hätte ein Experiment zur Aufnahme eines t-v-Diagramms am Anfang gestanden, z.B. mit Lichtschranken und durch Handstoppen an der Kugelrinne im Schülerversuch. Seine konstante Steigung hätte zur Definition der Beschleunigung als Steigung motiviert. In der 8. Klasse genügt es wohl, von der (vermeintlichen) Alltagserfahrung des Beschleunigens von PKWs auszugehen. Dann kann der t-v-Graph aus der Bedeutung der Beschleunigung erschlossen werden: (a = 2 m/s2 , Anfangsbedingung: v0 = 0 m/s): In der 1. Sekunde ändert sich die Geschwindigkeit um + 2 m/s auf 2 m/s, in der zweiten Sekunde wiederum um 2 m/s auf 4 m/s etc. So konstruieren die Schüler schrittweise den t-v-Graphen als Ursprungsgerade.
c) Dann werden für einen Überholvorgang mit konstanten Beschleunigungen die zwei Graphen rechts vorgegeben. Die Schüler sollen kreativ eine Story dazu erfinden mit Werten aus dem Diagramm (Gruppenarbeit). Z.B.: Gerade als die Ampel von rot auf grün umschaltet, wird ein an der Ampel stehender PKW A von einem PKW B überholt. Dieser hat beim Überholen die Geschwindigkeit 10 m/s. Nach 3 Sekunden haben beide PKWs die gleiche Geschwindigkeit 16 m/s. Ob alle Schüler es schaffen zu erkennen, dass hier kein 2. Überholvorgang beschrieben wird? In meiner 11. Klasse fielen immerhin 2 Schüler darauf herein. In meiner 11. Klasse wurde auch ein vertikaler Wurf nach unten vorgeschlagen. Die Anfangsgeschwindigkeit sollte erreicht werden, indem der Stein nach unten geworfen wird, während der andere aus der Ruhe startet. Heftige Diskussion entstand, als einige der Schüler die unterschiedliche Beschleunigung durch unterschiedliche Massen erklären wollten. Andere Schüler verbesserten und erklärten sie mit unterschiedlicher Luftreibung: Heftige Diskussionen, die Probleme aufgeworfen haben, die aber nur für einen Teil der Klasse gleich geklärt werden konnten. d) Der Graph soll jetzt gelesen werden: Wann etwa hat das anfangs schnellere Auto die doppelte Geschwindigkeit im Vergleich zum anderen? Wie groß sind die beiden Beschleunigungen? Welches Fahrzeug beschleunigt stärker? Wann ist das anfangs ruhende Fahrzeug doppelt so schnell wie das andere? i) Kreativ eine Story erfinden: Wie könnten die Graphen weiter verlaufen, was passiert entsprechend dieser Fortsetzung des Graphen? Hier sind alle Möglichkeiten offen. Indem die Schüler sich für eine Möglichkeit entscheiden, klären sie diese eine Situation. Die vielen Varianten in der Klasse führen zu heftigen Diskussionen.
In der 11. Klasse könnte man sich einfache Graphen mit Lichtschranken experimentell erzeugen, etwas komplexere mit dem hervorragenden Sonarmeter, mit dem man überhaupt mit Hilfe von geeigneter Software Einsichten schaffen kann, die mit anderer experimenteller Ausstattung deutlich weniger elegant, für den Lehrer nicht so einfach (geringfügige Justierarbeiten!) und für die Schüler nicht so anschaulich und klar erreichbar sind. |
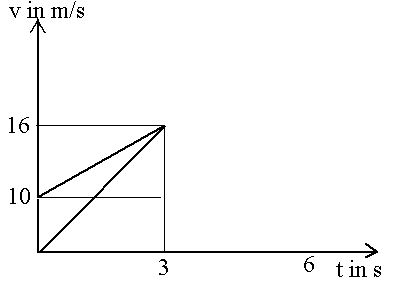
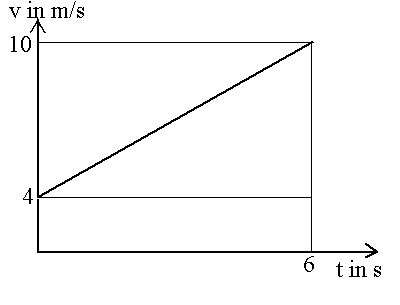 b) Im nächsten Schritt
wird ein t-v-Graph zur Interpretation
vorgegeben mit Anfangsgeschwindigkeit v0 > 0: die
Beschleunigung wird aus dem t-v-Graphen abgelesen (8. Klasse: als
"Geschwindigkeitsänderung pro Zeiteinheit"), die Anfangsgeschwindigkeit
interpretiert.
b) Im nächsten Schritt
wird ein t-v-Graph zur Interpretation
vorgegeben mit Anfangsgeschwindigkeit v0 > 0: die
Beschleunigung wird aus dem t-v-Graphen abgelesen (8. Klasse: als
"Geschwindigkeitsänderung pro Zeiteinheit"), die Anfangsgeschwindigkeit
interpretiert.
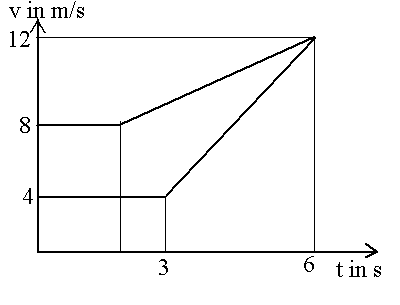 3. Komplexere
t-v-Graphen (ich würde ganz bewusst anfangs noch keine t-x-Graphen
ins Spiel bringen; dann sind Fragen nach dem Begegnungszeitpunkt
ausgeschlossen!): vorgegebene Graphen sollen interpretiert werden, evtl.
indem eine passende Story erfunden wird
wie im nebenstehenden Beispiel. Geschwindigkeiten und Beschleunigungen
sollen quantitativ dem Graphen entnommen werden. Wieder besteht das Ziel
darin, dass die Schüler einerseits den Graphen quantitativ lesen,
andererseits auch, dass sie ihn in eine möglichst realistische Bewegung
kreativ übersetzen, auch den Mut gewinnen, eine quantitative Situation
auch mit ihrer Fantasie zu bewältigen.
3. Komplexere
t-v-Graphen (ich würde ganz bewusst anfangs noch keine t-x-Graphen
ins Spiel bringen; dann sind Fragen nach dem Begegnungszeitpunkt
ausgeschlossen!): vorgegebene Graphen sollen interpretiert werden, evtl.
indem eine passende Story erfunden wird
wie im nebenstehenden Beispiel. Geschwindigkeiten und Beschleunigungen
sollen quantitativ dem Graphen entnommen werden. Wieder besteht das Ziel
darin, dass die Schüler einerseits den Graphen quantitativ lesen,
andererseits auch, dass sie ihn in eine möglichst realistische Bewegung
kreativ übersetzen, auch den Mut gewinnen, eine quantitative Situation
auch mit ihrer Fantasie zu bewältigen.