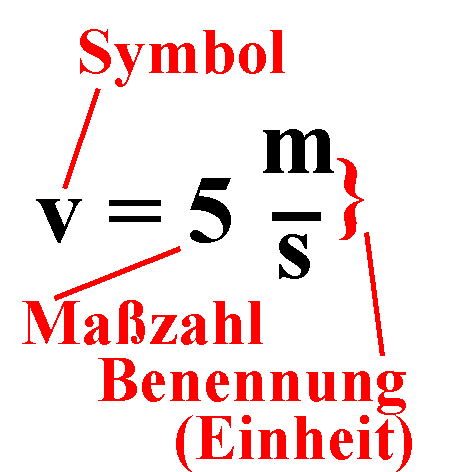Startseite FORPHYS

SG002 Geschwindigkeit im Unterschied zu Tempo © H. Hübel Würzburg 2013

v-Messung Beschleunigung Koordinaten

Glossar Physik für Schülerinnen und Schüler

Impres-sum

Du hast es wahrscheinlich in der Grundschule so gelernt:

Geschwindigkeit soll sein: zurückgelegter Weg dividiert durch die dafür benötigte Zeit.

Leider stimmt das nicht, aus verschiedenen Gründen:

1. So kann man keine Geschwindigkeit definieren, sondern nur das, was der Tachometer im Moped oder Auto anzeigt. Es wird "Tempo" genannt. Auch in anderen Sprachen gibt es einen besonderen Namen dafür, z.B. "speed" im Englischen. Geschwindigkeit heißt dort "velocity".

2. Auch für den Begriff Tempo funktioniert das so nur bei einer gleichförmigen Bewegung, also bei einer Bewegung mit konstantem Tempo.

Was ist im Unterschied dazu "Geschwindigkeit"? Wie kann man sie allgemein definieren?

Geschwindigkeit (engl. velocity) umfasst einerseits "Tempo" (speed), andererseits auch eine Richtungsangabe, nämlich die Richtung, in die sich ein Körper bewegt. Eine Größe, die durch Richtung und Betrag gekennzeichnet ist, ist ein Vektor. Geschwindigkeit als Vektor heißt übrigens im Englischen "velocity"; daher das Symbol v für die Geschwindigkeit.

Tempo (engl. speed) ist der Betrag des Geschwindigkeitsvektors v (velocity), also |v|. Tempo kann nie negativ sein. Ganz gleich in welche Richtung sich ein PKW bewegt, vom Tacho lassen sich nur positive Werte oder 0 ablesen, also das Tempo.

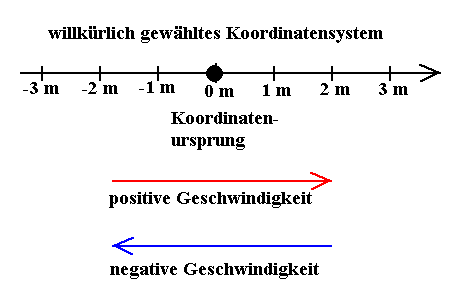
Auch bei einer linearen Bewegung, längs einer Fahrbahn z.B., müssen zwei Richtungen unterschieden werden. Deswegen sollte vor ihrer Untersuchung ein Koordinatenursprung und eine positive Richtung vereinbart werden. Die positive Richtung heißt dann häufig die x-Richtung. Befindet sich der Körper in einer Position in positiver Richtung, ist die x-Koordinate positiv. Befindet er sich auf der anderen Seite des Ursprungs, ist die x-Koordinate negativ.

Ganz ähnlich ist es mit der Geschwindigkeitskoordinate (auch velocity genannt), die dann v_x oder kurz v heißt: Bei einer Bewegung in positive x-Richtung ist die Geschwindigkeitskoordinate v positiv, bei einer Bewegung in negative x-Richtung ist die Geschwindigkeitskoordinate v negativ.  Bei einer linearen Bewegung kann man also die Richtung des Geschwindigkeitsvektors mit dem Vorzeichen der Geschwindigkeitskoordinate v kennzeichnen.

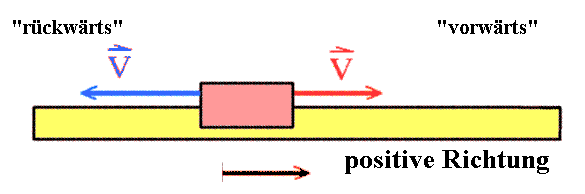Für einen Gleiter auf der horizontalen Luftkissenfahrbahn wird hier veranschaulicht: Bei einer eindimensionalen (linearen) Bewegung und nach Wahl eines Koordinatensystems mit einer positiven Richtung gilt: Je nach Bewegungsrichtung (Richtung des Geschwindigkeitsvektors v) hat die Geschwindigkeitskoordinate v positives oder negatives Vorzeichen.

Noch einmal: Positive und negative Geschwindigkeit(-skoordinate) bei einer linearen Bewegung

Du könntest dich an einer Fahrbahn leicht davon überzeugen, wenn ein Geschwindigkeitsmesser (z.B. ein Sonarmeter) zur Verfügung stünde. Bewegt sich das Fahrzeug in positive Richtung, ist auch die Geschwindigkeitsanzeige positiv, bewegt es sich in negative Richtung, ist die Geschwindigkeit negativ. Wenn das Fahrzeug ruht, ist sie natürlich 0. Am Vorzeichen der Geschwindigkeit kannst du die Bewegungsrichtung erkennen.

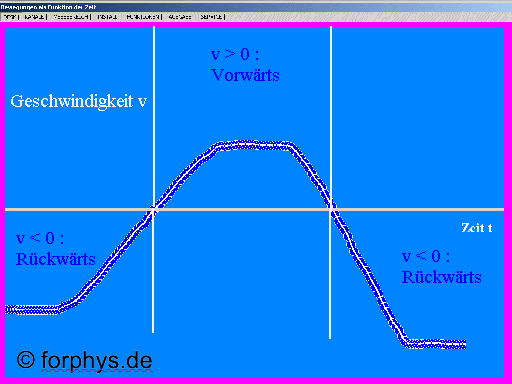Abb. 1: Das ist der t-v-Graph der Bewegung einer Person, aufgenommen mit dem Sonarmeter. Das Vorzeichen der Geschwindigkeitskoordinate verrät die Bewegungsrichtung. Wenn die Geschwindigkeit v = 0 ist, ruht die Person.  Warum verläuft der t-v-Graph zu manchen Zeiten horizontal?

Wie kann nun eine Geschwindigkeit (Vektor!) definiert werden?

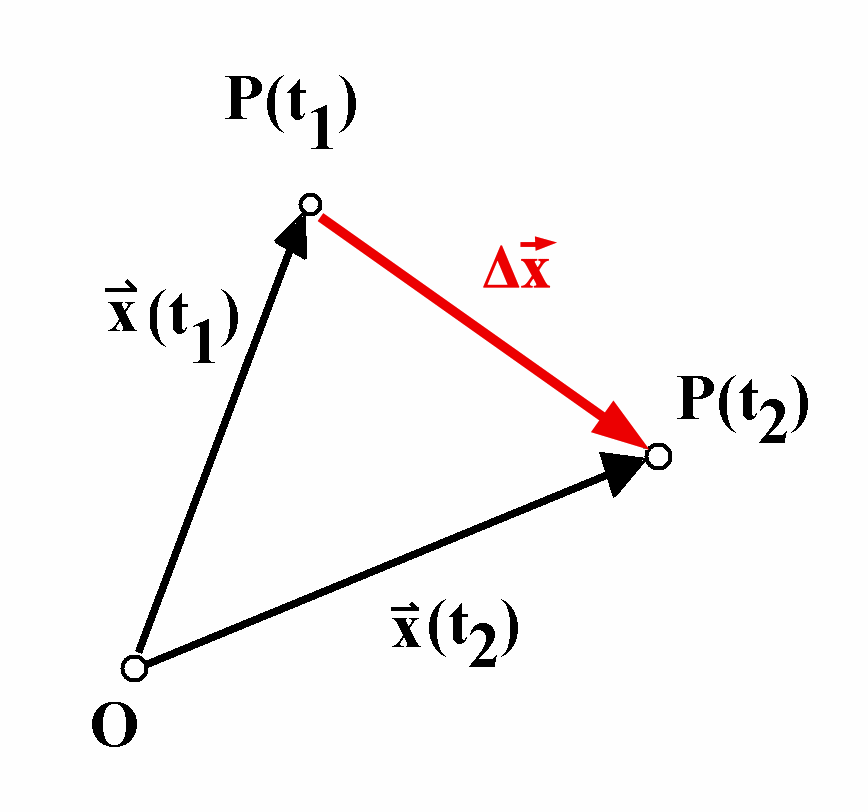Betrachte zwei Zeitpunkte: t1 und t2. Von t1 nach t2 vergeht die Zeitdauer Δt = t2 - t1. Zum Zeitpunkt t1 befinde sich der Körper beim Ort x(t1), zum Zeitpunkt t2 befinde er sich am Ort x(t2). Der Ort hat sich also von  t1 bis t2 verändert um eine "Verschiebung" Δx = x(t2) - x(t1). Δx heißt auch "Ortsänderung" *).

Dann wird die Geschwindigkeit v definiert als

Die Geschwindigkeit v gibt also an, wie sich der Ort x in der Zeiteinheit verändert.

Wenn sich die Geschwindigkeit in dem Zeitintervall Δt ändert, wird dadurch aber nur eine Durchschnittsgeschwindigkeit v_D beschrieben. Die Momentangeschwindigkeit (kurz: Geschwindigkeit) erhält man, wenn man das Zeitintervall Δt so klein wählt, dass sich in ihm die Geschwindigkeit quasi nicht ändert.

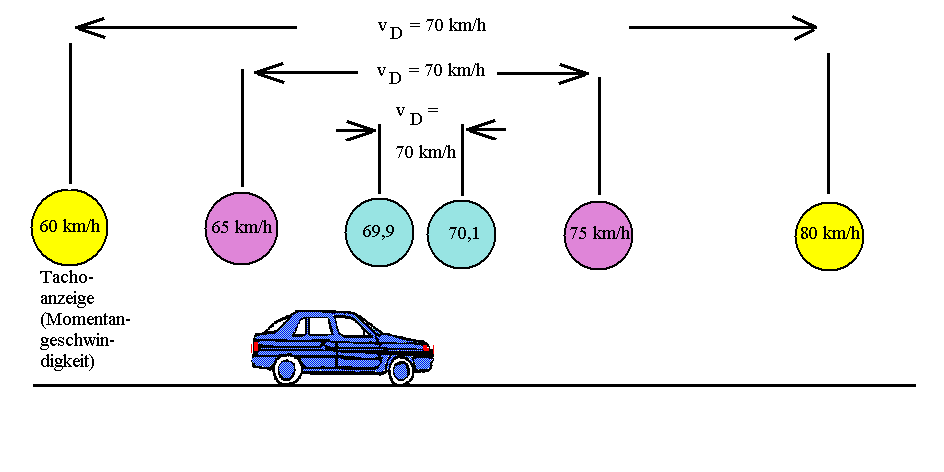Je kürzer das Zeitintervall Δt, desto besser stimmt die Durchschnittsgeschwindigkeit  vD mit der Momentangeschwindigkeit v überein. (Der Tacho zeigt natürlich das Tempo an, das nur bei positiver Geschwindigkeit mit der Geschwindigkeit übereinstimmt.)

Du erkennst den Unterschied zur Grundschul-Definition:

1. ist jetzt die Bewegungsrichtung enthalten, und
2. ist die Nebenbedingung enthalten: "wenn Δt so klein gewählt wird, dass sich in Δt die Geschwindigkeit v quasi nicht ändert".

Bei einer linearen Bewegung kann man die Vektoreigenschaft wieder durch eine einzige  Koordinate beschreiben. Bewegt sich der Körper in positive Richtung von x₁ nach x₂ (jeweils Koordinaten), ist die Verschiebung Δx = x₂ - x₁ positiv, dementsprechend auch der Quotient Δx/Δt, und damit auch die Geschwindigkeitskoordinate v = Δx/Δt. Bewegt sich der Körper in negative Richtung von x₁ nach x₂, ist die Verschiebung Δx = x₂ - x₁ negativ, dementsprechend auch der Quotient Δx/Δt, und damit auch die Geschwindigkeitskoordinate v = Δx/Δt. Daran siehst du auch, dass man die Verschiebung  nicht "Strecke" nennen sollte. Eine Strecke bzw. Streckenlänge kann nie negativ sein! Mit einer Aufgabe erklärst du dir den Unterschied zwischen Ort x und Weg s/Strecke s.

Bei einer linearen Bewegung (eindimensionale Bewegung) gibt es noch eine  weitere Vereinfachung: In der folgenden Abbildung wird dazu ein t-x-Diagramm einer Bewegung dargestellt.

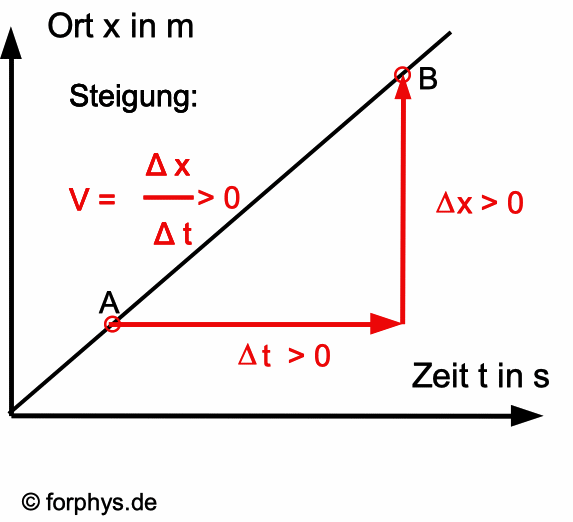Der Quotient Δx/Δt ist dann gerade die Steigung des t-x-Diagramms. Diese Deutung der Geschwindigkeit v (Geschwindigkeitskoordinate) als Steigung des t-x-Diagramms ist für viele Überlegungen äußerst praktisch. Du brauchst nur feststellen, ob der t-x-Graph steigt oder fällt; schon kennst du das Vorzeichen der Geschwindigkeit (positiv oder negativ) und die Bewegungsrichtung. Wie sieht das konkret bei negativer Geschwindigkeit aus?

	Gehe immer von folgendem Durchlaufssinn aus:   Die Hand zeigt nach rechts in Richtung der Fingerspitzen: große positive Steigung - schnelle Bewegung vorwärts
	kleine positive Steigung - langsamere Bewegung vorwärts
	Steigung 0 - der Körper ruht
	negative Steigung - Bewegung rückwärts

.	Wesen	Vorzeichen	Information über
Geschwindigkeit(svektor) v	Vektor	(sinnlos)	Betrag und Richtung
Geschwindigkeit(skoordinate) v (bei linearen Bewegungen)	Koordinate des Geschwindigkeitsvektors v	positiv, negativ und 0	Betrag und Richtung bei linearen Bewegungen, durch das Vorzeichen ausgedrückt
Tempo	Betrag des Geschwindigkeitsvektors v	nie negativ	nur über die "Schnelligkeit"; keine Richtungsinformation

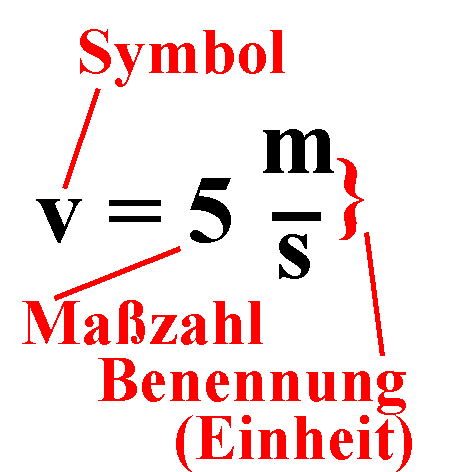
Die Einheit von Geschwindigkeit (velocity) wie von Tempo (speed) ist  1 m/s  bzw. 1 km/h . Die Umrechnung erfolgt so: 1 km/h = 1000 m/h = 1000/3600 m/s = 1/3,6 m/s und damit   1 m/s = 3,6 km/h

Wie man von der Geschwindigkeit zur Ortsänderung Δx kommt, kannst du hier (Flächenverfahren) bzw. hier (Delta-Methode) nachlesen.

Ergänzung: negative Geschwindigkeit

Negative Geschwindigkeit kennzeichnet in einem Koordinatensystem immer eine Rückwärtsbewegung ("rückwärts" im Vergleich zur positiven Koordinatenrichtung).

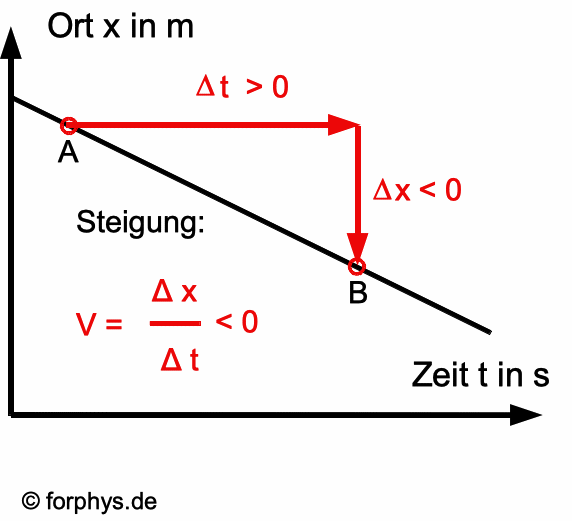Wähle 2 beliebige Punkte A und B auf dem Graphen. Z.B. erfolgt die Bewegung im Laufe der Zeit von A nach B. Verbinde nun A und B durch eine Kette von Pfeilen in Richtung der zugehörige Koordinatenachsen oder entgegengesetzt. Der Pfeil wird positiv gezählt, wenn er gleich gerichtet ist mit der Koordinatenachse, andernfalls negativ. Deshalb haben in der Zeichnung Δt und Δx  unterschiedliches Vorzeichen. Ihr Quotient v = Δx/Δt ist negativ, genauso wie die Steigung des t-x-Diagramms. Das gleiche Verfahren führte oben zur positiven Geschwindigkeit und Steigung.

Wie kann man in der schulischen Mechanik bei eindimensionalen Bewegungen die (Momentan-)Geschwindigkeit messen?