Vorbemerkung

Tempo ist der Betrag der Geschwindigkeit. Der Tacho vom Auto kann nur Tempo anzeigen, d.h. nur nicht negative Werte. Die Geschwindigkeit v ist im allgemeinen ein Vektor, der Aussagen über Betrag und Richtung macht.

Bei einer eindimensionalen Bewegung genügt es, eine Geschwindigkeitskoordinate anzugeben, z.B. v_x. Sie wird dann meistens auch v genannt. Während die Geschwindigkeitskoordinate v beide Vorzeichen haben kann, ist ihr Betrag, also das Tempo, nie negativ. Das Vorzeichen der Geschwindigkeit(skoordinate) beschreibt die Bewegungsrichtung, also vorwärts und rückwärts. Deswegen braucht man bei einer Bewegung die Geschwindigkeit, um den erreichten Ort zu berechnen. Möchte man dagegen beschreiben, welche Strecke zurückgelegt wurde, ganz gleich in welche Richtung, genügt das Tempo, also der Betrag der Geschwindigkeit. Um die Gesamtstrecke zu ermitteln, müssen dann die Strecken von allen zusammenhängenden Zeitabschnitten mit einheitlicher Bewegungsrichtung addiert werden.

Nun zur Aufgabe

Einstein geht mit seinem Hund Zweistein spazieren. Zwischen Wohnung und Patentamt, dem Ziel, liegen 600 m. Einstein läuft mit der Geschwindigkeit v_E = 50 m/min, sein Hund Zweistein anfänglich mit der doppelten Geschwindigkeit v_Z = 100 m/min. Sobald der Hund das Patentamt erreicht hat, kehrt er ohne Zeitverlust um und läuft mit gleichem Tempo zu Einstein zurück. Sobald er Einstein erreicht hat, kehrt er wieder ohne Zeitverlust um, usw. ... 

Welchen Weg s hat der Hund insgesamt zurückgelegt? Problem ist dabei ja wohl, dass er immer kürzere Teilstrecken zurücklegen muss.

Löse diese Aufgabe, indem du

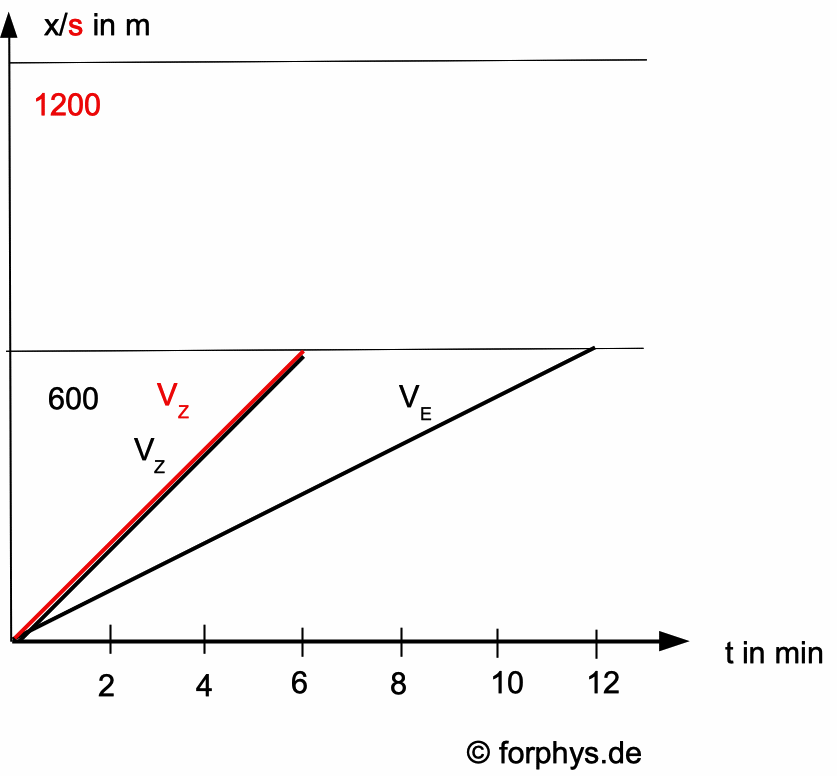
    a) ein Zeit-Ort-Diagramm x(t),

    b) ein Zeit-Weg-Diagramm s(t)

für Einstein und Zweistein zeichnest. Einstein und sein Hund sollen gleichzeitig zur Zeit 0 am Ort x = 0 m bzw. mit dem Weg 0 m starten.

Ergänze die Graphik mit Ort und Weg für den Hund! Alles, was mit "Weg s" zu tun hat, soll rot gezeichnet werden, alles im Zusammenhang mit "Ort x" schwarz.

Du erkennst jetzt den Unterschied zwischen Ort und Weg und die unterschiedlichen Vorgehensweisen. Die Antwort auf die Frage nach dem zurückgelegten Weg des Hunds fällt dir leicht.

Natürlich könntest du auch in den Zeitabschnitten, in denen der Hund zurück läuft, mit seinem Tempo die jeweiligen Teilstrecken ermitteln und alle Teilstrecken addieren. Erleichtert wird das durch die Tatsache, dass der Hund in allen Zeitabschnitten (bis auf die Umkehrpunkte) gleiches Tempo hatte.

In diesem Beispiel ist das Weg-Konzept ausnahmsweise günstiger als das Orts-Konzept, weil nach dem insgesamt zurückgelegten Weg gefragt wurde. Eine Lösung der Aufgabe findest du hier.

Denkst Du mehr mathematisch oder mehr physikalisch? Das Problem von Einstein und seinem Hund soll es enthüllen!

Vor Jahrzehnten las ich eine Anekdote zu diesem Problem: Die Aufgabe wurde verschiedenen Mathematikern und Physikern vorgelegt. Typischerweise sollen Mathematiker zur Lösung dieses Problems mehr Zeit gebraucht haben als Physiker, weil Mathematiker entsprechend Aufgabe b) die einzelnen Teilstrecken aufsummierten, während Physiker in der Regel aus Tempo und Gesamtzeit gleich auf den zurückgelegten Weg s schlossen. Nur der Mathematiker John von Neumann soll noch schneller gewesen sein als die Physiker. Angesprochen, warum er als Mathematiker nicht das gewöhnlich langsamere und kompliziertere Summierungsverfahren angewandt habe, entrüstete sich von Neumann, dass er ja gerade das getan habe. Er konnte einfach deutlich schneller rechnen!

Wenn du lieber die Methode b) gewählt hättest, wäre das - neben vielen anderen - ein Indiz dafür, dass du eher physikalisch denkst.

(Oktober 2023)