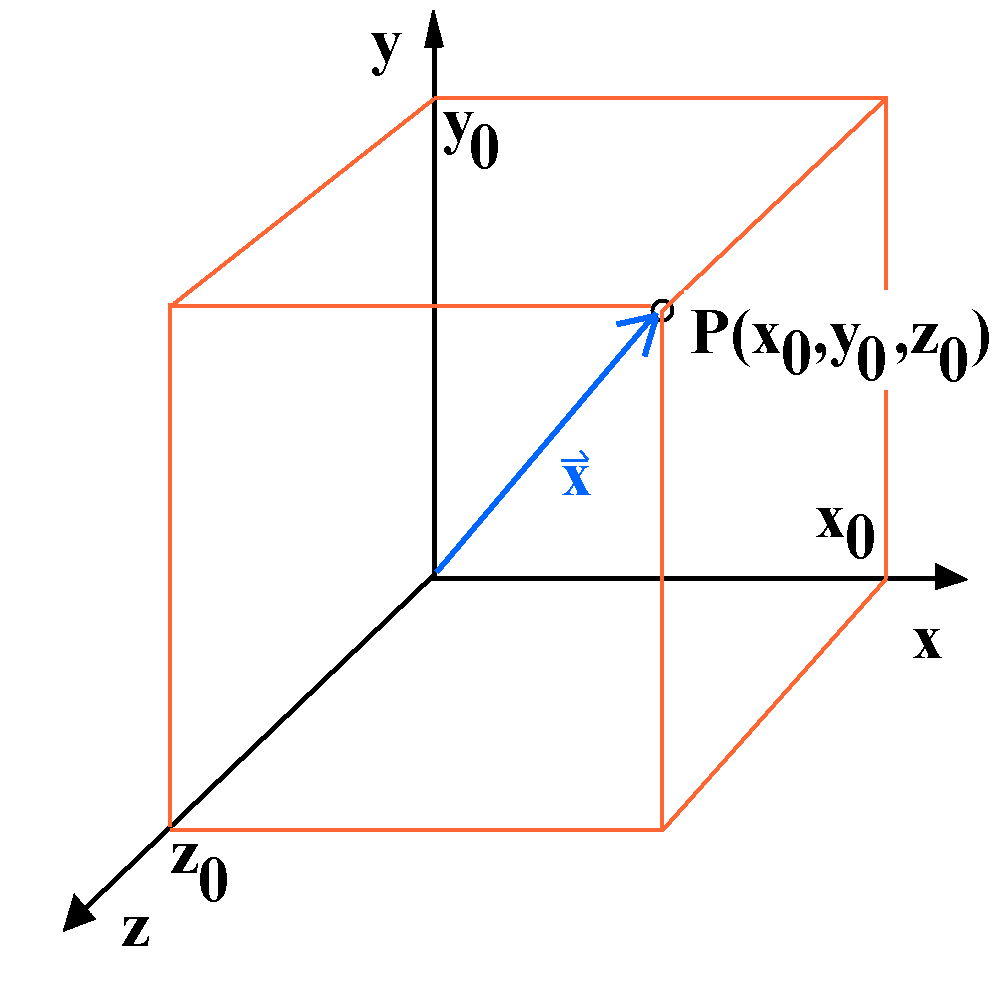Heutzutage beschreibt man Bewegungen mit dem Ort x, der zur Zeit t erreicht ist. Und weil sich der Körper  i.A. in verschiedene Richtungen des Raums bewegen kann, muss man eine Aufeinanderfolge von Orten im dreidimensionalen Raum im Laufe der Zeit betrachten. Der jeweils "erreichte Ort" wird häufig durch die drei Koordinaten x, y, z im Raum beschrieben. Mathematisch fasst man die drei Koordinaten zu einem Vektor x, dem Ortsvektor, zusammen.

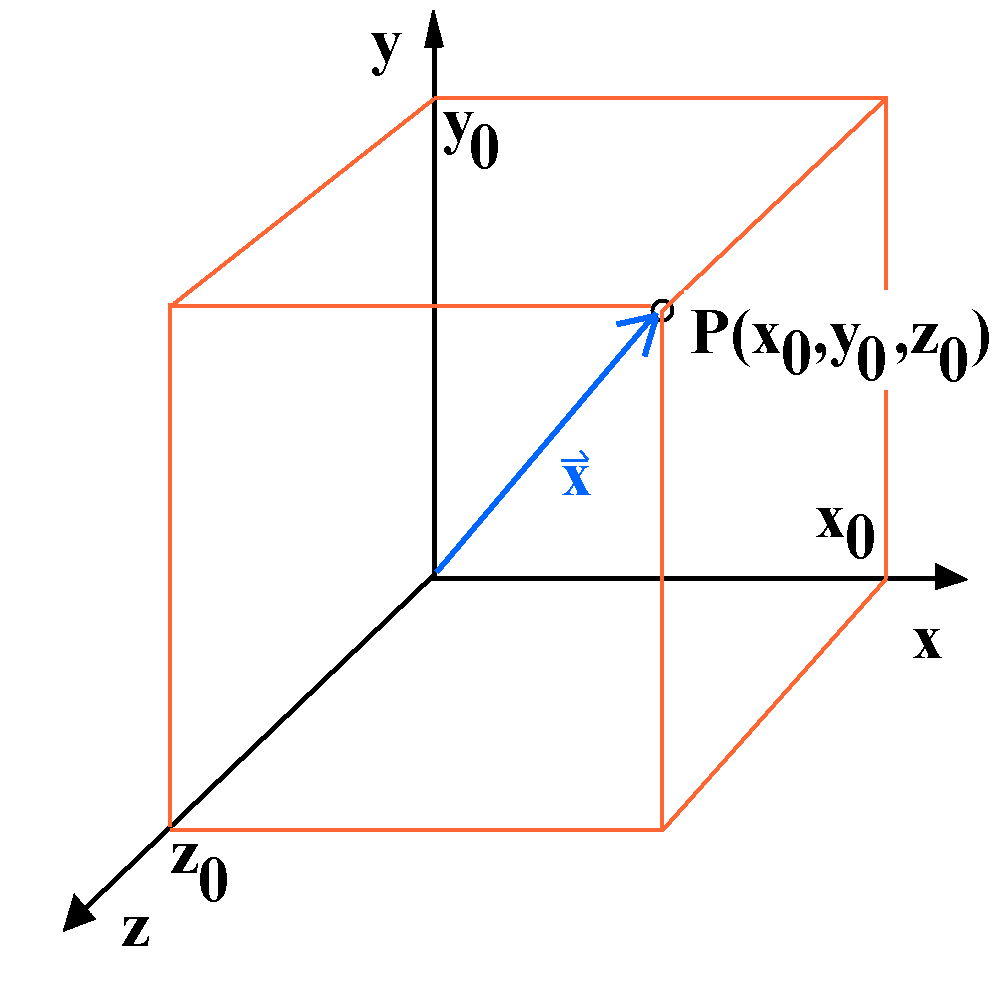Hier wird ein kartesisches Koordinatensystem mit senkrecht aufeinanderstehenden Koordinatenachsen verwendet. Der Ortsvektor x des Punktes P ist blau eingezeichnet. "Startpunkt" des Vektorpfeils ist im Koordinatenursprung, "Zielpunkt" beim jeweils betrachteten Punkt P. In der Zeichnung sind die Koordinaten des betrachteten Punktes mit einer kleinen 0 versehen, damit man sie von den Koordinatenachsen unterscheiden kann. Im Text ist das nicht der Fall. x0, y0 und z0 sind zunächst die Punktkoordinaten von P. Sie sind aber zugleich die Vektorkoordinaten des Vektors x.

Wenn man dann eine Bewegung durch den Ort in Abhängigkeit von der Zeit t beschreiben möchte, gibt man die Vektoren x(t) an.

Natürlich kann man auf die eine Koordinate verzichten, wenn die Bewegung z.B. ausschließlich auf einer Tischplatte erfolgt (Bewegung in einer Ebene). Man kann auf 2 Koordinaten verzichten, wenn die Bewegung längs einer geraden Schiene oder einer Fahrbahn erfolgt (geradlinige Bewegung). Es verbleibt aber mindestens eine Koordinate, die sich im Lauf der Zeit t verändert. Sie wird in der Regel x(t) (ohne Vektorzeichen) genannt.

Während "Wege" eigentlich nur 0 oder positiv sein können, genauso wie Beträge von Vektoren, kann eine Ortskoordinate auch negativ sein. Das setzt voraus, dass vor der Beschreibung oder Untersuchung der Bewegung, auch bereits im eindimensionalen Fall (geradlinige Bewegung), ein Koordinatenursprung und eine positive Koordinatenrichtung vereinbart wurden. Das kann ganz willkürlich geschehen, aber häufig vereinfacht eine bestimmte Wahl die Überlegungen sehr stark.

In der Mathematik würde man von der Wahl einer geeigneten "Basis" sprechen.

Ist das geschehen, bedeutet eine positive Ortskoordinate, dass sich der Körper in positive Koordinatenrichtung vom Ursprung entfernt hat, eine negative Ortskoordinate, dass der Körper entgegengesetzt dazu vom Ursprung entfernt ist.

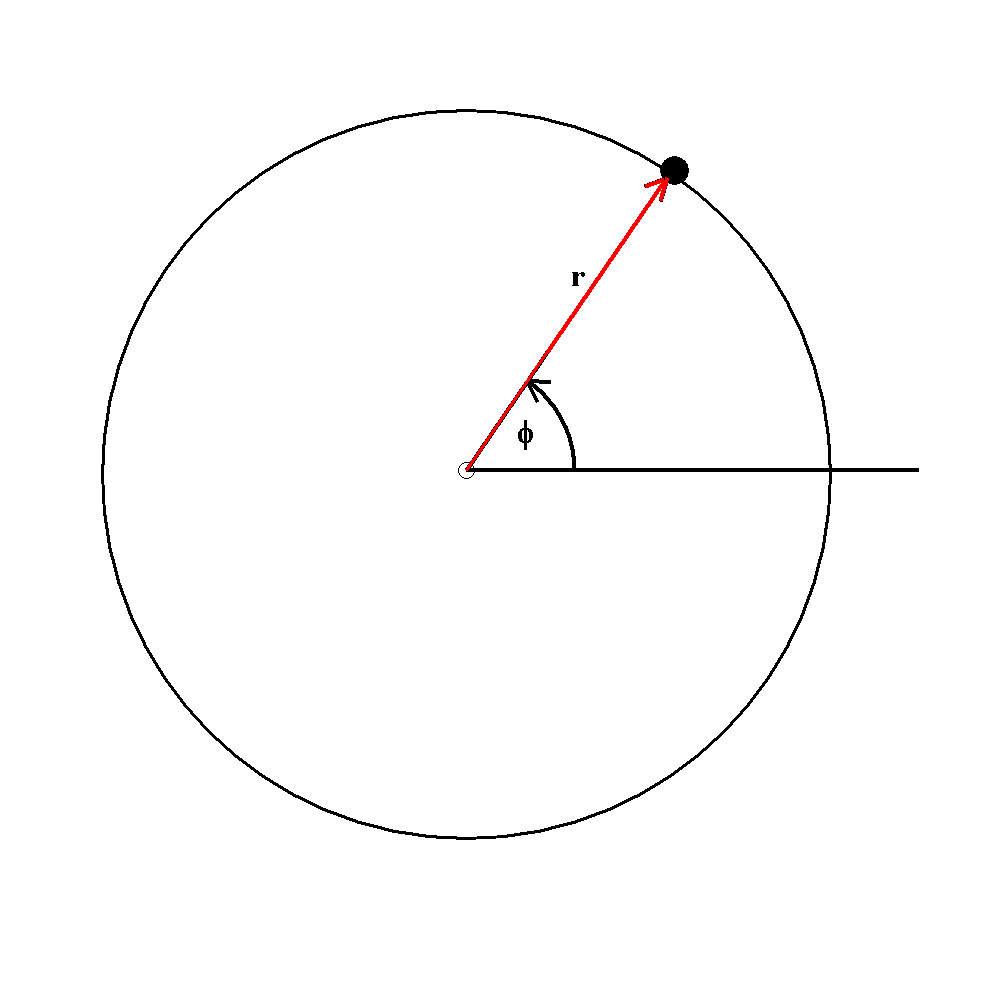Außer einem kartesischen Koordinatensysem mit den Koordinaten x, y und z gibt es noch andere. Bei einer Kreisbewegung kommt es offenbar nur auf eine Koordinate an, die Winkelkoordinate φ . Bei einer Ellipsenbahn, wenn der Radius r nicht mehr konstant ist, sind r und φ besonders geeignet. Das ist z.B. bei der Planetenbewegung von Interesse. Prinzipiell ist es gleichgültig, welches Koordinatensystem du verwendest. Manchmal kannst du dir aber das Leben sehr einfach machen, wenn du "dem Problem angepasste Koordinaten" verwendest. Beim Studium der Planetenbewegung haben sich so die oben erwähnten Polarkoordinaten bewährt.

In vielen Fällen braucht man die 3 Koordinaten gar nicht zu kennen, sondern kann - viel einfacher - mit dem Ortsvektor x in "koordinatenfreier Schreibweise" allein schon argumentieren.

Kann man Vektoren koordinatenfrei beschreiben, kommt es auf die Wahl des Koordinatensystems überhaupt nicht an.

.

( September 2013 )