 |
|
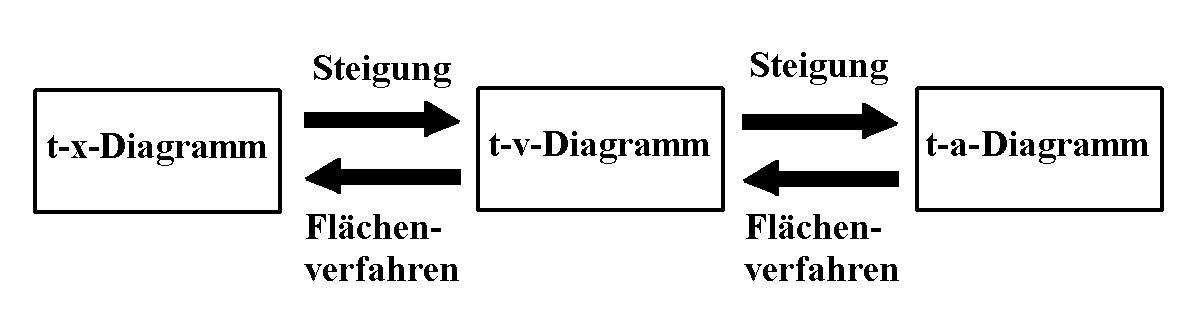
Abb. 1: Von
a zu x mit dem Flächenverfahren, von x
zu a mit der Steigung
|
|
SG141 Das Flächenverfahren der Mechanik ©
H. Hübel Würzburg 2013
|
Impres-sum |
Das Flächenverfahren ist eine anschauliche Methode, um in
der Bewegungslehre bei einfachen Zeitabhängigkeiten das mathematische
Verfahren der "Integration" durchzuführen.
So kommt man bei der in der Schule meist konstanten
Beschleunigung vom t-a-Diagramm für einen Zeitabschnitt Δt von
der Anfangsgeschwindigkeit v0 zu Beginn des Zeitintervalls
zur Geschwindigkeit v am Ende des Zeitintervalls mittels v = v0
+ Δv, wobei die Geschwindigkeitsänderung Δv gerade der Rechtecksfläche
unter dem t-a-Diagramm im Zeitabschnitt Δt entspricht.
Ganz entsprechend kommt man im t-v-Diagramm vom Anfangsort x0 zu Beginn des Zeitintervalls Δt zum Ort x am Ende des Zeitabschnitts durch x = x0 + Δx, wobei die Ortsänderung Δx gerade der Dreiecks- oder Trapezfläche zwischen dem t-v-Graphen und der Zeitachse im Zeitabschnitt Δt entspricht*). Das lässt sich für solch einfache Fälle leicht plausibel machen oder beweisen; für allgemeinere Fälle, wenn a oder v nicht konstant sind, lässt es sich plausibel machen, indem die Zeitabschnitte Δt so klein gewählt, dass in ihnen a bzw. v zumindest in guter Näherung konstant sind.
 |
|
Abb. 1: Von
a zu x mit dem Flächenverfahren, von x
zu a mit der Steigung
|
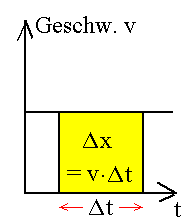 |
Abb. 2: Das Verfahren ist leicht anwendbar und leicht zu merken, berücksichtigt immer korrekt die jeweiligen Anfangsbedingungen v0 und x0, kann auch in komplexeren Fällen (z.B: Überholvorgängen mit Anfangsbedingungen) geometrisch ohne Formelkenntnis angewendet werden, und ermöglicht es, von dem leichter zu durchschauenden t-v-Diagramm zum komplexeren t-x-Diagramm zu kommen. |
*) Hier wird etwas gemogelt:
Eine Fläche ist immer positiv, dagegen können Ortsänderung Δx und
Geschwindigkeitsänderung Δv beide Vorzeichen haben. Wenn man sich aber
beim Ansatz der "Fläche" gar nicht um die Vorzeichen kümmert, sondern
formal mit den "Seiten" des Rechtecks, Δv und Δt z.B., rechnet, ganz
gleich welches Vorzeichen diese haben, kommt man zum vorzeichenrichtigen
Ergebnis. Beispiel: negatives Δv < 0, positives Δt. Die Fläche im
mathematischen Sinn wäre /Δv/·Δt = - Δv·Δt. Das kann nicht verwendet
werden. Dagegen ist Δx = Δv·Δt genauso wie die Ortsänderung Δx in diesem
Fall negativ. Du kannst den Begriff "Flächenverfahren" auch
als eine Merkregel auffassen. Du erhältst das richtige Ergebnis für die
Ortsänderung Δx, wenn du Δv und Δt mit ihrem jeweiligen
Vorzeichen miteinander multiplizierst.
In der Abb. 2 sind Δv und Δt positiv. Die Fläche
bestimmt eigentlich den Weg s im Zeitintervall Δt. Dieser stimmt hier
aber mit der Ortsänderung Δx überein: Δx = Δv·Δt. Die Problematik
entspricht dem Unterschied zwischen Fläche unter einem
Funktionsgraphen und dem Integral.
Wenn man hier eine Betragsbildung vorschlägt, wird man
i.A. keine Ortsänderung Δx erhalten, sondern allenfalls eine
Wegänderung Δs.
Das Flächenverfahren wurde erstmals von Nikolaus Oresme (vor 1330 - 1382) zum Beweis der Merton-Regel (1335) angewandt, die die Grundlage der Zeitmitten-Methode ist.
( September 2013 )