A Was ist eine Ellipse?

Zur Geometrie der Ellipse

Messung der geringen Exzentrizität der Erdbahn

B Worin besteht die Aussage des Gesetzes?

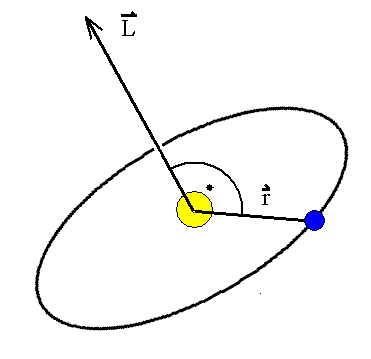
1. Die Bahnkurve der Planeten ist eine in sich geschlossene Ellipse. Nach jedem vollen Umlauf befindet sich ein Planet wieder an derselben Stelle. 2. Die Bahnkurve verläuft in einer Ebene. Die Lage dieser Ebene kann durch einen "Flächenvektor" gekennzeichnet werden, der auf dieser Ebene senkrecht steht (im Bild längs L). Es gibt offenbar keine Kraftkomponente und keine Geschwindigkeitskomponente, die den Planeten aus dieser Ebene herausführt. 3. Die Sonne steht nicht im Zentrum der Ellipse, sondern in einem ihrer Brennpunkte. (Auch ein Kraftgesetz nach Hooke könnte als eine der möglichen Bahnkurven eine Ellipse liefern, aber mit dem Kraftzentrum im Zentrum der Ellipse.)

C Welche physikalischen Folgerungen ergeben sich aus dem 1. Kepler-Gesetz:

1. Nur ein bestimmtes Kraftgesetz (nämlich mit der bekannten Gravitationskraft proportional 1/r²) kann eine solche Bahnform hervorrufen. Man kann an Beispielen zeigen, das bereits geringfügige Abweichungen vom Gravitationsgesetz zu nicht geschlossenen Bahnen führen (Simulation mit dem PC-Programm KEPLER)

2. Die wirkende  Kraft (entsprechend dem Gravitationsgesetz) kann kein Drehmoment hervorrufen, das die Bahnebene verändert. Das legt eine Zentralkraft nahe, die dann schließlich durch das 2. Kepler-Gesetz bewiesen wird. (vgl. Abbildung)