|
|
||
| Die beiden Punkte F1 und F2 heißen Brennpunkte. | Man kann einen Kreis als eine Ellipse mit zusammenfallenden Brennpunkten auffassen. Kreis und verschiedene Ellipsen unterscheiden sich durch die Exzentrizität. |
© Horst Hübel Würzburg
2005 - 2014
Die Ellipse |
Am einfachsten versteht man eine Ellipse mit der so genannten "Gärtnerkonstruktion". Die heißt so, weil früher Gärtner elliptische Beete in dieser Weise angelegt haben. Sie haben zwei Pflöcke an zwei nicht zusammenfallenden Punkten F1 und F2 in den Boden geschlagen, eine Schnur sehr locker zwischen sie gebunden, und sind dann mit einem weiteren Pflock P so um die beiden festen Pflöcke herumgefahren, dass die Schnur zu beiden Seiten immer gespannt blieb. P beschrieb dann eine Linie, eben die Ellipse.
Mathematisch ist klar, dass die Summe der beiden Strecken PF1 und PF2 konstant ist. Genau das ist die Definition der Ellipse:
| Eine Ellipse ist der geometrische Ort aller Punkte P, die von 2 verschiedenen Punkten F1 und F2 zusammen konstanten Abstand haben (c + d = konst ). |
|
|
||
| Die beiden Punkte F1 und F2 heißen Brennpunkte. | Man kann einen Kreis als eine Ellipse mit zusammenfallenden Brennpunkten auffassen. Kreis und verschiedene Ellipsen unterscheiden sich durch die Exzentrizität. |
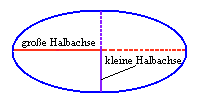 |
Eine Ellipse ist gekennzeichnet durch ihre große und kleine
Halbachse (a und b).
Die Exzentrizität ist bestimmt durch das Verhältnis b/a der beiden Halbachsen. |
| Maßgrößen für die Exzentrizität sind:
1. der Bahnparameter k = a2/b (manchmal auch p genannt) 2. die numerische Exzentrizität ε2 = 1 - k/a = 1 - (b/a)2 3. die lineare Exzentrizität: e2 = a2 - b2 Die lineare Exzentrizität e ist der Abstand eines Brennpunkts vom Zentrum der Ellipse.
Der Brennpunktsabstand ist 2·a·ε = 2·e |
Es gibt verschiedene Darstellungen für die
Ellipse:
Polarform in Polarkoordinaten mit dem Radius r und dem Winkel φ ( ε numerische Exzentrizität):
|
k
r = -------------------------- 1 + ε cos ( φ ) |
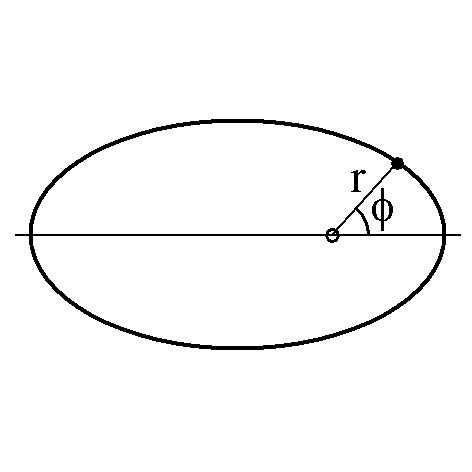 |
Wenn φ = 0o gilt r = k/(1 + ε), wenn φ = 360o gilt r = k/(1 - ε), wenn φ = 90o gilt r = k .
Darstellung in kartesischen Koordinaten mit den Halbachsen a und b:
| (x/a)2 + (y/b)2 = 1 | 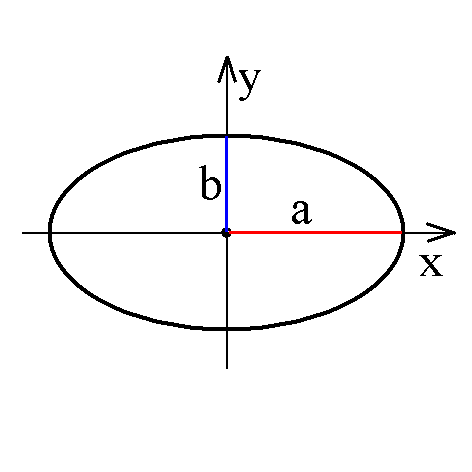 |
x = 0 liefert y = +/- b; y = 0 liefert x = +/- a.