Als Lehrer haben wir uns angewöhnt, im Zusammenhang mit Stromstärke und Spannung kausal zu denken: Ich gebe eine bestimmte Spannung (z.B. auch mit ihrem Zeitverlauf) vor und beobachte, welche Stromstärke sie zur Folge hat. Hier soll eine Möglichkeit vorgestellt werden, mit der eine bestimmte Stromstärke vorgegeben wird und die resultierende Spannung oder eine andere Messgröße untersucht wird. Dieses Verfahren erleichert das Verständnis einiger physikalischer Erscheinungen im Unterricht im Zusammenhang mit Spule und Kondensator.

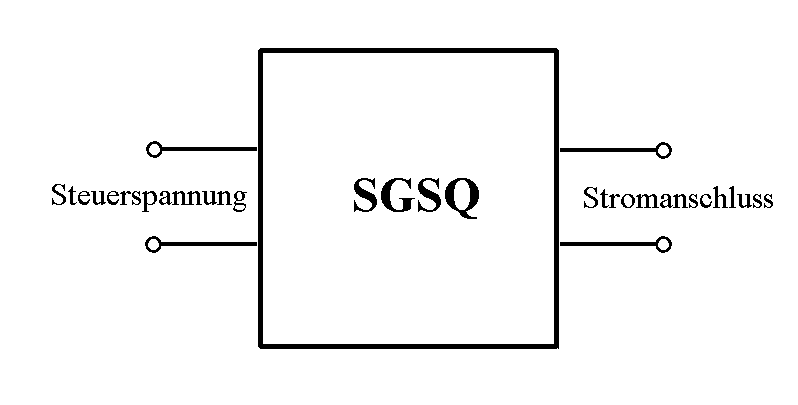Abb. 1: Prinzip einer spannungsgesteuerten Stromquelle: Nach Anschluss eines stromleitenden Bauelements wird ein zur Steuerspannung proportionaler Strom erzeugt, ganz gleich (in weiten Grenzen), welchen Widerstand das Bauelement hat. Ich nenne die Schaltung manchmal auch "Strompumpe": Ein hineinfließender Strom wird auch durch den Stromanschluss gepumpt. Für den Physik-Unterricht heißt das, dass man einen bestimmten Zeitverlauf der Stromstärke vorgeben kann, der besonders deutlich physikalische Zusammenhänge demonstriert.

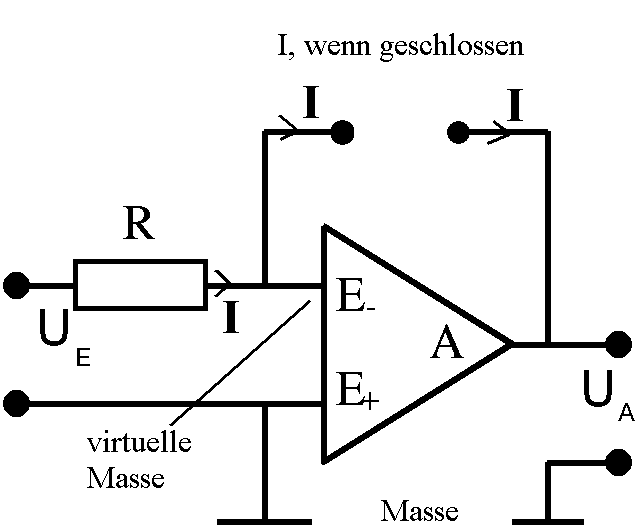Abb. 2: Grundschaltung einer spannungsgesteuerten Stromquelle mit Hilfe eines Operationsverstärkers. Wenn man die Schaltung so auffasst, kommt es auf die Ausgangsspannung UA weniger an. Als Ausgang dienen dann die beiden "Stromanschlüsse". In erster Näherung ist das Grundprinzip sehr einfach zu verstehen. Man braucht nur zwei typische Kennzeichen eines Operationsverstärkers: (1) Prinzip der virtuellen Masse: Das Potenzial beider Eingänge kann sich bei funktionierender Gegenkopplung (zwischen Ausgang A und Eingang E-) höchstens um mV unterscheiden; in erster Näherung ist diese Potenzialdifferenz also Null, und da ein Eingang sicher auf Massepotenzial liegt, liegen beide in guter Näherung auf Massepotenzial. Für die Schaltung bedeutet das, dass die Stromstärke I  (bei Betriebsbedingungen) allein durch UE und R bestimmt ist: I = UE/R. (2) Quasi unendlicher Eingangswiderstand: Es kann kein Strom in den OV hineinfließen. Wenn ein Strom entsprechend (1) fließt, kann er höchstens über den Gegenkopplungszweig fließen. Dadurch ist Größe und Richtung des Stroms im Gegenkopplungszweig (zwischen den "Stromanschlüssen") festgelegt. An den "Stromanschlüssen" können alle möglichen stromdurchlässigen Bauteile angeschlossen werden. Bei dieser wie allen folgenden Schaltskizzen sind die Anschlüsse für die bipolare Spannungsversorgung (+ UB, - UB) nicht eingezeichnet. Es könnten z.B. 2 Stück 9V-Block-Batterien verwendet werden.

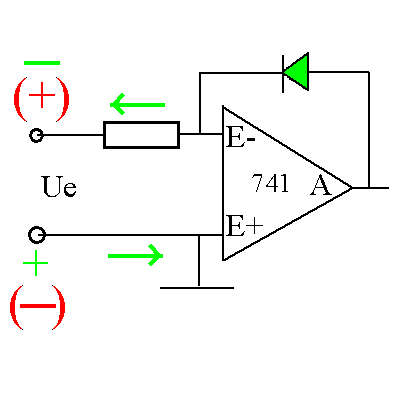Abb. 3: Ein Präzisionsgleichrichter 1. Die Diode wirkt als Ventil; nur bei einer bestimmten Polarität kann ein zur Spannung proportionaler Strom fließen. Die Ausgangsspannung wird nicht genutzt. Der Strom durch den Widerstand (und die Diode) ist unabhängig von einer Schwellenspannung der Diode. Bei richtiger Polarität ist die Stromstärke durch die Diode proportional zur Spannung Ue. 2. Die Schaltung dient auch als eine Art Dimmer für die Leuchtdiode. Wenn Ue und R einen Strom von 1 mA (5 mA, 10 mA, ... ) durchlassen, fließt dieser Strom auch durch die LED. Man kann auf diese Weise einen wohldefinierten Strom durch die LED fließen lassen ohne an Hand der Kennlinie zu untersuchen, welche Spannung zu einem bestimmten Strom gehört. 3. Ein solcher Gleichrichter ist Voraussetzung für einige Versuche, die anderswo erklärt sind: Ermittlung der Gesetzmäßigkeit für die magnetische Energie in einer stromdurchflossenen Spule, Messung der Induktivität, Nachweis des Energieerhaltungssatzes bzgl. elektrischer und magnetischer Energie. 4. Ersetzt man die Diode durch einen Brückengleichrichter, so fließt ein gleichgerichteter Strom, der in jeder Halbwelle proportional zur jeweiligen Wechselspannung ist.

Hinweis: Test der Strompumpe

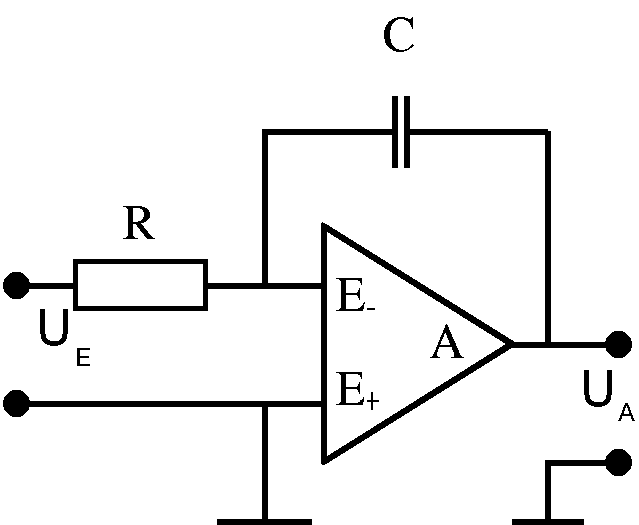Abb. 4: Ladungsmesser An den Stromausgang wird ein Kondensator angeschlossen. Wenn die Eingangsspannung Ue konstant ist, fließt auch ein konstanter Strom I = Ue/R . Er fließt auf den Kondensator und lädt ihn, wie der Lehrer weiß, gemäß ΔQ = C·ΔU, also gemäß I = C·ΔU/Δt auf. Bei konstanter Stromstärke I ändert sich die Kondensatorspannung und damit die Ausgangsspannung UA linear mit der Zeit. Die Schaltung kann benutzt werden als Ladungsmesser: Alle angebotenen Ladungen werden auf den Kondensator gepumpt und können durch UA gemessen werden. Elektronikfachleuten ist die Schaltung als Integrator bekannt.

Schülerversuche mit dem Ladungsmesser

Ohne die Theorie des OV in seiner Schaltung zu verstehen kann der Schüler die Funktion als Ladungsmesser empirisch untersuchen:

a) Es fließe ein konstanter Strom I. Er transportiert in der Zeit t eine Ladungsmenge Q gemäß Q = I·t. Die richtige Funktion erkennt man am linearen Anwachsen der Anzeige mit der Zeit (nicht als Spannung, sondern als Maß für Q aufgefasst; Angabe in Skalenteilen).

(Dimensionierung: R = 10 MOhm, C = 1 µF. Es genügt ein OV vom Typ 741). Bei einer Eingangsspannung U_e = 5 V fließt ein Strom von 0,5 µA. In einer Sekunde wird die Ladungsmenge Q = 0,5 µAs transportiert, die die Spannung um ΔU = ΔQ/C = 0,5 V anwachsen lässt).

b) Es werden getrennte, jeweils gleiche Ladungsportionen ΔQ zugeführt. Dementsprechend steigt die Anzeige in gleichen Schritten an. (Dimensionierung: C = 2 - 10 nF, R = 10 kOhm; die jeweils (ungefähr) gleichen Ladungsportionen wurden durch Abstreifen mittels eines Ladungslöffels von den Haaren erhalten. Man muss einen OV CA3140 oder ähnlichen mit sehr geringer Offset-Spannung und extrem kleinen Offset-Strom verwenden. Mit C = 2 nF kommt man schon in den Grenzbereich.)

Beide Versuche wurden an meinen Schulen mit großem Erfolg als Schülerversuche durchgeführt und dienten dazu, die Sch von der Funktion der Schaltung als Ladungsmesser zu überzeugen. Nur für den Versuch a) konnte der OV-Baustein von Leybold mit dem OV 741 verwendet werden. Für den Versuch b) musste das Gehäuse geöffnet und der OV 741 durch z.B. CA 3140 ersetzt werden. Er passt genau in die Fassung.

Im Folgenden dienten weitere Schülerversuche mit dem jetzt bekannten Ladungsmesser dazu, wegen Q prop. U, eine Kapazität C zu definieren, und herauszufinden, wovon die Kapazität eines Plattenkondensators abhängt. Auch Influenzversuche sind möglich.

Obwohl die Schaltung unempfindlicher ist als handelsübliche Ladungsmesser, hat sie doch einen Vorteil: Alle angebotenen Ladungen werden gemessen, während bei handelsüblichen Geräten und anderen Vorschlägen der Ladungsmessung mit einem OV, die auf einer Elektrometerschaltung beruhen, der ladungstragende Kondensator mit einem Kondensator hinter dem Eingang parallelgeschaltet wird. Dieser nimmt dann nur einen (berechenbaren) Teil der angebotenen Ladungen auf und erzeugt damit eine ladungsproportionale Spannung, die bei solchen Typen von Ladungsmessern gemessen wird. Für quantitative Messungen müsste hier ein Korrekturfaktor berücksichtigt werden.

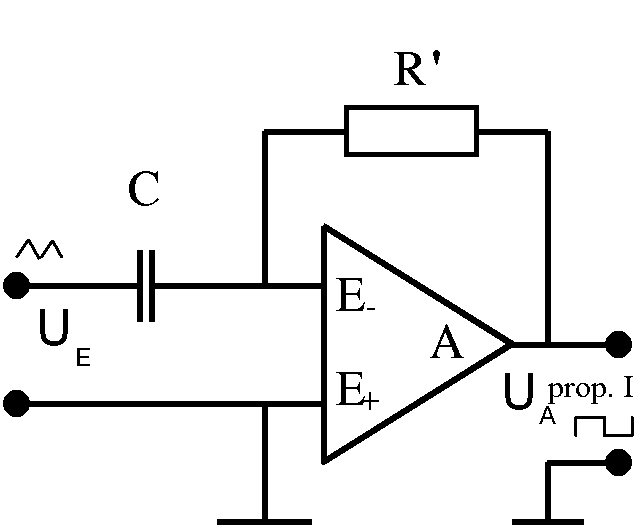Abb. 5: Messung des Ladestroms eines Kondensators durch eine Spannung An den Kondensator wird eine wohldefinierte Ladespannung gelegt. Sie hat einen evtl. sehr kleinen Strom durch C und R' zur Folge, der durch die Ausgangsspannung des OV gemessen wird. Als Lehrer weiß man: Wegen ΔQ/Δt = C · ΔU/Δt = I hat eine linear veränderliche Spannung am Eingang einen abschnittsweise konstanten Strom zur Folge. Der Schüler findet bei einer angelegten Dreiecksspannung dagegen schnell experimentell: ΔU/Δt prop. I. Aus dem Vorzeichen von I bzw. der Richtung des Stroms schließt der Sch auf Laden von C bzw. Entladen. Das erklärt ihm, wie eine sich dreiecksförmig verändernde Wechselspannung einen dauernden Wechselstrom (mit rechtecksförmigen Zeitverlauf) durch C zur Folge haben kann. Der Zusammenhang dU/dt prop. I hilft auch bei einer sinusförmigen Wechselspannung den Stromverlauf qualitativ und die Phasenbeziehung zwischen Strom und Spannung zu erklären: Erst muss ein Strom fließen, bevor sich eine Spannung am Kondensator aufbauen kann; der Strom eilt der Spannung voraus. Die Beziehung fordert eine Erklärung, und siehe da, es handelt sich um die Zeitableitung der längst bekannten Beziehung Q = C·U. Damit ist auch die Proportionalitätskonstante erklärt: I = C·ΔU/Δt . Der Versuch wird eingesetzt zur Vorbereitung der Wechselstromlehre beim Kondensator. Zur Dimensionierung. C = 10 µF und ΔU = 5 V in 10-2 s (50 Hz) führt zu ΔU/Δt = 5·102 V/s und I = 5·102 V/s 1 · C = 5·10-3 A. Mit R' = 1 kOhm wird daraus UA = 5 V. In der Elektronik ist die Schaltung als Differenzierer bekannt.

 

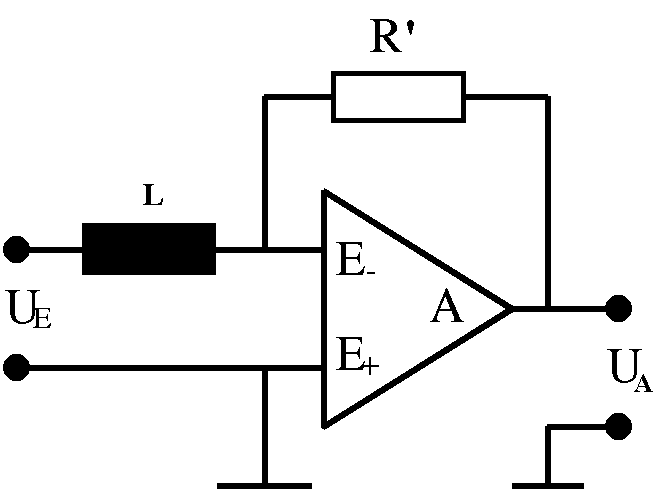Abb. 6: Eine abschnittsweise konstante Spannung an einer idealen Spule würde in dieser Schaltung für einen linear wachsenden oder fallenden Strom durch den Widerstand R sorgen, der durch die Ausgangsspannung gemessen wird. Bei einer realen Spule mit ihrem Innenwiderstand und dem endlichen Ausgangswiderstand des Rechtecksgenerators dürfte es allerdings unmöglich sein, so eine konstante Induktionsspannung zu erzeugen.

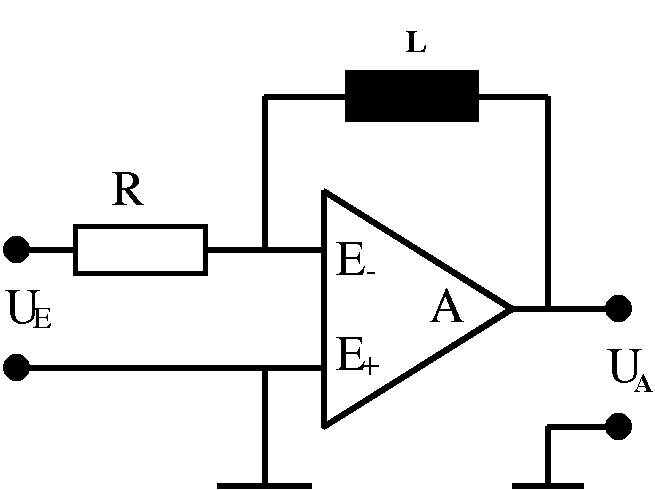Abb. 7: Eine Spule mit vorgegebem Zeitverlauf des Stroms Eine linear wachsende und fallende (dreiecksförmige) Spannung am ohmschen Widerstand R erzeugt einen proportionalen Strom I, der auch durch die Spule mit der Induktivität L fließen muss. Als Lehrer weiß man, dass als Folge gemäß Uind = - L·ΔI/Δt eine abschnittsweise konstante Selbstinduktionsspannung an der Spule entstehen muss, die auch zwischen Ausgang A und Masse liegt, also durch die Ausgangsspannung UA gemessen wird. Bei einer realen Spule mit ihrem zu L in Reihe geschalteten Innenwiderstand Ri entsteht zusätzlich noch ein Spannungsabfall. Dann ist die Ausgangsspannung UA = - L·ΔI/Δt - I·Ri . Erfreulicherweise gibt es Spulen mit relativ großer Induktivität (L = 0,1 H, ... ) und kleinem Innenwiderstand (Ri = 1,5 Ohm). In brauchbarer bis guter Näherung kann dann der Spannungsabfall vernachlässigt werden. Dem Leser ist längst klar, weshalb eine Dreiecksspannung gewählt wurde. An der abschnittsweise konstanten Selbstinduktionsspannung erkennen die Sch besonders einfach den Zusammenhang zwischen der Selbstinduktionsspannung und der Steigung (Ableitung) des t-I-Graphen, sogar dann, wenn sie mit dem Ableitungsbegriff noch nicht vertraut sind.

Der Versuch kann als Schülerversuch oder als Demonstrationsversuch durchgeführt werden.

Beim Demonstrationsversuch wird als Steuer-Spannungsquelle ein handelsüblicher Funktionsgenerator verwendet mit Frequenzen zwischen typisch 10 und 400 Hz. Die Selbstinduktionsspannung wird mit einem Oszilloskop gemessen. Bei einem Zweikanaloszilloskop kann man dann Stromstärke (proportional zum Eingangssignal) und Selbstinduktionsspannung vergleichen. Als Operationsverstärker-Baustein kann die originale Variante von Leybold mit einem OV 741 verwendet werden oder ein leicht zusammenzubastelnder Eigenbau-OV mit demselben OV bzw. mit einem TI 081. Ich schlage einen Eingangswiderstand R mit 2 kOhm vor. Abb. 8  zeigt den einfachen Aufbau auf einem Leybold-Schaltbrett mit dem Spulenbaustein. Die Eingangsspannung wird am Funktionsgenerator eingestellt. Da/wenn die Sch noch nichts von Selbstinduktion wissen, wird die Selbstinduktionsspannung zunächst nur "Spannung an der Spule" oder "Spannung U_L" genannt.

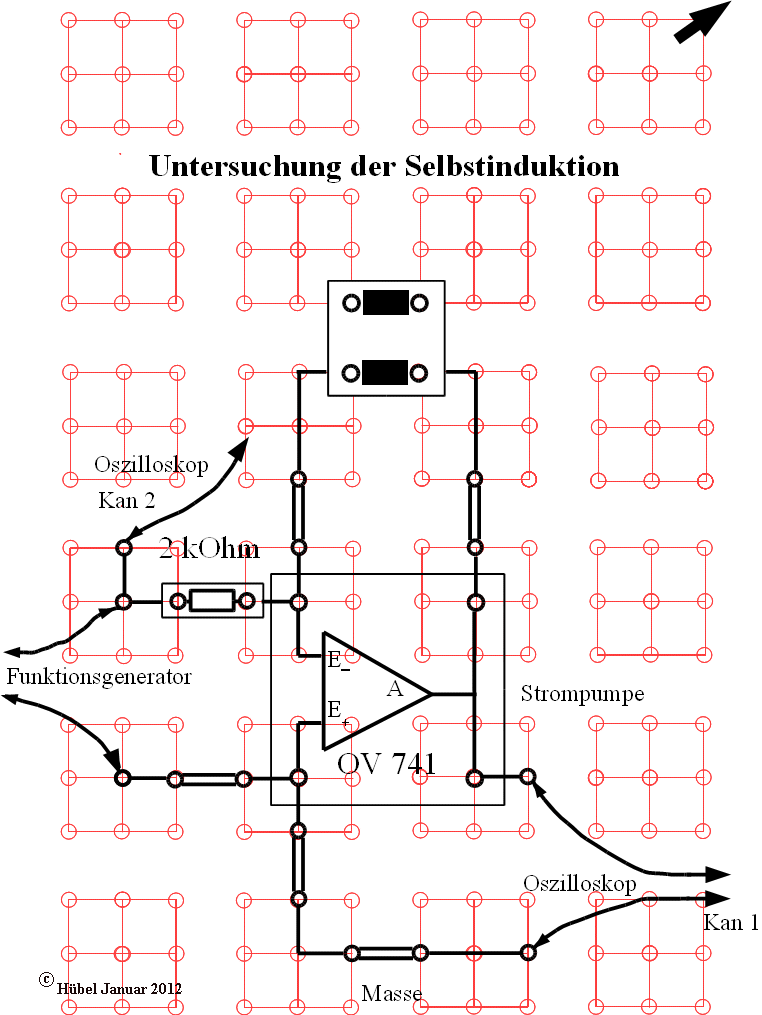Abb. 8: Aufbau der "Strompumpe" auf der Leybold-Rastersteckplatte mit Anschluss eines Funktionsgenerators und Oszilloskops für den Demonstrationsversuch (Auflageblatt). Als Spule wird eine "stromkompensierte Drossel" mit Ferritkern und zwei identischen Wicklungen (je 0,1 H; siehe Abb. 13) verwendet. Durch Kombination von zwei solchen Bauteilen kann man Induktivitäten bis 0,8 H erreichen. Alle anderen Bauteile auf dem Auflageblatt sind handelsübliche Stecker-Bauteile z.B. von Leybold. Mit Kanal 1 wird die (Selbst-)Induktionsspannung gemessen, mit Kanal 2 die dreiecksförmige Stromstärke. Alternativ kann die Selbstinduktionsspannung auch mittels der 2. Wicklung auf der SV-Spule gemessen werden. Beide Induktionsspannungen müsssen gleich groß sein, da ihre Ursache der sich ändernde magnetische Fluss im gemeinsamen Ferritkern ist.

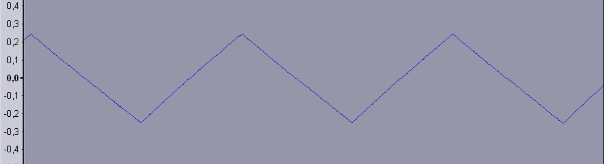	Abb. 9a:  Eingangsspannung in Abhängigkeit von der Zeit, aufgenommen mit der Soundkarte und angezeigt mit dem Programm AUDACITY.exe. Die Eingangsspannung in der Größenordnung von einigen V musste mit einem Spannungsteiler auf einige 10 mV heruntergeteilt werden. Vorsicht: Der Mikrophon-Eingang verträgt typisch eine Amplitude von 1 mV, der Line-In-Eingang von 1 V. Riskieren Sie keine Überlastung!
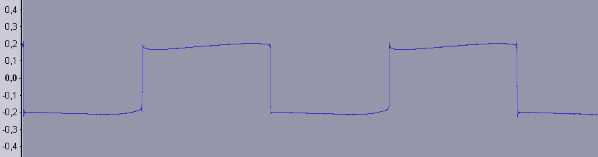	Abb. 9b: Ausgangsspannung als Maß für die Stromstärke bei kleiner Frequenz (ca. 50 Hz), aufgenommen mit der Soundkarte und angezeigt mit dem Programm AUDACITY.exe
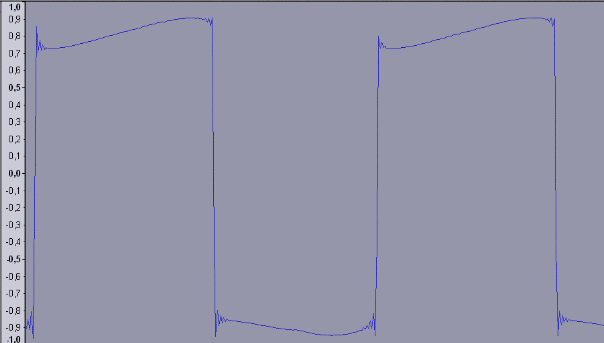	Abb. 9c: Ausgangsspannung als Maß für die Stromstärke bei großer Frequenz (ca. 300 Hz), aufgenommen mit der Soundkarte und angezeigt mit dem Programm AUDACITY.exe Es gibt leichte Abweichungen von der Konstanz der Stromstärke. Der relative Fehler ist allerdings gering. Gründe für den Fehler könnten sein: a) nicht ganz konstante Induktivität; bei einem Ferrit-Kern muss man damit rechnen, b) Einfluss des geringen ohmschen Widerstands der Spule (ca. 1,5 Ohm). Der Spannungsabfall würde sich am Ausgang zur Induktionsspannung (mit gleichem Vorzeichen wie diese) addieren, wie es auch beobachtet wird. Statt des erwarteten Rechteckssignals hätte das Signal damit allein schon eine gewisse "Dachschräge". c) endliche Bandbreiten des Operationsverstärkers und der Soundkarte. Selbst bei einem perfekten Rechteckssignal würde als Folge ein Überschwingen bei den scharfen Kanten beobachtet werden. Bei Verwendung eines guten Oszilloskop müsste dieser Effekt verringert sein. Vorsicht: Der Mikrophon-Eingang verträgt typisch eine Amplitude von 1 mV, der Line-In-Eingang von 1 V. Riskieren Sie keine Überlastung!

Ein Konzept zur Einführung des Gesetzes der Selbstinduktion bzw. der Induktivität L

1. Versuch: Vergleich des Zeitverlaufs von Strom I  und Spannung U_L: dreiecksförmiger Strom und (in guter Näherung) rechtecksförmige Spannung.: Solange sich der Strom gleichmäßig ändert, ist die Spannung  U_L konstant. Wenn die Stromstärke gleichmäßig steigt (fällt), ist die Spannung U_L konstant negativ (positiv). Vergleich mit Lenzscher Regel: Wie dort ist die Spannung U_L so gerichtet, dass sie ihrer Ursache (Stromanstieg bzw. -abfall) entgegenwirkt.

2. Versuch: Abhängigkeiten. Bei fester Frequenz wird die Amplitude der Steuerspannung bzw. des Ausgangsstroms verändert: Je schneller sich der Strom verändert, desto größer ist dem Betrag nach auch die Spannung U_L an der Spule.

3. Versuch: Quantitative Messung: Spannung U_L und Steigung des t-I-Graphen sind zueinander proportional.

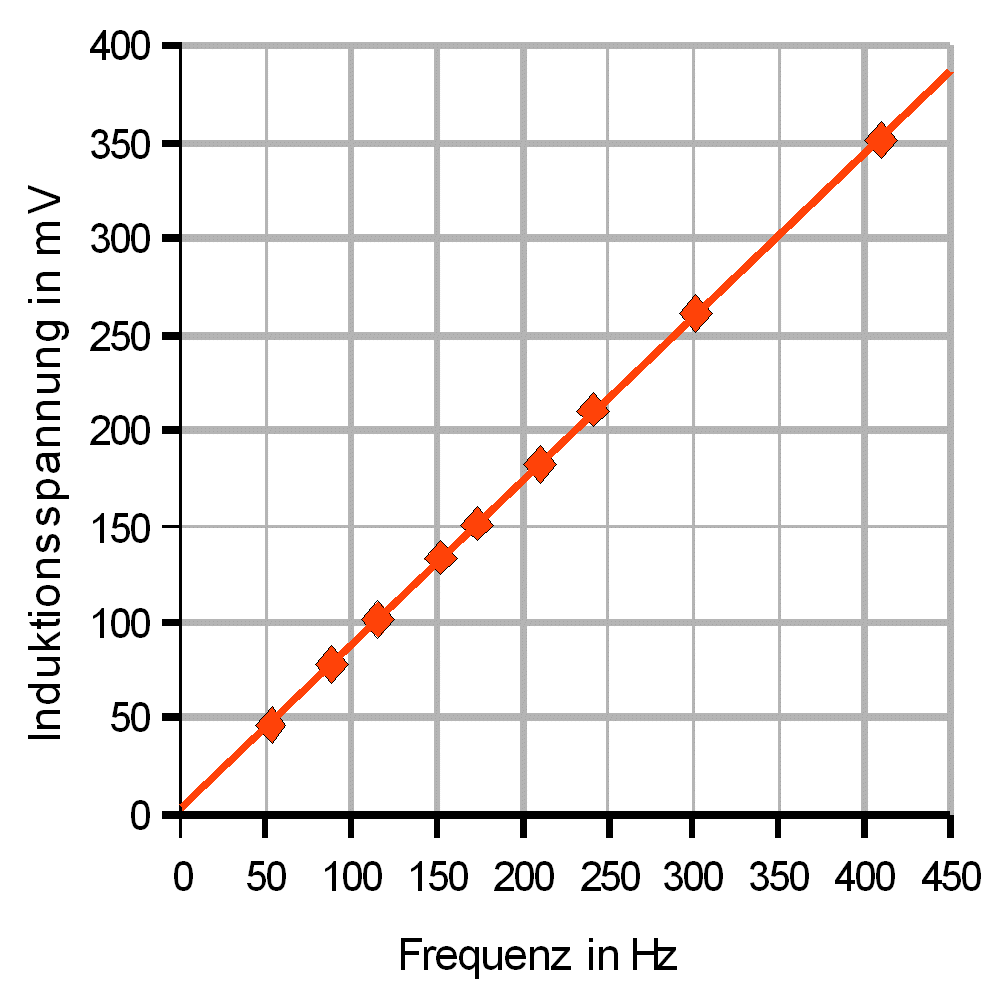	Abb. 10: 4. Versuch: Bei fester Eingangsspannung wird die Frequenz verändert. Der Versuch zeigt eine gute Proportionalität zwischen dem Betrag der Spannung UL und der Frequenz (Abb. 9). Das kennen die Sch schon von der gewöhnlichen Induktion: Je schneller sich das Magnetfeld in einer Spule ändert, desto größer ist der Betrag der Induktionsspannung.
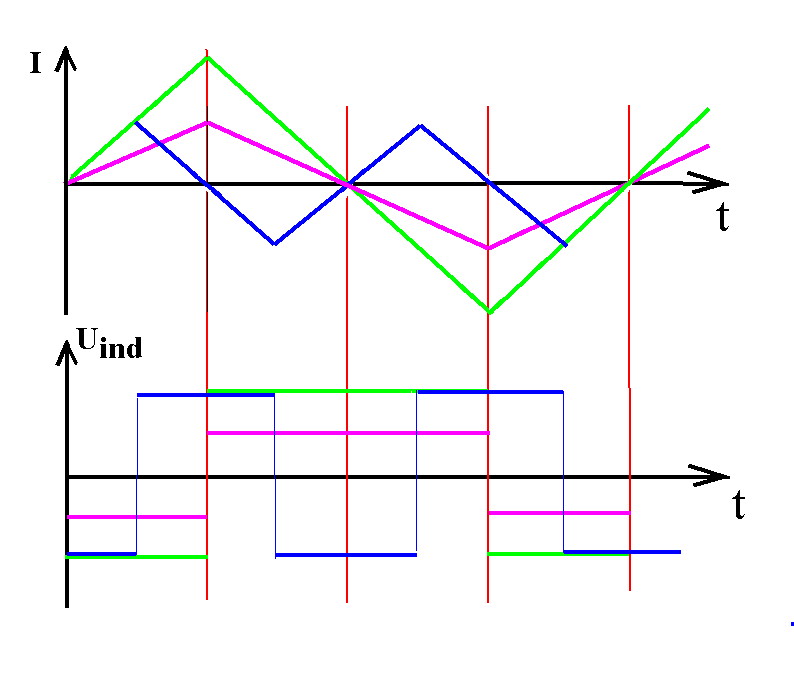	Abb. 11: Aber das Ergebnis lässt sich auch als Sonderfall von Versuch 3 deuten. Bei fester Stromamplitude (blaue und purpurne Kurve) ist die Steigung (Ableitung) des t-I-Graphen umso größer, je höher die Frequenz (blau). An einer Reihe von Zeichnungen entsprechend Abb. 11 erarbeiten sich die Sch diesen Sachverhalt.

5. Auswertung: Die Proportionalitätskonstante wird Induktivität L genannt. Die Sch ermitteln aus den Ergebnissen von Versuch 3 ihren Wert und ihre Benennung (sie sollten ca. L = 0,1 A/Vs erhalten).

6. Versuch: Bei einer festen Einstellung wird zunächst die Spannung U_L gemessen. Dann wird mit dem zweiten Kanal des Oszilloskops auch die vertraute Induktionsspannung an der zweiten Wicklung des Spulenbausteins gemessen. Beide Spannung sind (weitgehend und evtl. bis auf das Vorzeichen) identisch. Jetzt ist nun wirklich klar, dass es sich um einen Vorgang der Induktion handelt; sie findet statt, da sich das Magnetfeld im Ferritkern ändert. Da die zweite Wicklung auch fehlen könnte, heißt U_L Selbstinduktionsspannung. Der Begriff wird erläutert. Die Sch werden direkt darauf gestoßen, dass bei der Selbstinduktion die vorgegebene Stromstärke eine Spannung hervorruft!

Jetzt müssten die Sch motiviert und bereit sein, mit Hilfe einer theoretischen Rechnung bei einer langen Zylinderspule ohne Kern den Zusammenhang U_L = - L·ΔI/Δt bzw. U_L = - L·dI/dt zu verstehen. Für diesen Fall liefert diese dann auch eine Beziehung, wie sich L aus den Spulendimensionen berechnen lässt. Auf den allgemeineren Zusammenhang kann hin gelenkt werden, wenn jetzt statt eines Dreiecksstroms ein Sinusstrom durch die Spule geschickt wird.

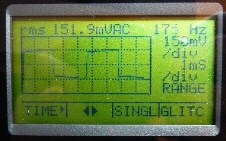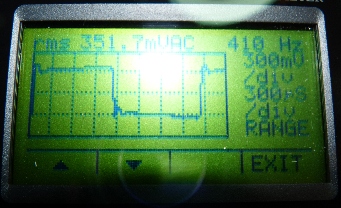
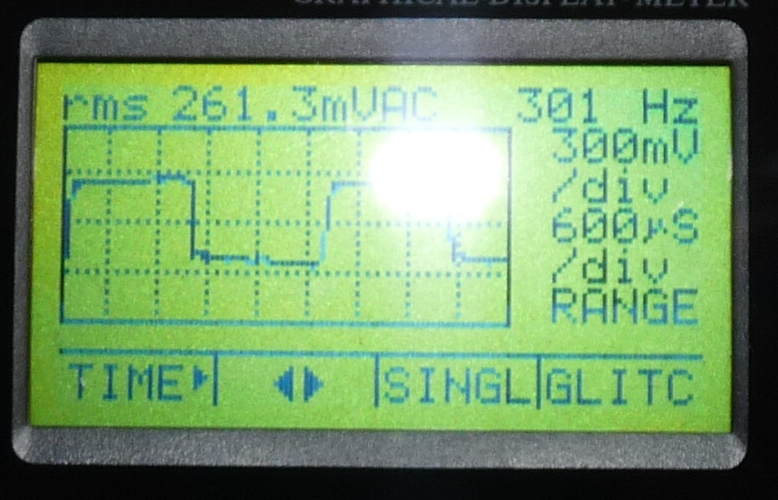
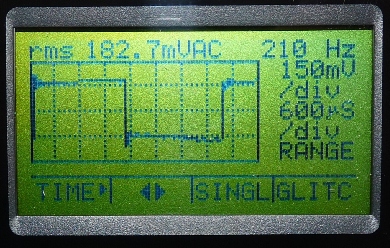
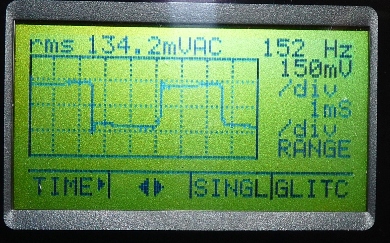
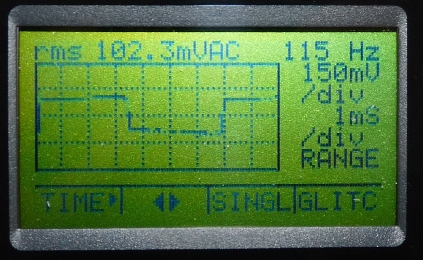
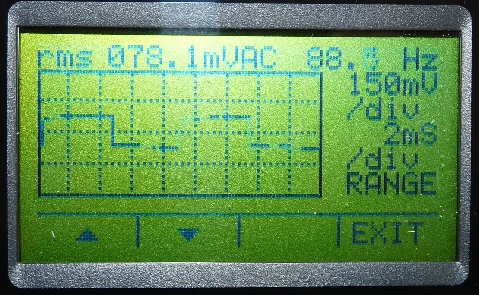
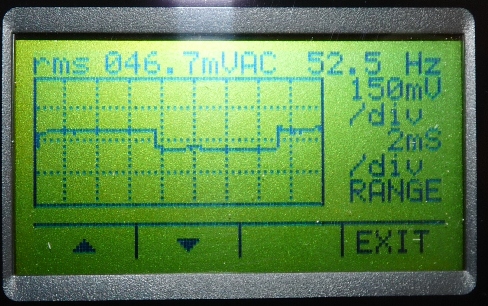
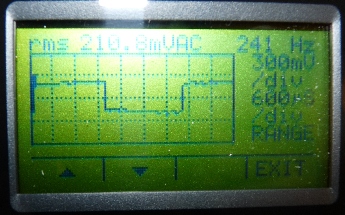
Abb. 12: Typische Anzeige der Selbstinduktionsspannung auf einem handheld-Oszilloskop. Hier werden komfortablerweise auch Frequenz und die rms-Spannung angezeigt. Sie waren Grundlage für die Abb. 9 .

Einsatz als Schülerversuch:

Als Messgerät wird die Soundkarte eines PCs verwendet. Sie zeigt wie in den Abb. 9 Kurvenformen, Periodendauern und (weniger genau) Amplituden. Dreieckssignale könnten zentral von einem Funktionsgenerator über die Verkabelung der Schülerarbeitstische erfolgen, oder mit einem einfachen Funktionsgenerator aus zwei Operationsverstärkern (Abb. 17), siehe unten.

Vorsicht: Der Mikrophon-Eingang verträgt typisch eine Amplitude von 1 mV, der Line-In-Eingang von 1 V. Riskieren Sie keine Überlastung!

Die Vorgehensweise ist sonst identisch; die theoretische Rechnung wird der Plenumsarbeit vorbehalten sein. Der 4. Versuch erfordert eine Umrechnung von Periodendauern in Frequenzen, weil mit der Soundkarte primär die Periodendauer (sogar sehr genau) abgelesen werden kann.

Die Bastler-Variante:

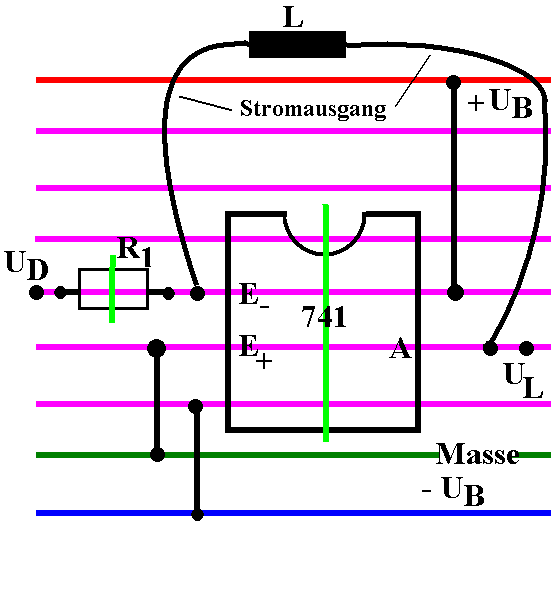
Abb. 13: Die gesteuerte Stromquelle in der Bastler-Variante; unten Layout für Lochstreifenplatine. Grün: Leiterbahn-Unterbrechungen; oben die "stromkompensierte Drossel" als Induktivität. Für den Versuch 6 bildet die Wicklung an den Stromanschlüssen die Feldspule, die zweite Wicklung (mit Induktionsspannung gekennzeichnet) die Induktionsspule.	Abb. 14: Dreiecksspannungsgenerator aus zwei OV (741); rechts die gesteuerte Stromquelle; siehe Anhang 2, Abb. 17

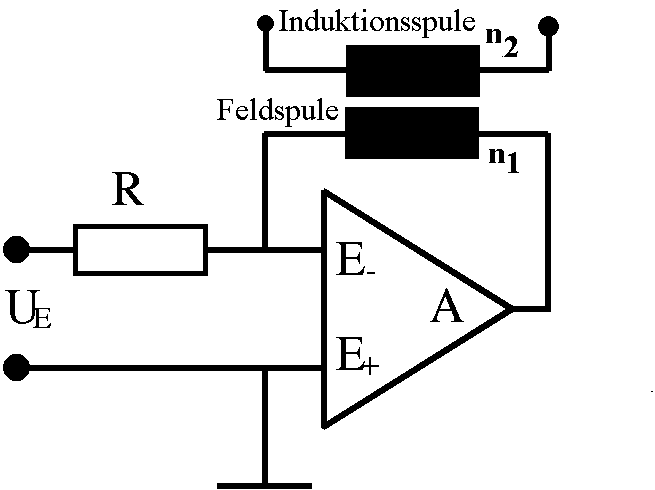
Untersuchung des Induktionsgesetzes im Schülerversuch

Abb.  15: Die "Strompumpe" arbeitet mit der gleichen Schaltung wie bisher. Die Spule dient jetzt als Feldspule mit einem linear veränderlichen Magnetfeld. Es kann eine beliebige Spule aus der Lehrmittel-Sammlung verwendet werden, dazu eine Induktionsspule mit größerer Windungszahl n2. (UA ist für diese Fragestellung belanglos und wird nicht gemessen.

Untersuchung des Induktionsgesetzes im Schülerversuch Es ist mittlerweile wohl üblich geworden, das Induktionsgesetz mit einem Dreiecksstrom sehr kleiner Frequenz herzuleiten, wobei eine (Sekundär-)Spule mit sehr großer Induktivität (z.B. mit 12 000 Windungen) verwendet wird, so dass der magnetfelderzeugende Strom und die Induktionsspannung mit einem Zeigermessinstrument geringer Anzeigeträgheit mit den Augen verfolgt werden kann. Ein entsprechender Schülerversuch scheidet aus, weil Funktionsgeneratoren mit Leistungsverstärker und große Spulen für arbeitsgleiche Schülerversuche fehlen. Weniger Schwierigkeiten gibt es mit folgendem Versuch: In der vorangehenden Schaltung wird die widerstandsarme Spule durch eine übliche Spule aus dem Lehrmittelhandel, z.B. mit n1 = 300 Windungen ersetzt. Sie wäre wegen ihres Innenwiderstands ungeeignet für den oben geschilderten Selbstinduktionsversuch. Aber der Funktionsgenerator (ohne Leistungsverstärker) erzeugt mit unserer "Strompumpe" einen dreiecksförmigen Strom und ein ebensolches Magnetfeld auch durch diese Spule, unabhängig von Innenwiderstand und Ausgangswiderstand des Generators (Feldspule). Eine Spule mit höherer Windungszahl n2 (vielleicht unterschiedliche für unterschiedliche Arbeitsgruppen) dient als Induktionsspule (sie wurde vorhin Sekundärspule genannt). Die Induktionsspannung wird mit der Soundkarte gemessen. Für manche Untersuchungen genügt auch ein Wechselspannungs-Multimeter. Ähnlich wie bei der Selbstinduktion finden die Schüler auch bei der gewöhnlichen Induktion: (1) Solange sich das Magnetfeld linear verändert, ist die Induktionsspannung konstant. (2) Die Induktionsspannung hat beim Steigung und Fallen des Magnetfelds umgekehrtes Vorzeichen. (3) Die Induktionsspannung ist umso größer, je schneller sich das Magnetfeld B ändert. (4) Die Induktionsspannung Uind ist prop. zu ΔI/Δt bzw. ΔB/Δt und zur Windungszahl der Sekundärspule (Flussdichte B).

Anhang 1:  Messwerte bei der Selbstinduktion mit einem billigen handheld-Oszilloskop

Abb.  16: Messwerte bei der Selbstinduktion mit einem billigen handheld-Oszilloskop

Anhang 2:

Ein Dreiecksspannungsgenerator aus zwei Operationsverstärkern

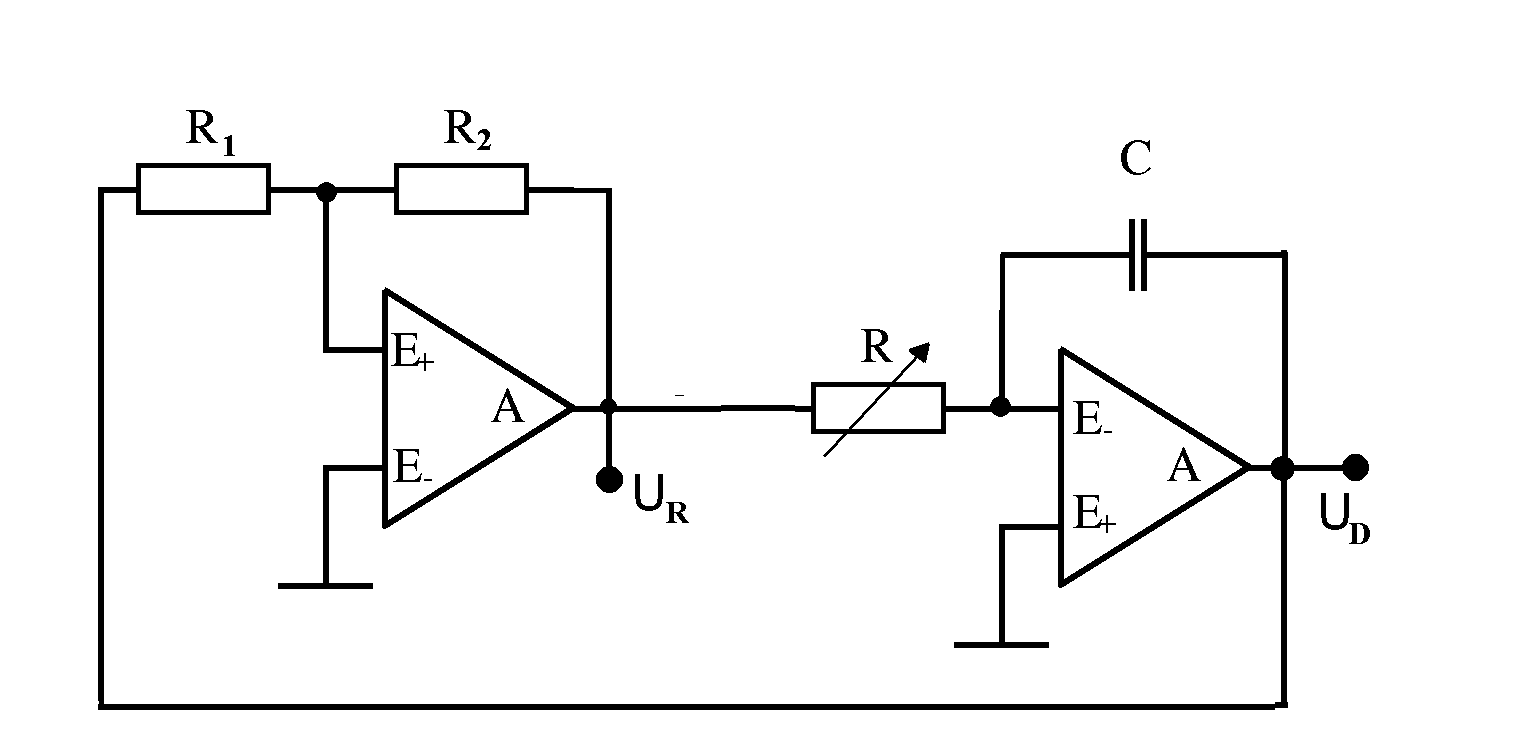Abb. 17: Ein einfacher Dreiecksspannungsgenerator aus zwei Operationsverstärkern (741); vgl. Tietze, Schenk, Halbleiterschaltungstechnik, Springer, 6. Auflage 1983, S. 463 Der rechte OV ist unser bekannter Ladungsmesser. Wenn ein konstanter Strom in ihn hineinfließt, wächst die Spannung am Kondensator linear an. Fließt ein gleich großer Strom in umgekehrter Richtung, fällt die Spannung am Kondensator linear. Das ist also ein "Rampengenerator". Er steuert selbst die Stromrichtung mittels des linken OVs. Dieser ist als Schmitt-Trigger geschaltet (Beachten Sie die Vertauschung der Eingänge E- und E+ !). Seine Ausgangsspannung hat entweder einen konstanten positiven Wert UR+ oder einen konstanten negativen Wert UR-. Das Umschalten geschieht, wenn der Eingang E+ auf Massepotenzial liegt. Das Potenzial seines Ausgangs sei jetzt UR+. Dann bilden die Widerstände R1 und R2 eine Spannungsteilerkette, die die Potenzialdifferenz UD + UR+ aufteilt. Wenn E+ auf Potenzial 0  ist (Umschaltsituation), gilt also (UD + UR+)/UR+ = (R1 + R2)/R2 bzw. UD = R1/R2·UR+ > 0. Dadurch ist die Amplitude bestimmt, die Frequenz durch das RC-Glied und das Widerstandsverhältnis: f = R2/4R1 · 1/R·C.   Analoges Ergebnis im zweiten Fall. R2 = 47 kOhm und R1 = 33 kOhm sind ein bewährtes Widerstandspaar. Für unsere Bastelvariante wurde C = 1 µF gewählt, für R ein Trimm-Poti mit maximal 10 kOhm Widerstand zur Einstellung der Frequenz.

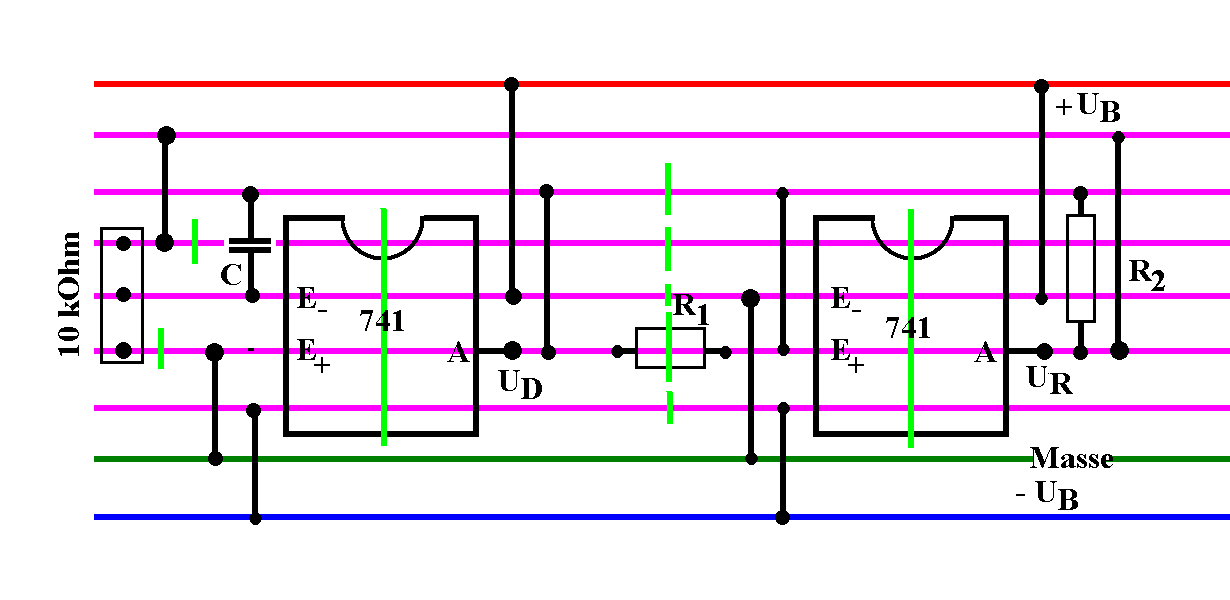Abb. 18: Verdrahtungsplan für ein Stückchen einer Lochstreifenplatine (gemäß Abb. 14). C = 1 µF, R2 = 47 kOhm und R1 = 33 kOhm; UD: Ausgang für Dreiecksspannung. Leiterbahn-Unterbrechungen sind hellgrün gekennzeichnet, die Leiterbahnen purpurfarben. Mit dem Poti links (10 kOhm) wird die Frequenz eingestellt. (Gegenüber Abb. 17 sind Rampengenerator und Schmitt-Trigger in umgekehrter Reihenfolge angeordnet)

Anhang 3:

Ein aus dem Rahmen fallendes Beispiel: Ein Strom-Spannungswandler. Sehr kleine Ströme, z.B. von einer Photodiode, kann man nachweisen, indem man zwischen die Stromanschlüsse einen sehr großen ohmschen Widerstand R₂ schaltet, z.B. 10 MOhm. Durch ihn muss der kleine Strom I ebenfalls fließen. Das geht nur dadurch, dass eine Spannung U_A = I·R₂ entsteht. Sie kann zwischen Ausgang und Masse als Maß für I gemessen werden. 0,1 µA ruft dann im Beispiel bereits eine Ausgangsspannung von 1 V hervor.

In diesen Text flossen auch Kenntnisse ein, die ich durch Herrn Prof. Dr. D. Heuer kennengelernt habe.