Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierigkeiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2021

Schülerversuche mit einem preiswerten Spulenbaustein

Hinweis:   Korrekte Darstellung mathematischer Symbole unter Netscape / Mozilla ab Version 6

Z.B. bei Reichelt electronic gibt es eine stromkompensierte Drossel (Bestellnr. 42H3205, ca . 2 Euro; Hersteller: Radiohm) mit den Daten L0 = 0,1 H +/- 30 %, R = 1,5 Ohm pro Wicklung (!). Auf einen Baustein mit 4 Stück 4mm-Steckern montiert ergibt sie einen preiswerten Spulenbaustein mit zwei Wicklungen ("blaue Drossel"). Kombiniert man die beiden Wicklungen und zwei solcher Bausteine, hat man die Induktivitäten 0,1 H, 0,2 H, 0,4 H  und 0,8 H zur Verfügung. Es lassen sich damit leicht Schwingkreise hoher Güte und Induktivitäten im Schülerversuch untersuchen. Der geringe Innenwiderstand lässt sich mit Spulen aus dem Lehrmittelhandel schwer erreichen und macht diesen Spulenbaustein einzigartig.

Abb. 1: Spulenbaustein aus einer stromkompensierten Drossel, die auf ein Plättchen mit 4 Stück 4-mm-Steckern montiert wurde, geeignet zum Aufstecken auf die Leybold-Rastersteckplatte

Allerdings muss man in Kauf nehmen, dass wegen des Ferritkerns L nicht unbedingt konstant ist, wie man das bei einer Luftspule erwartet. Wegen der besonderen Hysteresis-Kurve gelingen Induktionsversuche nicht in jedem Fall so, wie man es in der Schule gerne hätte.

Die folgenden Versuche lassen sich - abgewandelt - natürlich erst recht mit Spulen aus dem Lehrmittelhandel durchführen, die aber  bei vergleichbarer Induktivität deutlich höhere Widerstände haben. Schwingkreise mit diesem Spulenbaustein sind also relativ wenig gedämpft; sie werden weit vom Kriechfall entfernt betrieben.

Versuche:

• Nachweis des Energieerhaltungssatzes bei einem elektromagnetischen Schwingkreis
• Messung von L
• Thomson-Formel eines elektromagnetischen Schwingkreises
• Resonanzkurve eines elektromagnetischen Schwingkreises / Messung von L
• Ein-/Ausschaltvorgänge

Beschaltung solcher Spulenbausteine (Vgl. Tabelle unten):

Wie üblich addieren sich Induktivitäten getrennter Bausteine, die in Reihe geschaltet sind. Mit zwei solcher Bausteine kann man also 0,2 H erreichen. Schaltet man die beiden Wicklungen auf dem gemeinsamen Ringkern in Reihe, erhält man 0,4 H. Für eine Spule auf einem Toroid-Kern gilt nämlich L = µ_r · µ₀ · n²A/(2·r·π) mit der Windungsfläche A, der Windungszahl n, dem Toroidradius r und der relativen Permeabilität µ_r (falls es eine solche gibt). Zwei solcher Wicklungen in Reihe geschaltet ergeben also die doppelte Windungszahl und damit 4-fache Induktivität. Schaltet man die beide Wicklungen auf dem gemeinsamen Kern parallel, muss man das Induktionsgesetz bemühen. Einerseits fließt dann durch jede Wicklung nur der halbe Strom. Andererseits addieren sich im Kern die Magnetfelder beider Wicklungen. Beide Effekte heben sich gegenseitig auf, so dass die Induktivität nicht geändert wird: L = 0,1 H.

Versuche:

Abb. 2: Ansicht mit einer Anordnung an der Deutschen Schule Algarve. Hier wurde ein Präzisionsgleichrichter (siehe Abb. 4) eingesetzt, aufgebaut mit einem Operationsverstärker und einer Si-Diode. Unser Eigenbau-OV wurde mit zwei Batterien versorgt. Für den OV wäre eine professionelle Lösung empfehlenswert, z.B. mit dem Leybold-OV-Baustein. In den folgenden Abbildungen sieht man die Auflageblätter für die Rastersteckplatten, die einen sicheren Aufbau durch die Schüler gewährleisten und mehr Überblick verschaffen. Abb. 3: Einfachere Anordnung, die auch das Prinzip der Messmethode besser zeigt. Es sollte hier eine Schottky-Diode eingesetzt werden, um Probleme mit der Diodenkennlinie zu mindern.	1. Experimenteller Nachweis des Energieerhaltungssatzes bei einem elektromagnetischen Schwingkreis Es wird ein bekanntes Verfahren eingesetzt: Die magnetische Energie einer stromdurchflossenen Spule wird unter Ausnutzung der Induktion in die elektrische Energie eines Kondensators 1/2 · C · U2 umgewandelt (Abb. 2). Diese wird durch die entstehende Ladespannung U des Kondensators gemessen. a) Trägt man dann die Ladespannung U in Abhängigkeit vom Spulenstrom I auf entsteht eine Ursprungsgerade, aus der man abliest, dass die magnetische Energie in der gleichen Weise von der Stromstärke I abhängt wie die elektrische Energie von der Ladespannung U, also quadratisch. Die Proportionalitätskonstante wird unter Einfügung eines entsprechenden Faktors 1/2 als Induktivität L definiert: Emagn  = 1/2 · L · I2 . b) Setzt man Energieerhaltung voraus, muss also gelten:   1/2 L · I2  =  1/2 C · U2  bzw. L = C · (U/I)2 . Damit hat man eine relative Messung von L, deren Genauigkeit im wesentlichen durch die Genauigkeit der C-Kenntnis bestimmt ist. Allerdings gibt es Einwände: Ohmsche Widerstände sorgen für Energie-Verluste, insbesondere in der Spule, aber auch in der Diode. Die Diode selbst sperrt weitgehend unter einer bestimmten Knickspannung (Si: ca. 0,6 V, Schottky-Diode ca. 0,15 - 0,3 V; eine Ge-Diode erscheint günstiger). Gängige Ge-Dioden sind aber für Stromstärken von typisch maximal 5 mA ausgelegt. Beachtet man dies, kann man mit Ge- oder Schottky-Dioden schon recht brauchbare Ergebnisse erzielen (Abb. 3). In der I-U-Kennlinie erkennt man allerdings das Abschneiden unterhalb der Knickspannung. Das kann in vielen Fällen verkraftet werden. Bessere Ergebnisse erhält man mit einem Präzisisionsgleichrichter mit einer Operationsverstärker-Schaltung (Abb. 2, 4) . Hier sind I und U wirklich proportional zueinander. (In der Abbildung ist eine primitive Eigenbauvariante für den OV verwendet. Man sollte lieber einen kommerziellen Operationsverstärker-Baustein aus dem Lehrmittelhandel verwenden. Für die Leybold-Rastersteckplatte werden Auflageblätter verwendet, die einen sicheren, leicht kontrollierbaren und übersichtlichen Schaltungsaufbau ermöglichen.)
Abb. 4: Einsatz eines Präzisionsgleichrichters mit einem Operationsverstärker, entsprechend Abb. 2. Er sorgt für eine lineare Diodenkennlinie. Der Ladestrom des Kondensators wird dann nicht abgeschnitten, wenn die Spannung unter die Knickspannung der Diode gesunken ist.	Abb. 5: Beschaltung für die Induktivität 0,4 H. A und B sind die externen Anschlüsse.
Abb. 6: Ladespannung U in Abhängigkeit vom Spulenstrom I; dient auch zur Messung von L	Eine fast perfekte Ursprungsgerade für die Energieumwandlung von magnetischer in elektrische Energie bei Verwendung des Präzisionsgleichrichters! Sie zeigt: 1. Die magnetische Energie in der stromdurchflossenen Spule hängt in der gleichen Weise von der Stromstärke ab wie die elektrische Energie des Kondensators von der Ladespannung, die sich einstellt, wenn die magnetische Energie vollständig in die elektrische Energie des Kondensators übergeführt wird. Also: Wegen Eel  prop U2  gilt auch Emagn prop I2. Die Proportionalitätskonstanten sind C/2 bzw. L/2. 2. Aus der Steigung 0,26 V/mA = ΔU/ΔI = U/I   wird hier geschlossen: L/C = 0,262 V2/mA2 = 0,0676 V2/mA2 = 0,0676·106 V2/A2 Bei C = 2·10-6 F folgt also L = 2·0,0676 H = 0,135 H

2. Relativ-Messung von L (wie oben):

Für einen Kondensator mit nominell 1 µF Kapazität ergab sich so ca. L = 0,1 H, bei einem Wert 0,1 H nach Datenblatt.

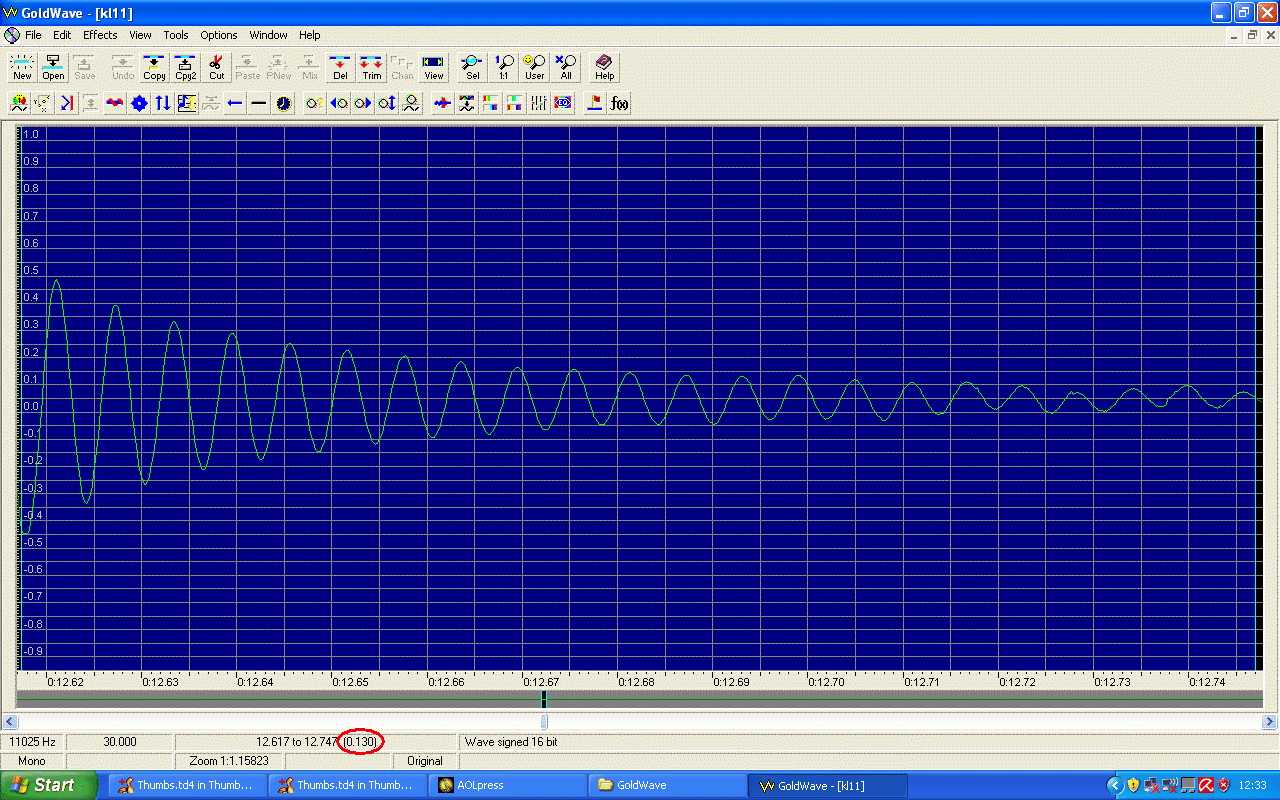
3. Gedämpfte elektromagnetische Schwingung Einem elektromagnetischen Schwingkreis aus dem Spulenbaustein und einem Kondensator (1 µF - 47 µF) wird mittels einer Monozelle und eines Tasters kurzzeitig Energie zugeführt. Bis diese aufgebraucht ist, führt der Schwingkreis eine elektromagnetische Schwingung aus. Sie kann mit einem Oszilloskop, einem PC-Messinterface oder mit der Soundkarte eines PCs demonstriert werden. Wir verwenden u.a. die Soundkarte und das Programm GOLDWAVE (Abb. 7, 8). Mit GOLDWAVE lässt sich auch die Schwingungsdauer messen. Wegen der recht hohen Güte des Schwingkreises klingt die Amplitude relativ langsam ab (Abb. 7). Die Schaltung ist hier auf einer Leybold-Rastersteckplatte aufgebaut, wobei ein Auflageblatt einen sicheren Aufbau durch die Schüler garantiert. Da auch bei Verwendung einer Monozelle leicht Amplituden von mehreren V entstehen können, empfiehlt es sich den Mikrophon- oder LineIn-Eingang des PCs durch Verkleinerung der Spannung mit einem Potenziometer zu schützen (Abb. 8). Vorsicht: Der Mikrophon-Eingang verträgt typisch eine Amplitude von 1 mV, der Line-In-Eingang von 1 V. Riskieren Sie keine Überlastung!

Abb. 7: gedämpfte Schwingung, aufgenommen mit der Schaltung von Abb. 8, gemessen mit der Soundkarteeines PC und dem Programm GOLDWAVE (oder anderen). Beachten Sie die relativ schwache Dämpfung! In der roten Ellipse wird die Zeit zwischen 2 Marken abgelesen.

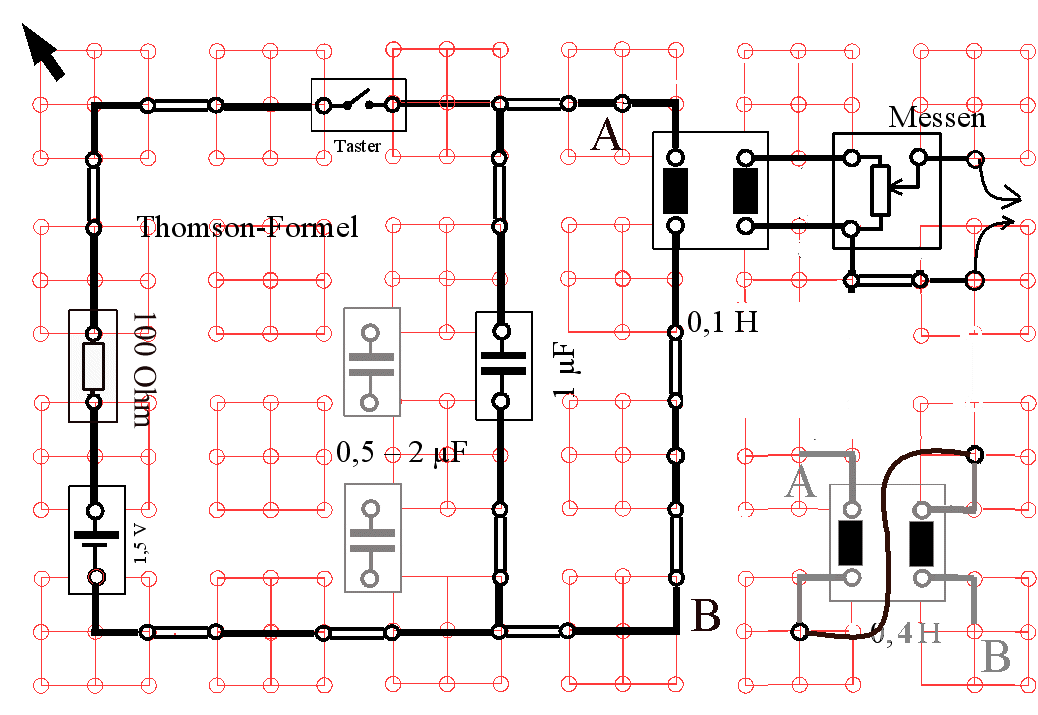4. Überprüfung der Thomson-Formel für die Eigenfrequenz des Schwingkreises bei einer gedämpften Schwingung Schaltet man 2 gleiche Kondensatoren in Reihe oder parallel, dann hat man neben dem einfachen Kondensator mit der Kapazität C die Kapazitäten C/2 und 2·C zur Verfügung, also eine Verdoppelung bzw. Vervierfachung. Entsprechend hat man gemäß obigem Schaltungsvorschlag die Induktivitäten L, 2·L und 4·L zur Verfügung. Mit dem Programm GOLDWAVE (oder ähnlichen) kann auf dem Bildschirm die Schwingungsdauer gemessen werden (zur Verbesserung der Genauigkeit misst man 5 oder 10 Perioden aus). Zunächst wird L konstant gelassen. Die Schüler werden zu einer Hypothese animiert, wie sich doppelte (4-fache) Kapazität auswirken könnte. Der Versuch zeigt es dann sofort: Erst 4-fache Kapazität führt bei konstanter Induktivität zur doppelten Schwingungsdauer. Entsprechend gehen die Schüler bei der Induktivität vor: Bei konstanter Kapazität führt erst 4-fache Induktivität zur doppelten Schwingungsdauer: ganz klar ein quadratischer Zusammenhang. Obwohl m.E. bei diesem Versuch das Verhalten bei Verdoppelung oder Vervierfachung von L oder C im Vordergrund steht, lässt sich der Versuch auch quantitativ auswerten. Es empfiehlt sich wieder, den Mikrophon- oder LineIn-Eingang des PCs durch Verkleinerung der Spannung mit einem Potenziometer zu schützen (Abb. 8).

Abb. 8: Auflageblatt für die Leybold-Rastersteckplatte zur Erzeugung gedämpfter Schwingungen. Die Induktivität L und die Kapazität C lässt sich durch Umstecken der Bauteile leicht in Schritten vom Faktor 2 verändern.

	5. Überprüfung der Thomson-Formel für die Eigenfrequenz des Schwingkreises bei einer ungedämpften Schwingung mittels Resonanz Mit Hilfe eines Funktionsgenerators einstellbarer Frequenz wird die Resonanzfrequenz des Schwingkreises aus Kapazität C und unserem Spulenbaustein gesucht. Wegen der hohen Güte des Schwingkreises ergibt sich eine scharfe Resonanzfrequenz. Zur Messung der Amplitude kann ein Oszilloskop, ein Computer-Messinterface oder wieder die Soundkarte eingesetzt werden. Im letzten Fall sollte der Eingang der Soundkarte wieder geschützt werden. Die Beziehung ω2 = 1/(L·C) wird für die unterschiedlichen Werte von L und C quantitativ untersucht. Statt des Funktionsgenerators kann auch ein Experimentier-Interface (z.B. FORPHYS mit AVISE) verwendet werden.
Abb. 9: Erzwungene Schwingung; Erregerschwingung aus Funktionsgenerator mit beliebiger Kurvenform; Nachweis der erzwungenen Schwingunen durch ein Oszilloskop. Hier wird kapazitive Kopplung mit einem möglichst kleinen Kopplungskondensator (0,1 µF) verwendet (Vgl. Resonanzkurven beim Parallelschwingkreis). Anordnung an der Deutschen Schule Algarve.
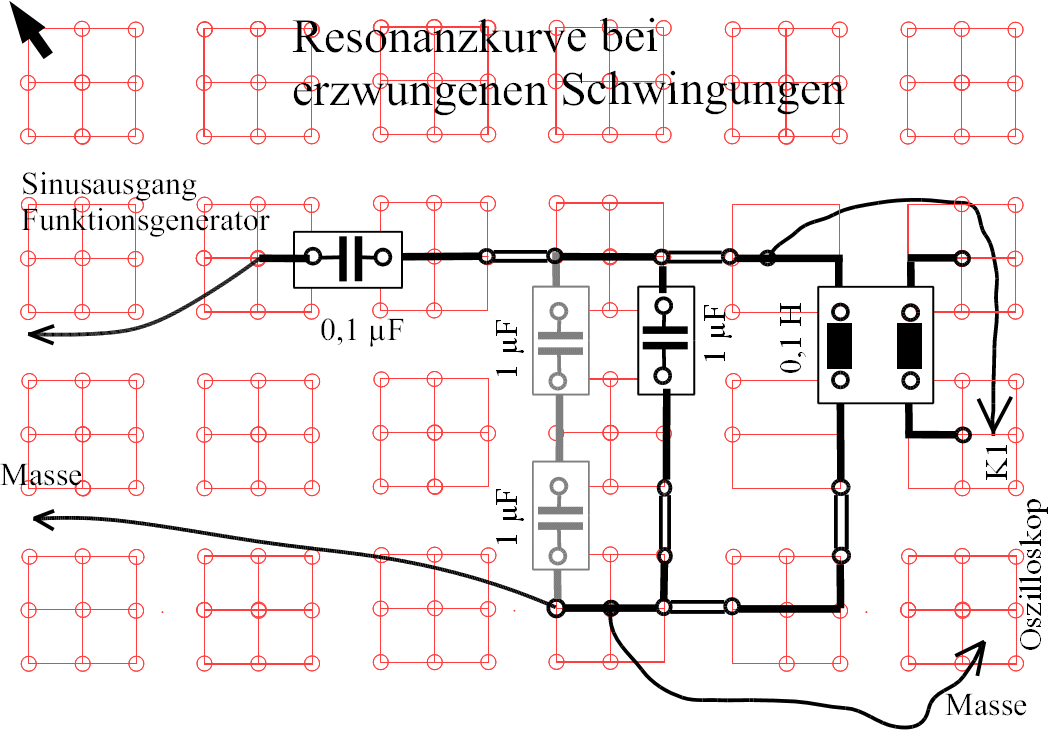
Abb. 10: Auflageblatt für die Leybold-Rastersteckplatte zur Erzeugung von erzwungenen Schwingungen

	6. Gedämpfte Schwingung, angeregt durch ein Rechteckssignal aus einem Funktionsgenerator. Auch so lässt sich - entsprechend Versuch 4 - der Einfluss von L und C testen. Statt des Funktionsgenerators kann auch ein Experimentier-Interface (z.B. FORPHYS mit AVISE) verwendet werden. Ebenso für den Nachweis der Schwingung. Dafür ist aber auch wieder die Soundkarte des PCs geeignet.
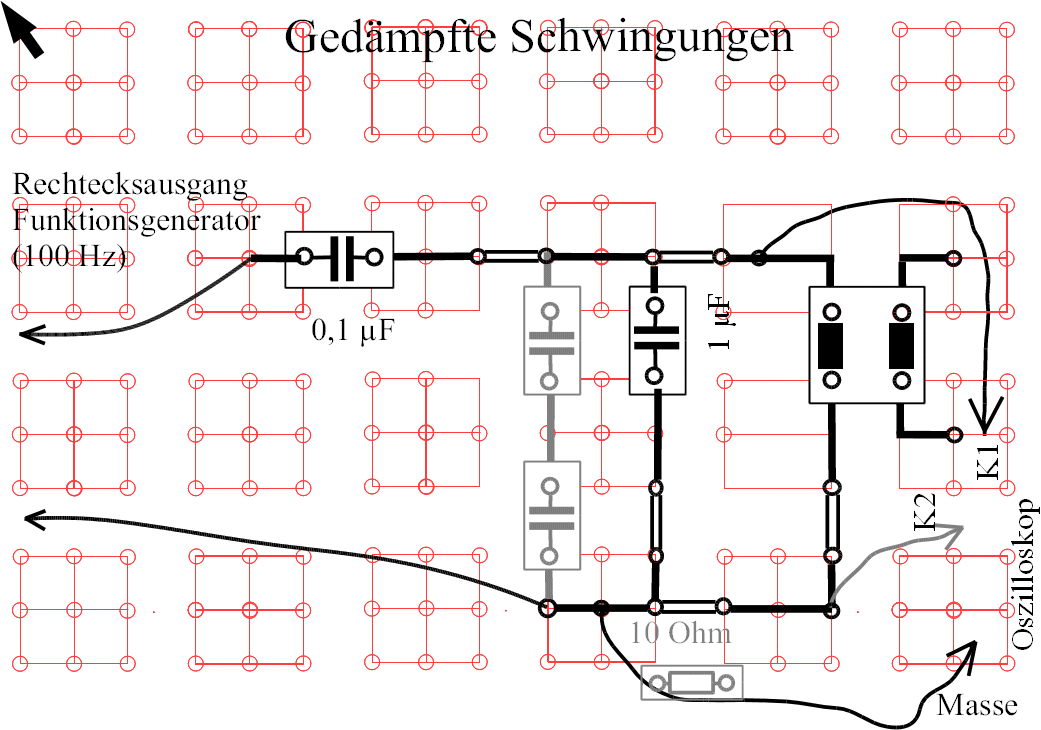
Abb. 11: Auflageblatt für die Leybold-Rastersteckplatte zur Erzeugung gedämpfter Schwingungen durch Anregung mit einem Rechteckssignal aus dem Funktionsgenerator
Abb. 12: Auflageblatt für die Leybold-Rastersteckplatte zur Erzeugung gedämpfter Schwingungen; Funktionsgenerator und Oszilloskop können durch ein Messinterface (z.B: FORPHYS mit AVISE) bzw. die Soundkarte des PCs ersetzt werden

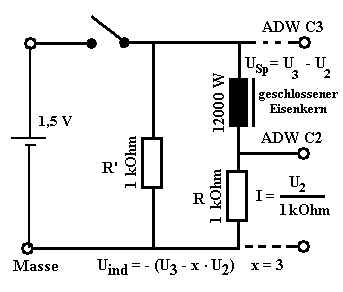7. Ein-/Ausschalt-Vorgänge Ein-/Ausschalt-Vorgänge werden in der Schule durch die zwei didaktisch wichtigen Bedingungen dominiert: Spule Stetigkeitsbedingung "Die Stromstärke macht keine Sprünge" Spannungsbedingung "Die Induktionsspannung muss sich so einstellen, dass sie dem Induktionsgesetz genügt und die Stetigkeitsbedingung für die Stromstärke bewirkt." Für die Messung von Stromstärke und Selbstinduktions-Spannung im Demonstrationsversuch hat sich die nebenstehende Schaltung bewährt. Mit ihr lässt sich die Stetigkeitsbedingung und die Spannungsbedingung gut überprüfen. Durch Veränderung von R' kann man nämlich die Selbstinduktions-Spannung leicht verändern. Man braucht in der Regel ein Messinterface, da die Selbstinduktions-Spannung nicht direkt zugänglich ist und erst aus der Spulenspannung U3 - U2 und dem Spannungsabfall I·Ri errechnet werden muss. Bei der Spule der Zeichnung beträgt  Ri  = 2 kOhm. Von der Spulenspannung muss also der Spannungsabfall an 2 kOhm + 1 kOhm subtrahiert werden. Deshalb also x = 3. Weil der Innenwiderstand der Spule Ri bei Verwendung der "blauen Drossel" sehr klein ist, kann die Schaltung so dimensioniert werden , dass der Spannungsabfall an ihm vernachlässigbar ist (es geht schon mit z.B. R = 100 Ohm). Dann kann auf ein Messinterface verzichtet werden. Die Selbstinduktions-Spannung ermittelt dann ein Oszilloskop mittels U3 - I·R , wobei wahlweise I (eigentlich I·R) oder Uind angezeigt werden kann (siehe unten).

Abb. 13: Schaltung aus dem Buch "Schülerexperimente mit Mikroprozessor und PC" vom Verfasser der Homepage (ADW C3 bedeutet dort AD-Wandler Kanal C3)

Abb. 14: Ergebnis: Selbstinduktions-Spannung, leider invertiert, und wichtige Einstellungen Abb. 15: Entsprechend Abb. 13 Abnahme der zwei Spannungen für das Oszilloskop. Hier wird ein regelbarer Widerstand  R' verwendet. Abb. 16: Ergebnis: Induktionsstrom Abb. 17: Entsprechend Abb. 13 Abnahme der zwei Spannungen für das Oszilloskop. Hier wird ein fester Widerstand  R' verwendet (siehe unten). Abb. 18: Verfälschtes Eingangssignal (vom 600-Ohm-Ausgang des Funktionsgenerators) Abb.  20: unverfälschtes Eingangssignal (vom Leistungsausgang des Funktionsgenerators) Abb. 19: Die Einstellung ist ersichtlich. Es sollte jedoch der niederohmige Ausgang des Leistungsverstärkers verwendet werden. Andernfalls führt ein ansteigender Strom wegen des Ausgangs-Widerstands von 600 Ohm zu einer veränderten Spannung (Abb. 18). Das wiederum hat Einfluss auf die Höhe der Spitzenspannung. Wählt man andererseits den niederohmigen Ausgang, dann ist zur Spulen-Widerstandskombination immer der Ausgangswiderstand (quasi 0 Ohm) parallel geschaltet. Ein zusätzlicher Widerstand R' hat dann keinerlei Einfluss mehr (Abb. 20). Den (didaktisch bedeutsamen) Einfluss von R' kann man offenbar nur zeigen, wenn man, z.B. handgesteuert mittels eines Schalters, die Stromquelle mit ihrem kleinen Innenwiderstand für den Ausschaltvorgang abtrennt. Hat man dies vor, empfiehlt sich doch wieder der Einsatz eines Messinterfaces. Statt des Funktionsgenerators kann auch ein Experimentier-Interface (z.B. FORPHYS mit AVISE) verwendet werden. Dann sind echte Schülerversuche in parallelen arbeitsgleichen Gruppen (Partnerarbeit) möglich. Der kleine Innenwiderstand erlaubt dann relativ langsame Messungen (charakteristische Zeit τ = L/R = 0,1/1,5  s = 0,06 s ). Allerdings braucht man dann für die Strommessung einen vergleichbar kleinen Widerstand, der T wiederum erniedrigt und schwer herzustellen ist. Dann muss wie oben der innere Spannungsabfall berücksichtigt werden. Vergleich mit anderen Drosseln aus dem Elektronik-Handel (z.B. Reichelt electronic, entsprechend der angegebenen Bestellnummern): Bei Spulen und Schwingkreisen sind zwei Zeiten wichtig: die Schwingungsdauer T und die charakteristische Zeit  τ. Die charakteristische Zeit τ ist ein Kriterium für das Einsetzen des Kriechfalls in einem Schwingkreis. Gedämpfte Schwingungen sind nur bei genügend kleiner charakteristischer Zeit möglich. Der Kriechfall tritt ein, wenn für den Ohmschen Widerstand des Schwingkreises gilt R > 2 √L/C. Faustregel: Gefahr des Kriechfalls um so größer, je kleiner L und je größer C, wenn R konstant. Schwingungsdauer T (in für die Schule hinreichender Genauigkeit) T = 2π √(L·C) = 2π √τ·τc charakteristische Zeit (Zeitkonstante) τ  der Spule τ = L/R charakteristische Zeit (Zeitkonstante) τc  des Kondensators τc = R·C Kriechfall für R > 2 √L/C Die charakteristische Zeit (Zeitkonstante) τ  bestimmt den Zeitmaßstab bei Ein-/Ausschaltvorgängen. Sie definiert auch ein Maß für die Messrate bei Messungen mit einem Messinterface. Erst, wenn τ in der Größenordnung von 1 s  ist, sind on-line-Messungen (z.B: mit dem Programm GRAFTERM) sinnvoll.

Baustein	Reichelt Bestellnummer	Widerstand Ri	Kriechfall für R > 2·√L/C	Schwingungsdauer T mit C = 1 µF	charakteristische Zeit τ = L/R der Spule *)	charakteristische Zeit τc= R·C des Kondensators	Abweichung 1/16π2  (T/τ)2	Eigenfrequenz	Induktivität L	Bemerkung
"blaue Drossel"	42H3205	1,5 Ohm	ca. 600 Ohm	ca. 2 ms	ca. 66 ms	1,5 µs	0,000006	ca. 500 Hz	0,1 H	extrem geringer Innenwiderstand; fern vom Kriechfall; jeweils verdoppelte Induktivitäten durch Beschaltung leicht erreichbar
Übertrager 1 : 4	NFU 1-4	4,6 Ohm	ca. 300 Ohm	1,0 ms	ca. 5 ms	4,6 µs	0,000212	1 kHz	primär 0,025 H	fern vom Kriechfall
Übertrager 1 : 4		115 Ohm	ca. 1300 Ohm	4,5 ms	ca. 4 ms	115 µs	0,006483	222 Hz	sekundär 0,51 H	sekundär ca. 16-fache Induktivität; stark gedämpfte Schwingungen
Übertrager 1 : 2	NFU 1-2	sekundär 30 Ohm	ca. 600 Ohm	ca.  2 ms	ca. 3 ms	30 µs	0,002250	0,5 kHz	sekundär 0,1 H	Windungszahl sekundär verdoppelt => vierfache Induktivität; brauchbar entfernt vom Kriechfall
zweibeinige Ferrit-Drossel 150 mH	L -11P 150 M	205 Ohm	ca. 800 Ohm	2,5 ms	ca. 0,8 ms	205 µs	0,067348 = 6 %	400 Hz	0,156 H	näher am Kriechfall siehe Abb. 21
zweibeinige Ferrit-Drossel 100 mH	L -11P 100 M	155 Ohm	ca. 600 Ohm	2 ms	ca. 0,6 ms	155 µs	0,060063	500 Hz	0,1 H	näher am Kriechfall
zweibeinige Ferrit-Drossel 47 mH	L -11P 47 M	73 Ohm	ca. 400 Ohm	1,4 ms	ca. 0,6 ms	73 µs	0,028346	730 Hz	0,047 H	recht nahe am Kriechfall; bei Verwendung von zwei Bauteilen weitere Induktivitäten erreichbar
große Leybold-Drossel		280 Ohm	(C = 100 µF:)   5 kOhm (C = 1 µF: )  50 kOhm	C = 100 µF: ca. 1,6 s C = 1 µF: ca.0,16 s	ca. 2,25 s	28000 µs	0,000031 0,003111	0,6 Hz bzw. 6 Hz	630 H	langsame Schwingungen; langsame, mit dem Auge verfolgbare Ein-/Ausschaltvorgänge

Abweichungen der Eigenfrequenz vom ungedämpften Fall sind bei Schulgenauigkeit vernachlässigbar.

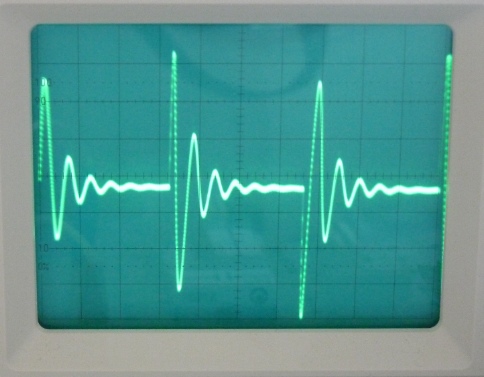Abb. 21: Anregung eines Schwingkreises mit C = 1 μF und der zweibeinigen Ferritdrossel (L = 0,15 H) mit einem 100 Hz-Rechteckssignal aus dem Funktionsgenerator. Wegen des deutlich höheren ohmschen Widerstands (ca. 200 Ohm) klingt die Schwingung deutlich schneller ab als in Abb. 7. Auch mit der Soundkarte lässt sich die Schwingungsdauer messen und nach L auswerten.

ω₀ = 1 /  √(L·C)    L·C = 1/ω₀² = T₀² /4π²     L = T₀²/(4·π²·C)

T₀ = 2π √(L·C)        ω₀ =  2π /T₀

ω = √ [1 / (L·C) - 1/4 τ² ] = √ [ω₀²  - 1/4 τ² ] = ω₀√ [1   -   1/(4ω₀²τ²) ] = ω₀ √ [1   -   C·L·R²/4·L² ] =  ω₀ √ [1   -   1/4 τ_c/τ ] = ω₀ √ [1   -   1/(4·4·π²) T₀²/τ²]

Tabelle zur Beschaltung des Spulenbausteins:  ( zurück )

Beschaltung des Ferrit-Spulenbausteins (Abb. 1)	L
einfache Spule	L0
2 gleiche Spulen parallel auf gleichem Ferritkern (Toroid): in jeder Windung halber Strom, aber B-Feld im Kern durch doppelte Windungszahl erzeugt	L0
2 gleiche Spulenbausteine parallel	0,5·L0
2 gleiche Spulenbausteine in Reihe, entspricht Spule mit doppelter Windungszahl und doppelter Länge (L prop n2/l)	2·L0
2 gleiche Spulen auf gleichem Ferritkern in Reihe (entspricht Variante in Abb. 8)	4·L0
2 gleiche Spulenbausteine in Reihe, wobei die beiden Wicklungen entsprechend der vorangehenden Zeile verbunden sind	8·L0

Alle Versuche und Schaltungen sind nach bestem Wissen mitgeteilt. Eine Gefährdung von Schülern oder des PCs wird nicht erwartet; dass sie nicht eintritt, liegt ganz im Verantwortungsbereich des Nutzers. Der Autor übernimmt keinerlei Haftung.

( März 2016: Zeichensatz geändert)