Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierigkeiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Strom-Modelle

"A battery or generator is like your heart: it moves blood, but it does not create blood." W. Beaty

1. Schüler glauben, dass eine Stromquelle Ladungen produziert und wieder aufsaugt, oder gar, dass sie irgendetwas mit dem Namen "Strom" erzeugt, was aus dem einen Pol herausströmt und im anderen wieder verschwindet. Wir wissen, dass sie dies "Ladungen" nennen müssten, die aber nicht verschwinden, sondern nur durch den Stromkreis und die Stromquelle hindurchgepumpt werden.

Oder sie glauben, dass irgendetwas aus der Stromquelle herausströmt, von einem "Verbraucher" verbraucht wird und danach eben nicht mehr zur Stromquelle zurückkehrt. Diese Vorstellung ist gar nicht so falsch, wenn man den "Strom" der Schülervorstellung ersetzt durch "Energie":

Energie strömt aus der Stromquelle heraus, wird "verbraucht" (natürlich: in andere Energieformen umgewandelt) und kehrt nicht mehr zur Stromquelle zurück. Wäre es nicht eine Hilfe für die Schüler, wenn man ihnen sagen würde: Bleibt bei eueren Vorstellungen, nur verwendet bitte den offiziellen Namen "Energie" dafür! Nicht für "Strom" muss die monatliche Rechnung bezahlt werden, sondern für die Energie, die das EVU liefert. Strom ist etwas anderes, etwas Abstrakteres, nämlich das Fließen von elektrischen Ladungen, die im Stromkreis eben nicht verloren gehen, sondern immer im Kreis herumgepumpt werden.

Vgl. Hinweise zum Thema "geschlossener Stromkreis" aus der 8. Klasse

a) Die geringe Driftgeschwindigkeit ( ca. 1 mm/s) und die Elektronendichte der Leitungselektronen (ca. 1 Leitungselektron pro Atom; Dichte der frei beweglichen Leitungselektronen in Cu ≈ 8.10²⁸ m^-3) ermöglichen eine Abschätzung der von den Elektronen transportierten kinetischen Energie. Diese ist viel zu gering!

b) Im Stromnetz fließt Wechselstrom. In der Zeit einer Periode können die Leitungselektronen nur geringste Strecken zurücklegen ( Abschätzung: 1 mm/s . 1/100 s = 10^-5 m). Wie sollten sie aus dem E-Werk die Energie "holen"? Die wirkliche Situation deutet sich schon in einer anderen Meinung an, nämlich, dass die Energie "mit Lichtgeschwindigkeit" von Elektron zu Elektron weitergegeben werde. Richtig daran ist, dass der Energietransport durch das beteiligte elektromagnetische Feld erfolgt, nicht durch die Ladungen.

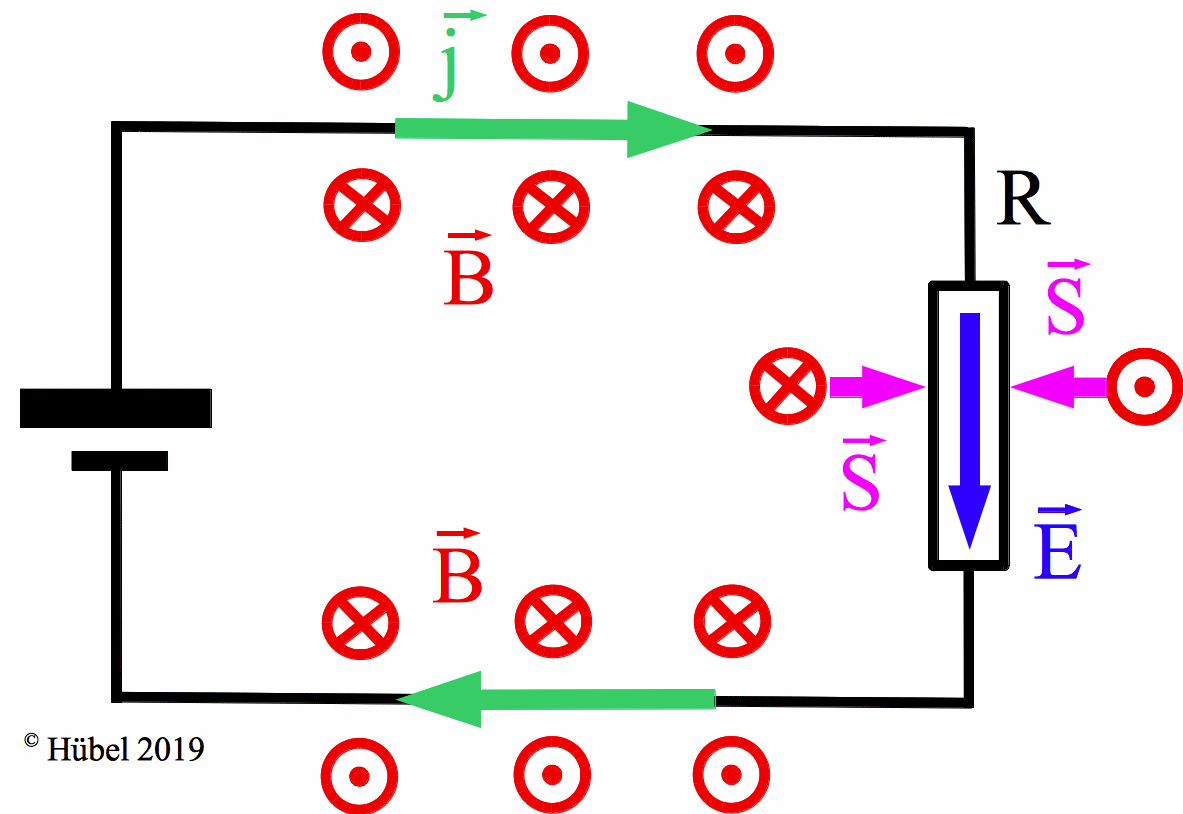
c) Die Elektrodynamik lehrt: Der Energietransport wird durch den Poynting-Vektor S = E x B beschrieben. Danach strömt die Energie (vor allem) durch die den Leiter umgebende Luft senkrecht zu E und B, also z.B. senkrecht in die Wandung eines zylinderförmigen Ohmschen Widerstands hinein. In einem idealen Leiter könnte überhaupt keine Energie transportiert werden, weil in ihm wegen des verschwindenden Ohmschen Widerstands kein elektrisches Feld herrschen könnte.

Stellvertretend für andere Elektrodynamik-Lehrbücher ein Zitat nach Becker, Theorie der Elektrizität, Teubner 1964, S. 154:

"Wir fragen nun, wie die dort in Wärme umgewandelte elektrische Energie überhaupt an diese Stelle gelangt. Daß sie dorthin durch die Leitungselektronen im Draht transportiert wird, erscheint von vornherein äußerst unwahrscheinlich. Dazu kommt noch, daß sich die Elektronen wegen ihrer großen Zahl auch bei den größten Stromdichten nur mit einer relativ kleinen mittleren Geschwindigkeit (einige cm/s) durch den Draht hindurchbewegen.  

.... Somit fließt an den Stellen des Stromsystems, an denen elektrische Energie verbraucht wird, diese Energie aus dem Feld in den Draht hinein, wobei die Dichte dieser Energieströmung durch den Poynting-Vektor S gegeben wird. Entsprechend fließt, wie man sich in gleicher Weise klarmachen kann, an den Stellen, an denen eingeprägte Kräfte wirksam sind, Energie aus dem Stromsystem heraus und in das Feld hinein."

Punkt c) wird man den Schülern sicher verschweigen, er bewahrt den Lehrer aber vor falschen Argumenten.

Noch klarer wird dies bei der Induktion in einer Leiterschleife durch ein sich änderndes Magnetfeld.

Dabei ist klar, dass der Energiestrom-Vektor nicht eindeutig durch den Poynting-Vektor S = E x B (bis auf Maßsystemfaktoren) beschrieben wird. Aus der Herleitung von S folgt, dass man zu S jeden beliebigen Vektor addieren kann, dessen Divergenz im betrachteten Raumbereich verschwindet. Das hat dazu geführt, dass bei statischen Feldern, wo S = E x B  zu merkwürdigen Aussagen zu führen scheint, die Bedeutung von S angezweifelt wurde. Dabei ist aber klar, dass man beide Probleme beseitigt, wenn man jeweils über einen bestimmten Raumbereich integriert. Dann liefern alle Varianten für den Energiestrom-Vektor das gleiche Ergebnis und die merkwürdigen Aussagen treten nicht auf. Weil S = E x B  eng mit dem Impulsstrom-Vektor und einem Drehimpulsstrom-Vektor zusammenhängt, die durch die relativistische Kovarianz enger festgelegt sind, sieht man in der Regel keinen Anlass, S = E x B  zu ergänzen.

Vgl. auch einen Internet-Beitrag von Backhaus: Der Energietransport durch elektrische Ströme und elektromagnetische Felder in verschiedenen Darstellungen. Ein Beispiel für das Zusammenspiel zwischen Erfahrung und Konvention bei der physikalischen Begriffsbildung, Udo Backhaus, Fachbereich Physik der Universität Osnabrück

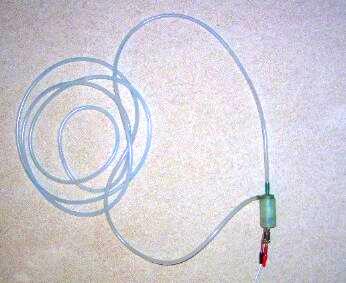
"Stromquelle" bzw. Pumpe ist eine (gebrauchte) Scheibenwischerpumpe aus einer Autowerkstatt, zu betreiben mit max. 12 V Gleichspannung. An sie wird aus dem Baumarkt oder Gartencenter ein mehrere Meter langer durchsichtiger Plastikschlauch (6 mm) angeschlossen. Luftblasen im Füllwasser des Schlauchs zeigen den Wasserstrom an. Vielleicht steht auch ein Turbinenmodell zur Verfügung. Mit Hilfe eines Netzteils wird die "Pumpenstärke" der "Stromquelle" eingestellt. Mit Lebensmittelfarbe kann das Wasser eingefärbt werden, dann sind die Luftblasen besser sichtbar.

Mit Hilfe des meterlangen Schlauchs lassen sich große Höhendifferenzen überwinden. Es ist evident, dass sie keinerlei Einfluss auf den Wasserstrom haben, selbst bei noch so schwacher Pumpe. Die Pumpe im Foto konnte spritzend  nur ca. 40 cm Höhendifferenz überwinden; das entspricht also der potenziellen Energie, die sie dem Wasser mitgeben kann. Sie konnte aber beliebige Höhendifferenzen überwinden, weil die potenzielle Energie, die ein Wasserteilchen beim Hochsteigen gewinnt, durch ein anderes beim Herabsteigen wieder abgegeben wird: Wie es auch die Theorie für den elektrischen stationären Strom zeigt, spielt potenzielle Energie bei solchen Vorgängen keinerlei Rolle!

• Im Rohrsystem ist Wasser (Ladungen) stets vorhanden.
• Es wird durch eine Pumpe immer im Kreis herumgepumpt (Umwälzpumpe) und
• transportiert dabei Energie.
• Die Turbine (Birnchen) entspricht einem (Energie-) Verbraucher, der Energie entzieht und nach außen abgibt. (Analog: ein Heizungskörper, entsprechend einem Birnchen).
• Ein Widerstand entspricht einer Engstelle, die Strom durchlässt, den Strom aber auch begrenzt (Doppelfunktion eines Widerstands).
• Zwei Engstellen hintereinander begrenzen den Stromfluss stärker als eine von ihnen.
• Zwei Engstellen parallel lassen mehr Strom hindurch als eine von ihnen allein.
• Die Stromstärke entspricht der gepumpten Wassermenge pro Zeiteinheit (Ladungsmenge pro Zeiteinheit).
• Mit der Spannung misst man die "Pumpenstärke" der Stromquelle.
• Ein Spannungsabfall an einem Widerstand entsteht, weil sich zwischen den beiden Enden des Widerstands eine Druckdifferenz aufbaut.
• Ein Wasserhahn (besser: Drosselventil) begrenzt den Strom oder sperrt ihn ganz und entspricht damit einem Schalter.
• Die starren Rohre der Rohrleitungen "führen" den Wasserstrom, ähnlich wie Oberflächenladungen auf den elektrischen Leitungen den elektrischen Strom "führen". Während des Einschaltvorgangs hat sich der Strom die Oberflächenladungen selbst erzeugt, ausgehend von der Stromquelle.

Zwei Pumpen hintereinander vermögen trotz der behindernden Engstelle einen größeren Strom als eine von ihnen hindurch zu pumpen. Bei zwei Pumpen parallel beginnt das Modell zu versagen: Es fließt nicht mehr Strom durch den Stromkreis, aber jede der Pumpen muss weniger leisten und wird länger geschont, d.h. hat eine längere Lebensdauer oder benötigt zum Betrieb weniger Energie. Zwei Pumpen entgegengesetzt hintereinander geschaltet, heben sich in ihrer Wirkung gegenseitig auf. Zwei Pumpen entgegengesetzt parallel geschaltet, laufen leer und werden evtl. zerstört, weil sie sich gegenseitig Strom (ohne weitere Begrenzung) immer nur zupumpen.  Ein Spannungsabfall an hintereinander geschalteten Widerständen ist in der Analogie als Druckdifferenz an den Engstellen deutbar. Mit dem Druck zu argumentieren ist aber problematisch, weil er den Schülern in diesem Stadium möglicherweise unbekannt und vielfach auch später unverstanden ist.

Hinweis: Der Hinweis auf das Wasserleitungssystem ist für die Schüler unter Umständen wenig hilfreich, da ja nach Schülermeinung das Wasser dort "von allein fließt", sobald man nur den Hahn aufdreht. Das Wasserleitungssystem braucht also nach Schülermeinung keine Pumpe und ein Hahn hat eher die Aufgabe, einen Strom fließen zu lassen als ihn abzusperren. Es besteht auch eher die Neigung, "die Wasserleitung" als etwas aufzufassen, das Wasser (entsprechend den Ladungen) zu liefern, und nicht einfach, vorhandene Ladungen fließen zu lassen. Der Schüler sieht keinen geschlossenen Stromkreis, weil er das Klimasystem (Meer, Sonne, Regen) nicht als Teil des Stromkreises (Pumpe) ansieht. Konkretes Modell eines geschlossenen Stromkreises

Bitte achten Sie auch darauf, dass der Wasserstromkreis auch "hinten geschlossen" ist; Zeichnungen wie in vielen Schulbüchern, wo die Pumpe ("Stromquelle") weggelassen ist, sind für den Anfangsunterricht abzulehnen!

4. Das "Paternoster-Modell" ("Ketten-Modell") beschreibt das stromtransportierende Medium wie eine Kette von zusammenhängenden Perlen oder Paternoster-(Aufzugs-)Kabinen. In der "Stromquelle" wird diese Kette in Bewegung versetzt; dennoch bewegt sich die Kette als Ganzes. Kettenglieder verlassen auf der einen Seite die "Stromquelle" und werden auf der anderen Seite wieder ersetzt. Überall bewegen sich die Kettenglieder mit gleicher Geschwindigkeit. Höhenunterschiede (entsprechend zusätzlichen Potenzialdifferenzen) haben keinerlei Einfluss auf die Bewegung bzw. den Energietransport; energetisch spielt allein die Stromquelle eine Rolle, insofern sie Energie zuführt, und Reibungsmechanismen, die Energie abführen. Durch dieses Modell werden wesentliche Aspekte eines Stromkreises modellmäßig beschrieben. Allerdings ist hier die einzige beteiligte Energie mechanische Energie in den bewegten Kettengliedern, während die mechanische Energie im elektrischen Stromkreis vernachlässigbar ist und stattdessen mit dem Transport von elektromagnetischer Energie gekoppelt ist. (Im Modell ist sicher keine potenzielle Energie als Folge der Gravitation beteiligt, kaum kinetische von der gemeinsamen Kettenbewegung, vielleicht potenzielle Energie als Folge der interatomaren Kräfte: all dies ist schwer zu überschauen. Um solche Diskussionen zu vermeiden, bewährte sich die Annahme einer nicht dehnbaren Kette; dann verrichtet die Stromquelle direkt Arbeit gegen die Reibungskräfte.)

Man würde wieder ein überflüssiges und komplizierendes Element ins Spiel bringen, wenn man "Höhenenergie" diskutieren würde!

5. In Schulbüchern sind Modelle eines durch Zwischenreservoirs unterbrochenen (also in gewissem Sinn offenen - nicht zu verwechseln mit dem "offenen Stromkreis") Wasserkreislaufes in Gebrauch, entsprechend etwa der Trinkwasserversorgung mit einem Wasserturm und (offenen) Zwischenspeichern. Pumpen haben die Aufgabe, Wasser in den Hochbehälter zu pumpen. 2 Pumpen hintereinander geschaltet schaffen die doppelte Höhe wie eine von ihnen. Der erreichten Höhendifferenz entspricht eine Druckdifferenz, die der Anlass dafür ist, dass hintereinander geschaltete Turbinen mit Energie versorgt werden. Je mehr Turbinen hintereinander geschaltet sind, desto geringer ist bei gleicher Höhe des Hochbehälters (Druckdifferenz) der Wasserstrom durch sie (Wassermenge pro Zeiteinheit). Je größer die Höhe des Hochbehälters (Druckdifferenz), desto mehr Turbinen können eingesetzt werden, ohne dass sich der Strom verändert. Der scheinbare Vorteil dieses Modells liegt in der Veranschaulichung des Drucks (Spannung) durch Höhendifferenzen. Es versagt ebenfalls bei hintereinander geschalteten, gegeneinander arbeitenden Pumpen (eine dritte sollte gar nichts mehr leisten können). Der Zusammenhang zwischen Lageenergie / Arbeit und Spannung nach U = W/Q ist scheinbar klarer. Unklarer ist die Rolle der Turbinen als Strombegrenzer; allenfalls müsste Wasser in Zwischenreservoirs gespeichert werden. Entspricht ein solcher Rückstau der Realität? Würde der Rückstau nicht wieder für einen schnelleren Abfluss sorgen? Physikalisch ist aber auch klar: für den Strom ist allein die Pumpe zuständig. Sie allein bestimmt die Stromstärke durch eine vorgegebene Engstelle (Widerstand); Lageenergie (Höhenenergie) spielt überhaupt keine Rolle, weil die Energie, die auf der einen Teilstrecke aus der Höhenenergie gewonnen wird, auf einer anderen Teilstrecke wieder verloren geht. Und: wer kann schon überblicken (gar noch: welcher Schüler?), wie sich ein stationärer Zustand in dem Wasserstromkreis mit den Zwischenreservoirs ausbildet?

Die Zwischenreservoirs führen ein problematisches Element ein. Es hängt mit der Verletzung des Prinzips der Ladungserhaltung zusammen: Würde das Wasser nicht schnell genug abfließen, würde sich das Wasser also in einem Zwischenreservoir stauen, dann wäre oberhalb die Stromstärke größer als unterhalb. Es könnte aber auch sein, dass von oben nicht genug Wasser nachkommt. Dann würde die untere Turbine aus Wassermangel stehen bleiben, es sei denn, man füllt die Zwischenreservoirs von vornherein soweit auf, dass "lokale" Schwankungen keine Rolle spielen. Vielleicht bildet sich mit der Zeit ein stationärer Zustand aus, bei dem sich die Wasserhöhen in den verschiedenen Reservoirs gerade so eingestellt haben, dass ein konstanter Strom fließt. Aber: wer kann das schon überblicken (gar noch: welcher Schüler?). Man könnte also auch sagen, dass dieses Modell das Augenmerk zu stark auf die Einstellung des stationären Zustands richtet, während dieser im elektrischen Stromkreis in allen praktischen Fällen längst abgeschlossen ist.

6. Es ist möglich, eine Spannung U als Potentialdifferenz zu definieren: U = ΔW/Q . Das geht aber nur beim Vorliegen eines elektrostatischen (Potential-)Felds. Bei der Induktion liegt aber meist eine Situation vor, wo ein Strom fließt, aber keine Spannung (im Sinne einer Potentialdifferenz) existiert (es liegt ein elektrisches Wirbelfeld vor). Das ist besonders auffällig bei der Supraleitung, aber auch bei der Induktion in Ringleitern. Hier wird ein elektrisches Wirbelfeld erzeugt, das Kräfte auf die Ladungen ausübt, die deshalb einen Ringstrom erzeugen. Man kann die Situation aber entschärfen, wenn man von U = ΔW/Q  ausgeht, wobei ΔW die Arbeit zur Verschiebung der Ladung zwischen den beiden Punkten ist, zwischen denen die Spannung U besteht. Dann braucht man nicht über die Wegunabhängigkeit der Arbeit (also das Vorliegen eines Potentials) sprechen und erfasst die Situation der Elektrostatik und des elektrischen Wirbelfelds, wie bei der Induktion. Vgl. Spannungsmodelle

Es muss darauf hingewiesen werden, dass als Ursache eines Stromes nicht immer eine Spannung nötig ist. Bei Wechselstromkreisen mit einer Spule oder einem Kondensator und beim elektromagnetischen Schwingkreis gibt es Zeitpunkte, wo gerade bei verschwindender Spannung die Stromstärke maximal ist. In Supraleitern kann ein Strom u.U. jahrelang ohne Spannung fließen. Umgekehrt ist beim Spannungsabfall an einem Widerstand die Spannung gerade die Folge eines Stroms.

7. Als Modell für einen elektrischen Widerstand hat sich im Modell des geschlossenen Wasserstromkreises eine Engstelle bewährt. Sie hat die Doppelfunktion, einen Strom hindurchzulassen, aber auch - zusammen mit der "Pumpenstärke" der Stromquelle - seine Stärke zu bestimmen: Der Widerstand begrenzt den Strom. Wagenschein macht Vorschläge, wie man die Funktion solcher Engstellen Schülern anschaulich klarmachen kann: Schüler stehen auf einem Schlauch: je mehr Schüler, umso stärker wird der Wasserstrom begrenzt.

M.E. hat es keinen Sinn, bei der Einführung in die Physik (7./8. Kl.) Stromkreise mit mehreren Schaltern und Birnchen zu besprechen, ohne den Schülern ein primitives Modell von Stromkreisen mitzugeben. Dazu müssen unbedingt Spannungsquelle (entspr. Pumpe), Strom (entspr. Wasserstrom in einem geschlossenen Kreislauf) und Widerstand (entspr. Engstelle/Heizkörper) qualitativ plausibel gemacht werden. Erst dann werden die "Schaltungen" behandelt und können von den Schülern verstanden werden.

8. Blutkreislauf: instruktiv, aber mit Schwächen

"A battery or generator is like your heart: it moves blood, but it does not create blood." W. Beaty

Der Stromquelle entspricht das Herz als Pumpe, den Ladungen in den Leiter das Blut in den Arterien oder Venen, die Kapillaren in den Organen, wo sauerstoffreiches Blut in sauerstoffarmes Blut übergeht, den "Engstellen" von Widerständen oder Lampen. Es wird "Energie" benötigt, um das bereits überall vorhandene Blut durch die Kapillaren bzw. überall vorhandene Ladungen durch die Lampen oder Widerstände hindurchzupumpen. Insofern kann dieses Modell gute Hilfe leisten.

Der Blutkreislauf hat seine Tücken als physikalisches Modell, weil er in Wirklichkeit aus zwei Teilstromkreisen besteht, dem Körperkreislauf und dem Lungenkreislauf.

( August 2019: B-Feld-Richtung in Zeichnung korrigiert; toter Link entfernt)