|
Der stationäre
elektrische Strom in der Schule
|
| In diesem Text wurde die offizielle Theorie des stationären
Stromes in die Sprache der Schulphysik übersetzt. Er stützt sich
auf W. Panofsky, M. Phillips, Classical electricity and
magnetism, Addison-Wesley Publishing Company, 2. Auflage
1962, S. 118 - 122 und viele andere Standard-Lehrbücher der
Elektrodynamik. Diese Theorie ist in weiteren Texten
dargelegt, z.B. auch hier. Viele
Überlegungen aus der Theorie des stationären Stroms müssen in der
Schule verschwiegen werden, aber das, was mit den Schülern
erarbeitet wird, sollte der Theorie nicht widersprechen. |
Das sollte m.E. ein Schüler im Physik-Unterricht über den
elektrischen Stromkreis erfahren: (Die Sätze in den eckigen Klammern
dienen nur zur Erläuterung für den Lehrer)
- Chemische "Kräfte" in einer galvanischen Zelle, einer Batterie oder
einem Akku können wie eine Pumpe Ladungen in Bewegung setzen, die
überall im Stromkreis bereits vorhanden sind.*)
- In einem geschlossenen Stromkreis bildet sich nach kurzer Zeit ein
zeitlich konstanter (stationärer) Strom aus.
[ Nur in dieser Übergangsphase kommt es zu einem Wechselspiel zwischen
getrennten Ladungen, der Stromstärke I (der Stromdichte j) und dem
sich bildenden elektrischen Feld E, so dass schließlich überall im
Stromkreis außerhalb der Stromquelle das ohmsche Gesetz gilt:
j = σ·E ; σ
elektrische Leitfähigkeit **) ] .
- Im unverzweigten Stromkreis ist dann die Stromstärke überall gleich
groß, Anzeichen dafür, dass nirgendwo Ladungen verloren gehen oder
hinzukommen.
[ In der Schule interessiert so gut wie ausschließlich der schließlich
erreichte stationäre Strom.]
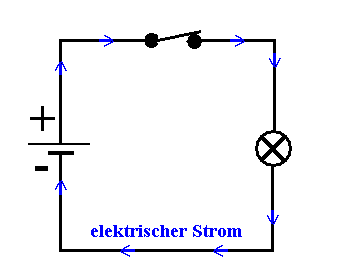 |
- Strom bedeutet "das Fließen" von Ladungen (nicht: "fließende
Ladungen"). Der elektrische Strom fließt definitionsgemäß
außerhalb der Stromquelle vom Plus- zum Minuspol, innerhalb
der Stromquelle dann weiter vom Minus- zum Pluspol, wieder aus
dem Pluspol heraus, immer ungeschwächt im
(unverzweigten) Kreis herum.
|
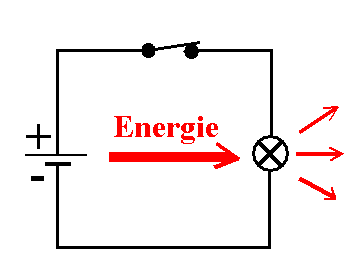 |
- Mit dem Strom ist ein gerichteter Energietransport von der
Stromquelle zum Widerstand ("Verbraucher") verbunden. Der
"Verbraucher" verbraucht keine Energie, aber er gibt Energie
nach außen hin ab bzw. wandelt sie in Energie einer anderen
Form um. Sie muss von der Stromquelle ersetzt werden.
[ Der Strom ist das Vehikel zum Energietransport. Aber die
Energie kann nicht in den bewegten Ladungen konzentriert sein,
da diese in der Beobachtungszeit in der Regel weder die
Energiequelle verlassen (sie können also in diesem Sinn - nach
Schülermeinung - keine Energie aufnehmen) noch den "Verbraucher"
erreichen (und dort diese Energie abgeben).]
| M.E. kann bereits der
einfache Stromkreis nicht verstanden werden, wenn
sich der Schüler nicht beider Transportvorgänge
bewusst ist! |
|
- Um eine Ladungsmenge Q durch einen Widerstand R im Stromkreis
hindurchzupumpen, muss die Arbeit W verrichtet werden. Diese ist
proportional zu Ladungsmenge Q. Die Proportionalitätskonstante definiert
die Spannung am Widerstand (den Spannungsabfall) U:
U = W/Q.
[ Die Definition dieses Spannungsabfalls entspricht der Definition einer
Spannung in anderen Fällen, nämlich als Potenzialdifferenz dort, wo
- anders als hier - ein Potenzialfeld und damit eine potenzielle
Energie von Ladungen tatsächlich vorliegen. Sie ist aber auch kompatibel
mit einer Ringspannung, wie sie z.B. wesentlich für die Induktion ist. W
ist dabei die Arbeit, die beim Transport der Ladung Q längs eines vollen
Umlaufs verrichtet wird.]
- Der Spannungsabfall ist ganz klar eine Folge des Stromflusses und
der Vorgänge in der Stromquelle. Unterbricht man nämlich den Strom
irgendwo im Stromkreis, dann verschwindet sofort der Spannungsabfall an
jedem Widerstand, genauso bei Abtrennen der Stromquelle.
- Die Stromarbeit, die beim Durchpumpen einer Ladung Q durch einen
Widerstand R mit dem Spannungsabfall U benötigt wird, wird von der
Stromquelle geliefert. Sie entspricht der Arbeit der chemischen "Kräfte"
in der Stromquelle. Sie ist nötig, weil die im Widerstand entstehende
Stromwärme ersetzt werden muss, soll nicht der Strom nach kurzer Zeit
zum Erliegen kommen.
[ Grund dafür sind - vereinfacht - Energieverluste der fließenden
Ladungen bei Stößen mit anderen Ladungen. Über Stromarbeit zu
reden ist ein didaktischer Trick, mit dem eine Diskussion des
Energiestroms weitgehend vermieden werden kann.]
- Lässt man den Gesamt-Widerstand gegen unendlich gehen, so geht die
Stromstärke gegen 0. Der dann zu messende Spannungsabfall am
Gesamt-Widerstand entspricht der Leerlaufspannung der Stromquelle.
Sie ist eine Eigenschaft der Stromquelle.
- In einem Wechselstromkreis verrichtet die Stromquelle bei beiden
Stromrichtungen Stromarbeit an den Widerständen des Stromkreises. Obwohl
der Strom seine Richtung ständig ändert, bleibt der Energiestrom zum
Verbraucher hin gerichtet.
[ Das elektrische Feld E und das magnetische Feld B
stellen sich jeweils so ein, dass dies möglich wird. ]
M.E. sollte an der Schule nicht behandelt werden:
- Wie die Energie von der Stromquelle zum Widerstand transportiert
wird.
- Welche Energieform dabei transportiert wird.
- Details der Vorgänge, wie sich der stationäre Strom einstellt.
Hinweise:
*) Bei der Induktion gibt es in der Regel keine
lokalisierte Stromquelle. Hier werden vorhandene Ladungen durch die
Ringspannung "im Kreis herum" gepumpt. Wie fließt
dann Energie in den ohmschen Widerstand des ringförmigen Leiters?
**) Bei idealen Bedingungen gilt: j = I/A = σ·E =
U/(l·ρ) mit dem spezifischen Widerstand ρ und der elektrischen
Leitfähigkeit σ , also I = U/R , weil σ = 1/ρ und E = U/l . In der
Übergangsphase vor Erreichen des stationären Stroms stellt sich die
endgültige Stromstärke einer bestimmten Größe ein, "der Widerstand begrenzt
den Strom". Von da an ist die Stromstärke im ganzen
unverzweigten Stromkreis konstant und überall gleich.
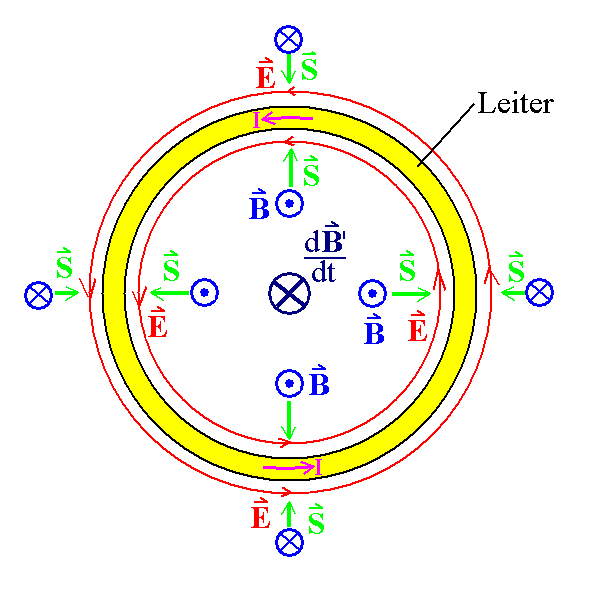 |
Nach Aussage des Poynting-Vektors (Energiestrom-Vektors)
S = 1/μ0 E x B
fließt die Energie aus der Umgebung in den Leiter hinein. Hier ist
E das elektrische Feld, das durch die Induktion im sich
ändernden Magnetfeld entsteht. B ist das Magnetfeld, das
der als Folge von E fließende Strom I um den Ringleiter
herum erzeugt. (So wird der Strom als Vehikel für den
Energietransport wirksam!)
Sollte als Folge der Induktion die Richtung von E
geändert werden (und damit auch die Stromrichtung), werden auch
die Richtungen von B geändert. Damit bleiben die
Richtungen des Energiestrom-Vektors S unverändert.
Es wäre absurd, hier anzunehmen, dass die
Leitungs-Elektronen "mit sich" von irgendwo her potenzielle
Energie herbeitragen, die in den Elektronen lokalisiert ist. Die
in den Feldern steckende Energie kommt vielmehr aus dem sich
ändernden B-Feld (B') bei der Induktion.
( Nach der Lenzschen Regel fließt der Induktionsstrom so, dass
er seiner Ursache entgegenwirkt, also B im Inneren des
Rings entgegengesetzt zu dB'/dt (∂B'/∂t), damit
der Veränderung von B' innerhalb des Rings
entgegengewirkt wird.)
M.E. sollte sich der Lehrer dieser Tatsachen bewusst sein,
sie im Unterricht aber nicht thematisieren.
|
Schülerversuche können zum Verständnis
beitragen.


