Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierigkeiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2018

Geschwindigkeit / Beschleunigung

.

Lernschwierigkeiten in der Mechanik können entstehen, wenn statt des "Orts-Konzepts" das überholte "Weg-Konzept" verwendet wird, wenn Geschwindigkeit mit "Tempo" verwechselt wird, wenn nicht zwischen laufender Zeit, Zeitpunkt und Zeitdauer bzw. Zeitintervall unterschieden wird, wenn nicht jeder Beschreibung einer Bewegung (i.d.R.) die Wahl eines Koordinatensystems vorausgeht. Es stimmt nur in 50% der Fälle, dass positive Beschleunigung ein Schnellerwerden bedeutet und negative Beschleunigung ein Langsamerwerden (Verzögerung). Lernschwierigkeiten müssen also entstehen, wenn negative Beschleunigung ausschließlich mit einem Langsamerwerden (Bremsen) in Beziehung gesetzt wird, und eine positive Beschleunigung ausschließlich mit einem Schnellerwerden.

.

Dabei ist klar, wie Geschwindigkeit und Beschleunigung "offiziell" definiert werden: Wenn r(t) bzgl. irgendeines willkürlich gewählten Koordinatenursprungs ein Ortsvektor ist, r(t+Δt) der Ortsvektor ein kleines Zeitintervall Δt später (oder früher) dann wird definiert:  v = lim Δr/Δt . Δt => 0 . wobei Δr = r(t+Δt) - r(t) die Änderung des Ortsvektors ("Vektor der Ortsänderung") im Zeitintervall Δt ist. Ganz entsprechend mit den Geschwindigkeitsvektoren v(t) und v(t+Δt):    a = lim Δv/Δt . Δt => 0 . wobei Δv = v(t+Δt) - v(t) die Änderung des Geschwindigkeitsvektors im Zeitintervall Δt ist. . .

.

Diese Definitionen sind für die Schule umzusetzen.

In manchen Schulbüchern zur 7./8. Klasse wird definiert: "Geschwindigkeit = zurückgelegter Weg/(dazu benötigte Zeit)", und dann später noch "genauer": "Unter der mittleren Geschwindigkeit (Durchschnittsgeschwindigkeit) einer Bewegung versteht man den Quotienten aus der Länge der gesamten zurückgelegten Wegstrecke und der dazu notwendigen Zeit". Im Band für die 11. Klasse der gleichen Reihe heißt es dann: "... der Gleiter ... legt in gleichen Zeitintervallen Δt gleiche Wegstrecken Δx zurück; er bewegt sich mit konstanter Geschwindigkeit v₀. v₀ = Δx/Δt = konstant - Definition der konstanten Geschwindigkeit".

Es ist klar: Nach dieser Definition kann eine Geschwindigkeit nie negativ werden, weil ja auch Weg oder Wegstrecke nie negativ sein können. Vielleicht war früher eine solche Definition sinnvoll, als man sich an Schulen auf geradlinige Bewegungen in eine einheitliche Richtung beschränkte. Seitdem man Schwingungen oder andere Hin-und Her-Bewegungen in den Schulunterricht hereingenommen hat, muss man die Richtungsinformation im Geschwindigkeitsbegriff berücksichtigen.

In der Didaktik unterscheidet man daher zwei Geschwindigkeitsbegriffe:

• Tempo (im Sinne der oben kritisierten Definition; es entspricht der Tachoanzeige eines Autos) und

• die eigentliche Geschwindigkeit gemäß der Definition des Kastens,

entsprechend der englischen Begriffe speed und velocity.

Überhaupt erscheint es wenig sinnvoll - außer wenn man nach den allereinfachsten Einführungen in der Schule schon wieder mit Bewegungen aufhört - die Kinematik auf die Zeitabhängigkeit von Wegen oder Strecken aufzubauen.

"Wir treffen uns nach 3 km Weg." Nicht einmal im eindimensionalen Fall kann jemand etwas mit dieser Information anfangen. Damit wäre verträglich a) vom Standpunkt aus 3 km nach Norden, oder b) vom Standpunkt aus 3 km nach Süden, oder c) 2 km nach Norden und dann 1 km nach Süden. Die Angabe "Wir treffen uns am Ort mit der Koordinate 3 km in Richtung Nord" wäre dagegen eindeutig.

Im Allgemeinen sollte man unterscheiden zwischen einem Zeit-Ort-Diagramm (auf dem man m.E. in der Schule seine Überlegungen aufbauen sollte) und einem Zeit-Weg-Diagramm (das man fast nie braucht). Statt dieses überholten "Weg-Konzepts" sollte man lieber das "Orts-Konzept" verwenden. Manche Autoren sprechen auch von Wegen, meinen aber - zumindest halbherzig - Orte.

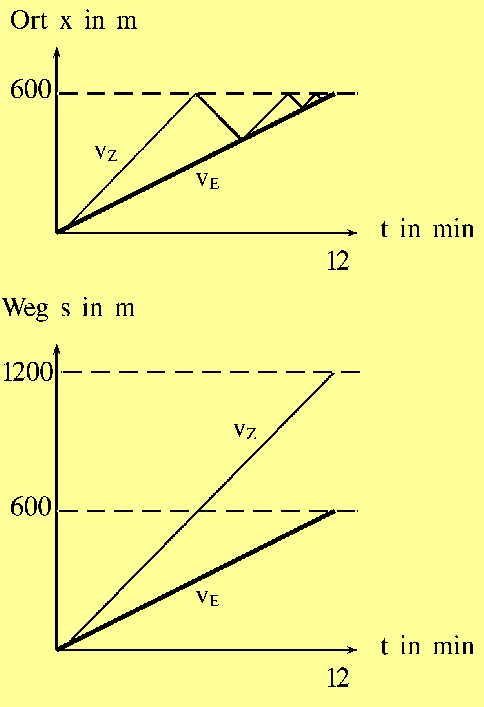
Ich habe den Unterschied immer erläutert an der bekannten Geschichte von Einstein und seinem Hund Zweistein, der zwischen dem großen Physiker und dem Patentamt - mit doppeltem Tempo(!) - immer hin und her pendelt. Die Frage ist, welchen Weg der Hund schließlich zurückgelegt hat. Ganz klar: gleiche Zeit, doppeltes Tempo => doppelter Weg (wenn man von den Zeitdauern der Richtungsumkehr des Hundes absieht). Beide befinden sich schließlich gemeinsam am Ort 600 m. Hier ist es sinnvoll, sowohl ein Zeit-Weg-Diagramm wie ein Zeit-Ort-Diagramm zu zeichnen:

Am Problem von Einstein mit seinem Hund Zweistein lässt sich der Unterschied zwischen einem t-x-Diagramm und einem t-s-Diagramm anschaulich begreifen.

Ausnahmsweise führt hier eine Überlegung am Zeit-Weg-Diagramm hinsichtlich der Fragestellung schneller zum Ziel. Sonst braucht man Zeit-Weg-Diagramme kaum.

(Die originale Anekdote habe ich vor vielen Jahren in einem Life-Time-Band ganz anders gelesen: Irgendjemand habe Physikern und Mathematikern diese Story vorgelegt. Typischerweise brauchten die Mathematiker immer viel länger zur Lösung, weil sie die einzelnen Wegstücke des Hundes aufsummierten. Nur John von Neumann, auch er Mathematiker, war noch schneller als typische Physiker. Gefragt, warum er als Mathematiker nicht auch die unendliche Summe gebildet habe, antwortete er angeblich: "Das habe ich doch gemacht!")

Unsinnigerweise behaupten einige Lehrbücher und Formelsammlungen sogar, dass der "Weg" auch im allgemeinen Fall ein Vektor sei. Obwohl das Wegelement Δs = v ·Δt seinen Vektorcharakter mit Recht vom Geschwindigkeitsvektor v erbt, ist nicht einmal klar, was die Richtung des "Weges" sein soll, es sei denn, man verwechselt den "Weg" mit dem Ortsvektor. Und eine Vektoraddition mit verschiedenen "Wegvektoren" macht wohl auch keinen Sinn.

Ein damit zusammenhängendes Problem ist das der Beschleunigung.

Zunächst gibt es schon mal ein Sprachproblem. Meine Schüler behaupteten von einem bewegten Körper immer, er "sei beschleunigt", was anfänglich meinen spontanen Protest herausforderte, bis ich mir bewusst machte, dass die Schüler vollkommen richtig geantwortet haben. Damit ein Körper in Bewegung kommen konnte, musste er erst beschleunigt werden. Die Schüler sagten ja auch nicht, wie wir, der Körper "beschleunigt" oder "wird beschleunigt", sondern sie sagen, er "ist beschleunigt".

Das didaktogene Problem entsteht aber

• erstens durch die Verwechslung von Tempo und Geschwindigkeit, die sich bei der Definition "Geschwindigkeitsänderung pro Zeiteinheit" auswirkt.
• Es entsteht zweitens durch die Behauptung, dass positive Beschleunigung mit einem Schnellerwerden verbunden sei, und eine negative Beschleunigung mit einem Langsamerwerden. Das ist leider nur in 50% der Fälle richtig. Denn, wenn die Geschwindigkeit negativ ist, z.B. wegen einer Rückwärtsbewegung, und es wirkt eine negative Beschleunigung, wird die Geschwindigkeit noch kleiner ("negativer"), also das Tempo größer.
• M.E. werden solche Lernschwierigkeiten selbst dann erzeugt, wenn der Schulbuchautor oder Lehrer für den einen Fall beiläufig sogar die richtige Bedingung angibt, nicht aber auf die zweiten 50% eingeht, wo also z.B. eine negative Beschleunigung mit einem Schnellerwerden verbunden ist (bei einer Rückwärtsbewegung). Die Kinematik einer harmonischen Schwingung lässt sich dann nicht verstehen.

Meines Erachtens gibt es folgende Auswege:

1. Schon von der ersten Einführung der Geschwindigkeit an wird diese den Schülern als Vektor nahegebracht, so dass die Richtungsinformation in den Schülerköpfen verfestigt wird: Vor Gebrauch einer Formel zeichnen die Schüler je nach der Bewegungsrichtung unterschiedliche Vektorpfeile, umso längere, je schneller der Körper ist. Beispiele zeigt das Bild (ähnliche Beispiele habe ich einmal in einen Artikel von Wiesner und Wodzinski gesehen).

Es sollen jeweils Geschwindigkeitspfeile eingezeichnet werden, die umso länger sind, je schneller der jeweilige Körper, hier bei Autos auf der Autobahn zur Zeit t = 0 s.	Hier zur Zeit 1 s später.
Hier fliegen Bienen zu einer Zuckerlösung, vielleicht umso schneller, je weiter sie noch entfernt sind.	Es ist gleichgültig, ob die Schüler davon ausgehen, dass der Betrag der Geschwindigkeit überall gleich ist oder nicht.

2. Bewegungen werden so gut wie ausschließlich dargestellt durch Veränderungen des Ortes (Ortsvektors) im Laufe der Zeit: "Orts-Konzept". Das setzt vor jeder Messung und jeder Rechenaufgabe voraus, dass sich die Beteiligten auf ein bestimmtes, wenn auch willkürliches Koordinatensystem einigen. Bei eindimensionalen Bewegungen ist dazu die Festlegung eines Koordinatenursprungs und einer positiven Koordinatenrichtung notwendig vor allen anderen Aktionen. Eine solche Strategie erleichtert das Aufgabenlösen an der Schule und evtl. später an der Hochschule. Dort ist die Wahl geeigneter Koordinaten vielfach schon der wichtigste Teil der Problemlösung. Das heißt aber auch, dass Bewegungen nicht sinnvoll beschrieben werden können, wenn die Schüler Koordinatensysteme noch nicht kennen.

3. Geschwindigkeit wird definiert als Ortsänderung pro Zeiteinheit, Beschleunigung als Geschwindigkeitsänderung pro Zeiteinheit. Das kann vektoriell wie auch koordinatenmäßig aufgefasst werden, nie aber betragsmäßig.

Besonders hilfreich ist es, dies an Graphen in Koordinatensystemen zu veranschaulichen - wieder muss man vorher Koordinatenursprung und positive Richtung (positiven Ort) festgelegt haben. In solchen Koordinatensystem erscheint die Geschwindigkeit als Steigung des t-x-Diagramms und die Beschleunigung als Steigung des t-v-Diagramms ("Denken in Graphen"). Von der zunächst anschaulichen Auffassung der Steigung aus (vgl. "manueller Steigungsbegriff") - sie erscheint mir physikalisch weitaus wichtiger als alle Grenzwertüberlegungen - ist dann nur noch ein kleiner physikalisch-begrifflicher Schritt zu Momentangeschwindigkeit und Momentanbeschleunigung. Beim häufig anzutreffenden Weg, der diese Begriffe formal mit Grenzübergängen aus dem Zeit-Weg-Diagramm in einer oder zwei Physikstunden herleitet, wozu sich der Mathematik-Unterricht Wochen an Zeit nimmt, bleibt m.E. bei den Schülern nur das Gefühl der Überforderung zurück. Und wenn es tatsächlich gelingen sollte, ihnen die zugehörige Mathematik nahezubringen, hätten sie doch für ihr physikalisches Verständnis zu wenig gewonnen.

Geht man aber so anschaulich vor, ist aus den Graphen unmittelbar ersichtlich, dass negative Beschleunigung manchmal mit einem Langsamerwerden zu tun hat, manchmal mit einem Schnellerwerden, aber immer mit einem Fallen im t-v-Diagramm. In Versuchen an der geneigten Fahrbahn lässt sich das eindringlich zeigen (Vgl. Buch Schülerversuche mit PC und ... ):

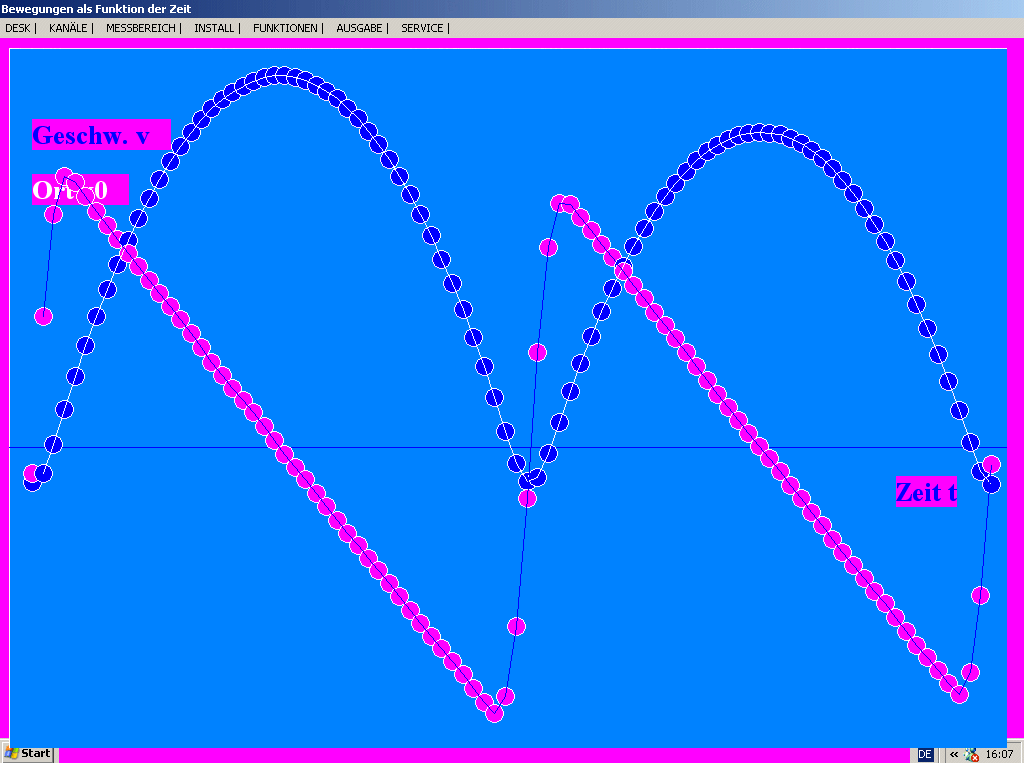Versuch an der geneigten Fahrbahn: Ein Gleiter wird nach oben geschossen, kehrt um und wird an Prallfedern wieder nach oben katapultiert. Das Sonarmeter (Programm SONAR: Bildschirmfoto) nimmt gleichzeitig das t-x- und das t-v-Diagramm auf. Wegen des fallenden t-v-Graphen muss die Beschleunigung negativ sein. Dazu gehören aber zwei Stellen mit größtem Tempo, nur eine davon auch mit größter Geschwindigkeit. Deutlich ist erkennbar, dass die Beschleunigung außer beim unteren Umkehrpunkt immer einheitliches Vorzeichen hat - wegen des gewählten Koordinatensystems immer negatives. Dennoch sind damit Phasen des Schneller- und des Langsamerwerdens verbunden. Der Koordinatenursprung ist hier in der Nähe des unteren Umkehrpunktes mit seiner Prallfeder gewählt worden, die positive Richtung ist die Aufwärtsrichtung. Hier bewährt sich das Sonarmeter besonders. Es ist ganz klar, dass auf dem Bildschirmfoto kein Weg-Zeit-Diagramm enthalten ist. Der Weg würde bei der Auf- und Abbewegung ständig zunehmen. Dagegen sind die Ortskoordinaten durch die Fahrbahn begrenzt.

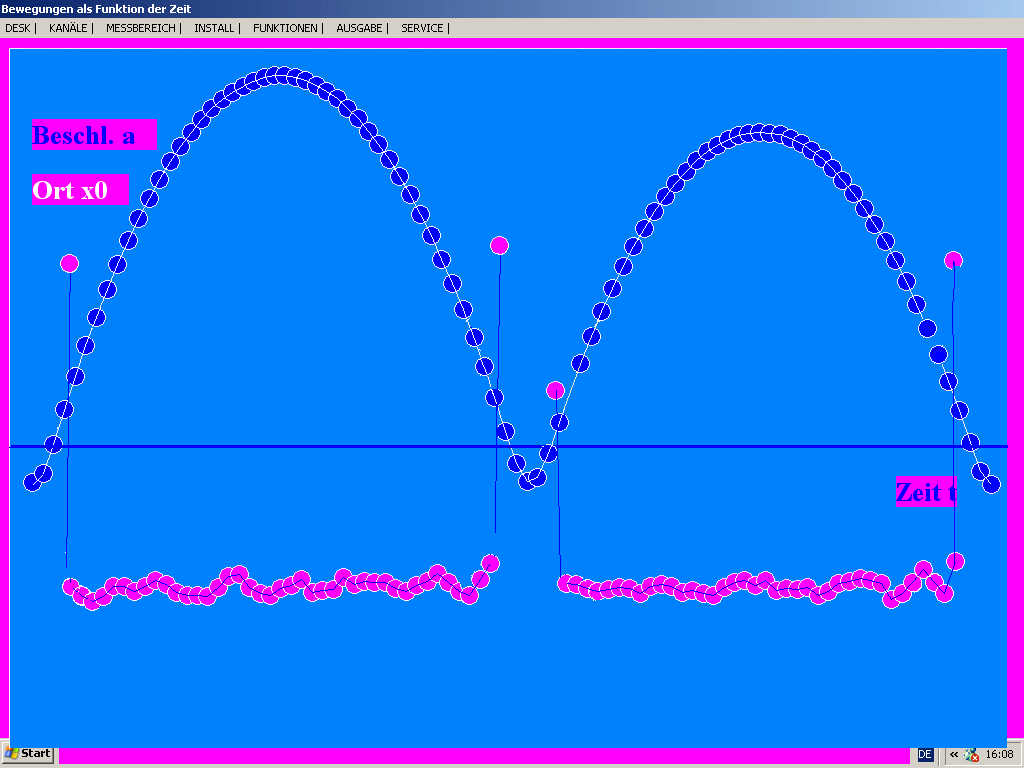Beim gleichen Versuch mit dem Sonarmeter (Programm SONAR: Bildschirmfoto) lässt sich auch das t-a-Diagramm mit ausgeben und bestätigt die Überlegungen am vorherigen Graphen. An den unteren Umkehrpunkten ist die Beschleunigung so groß (und positiv), dass die Messpunkte das Bildfeld verlassen. Eindrucksvoll wird bestätigt, dass selbst im oberen Umkehrpunkt, wo der Gleiter kurzzeitig ruht, die gleiche negative Beschleunigung herrscht. Ihre Folge sind sowohl ein Schneller- wie ein Langsamerwerden. Das Sonarmeter lässt sich nicht betrügen! Eine Verwechslung von Tempo und Geschwindigkeit ist nicht möglich!

.

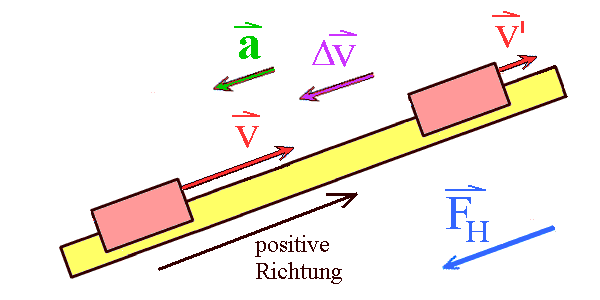Aufwärtsbewegung: Es ist sinnvoll, bereits an der 1-dimensionalen Bewegung Vektoren nicht formalisiert einzuführen und damit die Diagramme zu deuten: Der Kraftvektor F ist immer abwärts gerichtet (in negative Richtung, wenn der Ortsvektor x für die Aufwärtsbewegung in positive Richtung zeigt). Gleichgerichtet ist der Beschleunigungsvektor a (negative Beschleunigung), ganz gleich, in welche Richtung der Geschwindigkeitsvektor v zeigt: Kraft- und Beschleunigungsvektor sind sogar allgemein gleichgerichtet. Die positive Richtung ist so vereinbart, dass der Geschwindigkeitsvektor v bei der Aufwärtsbewegung in positive Richtung zeigt und bei der Abwärtsbewegung in negative Richtung.

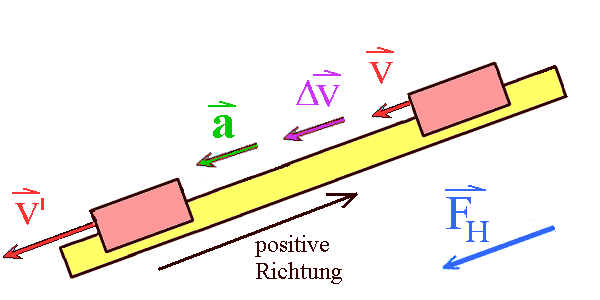Abwärtsbewegung: All dies lässt sich an den Sonarmeter-Diagrammen und den nebenstehenden Zeichnungen bestens erkennen. Negative Geschwindigkeit v heißt also: Der Geschwindigkeitsvektor v ist entgegengesetzt zur positiven Richtung orientiert. Siehe Geschwindigkeit als Vektor und auch Gleichmäßig beschleunigte Bewegung

Übrigens, manche Schulbuchautoren konstruieren hier eine weitere didaktogene Schwierigkeit: Manchmal reden sie dann doch von einem negativen Vorzeichen der Geschwindigkeit oder der Kraft und erläutern dieses dann, sicher nicht falsch, aber unvollständig, mit Vektoren und ihren Beträgen. Leider machen sie den Schülern nicht klar, dass es sich um Koordinaten bzgl. eines vorher (hoffentlich nicht nur implizit gewählten) Koordinatensystems handelt, deren Vorzeichen sich ganz automatisch ohne Willkür ergibt, wenn man anfangs ein Koordinatensystem festgelegt hat.

Die früher vielleicht sinnvolle Gewohnheit, Bewegungen durch die Zeitabhängigkeit von "Wegen" zu beschreiben, führt zu einem weiteren verwirrenden historischen Relikt. Weil zu Beginn einer Bewegung der zurückgelegte Weg per definitionem immer 0 sein muss, kennen viele Schulbücher nur eine einzige Anfangsbedingung, nämlich die Anfangsgeschwindigkeit. Die Newtonsche Bewegungsgleichung ist nun mal eine Differentialgleichung 2. Ordnung, die zwei Anfangsbedingungen zu ihrer eindeutigen Lösung erfordert (im eindimensionalen Fall). Irgendwann, wenn z.B. Schwingungen behandelt werden sollen oder die "Methode der kleinen Schritte", um mit nicht konstanten Kräften umgehen zu können, ist der "Anfangsort" als zweite Anfangsbedingung unvermeidbar. Dann wird häufig nachträglich - manchmal ohne ausreichenden Kommentar - die zusätzliche Anfangsbedingung hereingemogelt. Oder es führt zu unnötig aufwändigen Klimmzügen, wenn "gestückelte" Bewegungen betrachtet werden. Viel einfacher wäre es, wenn sich die Schüler recht schnell erarbeiten würden:

Die Schüler akzeptieren es ohne Weiteres, wenn man hinzufügt, dass man statt Δt auch t schreiben kann, wenn das Zeitintervall zur Zeit t = 0 beginnt. Die Beziehungen gelten, wenn das Zeitintervall Δt so klein ist, dass in ihm a in guter Näherung konstant ist. Diese Beziehungen sind in allen schulisch relevanten Fällen ausreichend, eventuell nur für kleine Intervalle Δt.

Überhaupt, das Symbol t, oft schlampig "Zeit" genannt! Ich habe es mir angewöhnt, sorgfältig (aber nicht pedantisch) zu unterscheiden:

• t könnte - ohne jeden Index - die laufende Zeit sein. Damit wird z.B. die Zeitachse eines Diagramms beschriftet oder es ist in einer allgemeinen Gesetzmäßigkeit enthalten und kennzeichnet dort eben die allgemeine Zeitabhängigkeit, etwa angezeigt durch eine laufende Uhr, die zu einem Zeitpunkt t = 0 eingeschaltet wurde. v(t) = v₀ + a·(t₁ - t) ist z.B. das Zeit-Geschwindigkeits-Gesetz, wenn zu einem Zeitpunkt t₁ eine Anfangsgeschwindigkeit v₀ vorlag, und wenn ab t₁ die Beschleunigung a konstant ist. Dann gilt die Gesetzmäßigkeit für beliebige laufende Zeiten t > t₁ . Der Koordinatenursprung bleibt dann bzgl. der Zeitachse unverändert, ganz gleich wie viele solche Intervalle aneinander gestückelt werden müssen.


• t könnte ein Zeitpunkt sein. Ich habe es mir angewöhnt, dann immer einen Index anzufügen. t_B ist dann z.B. der Zeitpunkt, zu dem ein Bremsvorgang beginnt, nicht die "Bremszeit".


• t könnte aber auch ein Zeitintervall oder eine Zeitdauer bedeuten. Dafür verwende ich nie ein einfaches t, sondern entweder Δt oder ich gebe die Länge des Intervalls durch Anfangszeitpunkt und Endzeitpunkt an. Die Länge eines Bremsvorgangs ("die Bremszeit") wäre dann z.B. Δt_B oder t_S - t_B , wenn t_S der Zeitpunkt des Stillstands ist und t_B der Zeitpunkt, zu dem der Bremsvorgang beginnt. Etwas inkonsequent schreibe ich auch manchmal t - t_B, wenn das Zeitintervall zwar zum Zeitpunkt t_B beginnt, aber durch die laufende Zeit begrenzt ist.

Besonders dann, wenn die Schüler eigene Ansätze zu Rechenaufgaben aufstellen sollen, bewährt es sich, wenn sie sich diese Unterscheidungen zu eigen gemacht hatten.