© Horst Hübel Würzburg
2005 - 2014
Spannungsdefinition "über potenzielle Energie der freibeweglichen Ladungen" ? Das Ein-Elektron-Potenzial-Modell |
I Zur Problematik einer Spannungsdefinition "über potenzielle Energie der freibeweglichen Ladungen"
|
I Zur Problematik einer Spannungsdefinition "über potenzielle Energie der freibeweglichen Ladungen"
Das ist eine von einem Lehrplanentwurf vorgeschlagene Formulierung, die recht problematisch erscheint.
1. Eine Spannungsdefinition als Potenzialdifferenz ist sicher dann möglich und üblich, wenn es ein Potenzial gibt. Das ist z.B. der Fall im geladenen Kondensator. Es ist z.B. nicht der Fall bei der Induktion. Innerhalb der Elektrostatik ist eine Definition der Spannung als Potentialdifferenz üblich und in jeder Hinsicht unangreifbar. Der Bereich der Elektrostatik wird aber bei stationären Strömen sicher überschritten. Aus Energieerhaltungsgründen kann es bei stationären Strömen kein Potential geben, wie in den meisten Elektrodynamik-Lehrbüchern nachzulesen ist. Hier sind stationäre Ströme nur möglich, wenn ein elektrisches Wirbelfeld (von einer "eingeprägten Feldstärke" oder EMK oder Umlaufspannung oder Ringspannung oder wie auch immer sie genannt wird) vorliegt. Eine potenzielle Energie für eine elektrische Ladung setzt ebenfalls ein elektrisches Potenzialfeld voraus: jedem Punkt des Raumes muss dann eindeutig eine potenzielle Energie bzw. ein Potenzial zugeordnet werden können. Das setzt Wegunabhängigkeit der Verschiebungsarbeit im elektrischen Feld voraus. Eine potenzielle Energie kann es immer nur von "etwas" (also z.B. einer Ladung oder einer Masse) an einem bestimmten Ort geben.
Die Ladung (oder Masse) hat dann an diesem bestimmten Ort eine bestimmte potenzielle Energie.
2. Die vorgeschlagene Formulierung suggeriert, dass es keine Spannung gebe, wenn keine freibeweglichen Ladungen vorliegen. Zwischen zwei Punkten im Dielektrikum eines geladenen Kondensators dürfte es demnach keine Spannung geben, weil es dort keine freibeweglichen Ladungen gibt. Zwischen zwei solchen Punkten besteht aber bekanntlich eine Potenzialdifferenz, also hier tatsächlich eine Spannung.
3. Es ist nicht klar, ob die Ladungen auf den Kondensatorplatten eines geladenen Kondensators als freibewegliche Ladungen im Sinne der Definition zählen. Einerseits handelt es sich ja bei den negativen Ladungen um die "freibeweglichen Leitungselektronen". Anderseits sind diese ja eben durch das Kondensatorfeld gebunden, also nicht frei beweglich. Zudem tragen nur die (relativ wenigen) Überschuss-Ladungen zum elektrischen Feld bei, die verschwindend wenige sind im Vergleich zu "den freibeweglichen Ladungen". Bekanntlich trägt bei einem guten Leiter jedes Atom ca. 1 freibewegliches Elektron zu den freibeweglichen Leitungselektronen bei. Dann sind in den Kondensatorplatten größenordnungsmäßig 1023 freibewegliche Elektronen vorhanden, bei C = 1 µF und U = 1 kV (also Q = 10-3 As) aber nur größenordnungsmäßig 1016 Überschussladungen, das sind 10-5 % der Leitungsselektronen.
4. Wenn man annimmt, dass die Kondensatorladungen als freibewegliche Ladungen zählen, dann sollte die Definition anwendbar sein. Man greife sich also irgendeine Ladung DQ auf den Kondensatorplatten heraus, dann ergibt sich gemäß U = DW/DQ die Spannung, aber nur, wenn DW die potenzielle Energie der Ladungsportion DQ auf dem Kondensator ist, sicher nicht der gesamten Ladung.
Wegen W = 1/2 Q · U für die im Kondensator gespeicherte Energie ergibt sich die richtige Spannung aus einer infinitesimal kleinen Ladungsportion DQ. ( W = 1/2 Q2/C => DW = 1/2 ·2 · Q/C · DQ = U · DQ durch Differentiation)
Man darf aber nicht annehmen, dass jede Ladung auf dem Kondensator die potenzielle Energie DW= DQ · U hat. Denn beim Aufbau der Ladung Q auf dem Kondensator musste immer mehr Arbeit verrichtet werden, je mehr Ladungen schon vorhanden waren. DW= DQ · U gilt nur für die bei der Spannung U zugeführte Ladungsportion DQ . Andernfalls würde man nicht zum Faktor 1/2 in W = 1/2 Q · U kommen: keine Arbeit für die erste Ladungsportion, maximale Arbeit DW= DQ · U für die letzte Ladungsportion; daraus ergibt sich der Mittelwert 1/2 DQ · U bzw. insgesamt 1/2 Q · U .
Die Annahme, dass alle ("die" laut dem erwähnten Lehrplanentwurf) freibeweglichen Ladungen die gleiche potenzielle Energie haben, führt also bereits beim einfachen Stromkreis mit einem Kondensator zum Widerspruch.
Grund für das Versagen der erwähnten Formulierung ist, dass nicht unterschieden wird zwischen den felderzeugenden Ladungen und einer beliebig kleinen Probeladung q (= DQ) im (evtl. Potential-)Feld der felderzeugenden Ladungen.
5. Trotz der erwähnten Formulierung: Alle freibeweglichen Elektronen in einem Stromkreis sollen wohl nicht dieselbe potenzielle Energie haben. Aber vielleicht alle in der Nähe des negativen Pols? Dann bräuchten wir nur den negativen Pol mit einem genügend großen Stück Kupfer verbinden und alle Energieprobleme der Welt wären gelöst: Nehmen wir an, dass bei einer 9 V Batterie mit U » 10 V alle freibeweglichen negativen Ladungen am negativen Pol gegenüber dem anderen die potenzielle Energie 10 eV hätten. Bei Cu beträgt die Dichte der freibeweglichen Ladungen n » 8.1028 m-3. Bei einer Elektrode von nur 1 m3 Volumen hätten die freibeweglichen Ladungsträger an der negativen Elektrode dann die gesamte potenzielle Energie von 10 eV. 8. 1028 = 5.1010 J » 14 MWh. Es ist leicht zu sehen, wie man diese Energie beliebig steigern könnte. Mit einer 1,5 V Monozelle könnte man das Energieproblem der Menschheit lösen! Wenn man nur genügend lange wartet, bis die Ladungen "alle" abgeflossen sind und ihre potenzielle Energie abgegeben haben, könnte man diese Energie dann als elektrische Energie nutzen. Bei einem Strom von 1 A werden pro Sekunde 1 C / 1,6·10-19 C » 6·1018 Elektronen durch einen Leiterquerschnitt transportiert, die nach dieser Rechnung 6·1018.10 eV = 6·1,6 J » 10 J pro Sekunde transportieren würden. Würde man das Kupferstück vom Minuspol abtrennen, würde es nach der falschen Überlegung des erwähnten Entwurfs noch 14 MWh / 10 J/s = 1,4 Mh dauern, bis alle freibeweglichen Ladungen des Kupferstücks ihre potentielle Energie bei 1 A verloren hätten. Schön wär's! Ganz klar, die Stromquelle denkt nicht daran, allen freibeweglichen Ladungen soviel Energie zuzuführen, sondern allenfalls den relativ wenigen, die den Strom transportieren! Das ist wie bei einem Speichersee: Auch wenn das Wasser im Speichersee insgesamt eine hohe potenzielle Energie hat, brauchen die Pumpen immer nur soviel Energie zu liefern, wie zum Ersatz der tagsüber entzogenen Energie nötig ist. Aber es ist nicht wie bei einem Speichersee, wo die im Wasser gespeicherte Energie abfließen würde, wenn man nicht mehr nachpumpen würde: Sobald man die Stromquelle abklemmt, kommt der elektrische Stromfluss in Sekundenbruchteilen zum Erliegen. An der Diskussion würde sich nur ein Faktor ändern, wenn man als "freibewegliche Leitungselektronen" nur die an der Fermikante auffassen würde.
Wieviel Energie aber transportieren die stromtransportierenden Leitungselektronen, wenn sie je 10 eV (Energie beliebiger Herkunft) mitbringen würden? In der Zeit Dt bewegen sich n.A.vD .Dt Ladungen durch den Leiterquerschnitt und geben Anlass zu einem Strom der Stromstärke I = e.n.A.vD . Es werden also n.A.vD Ladungen pro Zeiteinheit durch den Leiterquerschnitt transportiert. Dementsprechend beträgt die transportierte Leistung P = 10 eV n.A.vD = 10 eV / e . I , wenn jedes dieser Elektronen die Energie 10 eV mitbringt *). Bei I = 1 A ergibt sich P = 10 V .1 A = 10 W. Das wäre die Leistung, die an der Messstelle vorbeitransportiert wird. Sie würde dann in einen Widerstand hineintransportiert werden, wo jedes dieser Elektronen die Energie 10 eV abgibt. Die Größenordnung passt, aber eben nur, wenn die Stromquelle nur den stromtransportierenden Ladungen je 10 eV Energie mitgibt (also Arbeit verrichtet: über die Arbeit kann man problemlos Spannung definieren; das passt auch zu Leitfähigkeitsmodellen wie nach der Drude-Theorie). Das sind die Ladungen, die bei Stromfluss aus der Stromquelle herausgepumpt werden (und später wieder "eingesaugt" werden). Es bliebe immer noch die Frage, ob das potenzielle Energie ist, oder Feldenergie, wie die Elektrodynamik behauptet. Die müsste es ja eigentlich "wissen"! Sie sagt, dass das elektromagnetische Feld gerade die elektrische Arbeit verrichtet, die der Rechnung entspricht.
*) Das ist ja ganz korrekt: Die "wenigen" Ladungen, die in einer Zeiteinheit Dt den Strom durch einen Leiterquerschnitt transportieren, bewegen sich in einem elektrischen Feld, das durch die Batteriespannung U = 10 V aufgebaut wird. Sie verlieren bei einem vollen Umlauf jeweils die Energie 10 eV, bzw. verrichten die Arbeit 10 eV. In Schwierigkeiten käme man erst, wenn man "alle" freibeweglichen Ladungen abfließen ließe. Dann müsste man entweder annehmen, dass das Feld allmählich zusammenbricht (wie beim Kondensator), so dass die stromtransportierenden Ladungen immer weniger Energie mitbringen würde, oder dass die Stromquelle immer wieder freibewegliche Ladungen mit unveränderter Energie 10 eV nachliefert (wie beim stationären Strom). Es deutet sich auch in diesem Fall an, dass die transportierte Energie nicht Energie ist, die bestimmte Elektronen haben, sondern Energie, die von der Stromquelle geliefert wird (also Arbeit) mit den Elektronen als Vehikeln des Energietransports Vgl. Becker.
Solche Probleme würden nicht auftauchen, wenn man für den Fall, wo ein Potenzial vorliegt, also in der Elektrostatik, korrekt definiert hätte:
U ist der Quotient aus der potenziellen Energie einer Probeladung q im elektrischen Feld dividiert durch die Ladungsmenge q der Probeladung oder kurz: "potentielle Energie pro Probeladung".
6. Es gibt allerdings Fälle, wo kein Potenzial vorliegt, wie bei den Induktion. In diesem Fall kann es also auch keine Potenzialdifferenz geben, keine potenzielle Energie und damit auch keine Spannung im korrekt definierten Sinn einer Potenzialdifferenz der Elektrostatik. Bei der Induktion entsteht bekanntlich eine Ringspannung. Besteht man weiterhin auf der Spannung als Potenzialdifferenz, darf man nicht behaupten, dass bei der Induktion eine Spannung entstehe. Man könnte allerdings den Spannungsbegriff - unüblich - erweitern, wenn man auf die Wegunabhängigkeit (die dem Potenzialbegriff zugrunde liegt) verzichtet. Dann hat die potenzielle Energie einer Ladung keinen Sinn mehr.
Die offizielle Definition der Spannung nach DIN 1324
U = W / q ,
wobei W die Arbeit ist, die beim Transport der (Probe-)Ladung q verrichtet bzw. abgegeben wird) kann in diesem Fall aber weiter benutzt werden, wenn man auf die Wegunabhängigkeit der Spannung verzichtet.
 |
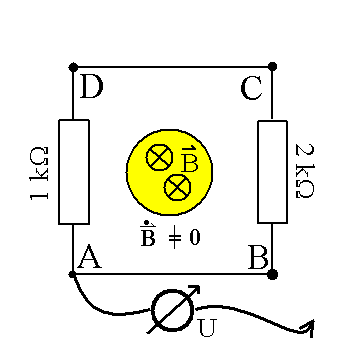
Bei einer Ringspannung von 5 V infolge der Induktion (dB/dt =/ 0) könnte die Spannung zwischen A und B 0 V, 5 V, 10 V oder 15 V sein: je nach Weg! |
(Bei der Induktion gilt ja bekanntlich rot E =/ 0, während bei einem Potenzialfeld rot E = 0 gilt). Verwendet man diesen verallgemeinerten Spannungsbegriff, können viele Aussagen tatsächlich so formuliert werden, wie es in der Schulphysik üblich ist. Nur dann kann man "von einer Induktionsspannung zwischen den Enden einer Induktionsspule" (die ja bekanntlich wegabhängig ist, und damit i.A. nicht den erwünschten Sinn hat; S. Abbildung) sprechen!
Durch eine solche minimale Korrektur könnte man viele der in der Schulphysik üblichen Falsch-Aussagen richtig stellen.
Schließlich hat es seinen guten Grund, weshalb man zwei Spannungsbegriffe hat:
7. Wenn man Spannung "über potenzielle Energie der freibeweglichen Ladungen" definieren möchte, müsste man noch klären, wie die Verhältnisse bei Wechselstrom sind, wo dann die "freibeweglichen Ladungen" in einer Periode zweimal ihre potentielle Energie ändern müssten. Wohin fließt dann diese potenzielle Energie. z.B. beim Wechsel von positiver zu negativer Polarität? In die Stromquelle zurück (bei einer "Reichweite" der Ladungen in atomarer Größenordnung?) ? ? Oder in den Widerstand ? ? Oder teilweise in den Widerstand und teilweise in die Stromquelle zurück ? ? Wie sollten sie ihre jeweils wechselnde "potenzielle Energie" erhalten?
Die wirklichen Verhältnisse, auch bei Wechselstrom, sind einfach: Die Elektronen sind nur Vehikel des Energietransports; sie ermöglichen die Ausbildung elektrischer und magnetischer Felder, die gerade so beschaffen sind, dass nach Aussage des Poynting-Vektors während jeder Halbperiode Energie (weitgehend in der Umgebung der Leiter) in den Widerstand fließt. Ob die Elektronen dabei eine bestimmte Energie haben oder nicht, ist dafür belanglos.
8. Die Elektrodynamik lehrt auch: Selbst, wenn man die wirklichen elektrischen Felder aufteilen kann (z.B. in Teilbereichen des Raums) in ein reines Wirbelfeld und ein reines wirbelfreies Feld (meinetwegen als Potenzialfeld bezeichnet), oder wenn dem reinen Wirbelfeld ein reines Potenzialfeld überlagert ist, so spielt dieses Potenzialfeld keinerlei Rolle beim Stromfluss: Stromfluss und Energielieferung sind allein eine Folge der "eingeprägten Feldstärke", also des Wirbelfelds, der EMK oder Umlaufspannung oder Ringspannung, also von Eigenschaften der Stromquelle.
Das ist auch ein Grund für das Versagen mancher Spannungsmodelle (Gravitations-, Höhen- , Höhendruck-Modell).
9. Im Vorangehenden hätte man statt Umwandlung von potenzieller Energie in kinetische oder Stromwärme immer sagen können, dass das elektrische Feld eine entsprechende Arbeit verrichtet. Hätten die Ladungen wirklich potenzielle Energie, müsste ein Potenzial vorliegen, das an die Wegunabhängigkeit der Verschiebungsarbeit gebunden ist. Dann müssten Ladungen auf jedem beliebigen Weg zwischen denselben Endpunkten dieselbe Energie verlieren oder gewinnen können. Sie denken nicht daran, dies auf dem Weg durch die Stromquelle zu tun! Um eine positive Probeladung außerhalb der Stromquelle vom Minus- zum Pluspol zu befördern, muss man positive Arbeit aufwenden; innerhalb der Stromquelle geht das "von allein".
II "Ein-Elektron-Potenzial-Modell"
1. In der Elektronik ist es üblich, Punkten innerhalb einer Schaltung ein "Potenzial" zuzuordnen, auch, wenn in der Schaltung stationäre Ströme fließen. Das hat sich offenbar bewährt. Auch, wenn p-n-Übergänge in Halbleitern beschrieben werden sollen, ist es üblich, einen "Potenzialverlauf" innerhalb der Grenzschicht zu zeichnen, und das hat sich offenbar auch bewährt bei der Erklärung von lokalen elektrischen Feldern, Raumladungsverteilungen und Energietransportvorgängen (Stromarbeit) innerhalb der Grenzschicht. So ist es sinnvoll, zu erklären, dass in der in Flussrichtung geschalteten Grenzschicht einer LED Leitungselektronen aus dem Leitungsband in Löcher des Valenzbands fallen (eher unter Beteiligung von zwischen beiden Bändern liegenden Akzeptor- bzw. Donatorzuständen), dabei ihre "potenzielle Energie" verlieren und diese in Form von Licht abgeben. Es gibt also offenbar ein erfolgreiches Erklärungs-Modell für solche Situationen, ich möchte es das "Ein-Elektron-Potenzial-Modell" nennen. Wie in Abschnitt 4 und 5 diskutiert, erhält man bei relativ wenigen Elektronen lokal an einem Widerstand oder einem p-n-Übergang die gleichen Energieumsätze, wenn man dieses Modell einsetzt oder die richtige Theorie mit der Arbeit des elektrischen Feldes. Das Modell ist für die Bewegung von einem Elektron im Feld der anderen und äußerer Quellen brauchbar. Man muss sich nur im Klaren sein, dass dieses Modell für relativ wenige Leitungselektronen funktioniert, im klaren Extremfall für ein einziges, maximal für soviele, dass durch sie das vorhandene elektrische Feld nicht verändert wird. Bei der Erweiterung zu sehr vielen Elektronen oder gar allen ("die") Leitungselektronen können quantitative Fehler entstehen oder gar die Sachverhalte völlig falsch dargestellt werden, wie oben diskutiert.
|
2. Nein, Spannung zwischen zwei Punkten ist ein Ausdruck des elektrischen Feldes zwischen den Punkten, vielleicht seiner möglichen Wirkungen ("potenziell", z.B. der Verschiebungsarbeit).
Vgl. auch: http://www.erz.uni-hannover.de/~physik/stroeme.html und auch Internet-Beitrag von Backhaus: Der Energietransport durch elektrische Ströme und elektromagnetische Felder in verschiedenen Darstellungen. Ein Beispiel für das Zusammenspiel zwischen Erfahrung und Konvention bei der physikalischen Begriffsbildung, Udo Backhaus, Fachbereich Physik der Universität Osnabrück