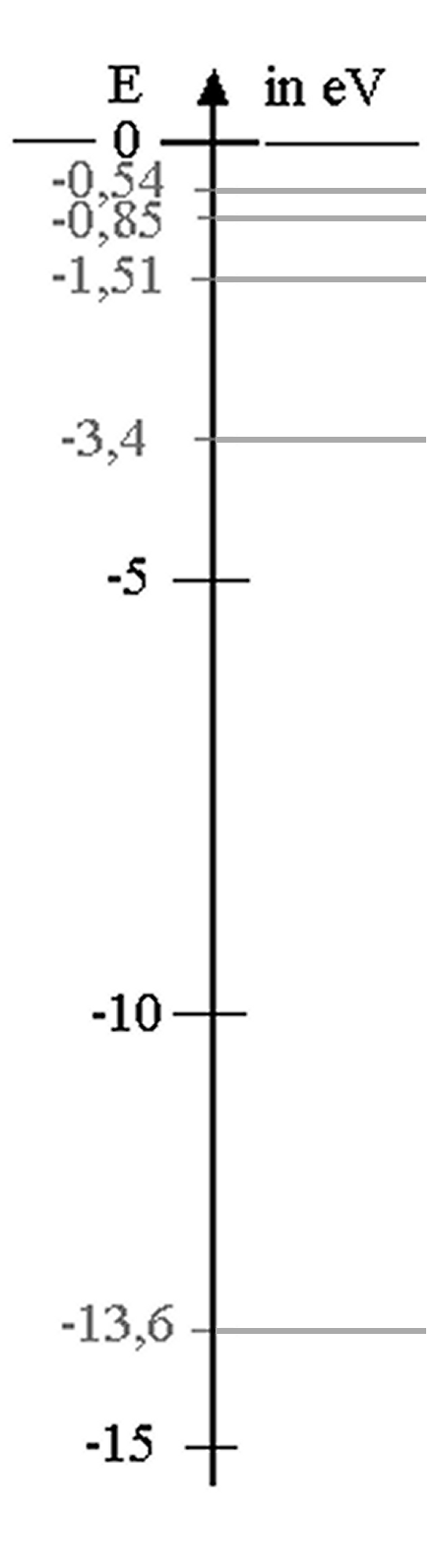Bohr'sches Atommodell - ein Revival ? Entwicklung einer Gesetzmäßigkeit am Beispiel der Balmer-Formel mit einer Tabellenkalkulation

1. Problematik:

In der Didaktik der Schulphysik ist das Bohr'sche Atommodell (BAM) aus verständlichen Gründen in Verruf geraten. Es widerspricht in zu vielen Punkten der etablierten Quantenphysik. Dazu gehören die Annahme von gleichzeitig be-stimmten Werten für Bahnradius r und Bahngeschwindigkeit v des angeblich kreisenden Elektrons oder von gleichzeitig be-stimmten Werten für kinetische und potenzielle Energie oder Gesamtenergie. Überflüssigerweise scheinen Schulbuchautoren gerade auf problematische Aspekte - Bahnkurve und Umlaufsgeschwindigkeit - besonderen Wert zu legen. Meines Erachtens zeigt aber das Bohr'sche Modell in einer für Schüler durchsichtigen Weise die Existenz diskreter Energiestufen im H-Atom und Folgerungen daraus für die Abgabe und Aufnahme von Energie durch das Atom. Man kann Balmers/Bohrs Überlegungen geradezu als die Entdeckung der Energiestufen des Atoms auffassen. Ich halte deshalb die Behandlung dieses Aspekts in der Schule für unverzichtbar. Hier möchte ich einen Weg aufweisen, wie die sicher falschen Aspekte des Bohr'schen Modells zurückgedrängt und die korrekten energetischen Aspekte in den Vordergrund geschoben werden können.

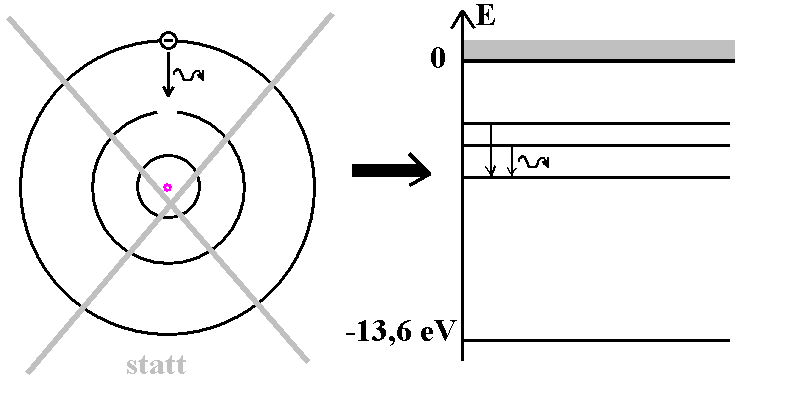
Abb. 1: Statt über Bahnen von Energiestufen sprechen!

2. Vom Spektrum zur Energieformel:

Das soll mit einem Tabellenkalkulationsprogramm geschehen, mit dem die beobachteten Photonenenergien der Balmer-Serie so analysiert werden,  dass die diskreten Energiestufen des H-Atoms erkennbar werden.

Im besten Fall eignet sich diese Untersuchung dann sogar als Schülerversuch, mit dem die Sch lernen, wie mit geeigneten Hypothesen eine mathematische Gesetzmäßigkeit "erraten" werden kann.

Im Buch

Schüleraktivierende Unterrichtsmaterialien, Band 3, Atomphysik, BoD, Norderstedt, 2009, ISBN 978-3-8370-1321-4 

sind Unterrichtsmaterialien bereit gestellt, die das folgende Programm in Aufgaben aufteilen, die von Schülern bewältigt werden können.

Die Spalten 3 und 4 der folgenden Tabelle enthalten die Eingangsdaten Photonenenergie E und Nummer n des Energieübergangs. Die übrigen Spalten ergeben sich um Laufe der Entwicklung.

E0	i = n + 2	E	n	E0 - E	n	1/(E0-E)	n	√[1/(E0-E)]
	1
	2
3,40	3	1,89	1	1,51	1	0,66	1	0,81
3,40	4	2,55	2	0,85	2	1,18	2	1,08
3,40	5	2,86	3	0,54	3	1,84	3	1,36
3,40	6	3,02	4	0,38	4	2,65	4	1,63
3,40	7	3,12	5	0,28	5	3,60	5	1,90
3,40	8	3,19	6	0,21	6	4,71	6	2,17
3,40	9	3,23	7	0,17	7	5,96	7	2,44
3,40	10	3,26	8	0,14	8	7,35	8	2,71
3,40	11	3,29	9	0,11	9	8,90	9	2,98
3,40	12	3,31	10	0,09	10	10,59	10	3,25

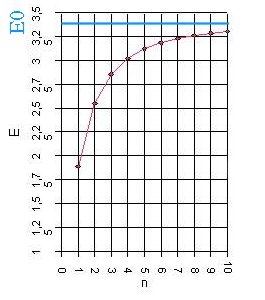Abb. 2: Zuerst wird die gemessene Photonenenergie E gegenüber einer Nummer n = 1,2,3, ... aufgetragen. Nach dem Graphen könnte man eine Asymptote vermuten, also einen Grenzwert E0 für die Energien; man vermutet E0 zwischen 3,3 eV und 3,5 eV. Wir wählen E0 = 3,4 eV.

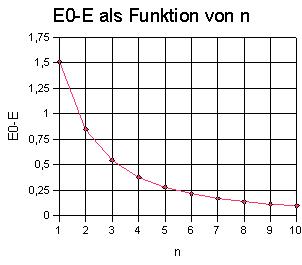Abb. 3: E0 - E als Funktion von n strebt gegen 0 für n gegen unendlich. Es könnte sich um eine Hyperbel handeln, versuchsweise wird 1/(E0-E) gegenüber n aufgetragen.

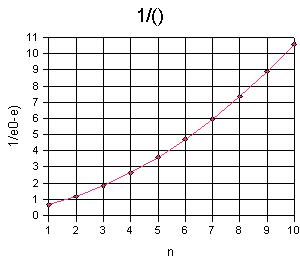Abb. 4: Der Graph ist immer noch stark gekrümmt. Es könnte sich um eine Parabel handeln mit dem Scheitel links von n = 1. Zieht man also die Wurzel, könnte sich eine Gerade ergeben.

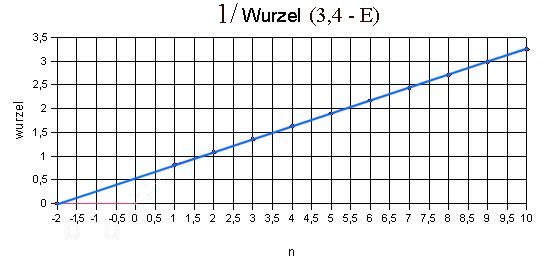Abb. 5: Das ist tatsächlich der Fall; man kann leicht entnehmen, dass der Scheitel bzw. der Nullpunkt der Geraden mit Steigung c bei n = -2 liegen. Daraus ergibt sich für das Quadrat ( E0 = 3,4 eV) 1/(E0-E) = c2 · (n+2)2 bzw. E = E0 - 1 / { c2 (n+2)2} .

Umbenennung (i = n+2) führt auf     E_i = E₀ - 1/ c² · 1/i².

c entnimmt man dem Graphen: Für n = 8, also i = n + 2 = 10 erhält man nach dem Graphen  1/√( - ) = 2,7.  c ist also 2,7/10 = 0,27.  1/c² ergibt 13,7. Anderseits ergibt sich für c = 0,271 der genauere Wert 1/c² = 13,6.

Durch Probieren erhält man die optimale Ausgleichsgerade für E₀ = 3,4 = 13,6 / 4, also   E_i = 13,6 · ( 1/4 -  1/i²) .

Damit lautet die Balmerformel endgültig (jetzt wieder mit Benennungen) für die Photonenenergie E_i  mit der Nummer i = 3, 4, 5, ... :

3. Die Entdeckung der Energiestufen im BAM:

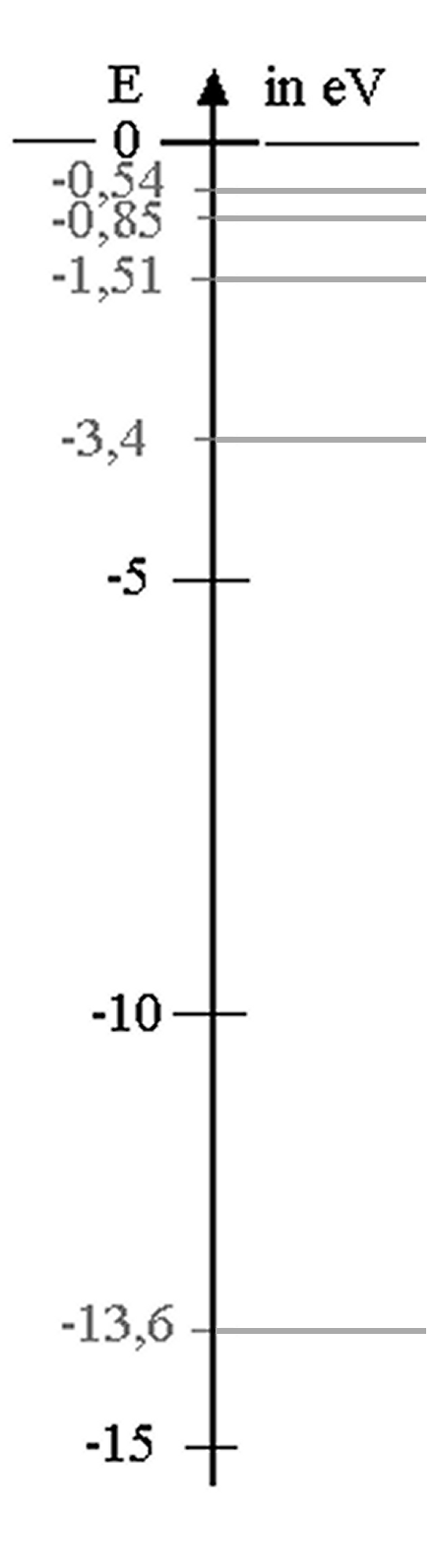Abb. 6: 1. Das ist die Entdeckung von Energieniveaus in Atomen! Für die n-te Energiestufe des Atoms wird der Ansatz gemacht:     En = - 13,6 eV /n2          ( n   = 1, 2, 3, ... ). 2. Daraus ergibt sich ein Energiestufenschema gemäß der Abbildung links. 3. Übergänge durch Strahlung: Die Photonenenergie Ei  entspricht der Differenz zwischen zwei Energiestufen:  Ei = En - E2 (n > 2). Bei der Balmer-Serie enden alle Übergänge auf der Energiestufe mit n = 2.

4. Das Bohr'sche Modell des H-Atoms a) Das Atom hat feste Energiestufen  En ; nur solche Energien sind erlaubt. b) Strahlung (Abgabe von Photonen) und Energieaufnahme (Aufnahme von Photonen) erfolgt nur durch Übergang von einer Energiestufe auf eine andere. Die Photonenenergie entspricht der Energiedifferenz. c) Das Elektron ist durch die Coulomb-Kraft an den Kern gebunden. d) Der Drehimpuls ist gequantelt, d.h. auch für ihn gibt es nur ganz bestimmte natürliche Zahlen n mit  m·v·2·r·π = n·h,  wobei n eine natürliche Zahl, oder auch: p·r  = n·ħ  wobei  ħ = h/(2·π)

.

5. Einige problematische Zusatzaspekte:

• Beim BAM wird fälschlich angenommen, dass ein Elektron auf einer festen Kreis-Bahn um den Kern läuft mit bestimmten Geschwindigkeiten. Diesen Aspekt würde ich nicht dadurch vertiefen, dass ich die Bahnkurve zeichne oder gar "Elektronensprünge" von Bahn zu Bahn visualisiere. Die Strahlung hat ja mit einer Ortsveränderung gar nichts zu tun.

• Beim BAM sollen Elektronen zugleich kinetische und potenzielle Energie haben und als Folge der Coulomb-Kraft soll auf der Kreisbahn gelten: E_kin = - 1/2 E_pot bzw. E_pot = - 2 E_kin   Daraus ergibt sich:      E = E_kin + E_pot = 1/2 E_pot =  - E_kin 

         Das folgt klassisch für eine Kreisbahn aus dem Coulomb-Gesetz.

6. Quantitative Charakteristika des Bohr'schen Atommodells:

(1) Für die Coulomb-Kraft gilt genauso wie für das Gravitationsgesetz:   Aus F = α /r²     folgt  E_pot = - α/r . Für das Coulomb-Gesetz gilt dabei α = 1/(4·π·ε₀ ) · Ze²  mit der elektrischen Feldkonstanten ε₀ = 8,85·10^-12 As/Vm  und der Kernladungszahl Z bei "wasserstoffähnlichen" Atomen. Das wird in Abschnitt 9 bewiesen.

(2)   E_kin = p²/2·m = m/2 v² = - 1/2 E_pot =  α/2r   ("Energiebedingung" als Folge des Coulomb-Gesetzes bei einer Kreisbahn mit Radius r) und damit:      E = E_kin + E_pot = 1/2 E_pot =  - E_kin. m = 9,1·10^-31 kg ist dabei die Masse des angeblich umlaufenden Elektrons.

(3)  m·v·2·r·π = n·h,  wobei n natürliche Zahl   ("Quantenbedingung")  bzw. p = n·h/(2·r·π) oder p·r=  n·ħ

( 𝓁 = p·r wird auch als Drehimpuls eines Teilchens mit dem Impuls p auf einer Kreisbahn mit dem Radius r bezeichnet. Die Quantenbedingung lautet dann 𝓁 = n·ħ mit ħ = h/(2·π))

7. Wie lässt sich die Herleitung von r und v vermeiden?

Einen möglichen direkten Weg zur Energie, der die Herleitung von r und v vermeidet, finden Sie unten.

8. Hinweise:

(1) Dass  E_pot =  -  α/r mit der Coulomb-Kraft zusammenhängt - klassisch argumentierend, wird durch Ableitung gezeigt: d E_pot / dr =   α/r² = - F_c  bei einer anziehenden Coulomb-Kraft zwischen zwei Ladungen Ze und -e.

(2) Dass E_kin = - 1/2 E_pot (1) beim Coulomb-Potential für eine Kreisbahn folgt - klassisch argumentierend - aus dem Kraftansatz: Die Coulomb-Kraft wirkt als Zentripetalkraft: mv²/r =  α/r² , also mv²/2 =  α/2r = - 1/2 E_pot. (Nur bei einer Kreisbahn ist  mv²/2 die gesamte kinetische Energie). Im allgemeinen Fall gilt eine entsprechende Beziehung nur für die Mittelwerte (Virialsatz).

(3) Mit der Beziehung (1) zu argumentieren und ihre Begründung nach Gebrauch nachzuschieben erscheint mir als sinnvoller Trick, aufwändige (und doch nur klassisch gültige) Rechnungen (für r und v) zu reduzieren. Primäres Ziel der Rechnung könnte dann sein, die Gesamtenergie  (basierend auf 13,6 eV) relativ schnell mit der Coulomb-Kraft und allgemeinen Konstanten zu begründen und nicht, Formeln für r oder v der "n-ten Quantenbahn" zu berechnen, obwohl der sogenannte klassische Atomradius r₀ = 0,5·10^-10 m für den Grundzustand für Vorstellung und Abschätzungen nicht uninteressant ist.

Der klassische Atomradius  r₀  ist aber eine reine Rechengröße. Er vermittelt ein Gefühl für die Größe eines Atoms. Tatsächlich würde man bei wiederholten Messungen das Elektron in jedem beliebigen Abstand vom Kern finden, am häufigsten allerdings in der Nähe des klassischen Atomradius, wie es auch das quantenmechanische Atommodell beschreibt.

(4) Hoch angeregte Rydberg-Atome (n > 60) verhalten sich in einem hohen Maß wie klassische Bohr'sche Atome. Beim Energie-Übergang von n auf n-1 stimmt sogar die Umlaufsfrequenz mit der Frequenz der abgestrahlten elektromagnetischen Welle recht gut überein. Dies sehe ich als ein weiteres Argument dafür an, dass das BAM in der Schule behandelt werden sollte.

(5) Beim H-Atom ist es gleichgültig, ob man von Energiestufen des Elektrons oder des Atoms spricht. Bei Mehrelektronenatomen hat streng genommen nur das Atom diskrete Energiestufen. Nur in vereinfachten Näherungs-Modellen, z.B. dem Schalenmodell, tut man so, als haben auch die Elektronen selbst be-stimmte Energiestufen.

(6) Wegen der gleichen Struktur von Coulomb-Kraft und Gravitationskraft (beide prop. 1/r²) gilt die Energiebedingung auch bei der Kreisbahn von Planeten. Das erlaubt einfache Abschätzungen für die Bewegung von Planeten um die Sonne oder von Satelliten um die Erde. Beim Gravitationsgesetz gilt α = G·m₁·m₂  mit G = 6,67·10^-11m³kg^-1s^-2  .

9. Anhang: Widersprüche des Bohr'schen Atommodells zur Realität und zum quantenmechanischen Atommodell:

(1) Es kann keine Bahnen von Elektronen im Atom geben; das widerspricht der Heisenberg'schen Unbestimmtheitsrelation (HUR).  Radius und Impuls/Geschwindigkeit können nicht gleichzeitig be-stimmt sein. Sie sind komplementär zueinander. Messungen des Orts oder der Geschwindigkeit (des Impulses) ergeben in den beschriebenen Zuständen streuende Messwerte: Das Elektron kann überall im Atom mit beliebiger Geschwindigkeit gefunden werden.

(2) E_kin oder E_pot können nicht gleichzeitig mit der Gesamtenergie E be-stimmt sein. Ebenso können auch E_kin und E_pot nicht gleichzeitig be-stimmt sein. Auch das wäre ein Widerspruch zur HUR. Je zwei dieser Größen sind komplementär. (Dagegen sollten auch schulische Herleitungen mit der Schrödinger-Gleichung nicht verstoßen.)

(3) Das H-Atom müsste flach wie eine Scheibe sein; tatsächlich "kugeliger Aufbau". Wir wissen: Ein Elektron in einem stationären Zustand mit einem be-stimmten Energieeigenwert "kreist" nicht. Es gibt im Atom keine Bewegung im klassischen Sinn. So gibt es keinen Grund, weshalb eine Kreisbahn die Geometrie des Atoms bestimmen sollte. Das Elektron kann bei Messungen überall im Atom gefunden werden.

(4) Energieänderungen sind nicht unbedingt mit Ortsveränderungen (Hüpfen von einer Bahn auf eine andere) verbunden. Weder vor, noch nach der Energieänderung hat ja nach der Quantentheorie das Elektron ohne eine Messung einen Ort. "Quantensprünge" in diesem Sinne gibt es also nicht.

(5) Die magnetischen Eigenschaften des H-Atoms kommen falsch heraus. Das klassisch im H-Atom kreisende Elektron müsste wie ein Kreisstrom ein Magnetfeld erzeugen. Das ist für den Grundzustand nicht der Fall, wie schon die erweiterte Bohr-Sommerfeld-Theorie zeigte. Dann wäre das H-Atom also nicht paramagnetisch. Das widerspricht aber den Experimenten, weil auch der Elektronenspin eine Rolle spielt. Allein wegen des Elektronenspins ist das H-Atom im Grundzustand paramagnetisch.

(Bei der überholten Bohr-Sommerfeld-Theorie sind zusätzlich zu den Kreisbahnen auch Ellipsen zugelassen. Bahnen mit gleicher großer Halbachse gehören zur gleichen Hauptquantenzahl n (zur gleichen Energie). Die verschiedenen Ellipsenformen werden durch die Bahndrehimpulsquantenzahl 𝓁 unterschieden.)

(6) Es wird nicht erklärt, weshalb das kreisende Elektron nicht wie ein Dipol elektromagnetische Wellen abstrahlt. Dann müsste es nämlich wegen des Energieverlusts in den Kern "spiralen" und das Atom instabil machen. Wir wissen: Ein Elektron in einem stationären quantenmechanischen Zustand mit einem be-stimmten Energieeigenwert "kreist" nicht, weil es nicht eine Folge von Orten durchläuft. So gibt es keinen Grund, weshalb es strahlen sollte.

(7) Damit hängt zusammen: Die Umlaufsfrequenz müsste sich beim BAM im Laufe eines Strahlungsvorgangs verändern. Dabei sollte sich auch die Frequenz des abgestrahlten Lichts verändern. (Ein schwingender Dipol strahlt eine elektromagnetische Welle gleicher Frequenz ab): Ein H-Atom-Gas sollte nicht die Balmer-Serie abstrahlen, sondern weißes Licht mit Photonen aller Energien.

(8) Es wird nicht erklärt, weshalb der Drehimpuls gequantelt sein soll. Tatsächlich zeigt die Quantentheorie des H-Atoms (wie auch schon die Bohr-Sommerfeld-Theorie), dass es zur Hauptquantenzahl n mehrere Drehimpulsquantenzahlen 𝓁 (für den Bahndrehimpuls) geben kann: 𝓁 = 0, 1, ... n-1. Für den Grundzustand mit n = 1 ist also nur eine einzige Drehimpulsquantenzahl (𝓁 = 0) möglich. (Deshalb also gibt es im Grundzustand keinen "Bahnmagnetismus", sondern nur den "Spinmagnetismus").

(9) Weitere Details der Strahlung (z.B. die so genannte Feinstruktur) lassen sich so nicht erklären. Generell wird der Elektronenspin wie der Kernspin außer acht gelassen.

(10) Es sind keine Aussagen über die Intensität der Spektrallinien möglich.

(11) Das Bohr'sche Atommodell lässt sich kaum auf Atome mit mehr als einem Elektron erweitern.

(12) Die Quantenphysik lehrt, dass es - streng genommen - in einem Mehrelektronen-Atom ohne Messung auch keine individuellen Elektronen gibt. Bereits beim He-Atom gibt es ohne eine Messung keine zwei individuellen Elektronen mit be-stimmten Eigenschaften. Wir wissen: Die Wellenfunktion der Schrödinger-Gleichung ist in diesem Fall eine Welle in einem 6-dimensionalen Raum. Erst durch eine Messung entstehen individuelle Eigenschaften von Elektronen. (Mit Näherungsmethoden setzt man sich manchmal über diese Tatsache hinweg.)

10.  Anhang: Herleitung der Energiezustände des BAM:

Ausgangspunkt sind: 

( 𝓁 = p·r = n·ħ p·r = n·ħ wird auch als Drehimpuls eines Teilchens mit dem Impuls p auf einer Kreisbahn mit dem Radius r bezeichnet. )

E_kin ist prop. zu p², E_pot prop. 1/r. Um p·r ins Spiel zu bringen, ist die Kombination E_kin/E²_pot oder ihr Kehrwert geeignet.

Sie erhalten: E_kin/E²pot = p²/2·m /(α/r)² = p²r²/(2mα²) = n²·ħ²/(2mα²)               

Wegen der Energiebedingung gilt E_kin/E²_pot = 1/(4·E_kin), und schließlich:

E_kin =  (mα²/2)·1/(n²·ħ²)  n ε N,       

insgesamt also für die Gesamtenergie im n-ten Zustand:

E_n = - E_kin = - (m·α²/2) 1/(n²·ħ²)  n ε N                oder mit α = 1/(4·π·ε₀ ) · Ze² und  ħ = h/(2·π)

E_n =  - (Z²·m·e⁴)/(8·ε₀²·h²)·1/n²    bzw.  

  mit der Grundzustandsenergie E₁ = - (Z²·m·e⁴)/(8·ε₀²·h²) ,    wobei n ε N.

Auf diese Weise können Sie ohne Herleitung von r und v die Energiestufen E_n des Wasserstoffatoms erhalten. In der Diskussion dieses Ergebnisses wird das Energieniveau-Schema von Abb. 6 bestätigt.

*) Mit der nicht duden-gemäßen Schreibweise von "be-stimmt" wird angedeutet, dass es sich um das quantenphysikalische Fachwort und nicht um das gleichlautende umgangssprachliche Wort handelt.

Download:   balmer_leer.xls       balmer_leer.ods

( März 2016 :  Zeichensatz geändert; 2024: überarbeitet )