Kreisbewegung eines Massenpunktes

Auch hier erscheint es sinnvoll, die Dynamik der Bewegung zu betonen und kinematische Begriffe erst dann einzuführen, wenn sie für die Dynamik erforderlich sind. Zwei der notwendigen Begriffe sind Winkelgeschwindigkeit und Bahngeschwindigkeit. Ein Experiment zeigt, dass bei der Kreisbewegung zwei Geschwindigkeitsbegriffe notwendig sind. Versuch: Ein Spielzeug-Auto ("Darda-Auto") durchläuft nach 2 m Anlauf zwei Loopings unterschiedlichen Durchmessers. Obwohl die Schüler annehmen können, dass beide grob mit derselben Bahngeschwindigkeit durchlaufen werden, entsteht beim kleineren der Eindruck einer größeren "Schnelligkeit", weil die Umlaufszeit geringer ist. 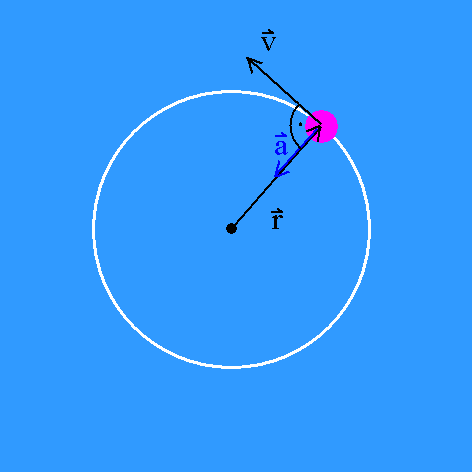Das motiviert zur Definition von Bahngeschwindigkeit und Winkelgeschwindigkeit.

Ein wichtiger Gesichtspunkt ist auch hier, dass Kraft und Beschleunigung gleichgerichtete Vektoren sind. Dass eine Kraft  F nötig ist, folgt aus der Tatsache, dass die Geschwindigkeit (d.h. der Geschwindigkeitsvektor v) nicht konstant ist. Es muss eine Kraft geben, die die ständigen Richtungsänderungen bewirkt, die Zentripetalkraft (im Falle einer gleichförmigen Kreisbewegung). Die Bewegung heißt gleichförmig, wenn die Winkelgeschwindigkeit konstant ist, bzw.  wenn bei konstantem Radius der Betrag der Geschwindigkeit konstant ist. Eine gleichförmige Kreisbewegung ist keine gleichförmige Bewegung!

Man sollte mit Überlegungen zu den beteiligten Vektoren anfangen, mit Vektoren ohne Koordinatendarstellung, damit ihre physikalische Funktion von vornherein klar ist, also mit Überlegungen zu  den Vektoren r, v, a und, gleichgerichtet, F. Wenn die physikalischen Sachverhalte verstanden sind, kann auch die Mathematik der Koordinatendarstellung nachgeschoben werden. Aus ihr kann im Wesentlichen folgen, dass bei der gleichförmigen Kreisbewegung Kraft und Radiusvektor entgegengesetzt gerichtet sind, und dass die Winkelgeschwindigkeit in einer bestimmten Weise mit der Bahngeschwindigkeit und dem Radius r zusammenhängt. Diese Aussagen kann man aber auch experimentell oder anders erarbeiten.

Vektoren bei der gleichförmigen Kreisbewegung: r Ortsvektor (x), vom Koordinatenursprung, der in der Regel mit dem Kreiszentrum zusammenfallend gewählt wird, zur momentanen Position des rotierenden Punktes, manchmal auch "Fahrstrahl" genannt v Geschwindigkeitsvektor parallel zur momentanen Bewegungsrichtung, bei der Kreisbewegung also senkrecht zum Ortsvektor, a Beschleunigungsvektor als Folge der ständigen Geschwindigkeitsänderungen (Richtungsänderungen), senkrecht zu v F Vektor der Kraft, die diese Geschwindigkeitsänderungen (Beschleunigungen) bewirkt. Sie ist gleichgerichtet mit dem Beschleunigungsvektor a (links handelt sich um eine Zeichnung)

Die Überlegungen können bestätigt werden durch ein Experiment mit zwei Sonarmetern, die eine Kreisbewegung vollständig registrieren können. Die beiden Sonarmeter "schauen" unter 900 auf einen Stab, der um die Achse eines Experimentiermotors (mit Bohrfutter) rotiert und dabei parallel zur Achse steht. Ein Stab wird verwendet, damit das Sonarmeter, gerichtet gegen die Spitze des Stabs,  trotz seiner Winkeldivergenz nicht etwa das Bohrfutter sieht. Mit dem Programm SONAR lässt sich eine "Radar-Darstellung" des rotierenden Stabes auf den Bildschirm bringen.  (Vgl.  Buch zu Schülerversuchen, obwohl dieser Versuch gerade nicht so als Schülerversuch geeignet ist). Das Programm nimmt eine notwendige Korrektur des Parallaxenfehlers vor, wenn der Radius eingegeben wird. Die folgenden Bildschirmfotos ergaben sich aus dem Unterricht  am Friedrich-Koenig-Gymnasium Würzburg (FKG).

Bildschirm-Aufnahme einer realen Drehbewegung mit 2 senkrecht zueinander orientierten Sonarmetern mit dem PC-Programm SONAR: Aus den jeweiligen Orts-Koordinaten wird der Orts-Vektor berechnet und vom Programm eingezeichnet. Im Laufe der Drehbewegung verändert sich der Vektor quasi wie in einem Video. Leichte Abweichungen der Bahn von der Kreisform sind hier durch Fehler der zueinander senkrechten Orientierung der Sonarmeter und der Tatsache bedingt, dass als rotierender Körper eine Stange mit 8 mm Durchmesser (bei 5 cm Bahnradius) verwendet wurde. Die Messung des Kreiszentrums, die das Programm vornimmt, ist also in beide Richtungen mit geringen Fehlern behaftet, die sich auch  geringfügig in der parallaktischen Korrektur auswirken.

Bildschirm-Aufnahme einer realen Drehbewegung mit 2 senkrecht zueinander orientierten Sonarmetern mit dem PC-Programm SONAR: Die Geschwindigkeitskoordinaten werden mitgemessen und der Geschwindigkeits-Vektor eingezeichnet. Im Laufe der Drehbewegung verändert sich der Vektor quasi wie in einem Video.

Bildschirm-Aufnahme einer realen Drehbewegung mit 2 senkrecht zueinander orientierten Sonarmetern mit dem PC-Programm SONAR: Für jede Koordinate wird die Beschleunigung mitgemessen und als Vektor eingezeichnet. Im Laufe der Drehbewegung verändert sich der Vektor quasi wie in einem Video. Man kann in gewissen Grenzen zeigen, wie sich die Vektoren verändern, wenn die Umlaufszeit oder Bahngeschwindigkeit verändert wird. Insbesondere die Veränderung des Beschleunigungsvektors bei sich ändernder Winkelgeschwindigkeit oder Bahngeschwindigkeit ist eindrucksvoll. (Dass hier der Beschleunigungspfeil quasi am Zentrum endet, ist Zufall, der sich durch Ändern der Winkelgeschwindigkeit leicht vermeiden lässt. Es kann sicher die qualitative Aussage hergeleitet werden: Mit zunehmender Bahn-/Winkelgeschwindigkeit wächst die notwendige Zentralbeschleunigung bzw. Zentralkraft.