Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig- keiten im Physik-UR An- schauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Kausalität

Kausalität bedeutet in der Mechanik:

Das ist also das Programm der Newtonschen Mechanik und die eigentliche Aussage im 2. NG. Aus ihr ergibt sich die Möglichkeit "die Zukunft vorherzusagen", wenigstens dort, wo Kausalität anwendbar ist.

Der Kausalitätsbegriff ist nicht in allen Fällen anwendbar. Einschränkungen gibt es in der Quantenphysik, bei makroskopischen Systemen aus sehr vielen Teilchen und bei komplexeren, speziell nichtlinearen Systemen sogar in der klassischen Mechanik (vgl. "Chaostheorie").

Für konstante Kraft auf ein klassisches Teilchen bzw. eine gleichmäßig beschleunigte Bewegung wird also  Kausalität beschrieben durch das folgende Kausalkettenschema:

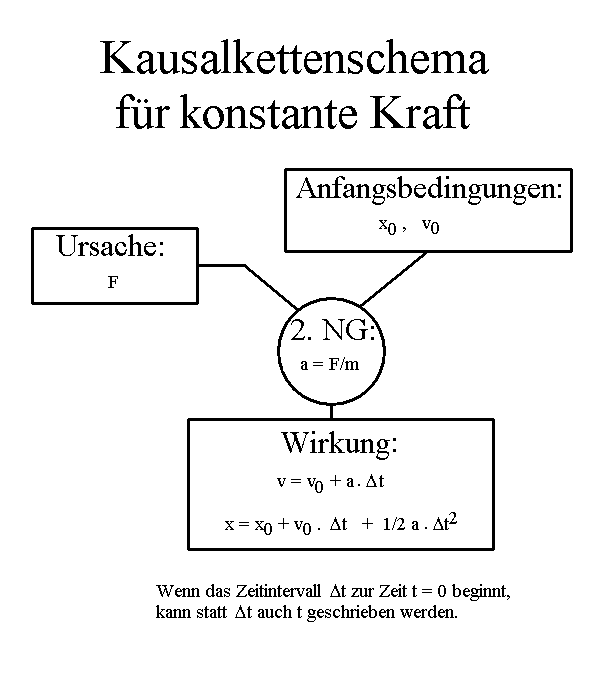Bei zeitlich veränderlicher Kraft muss man sich auf kleine Intervalle Δt beschränken, in denen F bzw. a in guter Näherung konstant sind. An ein solches Intervall muss sich dann das nächste anschließen mit Anfangsbedingungen, die sich aus den momentan erreichten Werten für x und v ergeben. Die geänderten Werte x₀ und v₀ bestimmen evtl. eine geänderte Kraft F, die wiederum zu einer geänderten Beschleunigung a führt u.s.w. Das ist die "Methode der kleinen Schritte".

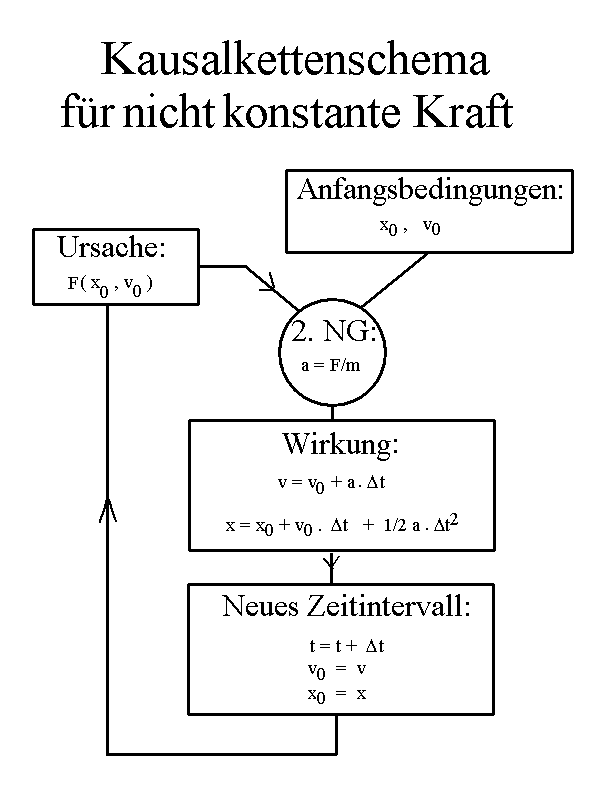Die "Methode der kleinen Schritte (MdkS)" bewährt sich in der Schule erstmals für einen Fall mit Luftreibung bzw. für eine harmonische Schwingung.

Es wird häufig vorgeschlagen, den quadratischen Term wegzulassen, weil er für sehr kleine Zeiten klein gegenüber dem linearen Term sei, wie man sich auch überzeugen kann. Für die Mitnahme des quadratischen Terms sprechen andererseits folgende Argumente:

• Bislang, bei konstanter Kraft, haben sich die Schüler mühsam daran gewöhnen müssen, dass ein solcher quadratischer Term notwendig ist. Es wäre aus didaktischen (nicht praktischen) Gründen inkonsequent, ihn jetzt auf einmal wegzulassen.

• Im Prinzip könnte man sich auch für eine konstante Kraft mit Hilfe der "Methode der kleinen Schritte" von Intervall zu Intervall durcharbeiten. Obwohl das Problem sehr einfach exakt lösbar ist, müsste man zu sehr kleinen Zeitintervallen Δt übergehen um mit der MdkS ohne quadratischem Term ein halbwegs genaues Ergebnis zu erhalten. Mitnahme des quadratischen Terms führt jedoch für beliebige Zeitintervalle zum exakten Ergebnis.

• Der quadratische Term bedingt eine "Konvergenzbeschleunigung", die dafür sorgt, dass z.B. bei der harmonischen Schwingung schon bei recht großem Zeitintervall (im Vergleich zur Schwingungsdauer) ein halbwegs oszillierendes Verhalten herauskommt. Mitnahme des quadratischen Terms liefert Ergebnisse, die mit der aufwändigeren "Halbschritt-Methode" vergleichbar sind.

• Dem PC ist es gleichgültig, ob er bei der Berechnung auch noch den quadratischen Term mitnimmt oder nicht. Eine Rechnung mit dem Taschenrechner (oder gar im Kopf) wird man ohnehin höchstens einmal durchführen, für eine Zeit, zu der der quadratische Term noch leicht zu berechnen ist. Den Rest wird man immer dem PC überlassen.

  Ein Ergebnis für ein Kraftgesetz nach Hooke:   F = - D·x zeigt das folgende Bildschirmfoto vom PC-Programm KAUSALIT:

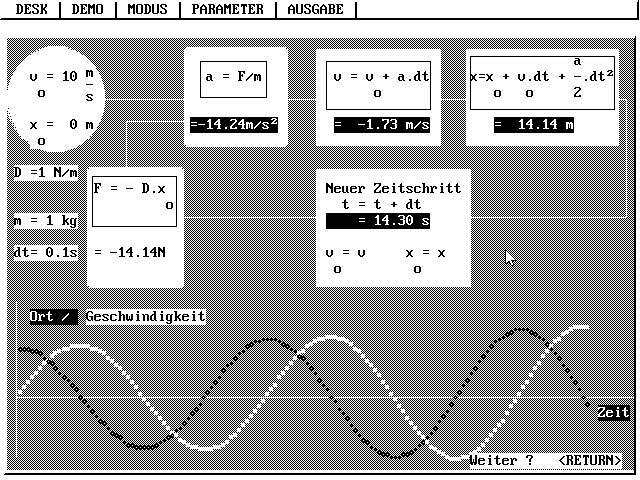
  Nachdem die Schüler 2 (max. 3) Zeitschritte des Kausalitätsschemas für eine harmonische Schwingung im Kopf oder mit dem Taschenrechner durchgerechnet haben, übernimmt das Programm KAUSALIT (hier in einer älteren Version) die Rechenschritte. Nach jedem Tastendruck wird ein weiterer Zeitschritt eingetragen mit den zugehörigen Punkten in ihren Graphen. Man sieht, dass die Amplitude mit zunehmender Zeit zwar leicht größer wird, aber doch weniger als ohne den quadratischen Term.

  Das Kausalitätsprogramm kann auch für mehrdimensionale Bewegungen wie Wurf und Planetenbewegung angewandt werden. Bei der Planetenbewegung sind allerdings kartesische Koordinaten recht ungünstig.

  .

  .