Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierigkeiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Impuls-Erhaltungssatz vor Energie-Erhaltungssatz

Diese Reihenfolge scheint besonders günstig zu sein, weil bei Stoß-Experimenten das Phänomen der Impuls-Erhaltung in einer Eindringlichkeit herauskommt, die beim Energie-Erhaltungssatz nur schwer zu erreichen ist. Es wird auch klar, dass der Grund für die Definition eines neuen Begriffs, des Impulses p, eben genau der ist, dass er bei Stößen erhalten bleibt.

Nachdem geklärt ist, dass jetzt eine neue Art von Mechanik beginnen soll, die anders als die Newtonsche Mechanik auf den Kraftbegriff verzichtet (der Name "Mechanik der Erhaltungssätze" wird noch nicht verraten), werden Stoßexperimente an der Fahrbahn durchgeführt.

• Ein Gleiter stößt elastisch gegen einen ruhenden gleicher Masse. Die Schüler beobachten, wie der stoßende Gleiter fast schlagartig stehen bleibt und der zweite Gleiter davon gestoßen wird. Es sieht so aus, als habe er die frühere Geschwindigkeit übernommen.

• Vielleicht fordern die Schüler ein verbessertes Experiment, bei dem die Geschwindigkeit vor wie nach dem Stoß gemessen wird. Der Lehrer schlägt eine Messung mit zwei Lichtschranken vor. Das Ergebnis zeigt die nächste Abbildung.

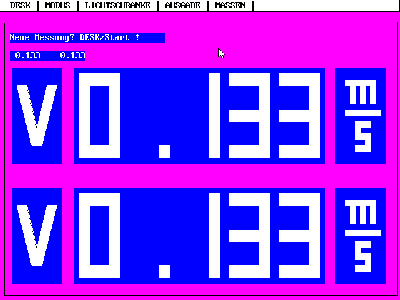  Elastischer Stoß eines Gleiters mit einem ruhenden gleicher Masse, gemessen mit Lichtschranken. Es sieht so aus, als würde "Geschwindigkeit übertragen" werden.

• Problematisierung: Wird also wirklich die Geschwindigkeit weiter gegeben? Bleibt die Geschwindigkeit konstant? Ein qualitatives Experiment mit unterschiedlichen Massen zeigt ein unübersichtliches Ergebnis: beide Gleiter sind nach dem Stoß in Bewegung.

• Der Lehrer schlägt einen inelastischen Stoß gleicher Massen vor, von denen eine vor dem Stoß ruhte. Wird jetzt auch die Geschwindigkeit übertragen? Schon der qualitative Versuch widerspricht dem. Die beiden Massen bleiben aneinander "kleben", vielleicht haben die Schüler den Eindruck, dass die Geschwindigkeit halbiert wurde. Vielleicht schlagen sie wieder einen messenden Versuch vor.

• Ein Lichtschrankenexperiment zeigt exakte Halbierung der Geschwindigkeit.

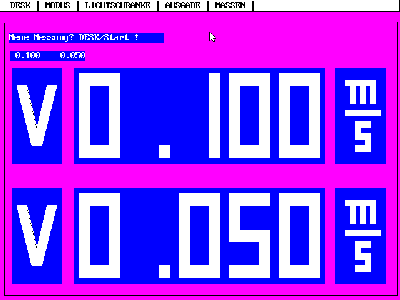  Inelastischer Stoß eines Gleiters mit einem ruhenden gleicher Masse, gemessen mit Lichtschranken. "Geschwindigkeit wird nicht übertragen". Der vereinigte Körper mit doppelter Masse hat nur noch halbe Geschwindigkeit.

• Aha, Geschwindigkeit wird sicher nicht übertragen. Aber, was hat sich noch verändert? Der Körper, der sich nach dem Stoß bewegt, hat doppelte Masse.

• Doppelte Masse - halbe Geschwindigkeit, ist etwas unverändert geblieben? Die Schüler schlagen in der Regel vor, dass das Produkt beider konstant geblieben ist.

• Gilt das immer? Ein Lichtschranken-Versuch mit einem ruhenden Gleiter doppelter Masse zeigt als gemeinsame Geschwindigkeit der dreifachen Masse 1/3 der ursprünglichen Geschwindigkeit, ein Versuch mit einem stoßenden Gleiter doppelter Masse zeigt 2/3 der ursprünglichen Geschwindigkeit.

• Tatsächlich: Das Produkt von Masse und Geschwindigkeit ist in allen Fällen unverändert geblieben. Es wird nicht die Geschwindigkeit weiter gegeben, sondern eine völlig neue Größe, die definiert ist als die eben beobachtete Erhaltungsgröße. Sie wird Impuls p genannt.

• Im vorliegenden Fall, wo ein Gleiter der Masse m den Impuls p besaß und übertrug, hängt der Impuls p mit dem Produkt von Masse und Geschwindigkeit zusammen, und es gilt :  p = m.v.  (So soll vermieden werden, dass die Schüler den Impuls als Produkt auffassen bzw. automatisch davon ausgehen, dass nur ein Körper mit Masse einen Impuls haben könnte. Auch eine elektromagnetische Welle besitzt ja, wie wir wissen, einen Impuls, der nicht (automatisch) mit einer Masse zusammenhängt.)

• Wird auch bei elastischen Stößen der Impuls p weitergegeben? Das kann nicht so einfach gehen, weil ja beide Massen nach dem Stoß in Bewegung sind.

• Mit zwei Lichtschranken werden bei einem elastischen Stoß von Gleitern gleicher Masse 3 Geschwindigkeiten gemessen, oder gar 4 wie in den nachfolgenden Bildern. Vielleicht schlagen Schüler schon die Erhaltung der Summe der Impulse vor. Das Versuchsergebnis widerspricht der Vermutung, es sei denn, man verwendet unterschiedliche Vorzeichen der Impulse je nach Bewegungsrichtung. Dann aber bestätigt sich das Versuchsergebnis sehr gut. Der Impuls wird als Vektorgröße eingeführt: p = m.v, Impuls und Geschwindigkeit sind immer gleichgerichtete Vektoren. Wegen der Richtungsaussage enthält der Impuls mehr Information als die kinetische Energie, die auch von m und v abhängt.

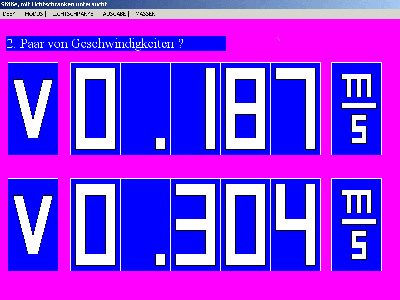Stoß zweier einander entgegen laufender Gleiter auf der Fahrbahn mit gleichen Massen, mit Lichtschranken vermessen. Hier die Beträge der gemessenen Geschwindigkeiten vor dem Stoß. Aus der Impulssumme lässt sich die Masse herauskürzen und liefert die Geschwindigkeitssumme (0,304 m/s - 0,187 m/s = ) 0,117 m/s

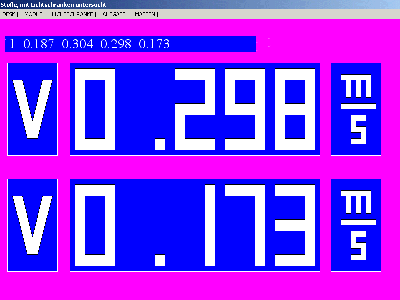Geschwindigkeiten desselben Versuchs nach dem Stoß: Die Geschwindigkeitssumme ist hier 0,125 m/s. Die Abweichung der beiden Geschwindigkeitssummen beträgt in diesem Versuch ca. 7 %, häufig ist die Abweichung geringer. Die Genauigkeit hängt davon ab, dass die Fahrbahn horizontal justiert wurde, und dass die Gleiter beim Anschieben keinen seitlichen Stoß bekamen. Mit etwas Übung lässt sich das perfektionieren. Häufig wirkte es sich günstig aus, wenn die beiden Gleiter mit der Hand nicht gleich durch die Lichtschranken geschossen wurden, sondern erst gegen die Prallböcke an den Enden der Fahrbahn.

• Der Versuch könnte auch mit unterschiedlichen Massen durchgeführt werden. Ich habe darauf meistens verzichtet.
• Es wird auf den Gesamtimpuls hingelenkt und formuliert:

IES:      Bei elastischen wie inelastischen Stößen bleibt der Gesamtimpuls konstant bzw. "erhalten".

• Mit Münzstößen werden die quantitativen Versuche wiederholt und diskutiert, wie sich die Impulsvektoren dabei auswirken (Stoß gleicher Massen, "klein gegen groß", "groß gegen klein", elastischer Stoß gegen eine feste Wand). Es kommt darauf an, dass die Schüler mit den Impulsvektoren anschaulich umzugehen lernen, z.B. mittels einer Serie von Zeichnungen, in die sie die Vektorpfeile  passend zu den jeweiligen beobachteten Bewegungsrichtungen einzeichnen. Es wird klargemacht, dass der Impuls nicht nur Aussagen über den Betrag der Geschwindigkeit und Masse enthält, sondern auch über die Bewegungsrichtung.

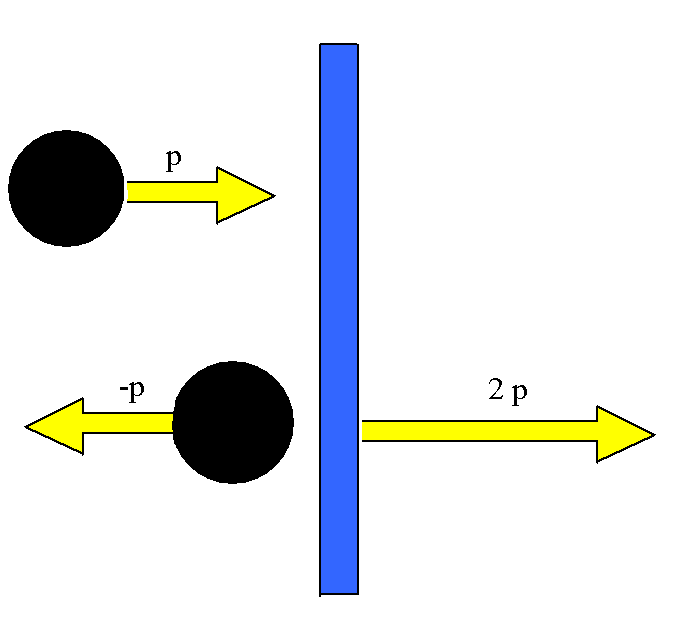  Vektordiagramm für Stoß gegen eine feste Wand (entsprechend einem Stoßpartner beliebig hoher Masse) Das Vektordiagramm erklärt, weshalb die Wand den doppelten Impuls aufnimmt (und später: so gut wie keine Energie). Würde man hier m und v ins Spiel bringen, würden die wichtigen Aspekte verschleiert werden.

Auch mit dem Sonarmeter lässt sich der IES eindrucksvoll nachweisen. Ich habe es aber immer vorgezogen, zuerst darauf zu verzichten. Der Versuch ist zu einer Wiederholung geeignet und zeigt eindrucksvoll noch eine Besonderheit, nämlich, dass der Gesamtimpuls sogar während des Stoßes konstant bleibt. Der Versuch scheint mir weniger gut geeignet zu sein, den Zusammenhang mit Masse und Geschwindigkeit zu erarbeiten.

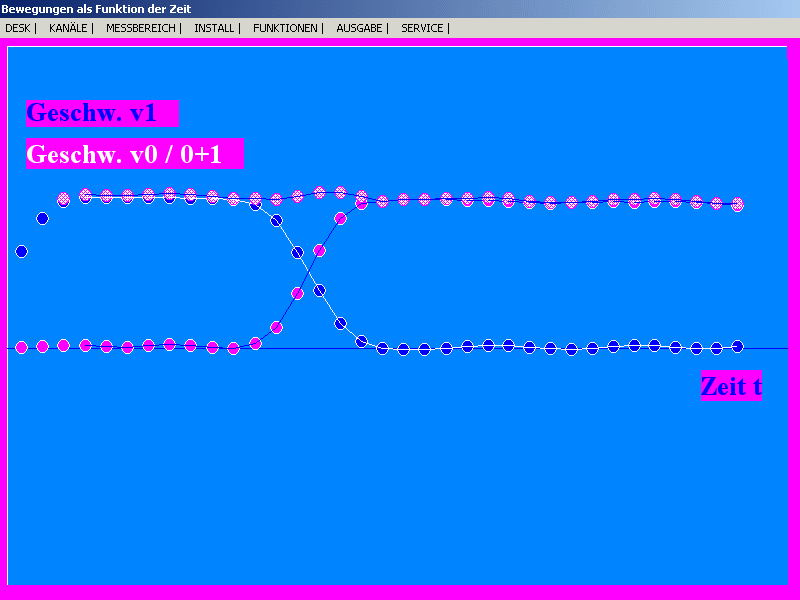Realer Stoß zweier Gleiter gleicher Massen auf der Luftkissenfahrbahn von denen einer vor dem Stoß ruhte, gemessen mit zwei gegenläufig schauenden Sonarmetern. Man erkennt hier, dass die Geschwindigkeitssumme sogar während des Stoßes (recht gut) konstant ist. Eine solche Darstellung zu "lesen" müssen Schüler allerdings erst lernen.

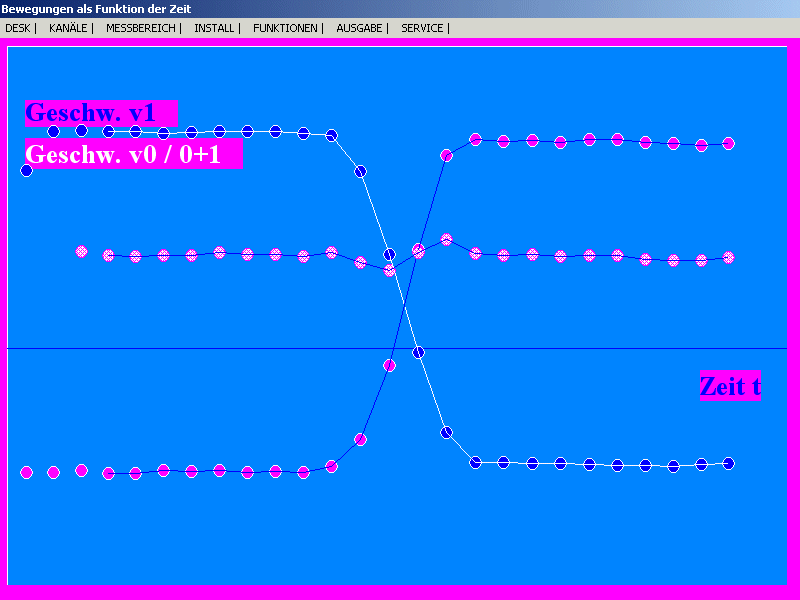Realer Stoß zweier Gleiter gleicher Massen auf der Luftkissenfahrbahn, die vor dem Stoß aufeinander zu fuhren, gemessen mit zwei Sonarmetern. Auch hier ist die Geschwindigkeitssumme (mittlere Kurve) sogar während des Stoßes (recht gut) konstant. So eindrucksvoll diese Bilder sind, das Erhaltungsphänomen und der Bilanzcharakter des Impuls-Erhaltungssatzes kommen m.E. beim Versuch mit Lichtschranken besser heraus. Mit zwei Infrarot-Bewegungsmesswandlern lassen sich die Versuche auch als Schülerversuche durchführen (Vgl. Buch "Schülerversuche mit PC ... ). Die leichte scheinbare Änderung des Gesamtimpulses während des Stoßes kommt möglicherweise durch ein Nachwippen des Schallreflektors auf den Gleitern zustande.

• Es wird auf den Bilanzcharakter des IES hingewiesen, vor allem auch darauf, dass man überhaupt nicht wissen muss, was während des Stoßes passiert, welche Kräfte dabei wirken. Der IES ist auf jeden Fall zwingend.

• Aufgaben zu inelastischen Stößen zeigen, dass man mit dem IES Vorhersagen machen kann.

  Ich habe es mir angewöhnt, auch schon durch die Symbolik auszudrücken, dass Impulse grundlegender sind als Geschwindigkeiten: Wenn ein Impuls vorkommt, wird er immer mit p bezeichnet, nie durch Masse und Geschwindigkeit ausgedrückt. Erst, wenn nach der Geschwindigkeit gefragt ist, wird im letzten Schritt der erhaltene Impuls p nach der Geschwindigkeit aufgelöst. Nach einer Gewöhnungszeit (in der die vertrauten Geschwindigkeiten nicht mehr vorkommen) erspart dies den Schülern viel Schreibarbeit und schafft Übersicht.

• Dann wird als weiterer Erhaltungssatz der Energie-Erhaltungssatz wiederholt. Er braucht nicht neu hergeleitet werden, da sich die Schüler aller Erfahrung nach an ihre Mittelstufenkenntnisse von ihm erinnern. Er vertieft das Phänomen der Erhaltung.

• Erst jetzt können auch elastische Stöße mit IES und EES durchgerechnet werden. Auch hier vereinfacht der Gebrauch des Impulssymbols und E_kin = p²/2m Schreibarbeit und Rechnung. Insbesondere könnte es interessant sein, zu einem Lichtschranken-Versuch mit einem elastischen Stoß bei 4 Geschwindigkeiten nur 3 Geschwindigkeiten abzulesen und durch Rechnung zu überprüfen, ob sich auch die 4. Geschwindigkeit richtig ergeben hat  (Vgl. Rechentechnik zum elastischen Stoß).

• Nicht für eine durchschnittliche Klasse, aber doch für gute Schüler ist eine Methode geeignet, mit der man Stöße (bei einfachen Zahlenwerten) im Kopf rechnen kann, wenn man ins Schwerpunktssystem übergeht.

.

.