|
Elastische Stöße im
Schwerpunktssystem
|
|
Im
Schwerpunktssystem ist der Gesamtimpuls 0.
|
Deshalb sind IES und EES im Schwerpunktsystem sehr
einfach (eindimensional betrachtet):
Die Rechnung soll hier ein einziges Mal formal
durchgeführt werden. Einfache Beispiele lassen sich dann im Kopf lösen.
(1) IES: p + P = p' + P' = 0
(2) EES: p2/2m + P2/2M =
p'2/2m
+ P'2/2M
(1) in (2) liefert:
p2 (1/2m + 1/2M) = p'2 (1/2m
+ 1/2M)
oder p2 =
p'2 mit den beiden Lösungen
p = p' und p = -p'.
Die erste Lösung entspricht keinem Stoß, die zweite einer
Richtungsumkehr unter Beibehaltung des Impulsbetrags. Der zweiten Lösung
entspricht auch P = -P'.
Man kann sich also merken:
|
Beim elastischen
Stoß im Schwerpunktssystem kehren sich beide Impulse um.
|
Die Arbeit des Schülers besteht nur noch darin die Geschwindigkeit
vS des Schwerpunkts zu ermitteln und in das
Laborsystem zurückzutransformieren. Der Schwerpunkt ist dadurch
gekennzeichnet, dass man sich in ihm die gesamte Masse
konzentriert denken kann. Der Schwerpunktsimpuls entspricht also dem
Gesamtimpuls im Laborsystem. Es gilt daher:
PS
= pL + PL, also
(m+M) vS = mvL + MVL,
und damit
vS =
(mvL + MVL)/(m+M)
Der Index L kennzeichnet dabei die Werte im Laborsystem.
In der Regel (und bei einfachen Werten) wird man die
Schwerpunktsgeschwindigkeit erraten.
Mit v'L = v ' + vS und V'L
= V' + vS erfolgt die Rücktransformation ins
Laborsystem.
So einfach die Algebra dieses Verfahrens ist, und damit
auch das Verständnis für die Schüler, so schwierig ist wohl für die
Schüler der Wechsel des Koordinatensystems.
Auf jeden Fall sollten nach der Rücktransformation
Impuls- und Energieerhaltung auch im Laborsystem überprüft werden.
Zahlenbeispiele:
|
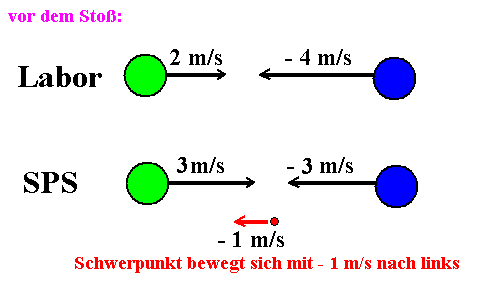
1. Beispiel:
gleiche Massen vL
= 2 m/s VL = - 4 m/s
Eigentlich kommt man ohne Rechnung
aus. Man kann sich alle Werte an der Zeichnung überlegen.
Dann muss die
Schwerpunktsgeschwindigkeit sein: vS = - 1 m/s ;
die Rechnung hätte das gleiche geliefert:
vS = (m .vL+ m
.VL)/2m = (vL+VL)/2 = - 1
m/s: Relativ zum Schwerpunkt gelten also die
Geschwindigkeiten v = 3 m/s und V = -3 m/s, und dann auch v'
= - 3 m/s und V' = 3 m/s. (Gesamtimpuls im SPS = 0!)
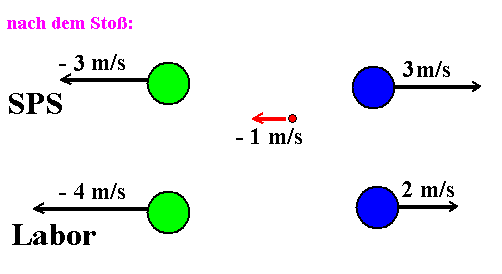
Daraus ergeben sich die
Geschwindigkeiten im Laborsystem:
vL' = vS + v' =
- 4 m/s und VL' = vS + V' = 2 m/s:
Beide Körper "tauschen" ihre Geschwindigkeiten aus.
|
|
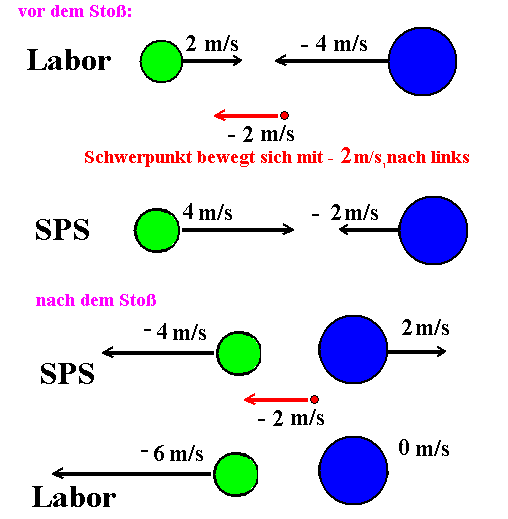 |
2. Beispiel:
M = 2m
vL = 2 m/s VL
= - 4 m/s
Man kann fast schon raten,
was dann die Schwerpunkts-Geschwindigkeit ist:
vS = (m.vL+
2mVL)/3m = (vL+2VL)/3
= - 2 m/s
Vor dem Stoß gilt
im Schwerpunktssystem : v = vL
- vS = 4 m/s und V =
VL - vS = - 2 m/s.
(Gesamtimpuls im SPS = 0!)
Nach dem Stoß im
Schwerpunktsystem: v' = - v = -
4 m/s und V' = - V = 2 m/s
Dementsprechend betragen die
Geschwindigkeiten nach dem Stoß im Laborsystem:
vL' = vS
+ v' = - 6 m/s und VL' = vS
+ V' = 0 m/s:
Der Körper mit der Masse m
trägt jetzt den gesamten Impuls nach dem
Stoß in negative Richtung, also in die Richtung,
die die größeren Masse vor dem Stoß hatte,
die auch noch schneller war und den deutlich
überwiegenden Impuls hatte.
Die ausschließliche Rechnung
im Laborsystem hätte das gleiche geliefert.
|
|
|
|
|


