Dieser Text steht im Zusammenhang mit dem PC-Simulationsprogramm LEISTRES, das geeignet ist, das Phänomen der Resonanz quasi im Schülerversuch von den Schülern erarbeiten zu lassen. Ihm liegt folgendes, einem bekannten Versuch entsprechendes Modell zugrunde: An einer Schraubenfeder ist eine Masse m aufgehängt bzw. auf der Luftkissenfahrbahn gleitet eine Masse m, die zwischen 2 Federn gespannt ist. Der Aufhängepunkt bzw. ein Ende einer der beiden Federn auf der Fahrbahn wird z.B. mittels eines Exzenters periodisch auf-und-ab bzw. hin-und-her bewegt. Es liegt also die sog. Aufhängungskopplung vor.
|
|
|
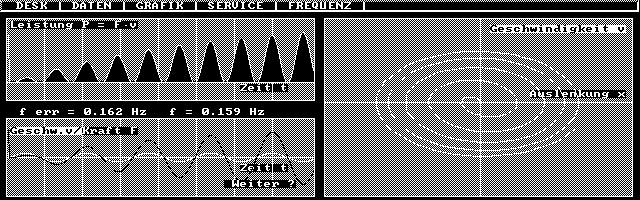
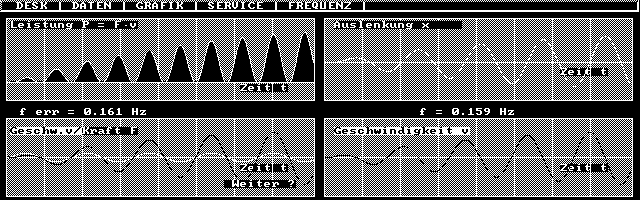
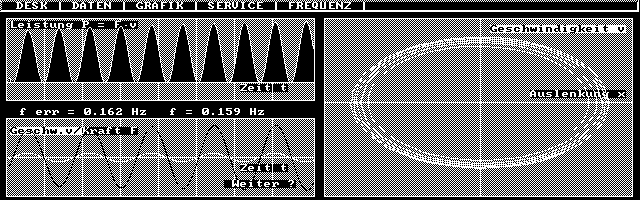
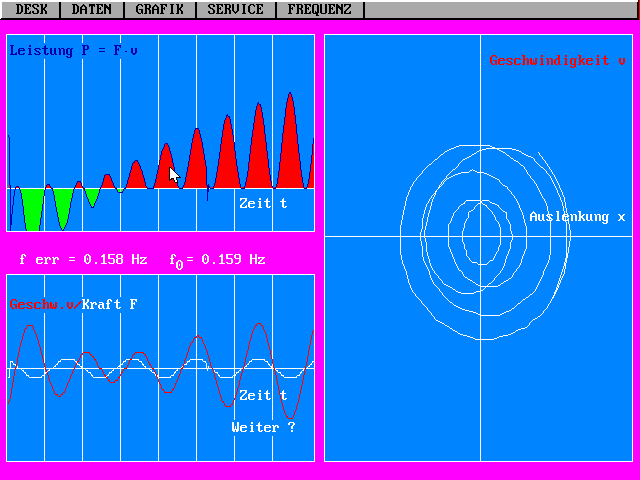
| Mit LEISTRES erzeugte Graphen eines Einschwingvorgangs sehr nahe der Resonanz. Erregende Kraft und Geschwindigkeit sind nach einiger Zeit gut in Phase, d.h. es wird fast immer dem Pendel Energie zugeführt, die zu einer Amplitudensteigerung führt, wie an den Graphen links und im Phasendiagramm rechts erkennbar ist. Wegen der Amplitudenzunahme ist das Phasendiagramm noch eine Spirale. Sie geht in einen Kreis bzw. eine Ellipse über (Grenzzyklus). Wenn - bei geeigneten Maßstäben der Achsen - ein Kreis entsteht, zeigt er konstante Radius die Erhaltung der Gesamtenergie an, für die der Radius ein Maß ist. |
Einerseits [1] wird das Amplitudenmaximum als Kriterium für Resonanz gesehen ("Anmplitudenresonanz"). Dann gilt: Abhängig von der Dämpfung findet Resonanz statt, wenn die Erregerfrequenz ungefähr mit der Eigenfrequenz des Pendels übereinstimmt. Dann ist die Phasenverschiebungen zwischen Erregerschwingung und erzwungener Schwingung ungefähr -90°. Bei Dämpfung sind diese etwas komplexeren Verhältnisse leider nicht leicht überschaubar.
Andererseits [2] wird maximale Leistungsaufnahme (Energieaufnahme) während einer Periode als Kriterium für Resonanz gesehen ("Energieresonanz"). Diese Definition hat den Vorteil, daß (1) Resonanz immer dann erfolgt, wenn die Erregerfrequenz exakt mit der Eigenfrequenz übereinstimmt. Dann ist die Phasenverschiebungen zwischen Erregerschwingung und erzwungener Schwingung exakt -90°. Das Amplitudenmaximum liegt dann allerdings bei einer Frequenz, die etwas geringer als die Eigenfrequenz ist. Diese Definition hat weiter den Vorteil (2), daß die Resonanz jetzt leicht deutbar ist, nämlich gerade durch die maximale Energieübertragung vom Erreger an das Pendel.
Etwas liebäugelnd mit der zweiten Definition ("Energieresonanz") wird deshalb in den 'Versuchen' mit dem Programm LEISTRES die Phasenverschiebung zwischen erregender Kraft und Geschwindigkeit untersucht. Das Produkt der beiden Größen ist die Leistung P = F.v, die vom Erreger an das Pendel übertragen wird. Auch für Liebhaber der "Amplitudenresonanz" ist das Programm zu gebrauchen: es wurden Formulierungen gewählt, die verträglich sind mit beiden Definitionen der Resonanz.
|
|
|
||
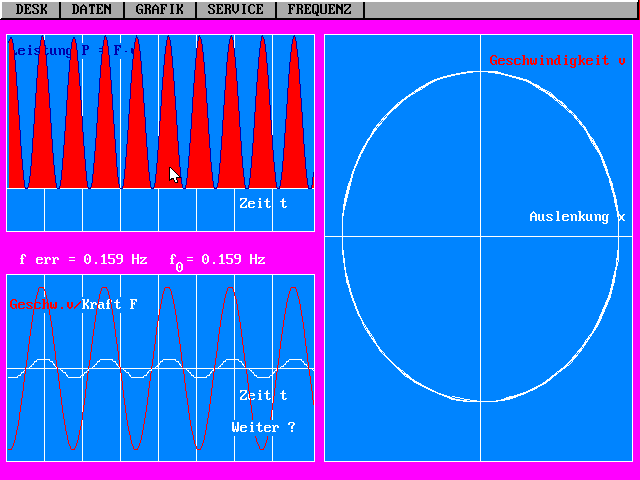
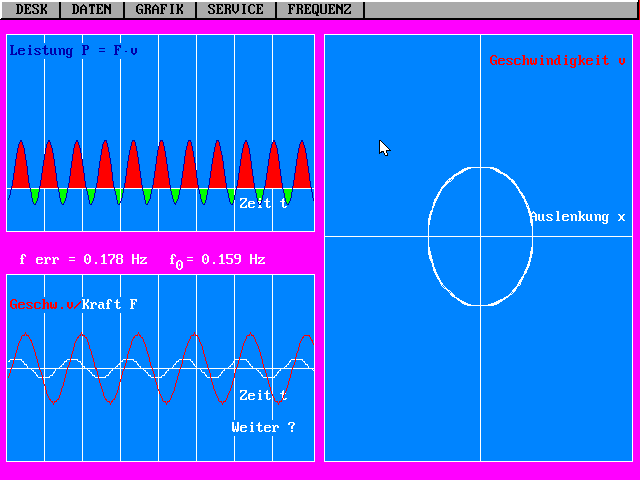
| Phasenverschiebungen zwischen erregender Kraft und Geschwindigkeit im Resonanzfall: F und v in Phase (Graphik unten links): maximale Leistungsübertragung (Graphik oben links). | Phasenverschiebungen zwischen erregender Kraft und Geschwindigkeit außerhalb des Resonanzfalls: F und v nicht in Phase: In einer Periode wird ein Teil der gelieferten Energie wieder an den Erreger zurück gegeben. |
1. Bei sehr kleinen Erreger-Frequenzen ist die erregende Kraft F sehr klein (Feder wenig beansprucht, da Amplitude A ≈ Hub H wegen vernachlässigbarem Einfluß der Trägheit des schwingenden Körpers; außerdem ist die Phasenverschiebung zwischen Geschwindigkeit und erregender Kraft gerade so, daß im Zeitmittel über eine Periode die geringe aufgenommene Leistung wieder an den Erreger zurückgeliefert wird.
2. Bei sehr großen
Erreger-Frequenzen sind wegen der großen Wirkung der
Trägheit die Amplituden von Auslenkung und Geschwindigkeit sehr
klein und deshalb ist auch die Leistung P klein. Außerdem ist die
Phasenverschiebung zwischen Geschwindigkeit und erregender Kraft
gerade so, daß im Zeitmittel über eine Periode die geringe
aufgenommene Leistung wieder an den Erreger zurückgeliefert wird.
3. Im Resonanzfall,
wenn also die Erregerfrequenz ungefähr mit der Eigenfrequenz des
Pendels übereinstimmt, sind Kraft F und Geschwindigkeit v in Phase
(nach der 2. Definition sogar exakt bei Übereinstimmung der
Frequenzen). Die Leistung P = F.v ist zu allen Zeiten
nichtnegativ; zu fast allen Zeiten wird dem Pendel vom Erreger
Energie zugeführt. Diese dient entweder dazu, die Amplitude zu
erhöhen, oder wird, wenn der stationäre Zustand erreicht ist,
sofort wieder vollständig als Reibungswärme an die Umgebung
abgegeben.
Die Resonanzfrequenz kann im Sinn der "Energieresonanz" auch exakt definiert werden als "die Frequenz, bei der erregende Kraft F und Geschwindigkeit v in Phase sind". (Man kommt damit weg von den unbefriedigenden Schul-Definitionen nach der 1. Methode, wie "wenn die Erregerschwingung der erzwungene Schwingung um ungefähr 90° vorauseilt", oder "wenn die Erregerfrequenz ungefähr mit der Eigenfrequenz übereinstimmt". Falls Dämpfung vorliegt, gelten die üblichen Faustregeln ja nicht mehr exakt; die Abweichung zwischen beiden Definitionen macht sich ebenfalls mit zunehmender Dämpfung stärker bemerkbar.
Die Betrachtung des Energieaustausches zwischen Erreger und Pendel erklärt zugleich auch das Anwachsen der Amplitude im Resonanzfall und die konstante Amplitude im stationären Schwingfall (nach dem Einschwingvorgang).
Außer der Aufhängungskopplung, die sich bei mechanischen Experimenten leicht realisieren läßt, gibt es noch andere Kopplungsarten. Die "Kraftkopplung" ist sehr verwandt. Die momentane Dehnung der Feder, bestimmt durch Hub H und Amplitude A, hängt ja mittels des Hookeschen Gesetzes eng mit der dehnenden (erregenden) Kraft F zusammen. Hier wird die Zeitabhängigkeit der Kraft und nicht der Erregerauslenkung vorgegeben. Bei der "Strom- oder Geschwindigkeitskopplung" geht die Zeitabhängigkeit der Geschwindigkeit des 'Erregers' ein, bei der "Beschleunigungskopplung" die Zeitabhängigkeit der Beschleunigung des 'Erregers'. Beschleunigungskopplung spielt eine Rolle beim Seismographen, Stromkopplung beim elektromagnetischen Serienresonanzkreis, Auslenkungskopplung ist in der Mechanik am leichtesten experimentell zu realisieren. Auch beim elektromagnetischen Parallelresonanzkreis hängt die Form der Resonanzkurve davon ab, ob der Schwingkreis galvanisch, induktiv oder kapazitiv an den Erreger angekoppelt ist.
Im Programm LEISTRES ist zwischen den 4 Kopplungsarten durch Menuepunkte zu wählen.
- x(t) und v(t)
-
F(t), v(t) und P(t)
-
Phasendiagramm (besonders eindrucksvoll beim Anfachen oder Abklingen einer gedämpften Schwingung mit Entstehung eines Grenzzyklusses)
-
Resonanzkurve
-
gemischte Darstellungsformen.
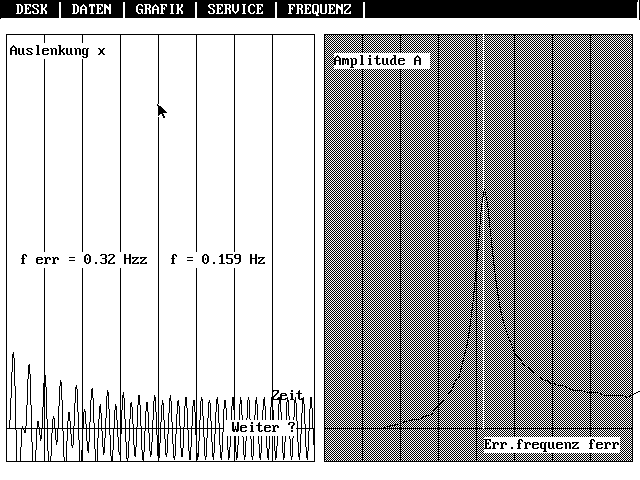
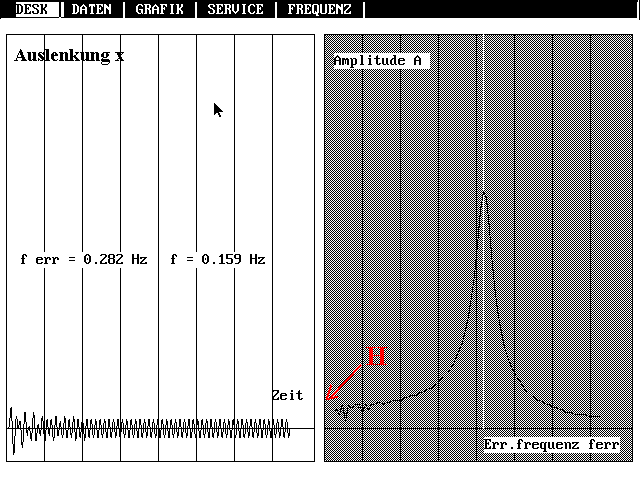
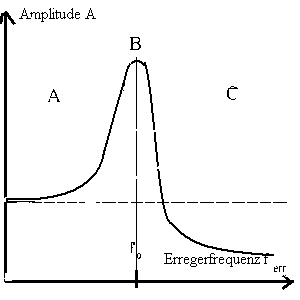
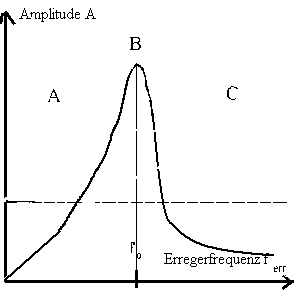
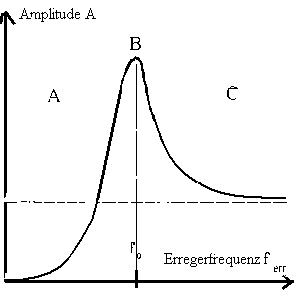
Die Resonanzkurve ist stark von
der gewählten Kopplungsart abhängig. Gerade die charkteristischen
Unterschiede werden etwa beim Seismographen genutzt. Bei der
Darstellung der Resonanzkurve werden gegenübergestellt die
zeitabhängige Auslenkung x(t) und der Wert der Amplitude A, der
sich nach Abschluß des Einschwingvorgangs einstellt, und der dann
erst in die Resonanzkurve übernommen wird. Der Benutzer bekommt
also stets den (fast) ganzen Einschwingvorgang vorgeführt, bis ein
Punkt der Resonanzkurve gezeigt wird.
|
B ZUR THEORIE DER VERSCHIEDENEN KOPPLUNGSARTEN BEI DER ERZWUNGENEN SCHWINGUNG |
| m x•• + D x + ß x•= F(t) |
In der Mechanik haben die Parameter folgende Bedeutung:
-
m : schwingende Masse
-
D : Rückstellkonstante der Feder (Federhärte)
-
ß : Dämpfungskonstante
-
F : erregende Kraft, die an der schwingenden Masse angreift.
Die Zeitabhängigkeit der
erregenden Kraft wird vom Erreger vorgegeben. Ist F(t)
proportional zu sin(ωt) oder cos(ωt) mit der (Kreis-)Frequenz ω,
ist komplexe Rechnung üblich: F(t) = F0 eiωt
und der komplexe Ansatz x = A.eiωt+iφ
führt zur Phasenverschiebung φ zwischen Kraft F und Auslenkung x
und zur Amplitude A:
| A = F0 / m [
(ω02-ω2)2
+ (ß/m)2 ω2
]-½
mit ω0 = √ ( D/m) |
Der Term F(t) kann nun, je nach Kopplung, auf verschiedene Weisen zustandekommen:
1. Kraftkopplung:
Eine äußere Kraft F greift direkt
an der schwingenden Masse an. Dann gilt die allgemeine Formel
unverändert mit konstanter Amplitude F0 der erregenden
Kraft. Charakteristisch ist das asymptotische Verhalten der
Amplitude in Abhängigkeit von der Erregerfrequenz ω:
| A ~ F0 / ( mω02 ) { 1 + ( ω / ω0 )2 (2 - (ß/m)2 ) } | für ω -> 0 |
| A ~ F0 /( m ω2 ) | für ω -> ∞ |
Die Frequenz für das Amplitudenmaximum ergibt sich aus der Ableitung von A nach der Frequenz [1] zu
Sie stimmt bei kleiner Dämpfung ß ungefähr mit der Eigenfrequenz ω0 überein. Bei dieser Frequenz ist die Phasenverschiebung φ zwischen Auslenkung und erregender Kraft bekanntlich nur im Grenzfall verschwindender Dämpfungskonstante -90°.
Hier bewegt sich der
Aufhängungspunkt der Feder sinus- oder cosinusförmig, etwa gemäß y
= H sin(ωt). H wird oft Hub genannt.
| A ~ H { 1 + ω2 [...]} | für ω -> 0 |
| A ~ H (ω 0 / ω )2 | für ω -> ∞ |
3. Geschwindigkeits-Kopplung (Strom-Kopplung):
Für F(t) wird hier der Ansatz F(t) = -α y•(t) gemacht, wobei für y(t) etwa gelte: y(t) = H. cos(ωt).
F = α ω H sin(ωt)
In den früheren Formeln ist F0 durch α ω H zu ersetzen. Dies hat Einfluß auf das asymptotische Verhalten bei kleinen und großen Frequenzen und auf die Resonanzfrequenz:
| A ~ αω H /( m ω02 ) prop. ω | für ω -> 0 |
| A ~ αH / ω prop. 1 / ω | für ω -> ∞ |
Geschwindigkeits-(Strom-)Kopplung ist anzuwenden bei einem Serienschwingkreis mit hintereinandergeschaltetem Widerstand R, Induktivität L und Kapazität C [3]. Da sich die Teilspannungen addieren, gilt nach Zeitableitung:
.
L Q•• + 1/C Q + R Q•= U(t)
Im Modell läßt sich das
Zustandekommen eines solchen Terms leicht verstehen: Danach
befinde sich der Aufhängepunkt des Pendels in einem Bezugssystem
S', das relativ zum Laborsystem S mit y = H . sin(ωt) bewegt
werde. Ein mit S' mitbewegter Beobachter registriert die
Koordinate x' und ihre Ableitungen, auch die Reibungskraft ßx' und
die Rückstellkraft -Dx'. Im Laborsystem gilt aber mit x = y + x'
die Bewegungsgleichung
m x•• + D x' + ß x'•= 0
Im beschleunigten System S' wird daraus:
m x'•• + D x' + ß x'• = - m y••
Das Modell entspricht der Situation des Seismographen: Der Aufhängepunkt des Pendels wird durch die Erdbebenwellen beschleunigt, aber auch der Beobachter sitzt im beschleunigten Bezugssystem. Die Resonanzfrequenz ist also sehr viel tiefer als die Frequenz der Erdbebenwellen zu wählen, damit die Amplitude der erzwungenen Schwingung mit dem gesuchten Hub H übereinstimmt!
Die nachfolgenden Skizzen veranschaulichen noch einmal das asymptotische Verhalten für die drei bzw. vier Fälle:
|
Kraftkopplung |
Aufhängungskopplung |
Geschwindigkeitsk. |
Beschleunigungskopplung |
Grenzübergang |
||
|
A ~ F0/(m ω02) . {1+ω2 [...]} |
|
A prop. ω |
A ~ H ( ω2 / ω02 ) . { 1 + ω2 [...]} |
für ω -> 0 |
||
|
A ~ F0/(m2) |
A ~ H ( ω0 / ω )2 |
A prop. 1 / ω |
A ~ H |
für ω -> ∞ |
||
 |
 |
 |
Vgl. Simulation der Beschleunigungskopplung und Simulation der Aufhängungskopplung
| ½ m x• 2 + ½ D x2 = Eges |
bzw. nach Multiplikation mit 2/mD:
|
x•2 / D + x2 / m = 2 Eges /(mD)
|
Bei konstanter Gesamtenergie ist das
die Gleichung einer Ellipse mit den Halbachsen √D und √m. Bei
geeigneter Skalierung ist die Ellipse ein Kreis, dessen konstantes
Radiusquadrat der konstanten Gesamtenergie entspricht. Zunahme
(Abnahme) des Radius entspricht dann Zunahme (Abnahme) der
Gesamtenergie. Die Aussagen gelten nicht mehr, wenn für die
potentielle Energie kein quadratisches Gesetz gilt.
Das Auftreten einer Ellipse bzw. eines Kreises ist also im einfachsten Fall ein Nachweis des Energie-Erhaltungssatzes.
zurück
|
|
| Der Einschwingvorgang führt zu wachsenden Amplituden. Grund ist die Phasenverschiebung zwischen Erregerkraft F und Geschwindigkeit v, die zu einer stets zunehmenden Leistungsübertragung (P = F.v >= 0 ) auf das Pendel führt. |
|
|
|
| Grenzzyklusverhalten einer erzwungenen Schwingung im Phasendiagramm: Allmählich stellt sich für den stationären Schwingfall eine konstante Amplitude ein. Es wird quasi ständig Energie (Leistung) zugeführt (P = F.v > = 0), die aber kaum mehr zur Vergrößerung der Amplitude genutzt wird als vielmehr zum Ausgleich der Dämpfungsverluste. Maximale Amplitude ist erreicht, wenn die Verluste soweit angewachsen sind, dass die in jeder Periode zugeführte Energie gleich der durch die Dämpfung verlorenen Energie ist. |
|
|
|
| Resonanzkurve bei Beschleunigungskopplung. Außerdem ist der Einschwingvorgang erkennbar; erst wenn die stationäre Schwingung erreicht ist, wird die Amplitude in die Resonanzkurve eingetragen. |
|
|
| Resonanzkurve für Aufhängungskopplung. Außerdem ist der Einschwingvorgang erkennbar; erst wenn die stationäre Schwingung erreicht ist, wird die Amplitude in die Resonanzkurve eingetragen. |
|
|
|
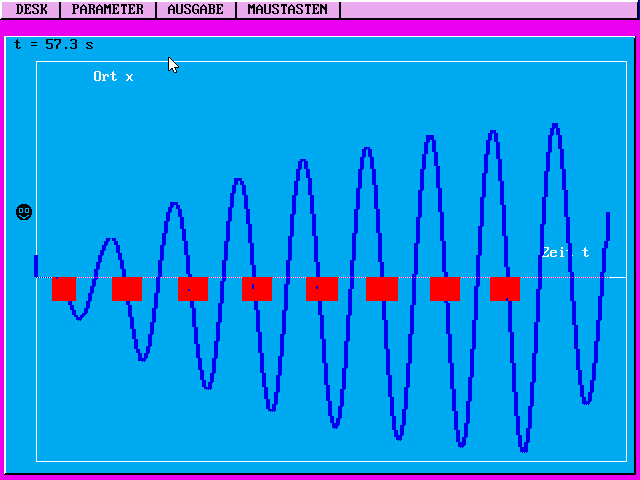
| Mit dem PC-Programm ERZWUSCH erzeugter
Einschwingvorgang eines simulierten Pendels (links ist der
Pendelkörper sichtbar). Der Schüler versucht ohne Instruktion,
allein durch Probieren, durch Tastendruck das Pendel in
Schwingungen zu versetzen. Solange er eine Taste gedrückt hält,
wird eine konstante Kraft auf den Pendelkörper ausgeübt. Die
Kraft ist auf dem Bildschirm rot markiert. Hier gelang es
offenbar dem Nutzer überwiegend, den Krafteinsatz optimal zu
terminieren, so dass die Amplitude durch geeignete Energiezufuhr
anwuchs. Der Schüler sollte daraus ableiten, dass die
Energiezufuhr
erfolgen muss, damit eine Schwingung optimal "aufgeschaukelt" wird. |
|
|
|
| Mit LEISTRES erzeugte Graphen eines Einschwingvorgangs sehr nahe der Resonanz. Erregende Kraft und Geschwindigkeit sind nach einiger Zeit gut in Phase, d.h. es wird fast immer dem Pendel Energie zugeführt, die zu einer Amplitudensteigerung führt, wie an den Graphen links und im Phasendiagramm rechts erkennbar ist. Vor dem Beginn des Einschwingvorgangs war das Pendel mit einer anderen Frequenz schon in Bewegung. Es musste erst Energie an den Erreger abgeben, bevor eine neue Schwingung mit der angegebenen Frequenz angefangen werden konnte. |
[1] Classical Dynamics of particles and systems / J.B. Marion - New York; London - 1965
[2] Physik:
eine Einführung in Experiment und Theorie, Bd.1 Mechanik / S.
Brandt; H.D. Dahmen - Berlin; Heidelberg; New York; Tokyo - 1984
[3] Physik:
eine Einführung in Experiment und Theorie, Bd.2 Elektrodynamik /
S. Brandt; H.D. Dahmen - Berlin; Heidelberg; New York; Tokyo -
1986
.
.
( Zeichensatz korrigiert 2014 )