Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig- keiten im Physik-UR An- schauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2018

Elektromagnetische Induktion verstehen - eine Unipolar-Induktionsmaschine Das Hering'sche Paradoxon - eine Gegendarstellung zum Wikipedia-Artikel

Eine Analyse

Neubearbeitung Mai 2013

Einführung Hinweis auf die Situation beim Leiterstab, der auf einem U-förmigen Leiterbügel im Magnetfeld gleitet Untersuchung des in Bewegungsrichtung endlich langen Magneten: die Kräfte auf ein Leitungselektron im Magneten heben sich gegenseitig auf, gesehen vom Laborsystem aus die Kräfte auf ein Leitungselektron im Magneten heben sich gegenseitig auf, gesehen vom Bezugsssystem des Magneten aus Beiträge zur Ringspannung längs einer beliebigen geschlossen Kurve C: Insgesamt 0 Richtige Interpretation der Flussregel für diesen Fall Untersuchung des in Bewegungsrichtung unendlich langen Magneten: die Kräfte auf Leitungselektronen im Magneten heben sich gegenseitig auf keine Wirbel des elektrischen Felds im Bereich der Kurve C: keine Änderung des magnetischen Flusses und kein Beitrag zur Ringspannung vom elektrischen Feld her einziger Beitrag zur Ringspannung als Folge der Lorentz-Kraft: Unipolarinduktion Zusammenfassung Vergleich unterschiedlicher Betrachtungsweisen Hering'sches Paradoxon Literatur

Einführung

Ein Sonderfall einer Unipolar-Induktionsmaschine beschäftigt seit langem immer wieder Autoren von Hochschullehrbüchern zur Elektrodynamik oder von Wissenschaftlern, die Grundsätzliches über die elektromagnetische Induktion verstehen wollen. Leider erscheinen nicht alle Argumente stichhaltig. Es wird hier eine konsistente Betrachtung zusammengestellt, basierend auf den Literaturstellen [1], [2] und [3]. Sie wird u.a. auch deshalb als konsistent angesehen, weil sie von verschiedenen Bezugssystemen her zum jeweils gleichen Ergebnis führt. Für den Leser ist möglicherweise ungewohnt, wann eine Lorentz-Kraft anzusetzen ist, dass die entscheidende Größe bei der Induktion eine Ringspannung (und keine gewöhnliche Spannung/Potenzialdifferenz) ist, und welche Beiträge zur Ringspannung^*) berücksichtigt werden müssen.

Zur Erinnerung: Das Induktionsgesetz in der Form der Flussregel besagt, dass die Ringspannung längs einer geschlossenen Kurve C sich aus der zeitlichen Änderung des magnetischen Flusses ergibt, der die von C eingeschlossene Fläche senkrecht durchsetzt:  

                                                ∫₀ E·ds = - dΦ/dt            (∫₀ : Umlaufsintegral längs der geschlossenen Kurve C)

Wenn das Umlaufsintegral =/= 0 ist, liegt ein elektrisches Wirbelfeld vor. Wenn das zu einer Ringspannung =/= 0 führt, findet also Induktion statt. Ein Induktionsstrom (Ringstrom) setzt eine Ringspannung voraus.

Eine zeitliche Änderung des magnetischen Flusses führt - wenn evtl. auch nicht in allen Bezugssystemen - zu einem Wirbelfeld. Das gilt in dem Bezugssystem der Kurve C oder den lokalen Bezugssystemen längs der Kurve C. In anderen Bezugssystemen gibt es dann u.U. kein elektrisches Wirbelfeld, muss das Induktionsgesetz evtl. anders formuliert werden. (vgl. Ringspannung und Induktion)

.

Hinweis auf die Situation beim Leiterstab, der auf einem U-förmigen Leiterbügel im Magnetfeld gleitet

Für den Fall einer Leiterbrücke, die bei gutem Kontakt auf einem U-förmigen Leiterbügel im Magnetfeld gleitet, wurde der Wirbelcharakter des elektrischen Feldes längs dieser Leiterschleife (in den lokalen Bezugssystemen der Leiterschleife) anderswo gezeigt. Gesehen von der Leiterschleife aus wurde so eine Ringspannung (Umlaufspannung) konventionell erklärt, die Ursache für einen Ringstrom ist. Im Laborsystem, in dem der Leiterbügel ruht, ist das entstehende elektrische Feld kein Wirbelfeld. Dennoch musste man auch hier eine nichtverschwindende Ringspannung erwarten, weil ein Ringstrom beobachtet wird. Der Beweis gelang, indem bei der Definition der Ringspannung zur Verschiebungsarbeit für den geschlossenen Weg auch der Beitrag der Lorentz-Kraft berücksichtigt wurde^*). Man muss hier offenbar vorsichtig sein und akzeptieren, dass die Ringspannung nicht in jedem Bezugssystem an das Vorliegen eines elektrischen Wirbelfelds gebunden ist, dass evtl. auch eine magnetische Lorentz-Kraft beitragen kann.

Hier wird nun ein anderer Fall studiert, bei dem offenbar ein elektrisches Wirbelfeld vorhanden ist, aber keine Ringspannung, und deshalb auch kein Ringstrom. Die Vorüberlegungen weisen schon einen Weg.

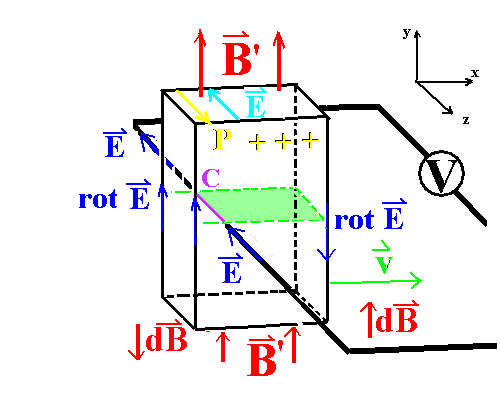Untersuchung des in Bewegungsrichtung endlich langen Magneten: Im Zusammenhang mit der Unipolar-Induktionsmaschien wird folgende Anordnung studiert: Ein magnetisierter, gut leitfähiger Stab bewege sich im Laborsystem K mit konstanter Geschwindigkeit v = v i  in positive x-Richtung, eine Leiterschleife mit einem eingebauten Spannungs- oder Strommesser ruhe im Laborsystem, aber so, dass gut leitende Kontakte auf dem magnetisierten Stab gleiten. Die endliche Länge des Stabs in Bewegungsrichtung sei lx. Zu den diskutierten Fragen gehört: Findet hierbei Induktion überhaupt statt? Wenn ja, was ist die Ursache der Induktion? Gelten die einfachen Regeln für die Induktion (Lorentz-Kraft oder Fluss-Regel) auch hier? Schon bei der ersten Frage gehen die Meinungen in der Literatur weit auseinander. Gerade zur letzten Frage gilt der vorliegende Fall manchmal als Beispiel, dass diese Regeln hier nicht anwendbar seien. Zunächst scheint klar: Wenn wir im Laborsystem argumentieren, dann scheint sich die vom Magnetfeld innerhalb der Leiterschleife durchsetzte Fläche in einer bestimmte Zeit um den grün markierten Bereich mit der Änderungsrate B·lz·v zu vergrößern. Es findet offenbar eine zeitliche Änderung des magnetischen Flusses statt. Wir erwarten ein elektrisches Wirbelfeld gemäß der Flussregel. Es könnte höchstens noch gefragt werden, ob die Flussregel mit der richtigen Kurve richtig eingesetzt wurde.

Abb. 1: Anordnung: Ein quaderförmiger magnetisierter Stab ("Magnet") bewege sich im Laborsystem K mit einer ruhenden Leiterschleife gleichförmig mit v in x-Richtung. Mittels Kontakten gleiten die Leiterenden auf dem gut leitenden Magneten. Versuchs- weise wird hier die Argumentation auf einer Kurve C aufgebaut, die zu einer Änderung des magnetischen Flusses zu führen scheint.

Im Folgenden soll die Situation auf verschiedene Weise untersucht werden. Es wird einerseits versucht, die wirkenden Kräfte zu untersuchen. Es wird sich herausstellen, dass bestimmte von ihnen sich im Magneten gegenseitig kompensieren. Andererseits sollen die Beiträge zur Ringspannung berechnet werden. Auch hier wird es sich herausstellen, dass sie sich in einem bestimmten Fall zu 0 aufaddieren (das hängt dann mit dem Hering'schen Paradoxon zusammen), in einem anderen Fall nicht. In der letzten Situation ergibt sich eine Unipolar-Induktionsmaschine.

Analysieren wir das Problem mit Hilfe der zuständigen speziellen Relativitätstheorie, die die beiden zu betrachtenden Bezugssysteme miteinander verknüpft. Einerseits braucht man das Bezugssystem K', in dem der Stab ruht. In ihm wird eine magnetische Flussdichte B' mit einer Magnetisierung M' gemessen; ein mögliches elektrisches Feld E' kann in ihm als verschwindend gewählt werden.

Andererseits das Bezugssystem K, in dem die Leiterschleife ruht, das Laborsystem also; die in ihm gemessenen Felder und Kräfte sind alle ohne Strich gekennzeichnet. Die Lorentz-Transformation zeigt dann, wie die Felder zu transformieren sind.

.

Die Kräfte auf ein Leitungselektron im Magneten heben sich gegenseitig auf, gesehen vom Laborsystem aus

Argumentation im Laborsystem K:

Da sich im BZS K der Stab mit der Geschwindigkeit v bewegt, wird man in den nichtrelativistisch genäherten Transformationsformeln  -v erwarten können. Wie üblich sind dann im BZS K magnetische Felder B und M zu messen, aber auch ein elektrisches Feld E. Auch die Kraft auf eine Ladung q im Magneten muss mittransformiert werden; F im BZS K enthält dann als einen Anteil eine Kraft, die durch das (als Folge der Transformation entstehende) elektrische Feld E zustande kommt (und wie eine Lorentz-Kraft nur aussieht, aber keine ist). Außerdem wird sich herausstellen, dass in diesem BZS K auch eine Lorentz-Kraft auf solche Ladungen entsteht.

Bemerkenswert ist aber vor allem, dass in K eine elektrische Polarisation P gemessen wird, d.h. im Laborsystem K ist der Stab nicht nur magnetisiert, sondern auch elektrisch polarisiert. Diese Polarisation P spielt in allen Diskussionen eine wichtige Rolle. Sie ist der Grund für dieses elektrische Feld E im Magneten. Es soll untersucht werden, ob dieses Feld ein Wirbelfeld (rot E =/= 0) oder wirbelfrei (rot E = 0) ist. Im ersten Fall müssen die elektrischen Feldlinien nicht unbedingt geschlossen sein. E könnte auch eine Überlagerung eines wirbelfreien Felds mit einem reinen Wirbelfeld sein. Ruhende elektrische Ladungen sind typischerweise Quellen und Senken eines wirbelfreien elektrischen Feldes.

Im Einzelnen ergibt sich folgende Tabelle:

.

Nach der Überlegung (I) im Laborsystem entsteht aus dem Magnetfeld B' (gemessen im System des Stabs K') ein zusätzlicher Beitrag - v x B' zum elektrischen Feld E (gemessen in K). Dieses Feld wirkt auf im Stab ruhende Ladungen mit der Kraft F = - q v x B'. Das gilt lokal für jede Stelle, an der B' gemessen wird.

Aber: Weil im System K ein Magnetfeld B gemessen wird, entsteht in K eine zusätzliche Lorentz-Kraft F_L = q v x B auf die Leitungselektronen, die mit dem Stab mitbewegt sind, ein zunächst überraschender Gedanke. Beide Beiträge heben sich im Magneten (in guter Näherung, weil B ≈ B') gegenseitig auf. Das ist also der Fall, weil im Laborsystem nicht nur gewöhnliche Induktion, sondern zwei Effekte zu berücksichtigen sind: Ein relativistischer Effekt (F = - q v x B') und eine gewöhnliche Lorentz-Kraft (F_L = q v x B) .

Beide Effekte zusammen sorgen dafür, dass im Inneren des Magneten insgesamt keine Kraft auf eine Ladung wirkt. Der Schluss, dass dann auch keine Ringspannung und kein "Antrieb" für einen Ringstrom besteht, ist richtig, aber wie der Leser sehen wird, voreilig.

.

Das Argument ist nämlich noch nicht vollständig: Die Lorentz-Kraft ist auf den Bereich des magnetischen Stabs beschränkt. Wie verläuft aber das durch die Transformation entstandene Feld E außerhalb des Magneten? Liefert es außerhalb einen Beitrag zum Umlaufsintegral?

Man kann aber auch anders argumentieren: Im magnetisierten Stab ist  - vom BZS K der Leiterschleife aus - eine elektrische Polarisation P  zu messen, die in Abb. 1 nach vorn gerichtet,  wegen div P = - ρ bilden sich auf der Vorderfläche des Stabs positive Polarisationsladungen (gelb in die Zeichnung eingetragen) aus, auf der Gegenseite negative.

Die Folge von P ist ein elektrisches Feld E im Stab entgegengesetzt zu P (Im Inneren nach hinten; positive Ladungen vorn). Je nach Situation handelt sich um ein rein statisches elektrisches Feld oder es enthält als Anteil ein Wirbelfeld. Da dieses Feld mit den erwähnten Polarisationsladungen zusammenhängt, muss man erwarten, dass es nicht am Rand des Stabs, bei den positiven und negativen Polarisationsladungen plötzlich aufhört. Das wird später untersucht werden.

(Argument II) Wegen D = ε₀ E + P = 0  => E = - P/ε₀ = - v x M' / ε₀c² ≈ - v x µ₀ M = - v x B   gilt

E = - v x B    ,     da in B = µ₀ (H +  M)   H = 0.

E = - v x B  ist im Inneren des Stabs nach hinten gerichtet. Von der Leiterschleife aus ist dann eine Kraft auf frei bewegliche Ladungen im Magneten messbar:

F  = q E   = - q v x B (exakt - q v x B')

Das ist also wieder die elektrische Kraft auf frei bewegliche Ladungen im Magneten als Folge der elektrischen Polarisation, gemessen im BZS K.

Andererseits (Argument III): Im Magneten werden frei bewegliche Ladungen mitbewegt. Naiv könnte man glauben, dass sie "im Vergleich zu den mitbewegten Feldlinien" in Ruhe sind, also keine Lorentz-Kraft erfahren. Da es aber keine "Bewegung gegen Feldlinien" gibt (das Stachelmodell ist sicher falsch), auch keine "Bewegung gegen ein Feld" (nur eine "Bewegung gegen ein BZS, in dem ein bestimmtes Feld gemessen wird"), gibt es auch im System K der Leiterschleife mit seinem Magnetfeld B  ≈ B' eine Lorentz-Kraft auf freie Ladungen, die mit dem Magneten (Geschwindigkeit v) bewegt sind. Sie erfahren die Lorentz-Kraft  F_L = q v x B   ≈ q v x B' , weil sie sich in einem Magnetfeld B  ≈ B' bewegen (Im BZS K ist das tatsächlich eine magnetische Kraft, nicht etwa eine durch Lorentz-Transformation entstandene elektrische Kraft, wie F!).

Insgesamt ergibt sich wieder als Kraft auf frei bewegliche Ladungen im Magneten, vom Laborsystem K aus gesehen:          

F _total = F + F_L = 0    :

Beide Kräfte heben sich auf. Weder ein mit der elektrischen Polarisation P des Stabs zusammenhängendes elektrisches Feld E im Inneren des Magneten noch die Lorentz-Kraft können die Ursache für eine Induktion sein. Darauf weisen viele Autoren mit Recht hin.

.

Die Kräfte auf ein Leitungselektron im Magneten heben sich gegenseitig auf, auch gesehen vom Bezugsssystem des Magneten aus

Argumentation im System K' des Magneten:

Im System K' wird ein Magnetfeld B' gemessen. Es gibt keinen Grund für ein elektrisches Feld im Magneten. Relativ zu K' ruhen die mit dem Magneten mitbewegten Leitungselektronen: Es gibt auch keine Lorentz-Kraft auf Leitungselektronen im Stab - beurteilt vom BZS K' aus. Es gibt insgesamt keine Kraft auf Leitungselektronen im Magneten. Aber: Der U-förmige Rest der Leiterschleife bewegt sich im BZS K' mit der Geschwindigkeit -v. Auf Leitungselektronen in seinem Inneren wirkt eine Lorentz-Kraft -q v x B' (im BZS K' herrscht ja B' innerhalb des Magneten). Außerdem fällt am Rand des Magneten (immer noch im BZS K') die Flussdichte B' (abgesehen von Streufeldern) auf 0 ab. Der Rest der Leiterschleife bewegt sich also in einem inhomogenen Magnetfeld, unterschiedliche Anteile des magnetischen Flusses befinden sich innerhalb der Kurve C; es kommt nach der Flussregel zur Induktion. Ohne dass dies jetzt hier quantitiv ausgeführt wird, ist plausibel, dass sich auch von diesem BZS aus zwei Effekte - Induktion und Lorentz-Kraft - gegenseitig in ihrer Wirkung aufheben. Deshalb kann auch - gesehen vom System K' - kein Ringstrom zustandekommen.

Die Flussregel (beruhend auf der Kurve C) allein ist hier nicht anwendbar, weil zwei Effekte zusammenwirken: im BZS K elektrische Polarisation des Stabs und Induktion (über die Lorentz-Kraft) bzw. im BZS K' gewöhnliche Induktion und Lorentz-Kraft.

.

Also, das Argument ist immer noch nicht vollständig: Für die Ringspannung (berechnet im BZS K) sind ebenfalls zwei Beiträge^*) zu berücksichtigen: U₀ = W/q = W_el/q + W_mag/q =   ∫₀ E·ds +   ∫₀ F_L·ds /q , jeweils berechnet für einen vollständigen Umlauf längs der Kurve C. Zum ersten Umlaufsintegral kann nur ein elektrisches Wirbelfeld beitragen, ein eventuell vorhandenes wirbelfreies Feld würde herausfallen. Das zweite Umlaufsintegral ist sicher von 0 verschieden, weil die Lorentz-Kraft auf den Bereich des Magneten beschränkt ist.

Wie verläuft das durch die Transformation bzw. Polarisation entstandene elektrische Feld außerhalb des Magneten? Liefert es einen Beitrag zum Umlaufsintegral?

Wäre das elektrische Feld als Folge der Polarisation ein wirbelfreies Feld, wie man es auf Grund seiner Quellen in den Polarisationsladungen vermuten könnte, würde das Umlaufsintegral verschwinden. Dann würde die Lorentz-Kraft unkompensiert überleben und zu einer Ringspannung beitragen. Andernfalls müsste man sowohl das nicht verschwindende Umlaufsintegral über die elektrische Feldstärke wie die Lorentz-Kraft in Rechnung setzen mit der Chance der vollständigen Kompensation.

.

Richtige Interpretation der Flussregel für diesen Fall

Bei einem in x-Richtung endlich langen magnetisierten Stab gibt es also keine Induktionsspannung. Das frühere Argument im Zusammenhang mit Abb. 1 bzgl. der grün markierten angeblichen Flussänderung muss also falsch sein. Gemäß eines anderen Artikels sollte man aber zur Analyse der zugehörigen Fläche eine "materiell mitbewegte Kurve" (z.B. C') heranziehen (siehe Abb. 4). Sie umfährt den grün markierten Bereich zwischen den beiden Kontaktspitzen. Der Leser erkennt, dass es hier keine Änderung des magnetischen Flusses innerhalb der geschlossenen Leiterschleife gibt, also wiederum keine Induktionsspannung. So wird auch bei üblichen Deutungen des Hering'schen Paradoxons argumentiert.

.

Untersuchung des in Bewegungsrichtung unendlich langen Magneten

In der Literatur wird oft gezeigt, dass dieses Feld E ein rein elektrostatisches (wirbelfreies) Feld ist, wenn der Stab in x-Richtung beliebig lang ist. In vielen Fällen, so auch hier, wird tatsächlich ein Unipolarinduktionsstrom, und damit eine Ringspannung, beobachtet. Woher kommt sie?

Wir überlegen uns den Sachverhalt zunächst noch für einen in x-Richtung endlich langen Stab im BZS K. Dann sollten die bisherigen Überlegungen bestätigt werden. Wo sind im System des Leiterrings Wirbel des elektrischen Feldes zu erwarten? Nun, rein anschaulich da, wo sich das elektrische Feld E in seine Querrichtung ändert. Das ist an den Rändern bzw. Seitenflächen des Stabs der Fall. Später vollziehen wir den Grenzübergang zu einem in x-Richtung unendlich langen Stab.

Eine Queränderung ist auffällig, wenn es sich nicht um einen in y-Richtung unendlich langen Stab handelt. Dann gibt es zusätzlich zu dem Magnetfeld in y-Richtung innerhalb des Stabs wegen div B = 0 ein Rückfeld, das die Leiterschleife z.T. ebenfalls senkrecht, überwiegend in negative y-Richtung durchsetzt. Bei einem (in y-Richtung) unendlich langen Stab dagegen ist dieses Rückfeld vernachlässigbar. Der Stab soll hier so lang sein, dass dies auch näherungsweise noch gilt. Andernfalls würde dieses Rückfeld die folgenden Überlegungen zum Teil verfälschen.

Führen wir wieder eine stetige Magnetfeldverteilung für den Stab ein. Wir argumentieren im Laborsystem K. In positive x-Richtung gehend soll also das Magnetfeld am linken Rand von 0 auf den positiven Wert B in y-Richtung wachsen und am rechten Rand von B wieder auf 0 fallen. Statt des allmählichen Übergangs gehen wir gleich zum Grenzfall über, d.h. eine sprunghafte Änderung, beschrieben durch die Theta-Funktion. Die Geschwindigkeit v kann dann für den ganzen Magneten als konstant angesehen werden. Dann gilt für die Bewegungsrichtung im Bezugssystem der Leiterschleife für - der Einfachheit halber einen quaderförmigen Magneten:

B = B(x,y,z) j = B j [ Θ(x - v·t) - Θ(x - l_x - v·t) ] [ Θ(z) - Θ(z - l_z) ]

mit

∂B/∂x = B · [ δ( x - v·t) - δ( x - l_x - v·t)] [ Θ(z) - Θ(z - l_z) ]

Θ(x) ist die Theta- oder Sprung-Funktion , δ(x) ihre Ableitung, die Delta-Funktion. In y-Richtung kann das B-Feld sicher nicht schlagartig aufhören. Dort ist ein Θ-Ansatz sicher nicht sinnvoll. Dass B hier im Ansatz unbeschränkt in y-Richtung fortgesetzt wird, ist eine Näherung; sie spielt aber keine Rolle.

Dann gilt für das elektrische Feld E = - v x B nach I (relativistischer Effekt):

rot E = -rot (v x B) = - v(div B) + B (div v) - (B·grad) v + (v·grad) B

=  B (div v) -  (B·grad) v + (v·grad) B            ,           da wegen div B = 0 das B-Feld quellfrei ist, also nur "geschlossene Feldlinien" besitzt.

=  (v·grad) B ,  da v = konstant,

also

rot E =   v ∂B/∂x j  

Die einzigen Beiträge zu rot E sind in B-Richtung (y-Richtung) oder entgegengesetzt dazu orientiert, und zwar an solchen Stellen in Bewegungsrichtung, wo sich das B-Feld ändert. Dieses elektrische Wirbelfeld E hat im Inneren des Magneten - vom Laborsystem aus beurteilt - die diskutierte negative z-Richtung. Es wird aber in der Regel nicht außerhalb des Magneten plötzlich aufhören. Generell kann man das E-Feld im ganzen Raum im Prinzip berechnen aus seinen Quellen (div E = - div P/ε₀) und seinen Wirbeln (rot E = v ∂B/∂x  j), wie in jedem Lehrbuch der Elektrodynamik nachzulesen ist. Es geht aber einfacher:

Wir berechnen gleich das Umlaufsintegral. Wählt man eine geschlossene Kurve längs der Leiter, die in Richtung des E-Felds durchlaufen wird, so muss der zugehörige Flächenvektor df in negative y-Richtung orientiert sein (df = - dx·dz j). Nach dem Stokesschen Satz kann zum Umlaufsintegral nur die Komponente von rot E in y-Richtung beitragen. Anteile in x-Richtung, die bei anderen Näherungen an der oberen oder unteren Begrenzungsfläche in y-Richtung entstehen könnten, spielen offenbar keine Rolle.

Es ergibt sich also für das Umlaufsintegral (die Ringspannung) längs der Leiterschleife im Laborsystem (bei einem in x-Richtung endlich langen Magneten in Positionen entsprechend Abb. 1):

 ∫₀ E(r) · dr = ∫₀ rot E · df = = - ∫₀ (  v · B · [ δ( x - v·t) - δ( x - l_x - v·t)] [ Θ(z) - Θ(z - l_z) ]  dx·dz )

=  B· v· l_z

Nur die zweite δ-Funktion (mit dem negativen Vorzeichen: δ( x - l_x - v·t)) konnte einen Beitrag liefern, wenn die geschlossene Kurve irgendwo zwischen der linken und der rechten Seitenfläche den Magneten durchstieß. Die Integration über die Θ-Funktionen in z-Richtung ergab den Faktor l_z.)

.

Beiträge zur Ringspannung längs einer beliebigen geschlossen Kurve C: Insgesamt 0 bei einem endlich langen Magneten

Aus dem elektrischen Wirbelfeld ergibt sich auch hier der übliche Ausdruck nach der naiven Herleitung mit der Flussregel. Für die Ringspannung ist noch der Beitrag zur Verschiebungsarbeit von der Lorentz-Kraft her (mit gleichem Betrag) zu berücksichtigen: Insgesamt ist die Verschiebungsarbeit für einen geschlossenen Weg 0: keine Ringspannung und kein Ringstrom.

.

Die Rolle des Wirbelfelds wird von manchen Autoren übersehen. Andere Autoren erkennen den Beitrag  (v·grad) B =/=0, wenn der Stab in x-Richtung nur endlich ausgedehnt ist. Sie leugnen dann mit Recht die Entstehung des Wirbelfelds bei unendlicher Ausdehnung des Magneten in x-Richtung.

.

Unendlich langer Magnet: keine Änderung des magnetischen Flusses und kein Beitrag zur Ringspannung vom elektrischen Feld her

Einziger Beitrag zur Ringspannung als Folge der Lorentz-Kraft: Unipolarinduktion

Bei unendlicher Ausdehnung des Magneten in x-Richtung gibt es keinen Beitrag zum Integral von den Delta-Funktionen her; niemals wird eine der Stirnflächen des Magneten von der Leiterschleife umfasst. Die Wirbel von E liegen dann auch außerhalb jeder endlichen geschlossenen Kurve C, z.B. der Leiterschleife. Das ist auch anschaulich klar, weil sich dann der magnetische Fluss innerhalb der Leiterschleife nie ändert. Das durch die Polarisation des Magneten entstandene elektrische Feld existiert auch hier, aber für ein wirbelfreies Feld verschwindet das Umlaufsintegral. Ein Beitrag zur Ringspannung kann in diesem Fall wie im eingangs erwähnten Beispiel der bewegten Leiterbrücke nur durch die Lorentz-Kraft kommen. Dieser überlebt. Folge dieser Ringspannung ist ein Ringstrom: eine Unipolar-Induktions-Maschine bei in x-Richtung unendlich ausgedehntem Magneten. In der Flussregel sind in diesem Fall beide Seiten 0. Sie trägt jetzt nichts zum Verständnis der Induktion bei. Die Kompensation der Kräfte im Magneten findet auch hier statt. Der Leser erkennt die Bedeutung der vorhandenen oder nicht vorhandenen Randwirbel von E und des elektrischen Feldes, das außerhalb des Magneten die Fortsetzung des elektrischen Feldes im Magneten bildet.

Nun ist diese Situation aber geometrisch kaum vorstellbar. Eine etwas geänderte Anordnung lässt sich aber in weitgehend gleicher Weise analysieren.

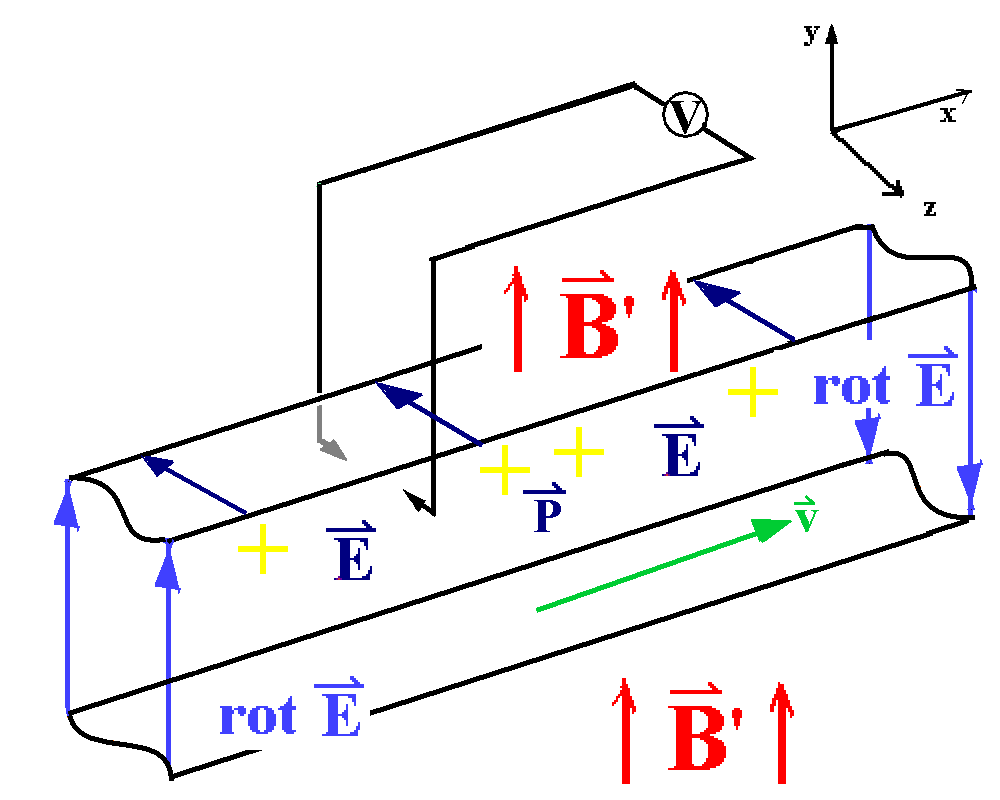Abb. 2: Modifizierte Anordnung: Ein in x-Richtung unendlich langer quaderförmiger magnetisierter Stab ("Magnet"; Ursache von B) bewege sich im Laborsystem , in dem die Leiterschleife ruht, gleichförmig mit v in x-Richtung. Mittels Kontakten gleiten die Leiterenden auf dem gut leitenden Magneten. Die Wirbel von E bzw. die Stellen, wo sich B ändert, liegen immer außerhalb der Leiterschleife, tragen also zur Ringspannung nicht bei. Auch das elektrische Feld E (Folge der Polarisation) nicht, da es hier ein wirbelfreies Feld ist. Die beobachtete Unipolarinduktion ist hier eine Folge der Lorentz-Kraft.

Hinweis:

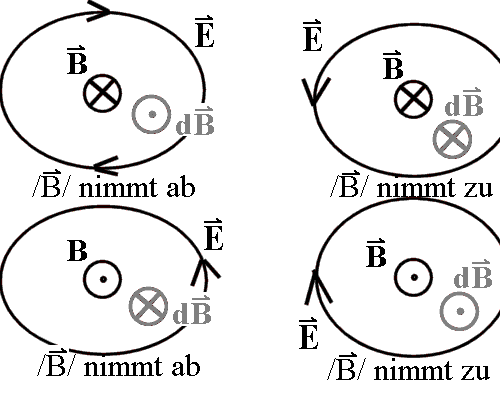Zur Richtungsentscheidung: ∂B/∂x ist am linken Rand in positive B-Richtung (also positive y-Richtung), der zugehörige Beitrag zu rot E ist also in y-Richtung orientiert. Ganz entsprechend ist ∂B/∂x  am  rechten Rand negativ, der zugehörige Beitrag zu rot E ist also in -y-Richtung orientiert. Es ergeben sich die blauen Pfeile der Abb. 1 und damit die Richtung des induzieren E-Feldes nach der Rechten-Hand-Regel. Wieder sieht man, dass sich das entstehende Wirbelfeld an den Rändern des magnetischen Stabs ergibt, wobei es aber ausschließlich auf die Wirbelkomponenten in y-Richtung ankommt. Ein anschauliches Argument für die Richtungsentscheidung ist folgendes:  Für einen Beobachter im Laborsystem (relativ zu dem sich der Stab bewegt), kann die Veränderung des Magnetfelds infolge der Bewegung auch durch zeitliche Veränderung gedeutet werden. In Bewegungsrichtung hinter dem Stab verschwindet das Magnetfeld B durch ein Zusatzfeld dB in negative y-Richtung, davor wächst es durch ein Zusatzfeld dB in positive y-Richtung. Wegen rot E = - ∂B/∂t müssen also links Wirbel mit rot E in positive y-Richtung, rechts in negative y-Richtung entstehen, wie es auch die formale Rechnung zeigt (Abb. 3)

Abb. 3: Anschauliche Regel zur Richtungsentscheidung: dB kennzeichnet jeweils eine zeitliche Änderung der magnetischen Flussdichte durch ein fiktives Zusatzfeld. Wegen rot E = - ∂B/∂t ist rot E jeweils entgegengesetzt zu dB. Nach der rechten Handregel entsteht das elektrische Wirbelfeld mit dem eingezeichneten Durchlaufssinn.

.

.

Zusammenfassung

Damit ist klar:

Bei endlicher Ausdehnung des Magneten in x-Richtung entsteht zwar - wie bei allen Induktionsvorgängen in einem geeigneten Bezugssystem - ein elektrisches Wirbelfeld entsprechend der Flussregel. Aber es entsteht keine Ringspannung und damit auch kein Ringstrom. Grund für die ausbleibende Induktion ist, dass sich hier zwei Effekte - vom BZS der ruhenden Leiterschleife aus gesehen - gegenseitig aufheben: (1) die elektrische Polarisation P des bewegten Magneten, ein relativistischer Effekt (für sich genommen könnte sie bei endlicher Ausdehnung in x-Richtung ein elektrisches Wirbelfeld E zur Folge haben.) (2) die Lorentz-Kraft auf mit dem Magneten mitbewegte Leitungselektronen. In dieser Betrachtungsweise ist weder die Lorentz-Kraft noch die Kraft des elektrischen Felds im Inneren des bewegten Magneten die treibende Kraft, weil sich beide vollständig aufheben. (Beide sind überdies auf den Bereich des Magneten beschränkt. Dieses Argument reicht aber zur Begründung noch nicht aus.) Andererseits tragen auch das elektrische Wirbelfeld infolge der Polarisation und die Lorentz-Kraft mit gleichen Beträgen zur Ringspannung bei, die sich gegenseitig aufheben. (Das endlich ist der Grund!) Bei unendlicher Ausdehnung des Magneten in x-Richtung arbeitet die Anordnung als (idealisierte) Unipolar-Induktionsmaschine. Es entsteht kein elektrisches Wirbelfeld (auch keine Änderung des magnetischen Flusses) im Laborsystem, aber als Folge der Lorentz-Kraft eine von 0 verschiedene Ringspannung und ein Ringstrom. (Trotzdem heben sich im Inneren des Magneten eine elektrische Kraft und die Lorentz-Kraft gegenseitig auf.) Zur Analyse reichte es nicht aus, die Kräfte auf Leitungselektronen im Magneten zu betrachten. Es musste noch untersucht werden, ob ein elektrisches Wirbelfeld vorhanden ist, das auch einen Beitrag zur Ringspannung leisten kann. Dadurch unterscheiden sich die Situationen bei einem in Bewegungsrichtung endlich langen und unendlich langen Magneten.

Zur Problematik des "mitbewegten" BZS bzw. der vielen mitbewegten BZS siehe Induktion.pdf.

.

Vergleich unterschiedlicher Betrachtungsweisen

Hier wird tabellarisch noch einmal zusammengestellt, wie sich Argumentationen zur Induktion in unterschiedlichen BZS unterscheiden, wie sie aber dennoch zum gleichen Ergebnis führen.

.	Labor-System (E)	Labor-System (U)	"mitbewegte" BZS (E)	"mitbewegte" BZS (U)
im Magnetfeld bewegter Leiterstab	kein elektrisches Wirbelfeld	Ringspannung und Ringstrom durch Lorentz-Kraft	elektrisches Wirbelfeld	keine Lorentz-Kraft; Ringspannung und Ringstrom durch elektr. Wirbelfeld
bewegter Magnet (endlich lang in x-Richtung)	Elektrisches Feld infolge der Polarisation des bewegten Magneten. Es besitzt Wirbel an den Stirnseiten des Magneten.	Wirkung von elektrischem Feld und Lorentz-Kraft im Magnetfeld B' heben sich im Inneren des Magneten auf; jedoch ebenso die Beiträge zur Ringspannung infolge des Wirbelanteils von E und infolge der Lorentz-Kraft (ein wirbelfreier Anteil von E fällt bei der Ringspannung ohnehin heraus) => keine Ringspannung	Leitungselektronen ruhen in einem konstanten Magnetfeld; auch kein statisches elektrisches Feld als Folge einer Polarisation. Aber Induktion, weil B' am Rand des Magneten auf 0 abfällt.	Lorentz-Kraft auf Ladungen im U-förmigen Leiterbügel, der mit -v im Magnetfeld B bewegt ist. Beide Beiträge zur Ringspannung heben sich gegenseitig auf. => keine Ringspannung
bewegter Magnet (unendlich lang in x-Richtung)	keine Flussänderung innerhalb der Leiterschleife und kein elektrisches Wirbelfeld. Das elektrische Feld infolge der elektrischen Polarisation des Magneten ist wirbelfrei.	Ringspannung allein durch die Lorentz-Kraft auf Ladungen im Magneten, weil ein wirbelfreies elektrisches Feld zur Ringspannung nichts beitragen kann. (trotzdem heben sich die Kräfte durch das wirbelfreie elektrische Feld und durch die Lorentz-Kraft im Inneren des Magneten gegenseitig auf) => Ringspannung und Ringstrom	keine gewöhnliche Induktion, weil sich B' nirgendwo innerhalb der Leiterschleife ändert.	Lorentz-Kraft wie oben. => Ringspannung und Ringstrom

.

Mit den hier untersuchten Problemen bei einem in x-Richtung endlich langen Magneten hängt sehr eng das Hering'sche Paradoxon zusammen. Als Paradoxon wird es wegen folgender fehlerhafter Argumentation bezeichnet: Bei Bewegung des Permanentmagneten zwischen den Kontakten (oder der Bewegung der Kontakte) ändere sich danach der magnetische Fluss. Obwohl die Flussregel ein elektrisches Wirbelfeld voraussage, entsteht keine Ringspannung. Dazu ist zu sagen:

(1) Nach den Überlegungen oben überlagern sich hier zwei Effekte, nämlich die Induktion (beschrieben durch die Änderungsrate des magnetischen Flusses, bzw. durch einen relativistischen Effekt, nämlich die elektrische Polarisation infolge der Magnetisierung) und die Lorentz-Kraft. Beide Effekte heben sich gegenseitig auf.

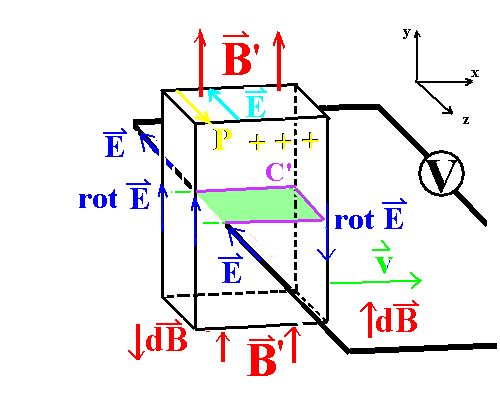(2) Will man den relativistischen Effekt ausschließen, sollte man die Kurve C, längs der die Ringspannung untersucht wird, nicht durch einen Bereich legen, in dem eine elektrische Polarisation auftritt. Die geschlossenen Kurven C können dann nicht durch den magnetisierten Körper verlaufen (z.B. die Kurve C' nach Abb. 4). Dann kommt es auch nicht zu einer Änderung des magnetischen Flusses, also wieder keine Induktion (vgl. Kap. V zum Hering'schen Paradoxon von Induktion.pdf. Anregung zu dem Argument habe ich gefunden in der dort zitierten Literaturstelle [11]). Man kann Schwierigkeiten vermeiden, wenn man sich bei der Anwendung der Flussregel heuristisch auf "körperlich mitbewegte Kurven", wie C, beschränkt (siehe erwähnte PDF-Datei). C' umfährt so, violett gezeichnet, den in Abb. 4 grün markierten Bereich zwischen den beiden Kontaktspitzen. Der Leser erkennt, dass es hier innerhalb der Leiterschleife keine Änderung des magnetischen Flusses gibt, also wiederum keine Induktionsspannung. So wird auch bei üblichen Deutungen des Hering'schen Paradoxons argumentiert.

Abb. 4: Geeignete Wahl der Kurve C' entsprechend der Flussregel. Der magnetische Fluss (z.T. grün markiert) wird so aus der Leiterschleife ausgeschlossen: keine Flussänderung und keine Induktion bei in x-Richtung endlichem Magnetstab.

(3) Wie hier gezeigt wurde, kommt es bei einem in x-Richtung unendlichen magnetisierten Stab zu keinem elektrischen Wirbelfeld (die elektrische Polarisation erzeugt ein wirbelfreies elektrisches Feld), sehr wohl aber zu einer Ringspannung infolge der Lorentz-Kraft und damit zur Induktion. Die Lorentz-Kraft führt zu einer Ringspannung, weil sie auf den Bereich des Magneten beschränkt ist. Es handelt sich dann um eine Unipolar-Induktionsmaschine.

.

Literatur

[1] Panofsky, W. und Phillips, M. , Classical Electricity and Magnetism, Addison Wesley Publishing Company, Reading, Palo Alto, London, 2. Auflage 1964, S. 158 ff, S. 336 ff

[2] Becker, R., Sauter, F., Theorie der Elektrizität, Teubner Verlagsgesellschaft, Stuttgart, 18. Auflage 1964, S. 119 ff u. S. 264 ff

[3] Grabinski H., Der Heringsche Versuch: Mythen und Fakten, Electrical Engineering, Archiv für Elektrotechnik, 80, S. 285 - 290, 1997, S. Auch                                http://www.lfi.uni-hannover.de/text/germ/people/Grabinski/htmls/abstr9.html

[4] Giuliani, G., On electromagnetic induction:         http://fisicavolta.unipv.it/percorsi/pdf/emi_web.pdf  (hierbei u.a. "Kaempffer's example")

.

^*) Die Definition der Ringspannung U₀ als W/q für einen geschlossenen Weg ist bei Vorliegen allein eines elektrischen Wirbelfelds kompatibel mit der DIN-Norm. Für den Fall, dass für den geschlossenen Weg auch noch eine andere Arbeit (z.B. eine magnetische durch die Lorentz-Kraft) verrichtet wird, ist es naheliegend, diese ebenfalls mit einzubeziehen: U₀ = W/q = W_el/q + W_mag/q . Das wird bestätigt durch die Betrachtung des gleichen Vorgangs aus verschiedenen Bezugssystemen, wo sich die gleiche Ringspannung ergeben sollte. Ohne eine Ringspannung kann es - außer im Supraleiter - keinen Ringstrom geben!

.

(zuletzt aktualisiert und ergänzt Februar 2014)

.

.

.