Startseite Didaktogene Lernschwierig- keiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis    Schüler- versuche Physik Lernen mit dem Computer  Meta- Physikalisches  Begriffliches Experiment des Monats Physik für Schülerinnen und Schüler Impressum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2011

Das Flugzeug im Magnetfeld - ein Paradebeispiel für die Induktion?

Der Aufsatz richtet sich an Lehrer, nicht an Schüler.

Hier wird eine Standardaufgabe aus der Schulphysik untersucht: Ein Flugzeug "schneidet mit seinen Flügeln senkrecht die Magnetfeldlinien".

Fragestellung:

a) Wie laden sich die Flügelspitzen auf?

b) Welche Spannung ist zwischen den Flügelspitzen zu messen?

c) Hat das Problem etwas mit Induktion zu tun? Gibt es eine Ringspannung, wie sie das Induktionsgesetz fordert?

Die Aufgabe ist nur scheinbar trivial. Der Leser kann durch die genaue Analyse eine ganze Menge über Induktion lernen.

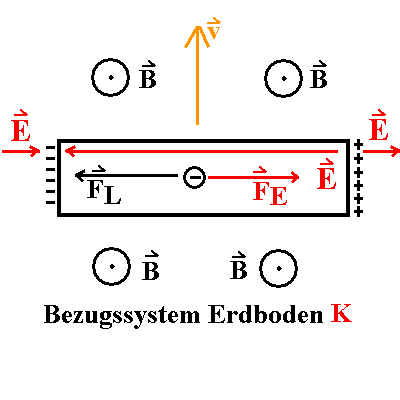Abb. 1: Situation für den im Magnetfeld bewegten leitenden Stab (Flügel, Leiterbrücke), gesehen vom Erdsystem K (Tower) aus, wenn er isoliert ist.

1. Bezugssystem Erdboden/Tower K: Vom Tower aus sieht die Situation so aus: Wir betrachten das elektrisch isolierte Flugzeug. Im BZS K gibt es ein magnetisches Feld B. Mit den Flügeln des Flugzeug werden Elektronen mitgerissen, Geschwindigkeit v in Bewegungsrichtung des Flugzeugs. Es folgt eine Lorentzkraft zu einer der Flügelspitzen hin. Elektronen im Metall der Flugzeughülle werden in ihre Richtung gezogen. Die in Flugrichtung linke Flügelspitze lädt sich negativ auf, die andere positiv. Dadurch entsteht ein (statisches) elektrisches Feld E, bis sich Lorentzkraft und elektrische Kraft gegenseitig aufheben. Dann ist die Ladungsverschiebung beendet. Dieses Feld E im Inneren des Stabs muss wegen des Kräftegleichgewichts homogen sein und entspricht damit dem idealen Feld eines Plattenkondensators. Im Erdsystem K könnte die Aufladung der Flügelspitzen durch eine elektrische Spannung U = E·ℓ gemessen werden, wenn ℓ die Spannweite der Flügel ist. Dabei wollen wir uns jetzt nicht um das Vorzeichen der Spannung kümmern. Allerdings ist das beim Flugzeug technisch unmöglich, weil die Flügelspitzen nicht auf Drähten gleiten. So wird man im Erdsystem K die Überlegung nicht überprüfen können. Dieselben Überlegungen gelten aber auch für einen beliebigen im Magnetfeld bewegten Stab, bei dem eine solche Messung realisiert werden kann. Nutzen wir das Kräftegleichgewicht (KGG) zwischen der Lorentz-Kraft und der sekundären elektrischen Kraft:     q· v x B = - q·E  (q sei die Ladung eines Leitungselektrons; beide Kräfte nur dem Betrag nach gleich; entgegengesetzt), also  E = - v x B, gleichgerichtet mit der Lorentzkraft im Inneren des Stabs. Das ist das sekundäre elektrische Feld, das sich als Folge der Ladungstrennung ausbildet. Zwischen den Flügelspitzen bildet sich also die Spannung U = E· ℓ  = B· v· ℓ aus. Hier muss die übliche schulisches Argumentation enden. Meist wird in der Schule kommentarlos angenommen, dass dieselbe Spannung auch bei Stromfluss vorhanden ist, oder sogar die Ursache für diesen Stromfluss ist. Wie weit ist die Annahme gerechtfertigt?

Dabei ist klar:

1. Wenn die Enden des Stabs (die Flügelspitzen) im Erdsystem mit sehr gut leitenden Verbindungen versehen wären, könnte sich das Feld E und die damit zusammenhängende statische Spannung nicht ausbilden. Dennoch würde ein Strom fließen, veranlasst durch die Lorentz-Kraft.

2. Es ist außerdem bekannt, dass ein Potenzialfeld (wie etwa in einem Kondensator) nicht für einen stationären Strom sorgen kann. Es kann nicht die Energie herbeischaffen, die zum Ausgleich von Verlusten nötig wäre. Dieses sekundäre Feld E ist nur ein Vehikel, um die Größe der Lorentz-Kraft zu ermitteln. Für einen Induktionsstrom spielt es keine Rolle.

3. Das sieht man auch daran: Wäre dieses Feld E (diese Spannung U) in einem geschlossenen Stromkreis vorhanden, würde es zum Teil die Leitungselektronen antreiben (außerhalb der Flügel oder der Leiterbrücke), zum Teil behindern (innerhalb der Flügel). Das letzte war ja gerade der Grund, weshalb sich ein Kräftegleichgewicht in der Leiterbrücke einstellte. Trotz des richtigen Betrags ist die obige statische Spannung, die auch in den Schulbüchern üblicherweise hergeleitet wird, als Induktionsspannung, die einen Ringstrom antreibt, ungeeignet. Als Herleitung der Hall-Spannung ist die Argumentation akzeptabel.

Gibt es  dagegen hier eine Ringspannung, mit der üblicherweise das integrale Induktionsgesetz (die "Flussregel") formuliert wird? Natürlich gibt es keine geschlossene Kurve, die ganz im Erdsystem ruht und trotzdem die Flügel / die Leiterbrücke enthält.

Fall 1:

Wählt man eine beliebige geschlossene Kurve, von der der einzige leitfähige Teil aus den Flügeln (dem Stab) besteht, und wovon der Rest der Kurve im Erdsystem K ruht, kann das elektrische Feld E nichts zum Umlaufsintegral über das elektrische Feld beitragen, weil sich Beiträge - wie bei jedem Potenzialfeld - gegenseitig aufheben. Wenn wir aber von der allgemeineren Definition der Spannung ausgehen: Arbeit pro Ladungsmenge, müssen wir im Erdsystem K auch die magnetische Lorentz-Kraft berücksichtigen. Sie liefert dann einen nichtverschwindenden Beitrag zur Ringspannung (siehe unten).

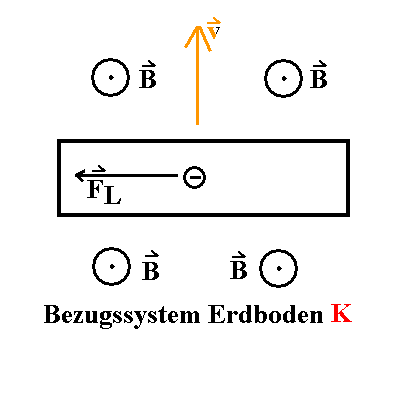Abb. 2: Gleiche Situation, wenn die Enden des Stabs durch einen guten Leiter verbunden sind. Wir stellen uns vor, dass sie mit gutem Kontakt auf einem U-förmigen Leiter gleiten. Dann kann sich das statische elektrische Feld E nicht ausbilden.

Fall 2: Betrachten wir einen anderen Extremfall: Wenn die Flügelspitzen mit gutem Kontakt auf gut leitenden Drähten im Erdsystem K gleiten, kann sich das sekundäre Feld E nicht aufbauen. Es entsteht ein Ringstrom. Gibt es hier ein elektrisches (Wirbel-)Feld? Die Antwort wird in dieser geschlossenen Kurve sein: Nein! Aber es gibt eine Ringspannung! 2 Fälle sind zu unterscheiden: a) kein Widerstand im Stromkreis (unendliche Leitfähigkeit): supraleitender Sonderfall. Hier ist der Strom durch die London-Gleichung begrenzt. Darauf soll hier nicht eingegangen werden. b) Ein Widerstand ist im Stromkreis  vorhanden. Dann ist Arbeit nötig um den Strom fließen zu lassen. U.U. entsteht auch ein Spannungsabfall im Außenleiter zwischen den Flügelenden, also auch eine Ringspannung. Wir wählen die Situation endlicher, aber sehr großer Leitfähigkeit. Dann entsteht in guter Näherung noch kein sekundäres Feld E im Inneren und außerhalb der Flügel, aber der Fall a) braucht nicht beachtet werden. Falls ein solches Feld E vernachlässigbar ist: Die Arbeit  zur Verschiebung einer Ladung q bei einem Umlauf ist - ∫ 0  F·ds  (das soll ein Umlaufintegral über einen geschlossenen Weg sein; F ist die Kraft des Feldes auf q). In diesem Fall kann nur der Weg (der Länge ℓ) über das Flugzeug selbst zum Integral beitragen, denn nur dort ist die Kraft von 0 verschieden (die Lorentz-Kraft). Also gilt für die Arbeit - ∫ 0  F·ds  =  - q· v· B·ℓ. Da Spannung (auch in der Form der Ringspannung) als Arbeit pro Ladungsmenge (DIN 1324) definiert ist (und nur im Spezialfall der Elektrostatik als Potenzialdifferenz), gilt für den Betrag der Ringspannung U = B· v·ℓ , mit dem gleichen Betrag wie auch elementar hergeleitet. Man erkennt, dass auch in diesem Fall die Ringspannung durch kein elektrisches Feld zustande kommt, sondern eine Folge der magnetischen Lorentz-Kraft ist.

Fall 3:

Damit können wir das Ergebnis verallgemeinern. Bei der Ringspannung fällt ein Potenzialfeld E, wie groß auch immer es sei, völlig heraus. Per definitionem sind Potenzialdifferenzen wegunabhängig; andernfalls besäße das Feld E kein Potenzial. Einziger Beitrag zur Ringspannung kommt von der magnetischen Lorentzkraft! Wir können die Berechnung von E, wie sie in der Schule üblich ist, als einen Trick auffassen, die Ringspannung in eine gleichgroße statische Spannung (also Potenzialdifferenz) umzuwandeln, die leicht berechnet und im Prinzip gemessen werden kann. Mit der Induktion selbst hat diese sekundäre Spannung offenbar wenig zu tun. Sie ist nicht Ursache des Induktionsstroms.

Ein genügend empfindlicher elektrostatischer Spannungsmesser könnte - im Fall fehlenden Stroms, aber über Drähte, im BZS K in Verbindung mit den Flügelspitzen - im Prinzip - die Spannung im Außenkreis zwischen den Flügelspitzen messen. Man kann die Meinung vertreten, dass dies dann die Spannung wäre, die mit dem sekundären elektrischen Feld zusammenhängt, das sich durch die Ladungsverschiebung ausbildet. Dieses elektrische Feld  ist dann also ein sekundäres statisches (Potenzial-)Feld, an dem die - anders definierte - Ringspannung abgelesen werden kann. Sie entspricht der Hall-Spannung.

Warum wird jetzt im Flugzeug keine Spannung nachgewiesen? Um das zu entscheiden wäre es eigentlich naheliegend, in das mitbewegte BZS K' übergehen.

Ein Spannungsmesser setzt in jedem Fall voraus (also auch ein elektrostatisches Voltmeter), dass durch Ladungen Kräfte entstehen. Im Fall ohne Stromfluss gibt es im Inneren des Flugzeugs - gesehen vom System K aus - keine resultierende Kraft auf Ladungen. Ein mitfliegender Spannungsmesser im Inneren kann nicht ausschlagen.

Der Tower antwortet also: Man kann sich überlegen, dass sich der linke Flügel in Abb. 1 negativ auflädt. Aber weder die Ladung noch die Spannung können wir von uns aus (System K) experimentell nachweisen, teils aus technischen Gründen, weil die Flügel nicht auf Drähten gleiten, teils prinzipiell, weil das Innere des Flugzeugs kräftefrei ist.

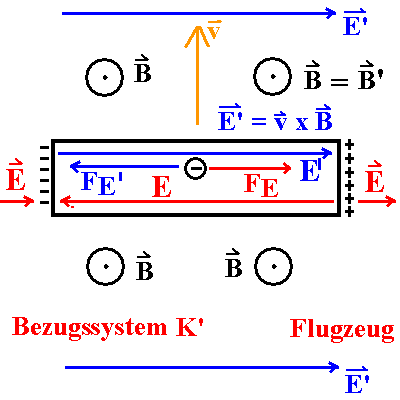Abb. 3: Der isolierte leitende Stab in seinem Ruhesystem (im Bezugssystem des Flugzeugs K')

2. Mitbewegtes  Bezugssystem Flugzeug K': Naheliegender wäre es, die Situation von einem Flugpassagier betrachten zu lassen. Sie sieht ganz anders aus (Abb. 3): Im BZS K' wird ein magnetisches Feld B' = B (in nichtrelativistischer Näherung) gemessen, aber alle Ladungen im Flugzeug ruhen in diesem Magnetfeld. Es gibt also keine Lorentzkraft. Es ist ja nicht so, wie manchmal suggeriert wird, dass man durch das "Schneiden der Feldlinien" eine Bewegung gegenüber dem Magnetfeld beobachten könnte. Bei der Bewegung wird vielmehr immer das gleiche Magnetfeld B' gemessen. An B' ist eine Relativbewegung nicht erkennbar. Aber gemäß der Relativitäts-Theorie gibt es in diesem BZS K' ein durch Lorentz-Transformation entstandenes elektrisches Feld E' = v x B (in nichtrelativistischer Näherung, blau gezeichnet). BZS K' bewegt sich mit der Geschwindigkeit v gegenüber dem System K, in dem das Magnetfeld B gemessen wird). Wenn B homogen ist, ist auch E' überall im BZS K' homogen. Innerhalb der Flügel verschiebt es durch die elektrische Kraft FE' Elektronen in seine Gegenrichtung, also in der Zeichnung ebenfalls nach links. Die isolierten Flügelspitzen laden sich auf. In den Flügeln und außerhalb entsteht dadurch ein sekundäres elektrisches Feld E (rot gezeichnet) bis sich die beiden elektrischen Kräfte FE' und FE gegenseitig aufheben. Dann ist die Ladungsverschiebung beendet. a) Das Innere des Flugzeugs ist dann frei von elektrischem Feld. Eine Lorentzkraft existiert auch nicht. Im Flugzeug kann also die Aufladung nicht durch eine Spannung gemessen werden. Ein Spannungsmesser im Flugzeug-Inneren schlägt nicht aus. b) Wählt man eine beliebige geschlossene Kurve, von der die Flügel (den Stab) den einzigen  leitfähigen Teil  bilden, und die ganz im Bezugssystem K' ruht, so kann ebenfalls keine Spannung gemessen werden, aus zwei Gründen:   1. Das sekundäre elektrische Feld E kann nichts zum Umlaufsintegral über das elektrische Feld beitragen, weil sich Beiträge - wie bei jedem Potenzialfeld - gegenseitig aufheben. 2. Die geschlossene Kurve ruht ganz im homogenen elektrischen Feld E' des BZS K'. c) Wählt man eine beliebige geschlossene Kurve aus guten Leitern, die die Flügel (den Stab) enthält, und die im Bezugssystem K' ruht, so kann ebenfalls keine Spannung gemessen werden, aus zwei Gründen: 1. Es konnte sich das sekundäre Feld E nicht ausbilden. 2. Wie oben. In keinem dieser drei Fälle gibt es eine Änderung des magnetischen Flusses in der geschlossenen Kurve und keine Induktion.

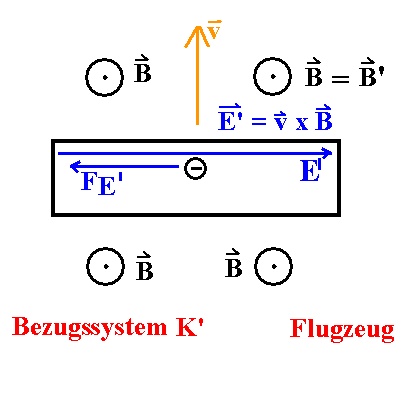Abb. 4: Man stelle sich vor, die Enden der Flügel gleiten auf gut leitenden Drähten im Erdsystem K. Dann kann das sekundäre Feld E nicht entstehen. Es gibt in einer so definierten geschlossenen Kurve aber eine Ringspannung und einen Ringstrom. Das Feld E' trägt nur innerhalb der Flügel bei.

d) Induktion mit einer Änderung des magnetischen Flusses erhält man erst in der üblichen Weise, wenn man den bewegten Stab durch eine Leiterschleife ergänzt, von der Teile anderen Bezugssystemen angehören. Man wählt also eine beliebige geschlossene Kurve, von der die Flügel (den Stab) einen leitfähigen Teil bilden und die  überwiegend im Bezugssystem K ruht (das Flugzeug gleitet auf z.B. leitfähigen Drähten). Dann kann ein sekundäres elektrisches Feld E nichts zum Umlaufsintegral über das elektrische Feld beitragen, weil sich Beiträge - wie bei jedem Potenzialfeld - gegenseitig aufheben. Wenn die geschlossene Kurve aus guten Leitern bestehen, gibt es das sekundäre elektrische Feld E gar nicht. Es gibt aber noch den Beitrag vom elektrischen Feld E'. Er kann nur im bewegten Teil, also in den Flügeln wirksam werden. Zum Umlaufsintegral für die Arbeit beim Transport der Ladung q bei einem vollen Umlauf in einer solchen Kurve gibt es einen einzigen Beitrag: - ∫ 0  F·ds  = - q ∫ 0  E'·ds  =  q· v· B·ℓ . (Wir achten wieder nicht auf Vorzeichen und interessieren uns nur für den Betrag.) Es ergibt sich eine Umlaufspannung mit dem Betrag U0 = v· B·ℓ  . Es handelt sich um eine Induktionsspannung, die einen Ringstrom gemäß U0 = R · I  antreibt, wenn R der Gesamtwiderstand des leitenden Rings ist. Es überrascht nicht, dass das Ergebnis für die Ringspannung U0 =  B·v·ℓ unabhängig vom Bezugssystem ist, in dem die Vorgänge in den Flügeln betrachtet werden. Das gilt auch, wenn die Regel angewendet wird: Betrachte für das integrale Induktionsgesetz (die "Flussregel") einen geschlossenen Weg in dem System oder den Systemen, in dem die Ringspannung gemessen wird. Dann wäre System K' anzuwenden, ergänzt durch lokale BZS der Schleife.

Der Flugpassagier stellt also fest: Ich kann mir überlegen, dass sich der linke Flügel negativ auflädt. Ich kann aber weder das noch eine Spannung zwischen den Flügelenden experimentell nachweisen, weil im Flugzeug keine Kräfte auf Ladungen nachweisbar sind. Im System des Flugzeugs gibt es eine solche Spannung nicht, weil  sich im isolierten Flugzeug die elektrischen Felder aufheben.

Man sieht auch, dass die in in der Elektrostik wichtigen Potenzialdifferenzen hier wie in anderen Fällen stationärer Ströme keine exakte physikalische Bedeutung haben. Es wird daran erinnert, dass die Ringspannung gemäß  - ∫ ₀  E'·ds = I·R mit einem Strom I verbunden ist, wenn der Gesamtwiderstand der Stromschleife R ist.

Für den Unterricht ergeben sich daraus folgende Konsequenzen:

1. Die übliche Herleitung der Induktionsspannung "bei einem bewegten Leiter" liefert zwar den richtigen Betrag der Induktionsspannung, kann aber den Induktionsstrom nicht erklären. Dieser ist ja ein Ringstrom. Dazu braucht man mindestens die Lorentzkraft, die durch den Trick mit der Erzeugung des sekundären elektrischen Felds gemessen wird, aber eben dann, wenn es diesen Ringstrom nicht gibt. (Von einer "Induktion in einem bewegten Leiter" zu sprechen ist mit Sicherheit nicht sinnvoll, da jeder Leiter bewegt ist oder ruht, je nach Bezugssystem, und weil die Induktion nicht speziell im Leiter stattfindet, sondern nichtlokal verteilt irgendwo im Bereich, wo sich der magnetische Fluss ändert.)

2. Klarer wäre es m.E., wenn Induktion auch in der Schule in jedem Fall mit einer Umlaufspannung (Ringspannung) verbunden wird. Diese wird wie die gewöhnliche Spannung  (falls eine Potenzialdifferenz vorliegt) gemäß DIN 1324 definiert als Arbeit pro Ladungsmenge. In den schulisch wichtigen Fällen lässt sie sich immer stückweise berechnen, weil in einem bestimmten Abschnitt entweder die Kraft konstant ist (Lorentz-Kraft in einer im Magnetfeld bewegten Leiterbrücke bzw. entsprechende elektrische Kraft gemäß der RT), oder weil sie verschwindet (auf den Leiterstücken außerhalb der im Magnetfeld bewegten Leiterbrücke), oder weil Symmetrieargumente nahelegen, dass der Betrag des bei der Induktion entstehenden elektrischen Feldes längs des ganzen Leiterrings konstant ist, wie z.B. bei der so genannten "Induktion in einem ruhenden Leiterring", wenn sich etwa in einer kreisförmigen Leiterschleife der magnetische Fluss zeitlich ändert. Auf Integrale kann man dann ganz verzichten. Solche Herleitungen machen in der Schule kaum mehr Schwierigkeiten, leiten aber eine (Ring-)Spannung her, die wirklich als Ursache des Induktionsstrom gesehen werden kann.

Von einer Ringspannung spricht man, wenn die Arbeit zum Transport einer Ladung auf einem geschlossenen Weg von Null verschieden ist. Bei einem Potenzialfeld wie in einem Kondensator gibt es keine Ringspannung. Sie wäre 0. Denn um eine positive Probeladung von der negativen zur positiven Platte im Inneren des homogenen Kondensatorfelds zu bewegen, muss man dem Betrag nach die gleiche Arbeit aufwenden, die wieder frei wird, wenn die positive Probeladung im Außenraum (oder auch im Innenraum) vom Pluspol zum Minuspol zurückfließt. Wegen der Wegunabhängigkeit des Potenzials ist das bei jedem Potenzialfeld so.

Um eine positive Probeladung vom negativen (1) zum positiven (2) Pol im Kondensatorfeld zu verschieben, muss eine äußere Kraft F_ext = - q·E aufgewendet werden. Deshalb wächst dabei durch die zugeführte Arbeit die potenzielle Energie der Probeladung, und es gilt U₁₂ = 1/q ∫ ₁²  F_ext·ds  = - 1/q ∫ ₁²  F·ds =  - ∫ ₁²   E'·ds > 0 (da E' und ds entgegengesetzt; F  = - F_ext ist die Kraft des Felds auf die Ladung q , wenn durch eine von außen aufgewendete Kraft F_ext nicht auch noch kinetische Energie zugeführt werden soll). U₁₂ ist die gewöhnliche Spannung oder Potenzialdifferenz am Punkt 2 im Vergleich zum Punkt 1 (wenn sie existiert).

Bei der Induktion entsteht dagegen eine von Null verschiedene Ringspannung innerhalb der geschlossenen Kurve, innerhalb der sich der magnetische Fluss ändert. Bei der Induktion entsteht z.B. ein ringförmiges elektrisches Feld, das Leitungselektronen im geschlossenen Stromkreis immer wieder im Kreis herumtreibt. An einer Ladung q wird  analog bei einem vollen Umlauf die Stromarbeit W = - ∫ ₀  F·ds verrichtet, die die Verluste, z.B. durch Wärmeabgabe, ausgleicht. Dabei ist F die Kraft des bei der Induktion entstehenden elektrischen Feldes (deshalb das Minuszeichen). Als Ringspannung  U₀  (die kleine ₀ soll ein Kreissymbol sein) wird dann analog zur Potenzialdifferenz definiert:

Wenn nicht nur elektrische Kräfte auf dem Umlauf wirken, scheint es naheliegend, auch solche Kräfte in F bei der Definition von U₀ zu berücksichtigen. Diese Definition der Ringspannung ist mit DIN 1324 kompatibel.

Bei einem Potenzialfeld gibt es Wegabschnitte, auf denen Arbeit verrichtet wird, die auf anderen Wegabschnitten wieder gewonnen wird. Deswegen ist hier die Ringspannung 0 und wird üblicherweise nicht betrachtet. Ein durch ruhende Ladungen erzeugtes elektrisches Feld ist immer ein Potenzialfeld.

(zurück)

Vergleichen Sie - alternativ zur obigen Argumentation - die beiden Herleitungen:

a) In Schulbüchern findet man folgendes Vorgehen: Es wird der isolierte Stab betrachtet und wie oben die elektrostatische Spannung als Folge des sekundären elektrischen Felds E, U = B· v· ℓ,  berechnet. Es wird dann einfach behauptet, man könne diese Spannung an den Enden des Stabs mit leitenden Verbindungen zum Spannungsmesser abgreifen, und diese Spannung sei auch Ursache des Induktionsstroms.

b) In einfacheren Hochschulbüchern findet man folgendes Vorgehen: Wenn der Leiterstab auf leitenden Schienen gleitet, fließt ein Strom. Dann verrichtet die Lorentz-Kraft an einem Leitungselektron mit der Ladung e (Betrag) die Arbeit W = F_L . ℓ, weil nur im Stab die Lorentz-Kraft als "Antrieb" der Leitungselektronen dienen kann. Nach der Definition der Spannung/Potenzialdifferenz  U =  W/Q = W/e erhält man also U = B· v· ℓ .

Meines Erachtens bleibt bei der Methode a) der Zusammenhang zwischen den zwei verschiedenen Situationen offen: (1) isolierter Stab / Ausbildung einer elektrostatischen Spannung durch das sekundäre elektrische Feld E und (2) fehlendes sekundäres elektrisches Feld E und Fehlen einer elektrostatischen Spannung bei Verbindung der Enden mit einem gut leitenden Leiterbügel. Die "Formel" kommt natürlich richtig heraus.

Methode b) entspricht weitgehend dem hier vorgeschlagenen Weg über die Ringspannung, weil der einzige Beitrag zur Ringspannung vom Wegstück innerhalb des Leiterstabs kommen kann. Lediglich der letzte Satz erscheint mir insofern problematisch, als der Leser möglicherweise glaubt, hier entstehe wirklich eine Potenzialdifferenz und eben keine Ringspannung/Umlaufspannung. Mit wenigen Worten ließe sich Methode b) zur hier vorgeschlagenen Methode modifizieren.

Eine ganz andere Frage ist, wie die Ringspannung gemessen wird.

Betrachten wir das System des Towers K. Die Flügel (der leitende) Stab gleiten auf leitfähigen Drähten, die zu einem statischen Spannungsmesser führen. (Moderne Spannungsmesser mit Eingangswiderständen von vielen MOhm können als solche angesehen werden.) Ohne Strom kann es nicht zu einem Spannungsabfall zwischen Flügel und Spannungsmesser kommen (bei beliebiger Leitfähigkeit der Drähte); es bildet sich das sekundäre Feld E mit seiner Potenzialdifferenz aus. Der Spannungsmesser misst also direkt die Potenzialdifferenz des sekundären elektrischen Felds, das im Flügel den Betrag E = v · B hat. Die zugehörige Potenzialdifferenz U = E·ℓ = v · B · ℓ ( ℓ ist die Spannweite der Flügel) gilt wegen der Wegunabhängigkeit des Potenzials für jeden beliebigen Weg, also auch für den Weg über die leitenden Drähte und den Spannungsmesser. Sie entspricht der Ringspannung.

Eine ganz andere Situation liegt vor, wenn eine feste kreisförmige Leiterschleife mit dem Umfang 2·r·p von einem zeitabhängigen Magnetfeld durchsetzt wird. Längs der Leiterschleife entsteht durch Induktion zunächst ein elektrisches Wirbelfeld. Bei einer geschlossenen Leiterschleife erzeugt es einen Ringstrom. Bei einer offenen Leiterschleife dagegen verschiebt es Ladungen bis an die Enden und es entsteht ein sekundäres elektrisches Potenzialfeld. Die Ladungsverschiebung ist beendet, wenn Kräftegleichgewicht im Inneren des Leiters entstanden ist. Dann haben dort die elektrische Wirbelfeldstärke und die des Potenzialfelds gleichen Betrag. Beträgt die Länge des offenen Leiterrings ℓ hat die Potenzialdifferenz den Betrag E· ℓ im Vergleich zur Ringspannung E·2·r·p. Bei geringem Abstand der Enden der Leiterschleife stimmen beide weitgehend überein. Mit einem statischen Spannungsmesser zwischen den Enden kann man also die Ringspannung in guter Näherung als Klemmenspannung messen. Bei einer Spule, bei der viele volle Windungen hintereinander geschaltet sind, macht sich der kleine Unterschied kaum bemerkbar.