|
Aufgabenbeispiel
|
Einige "einfache" Aufgaben zur Induktion
|
Diese Aufgaben sind dazu geeignet, dass sich der Lehrer selbst eine
Übersicht über die Thematik verschafft.
Es soll nicht angeregt werden, die Inhalte
davon in den Schulunterricht zu übernehmen.
Die Behandlung dieser Aufgaben im Unterricht könnte für Schüler
evtl. sogar kontraproduktiv sein. Damit der Lehrer aber nicht in Versuchung
gerät, falsche Vorstellungen weiterzugeben, empfiehlt es sich, sie
gründlich zu studieren.
Vgl. Brandt, S., Dahmen, H.D.: Physik, eine Einführung in Experiment
und Theorie, Bd. 2, Elektrodynamik, Springer-Verlag, 1986.
Eine Rückwirkung des Induktionsstroms auf den magnetischen Fluss soll
vernachlässigt werden. Im Hinblick auf die Lenz'sche Regel scheint das
zunächst problematisch. Es sind jedoch Parameter wählbar, so dass
der Induktionsstrom klein sein kann und deshalb nur einen kleinen Gegenfluss
erzeugt. Ein anderes richtiges Argument ist, dass in alle Feldgleichungen
eigentlich nicht die Felder "vor dem Effekt" eingehen, sondern die Felder
"während des Effekts", also die durch den Effekt evtl. bereits
veränderten Felder. Wie man diese so erzeugen kann, dass sie genau den
folgenden Aufgaben entsprechen, bleibt offen.
Aufgabe 1:
Eine rechteckige Leiterschleife mit den Abmessungen l und a bewege sich mit
konstanter Geschwindigkeit v auf einen rechteckig begrenzten Magnetfeld-Bereich
zu, in dem eine konstante magnetische Flussdichte B herrscht, und dann durch
den Magnetfeld-Bereich hindurch. Die Leiterschleife soll verschwindenden
elektrischen Widerstand haben.
a) Entscheiden Sie spontan (Spannung im Sinn von Potenzialdifferenz):
Klicken Sie Ihre Wahl an! |
|
|
b) Berechnen Sie die Änderungsrate des magnetischen Flusses!
c) Stellen Sie die Ringspannung in Abhängigkeit von der Zeit dar!
d) Berechnen Sie den Induktionsstrom in Abhängigkeit von der Zeit und
stellen Sie ihn - passend zur Zeichnung von Aufgabe c) graphisch dar!
Lösung:
Zu b)
Keine Induktion findet statt, wenn sich die Leiterschleife ganz außerhalb
des Magnetfelds befindet oder ganz im Magnetfeld. Nur wenn sich der magnetische
Fluss ändert, findet Induktion statt. Zur Zeit t = 0 beginne die
Leiterschleife, ins Magnetfeld einzutreten.
Beim Eintritt:
DF =
B·v·Dt·l
Daraus ergibt sich eine Ringspannung Ui = -
DF /Dt = -
B·v·l. Ebenso erhält man beim Austritt:
DF = -
B·v·Dt·l
bzw.
Ui = B·v·l
In beiden Fällen hängt die Ringspannung von der Geschwindigkeit
der Leiterschleife ab, wie man es auch erwartet.
Zu c)
Durch die Lorentz-Kraft auf die Elektronen im Leiterbügel, der sich
im Magnetfeld bewegt, werden alle Leitungselektronen im ganzen Leiterring
in Bewegung gesetzt. Es soll angenommen werden, dass es keine Stoßwellen
von Elektronendichten gibt, sondern dass sich die Elektronen überall
im Ring instantan in Bewegung setzen.
Die Elektronendichte (der Leitungselektronen) sei n. Die einheitlich angenommene
Querschnittsfläche des Leiters sei A. In einem Volumen der Länge
x befinden sich dann n·A·x Elektronen.
Beim Eintritt:
In der Zeit Dt wird auf die Elektronen im
Leiterbügel der Länge l ein Kraftstoß bzw. ein Impuls
übertragen. Betroffen sind n·A·l Leitungselektronen,
die alle die Lorentz-Kraft e·v·B erfahren. Daraus
ergibt sich insgesamt eine Impulsänderung um
Dp = n·A·l.
e·v·B· Dt.
Diese wird an alle Leitungselektronen übertragen, also an
n·A·2·(l+a). (Hier geht also die ganze
Länge, der Umfang, des Leiterrings ein.) Indem diese bei einer Gesamtmasse
m =
n·A·2·(l+a)·me
beschleunigt werden, stellt sich eine einheitliche Geschwindigkeit u ein,
die mit der Zeit Dt wächst. Es gilt:
u = Dp/m =
e·v·B·Dt·l/(
2(l+a)·me )
In der Zeit Dt strömen
n·A·u·Dt
Elektronen an einer Messstelle vorbei und es ergibt sich die Stromstärke
I =
n·A·u·Dt·e/Dt =
n·A·u·e =
n·A·e2·v·B·l/(
2(l+a)·me
)·Dt =
n·A·e2·v·B/(
2(1+a/l)·me
)·Dt . Mit dem jeweils die
Leiterschleife durchsetzenden magnetischen Fluss
DF =
v·l·B·Dt
erhält man:
| I = n·A·e2/(
2(l+a)·me )·DF
|
Das ist ein bemerkenswertes Ergebnis:
1. Es besagt, dass trotz des verschwindenden Widerstands die
Stromstärke endlich bleibt! Grund ist die Trägheit der
Leitungselektronen, die erst allmählich durch das elektrische Feld in
Bewegung gesetzt werden. Offenbar gilt das Ohmsche Gesetz nicht!
2. Die Stromstärke ist proportional zum jeweiligen die
Leiterschleife durchsetzenden magnetischen Fluss
DF. Sie hängt sonst nicht mehr von der
Geschwindigkeit ab.
3. Sie hängt vom Leitermaterial ab und zwar über
die Ladungsträgerdichte n.
Solange sich die Leiterschleife ganz im Magnetfeld bewegt,
bleibt dieser Strom auch ohne weitere Induktion(sspannung) bestehen, weil
die Elektronen keinen Widerstand erfahren. Wegen ihrer Trägheit bewegen
sie sich ungebremst weiter. Hier liegt also ganz klar ein elektrischer
Strom ohne Spannung als Ursache vor!
Beim Austritt erfahren sie wieder eine Lorentz-Kraft in umgekehrte
Richtung und werden abgebremst. Auch insgesamt ergibt sich die
Proportionalität zwischen der Stromstärke und dem magnetischen
Fluss DF, der die Leiterschleife senkrecht durchsetzt.
4. Die Verhältnisse hier sind ganz anders, wenn
die Leiterschleife einen endlichen Widerstand hat. Dies wird in der
Regel bei Aufgaben in der Schule oder z.B. bei einer Grundkurs-Abituraufgabe
stillschweigend vorausgesetzt. In jenem Fall sind Spannung U und
Stromstärke I zueinander proportional, haben also gleichen Zeitverlauf.
Dann verschwinden auch Induktionsstrom und Ringspannung, wenn sich die
Leiterschleife ganz im homogenen Feld bewegt! Bei einem
endlichen Widerstand wäre I prop. zu U und damit zur Zeitableitung
von F!
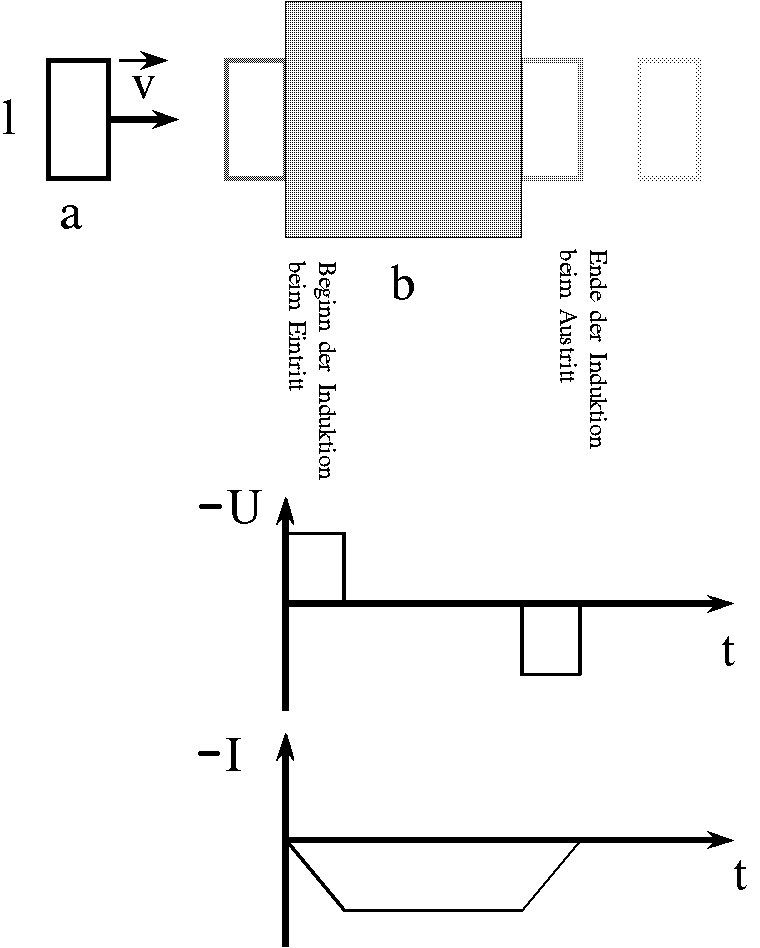 |
Zu Aufgabe 1: Bewegung einer widerstandslosen Leiterschleife
mit konstanter Geschwindigkeit durch einen Bereich mit homo-
genem Magnetfeld: Obwohl im Inneren des Magnetfeldbereichs
keine Induktion stattfindet, fließt dort ein konstanter Induktions-
strom, ganz anders als im schulisch üblichen Fall!
|
Aufgabe 2:
Eine kreisförmige Leiterschleife vom Radius r mit verschwindendem
elektrischen Widerstand soll senkrecht von einem zeitlich veränderlichen
Magnetfeld durchsetzt werden.
a) Berechnen Sie die Ringspannung, wenn für B gilt : B = B0
sin (w t)!
b) Berechnen Sie die Stromstärke I des Induktionsstroms dabei!
c) Stellen Sie die Zeitabhängigkeit von magnetischem Fluss
DF , Ringspannung U und Stromstärke
I in geeigneten Diagrammen einander gegenüber.
Lösung:
Zu a)
Bei konstanter Windungsfläche A =
r2p gilt für den magnetischen
Fluss F:
F = B·A =
r2pB
Für die Ringspannung erhält man durch Zeitableitung:
U = - DF/Dt = -
r2pB0·w·cos (
w·t)
Hieraus ergibt sich für das Wirbelfeld längs des Leiterrings eine
elektrische Feldstärke E = U/(2rp) = - 0,5
rB0·w·cos
(w·t)
Zu b)
Im Leiter befinden sich
n·A·2·r·p
Leitungselektronen. Auf jedes einzelne wirkt eine elektrische Kraft F
= e·E
F = - 0,5
e·r·B0·w·cos
(w·t)
Daraus ergibt sich die Beschleunigung jedes einzelnen Elektrons zu
a = - 0,5
e·r·B0·w/me
cos(w·t)
Durch Integration erhält man die Geschwindigkeit eines
Leitungselektrons ( u(t=0) = 0 )
u = -
0,5·e·r·B0/me
sin(w·t)
Für die Stromstärke ergibt sich damit wieder
I =
n·A·u·Dt·e/Dt = -
ne2·A·0,5·r·B0/me·sin(w·t)
oder mit F =
r2pB0·sin
(w·t):
| I = -
n·e2·A/(2·r·p·me) · F |
Die Stromstärke I in einer widerstandslosen
Leiterschleife ist damit wieder proportional zum momentanen magnetischen
Fluss F! Bei einem endlichen Widerstand
wäre I prop. zu U und damit zur Zeitableitung von
F!
Folgerungen für die widerstandslose Leiterschleife:
1. Stromstärke und Ringspannung sind
phasenverschoben.
2. Der Induktionsstrom hängt (außer indirekt über
F ) im Unterschied zur Spannung nicht von der
Frequenz ab, mit der sich das Magnetfeld ändert.
3. Der Induktionsstrom hängt vom Leitermaterial ab, und
zwar über die Dichte der Leitungselektronen n.
Aufgabe 3:
Versuchen Sie, auch für den allgemeinen Fall der Induktion längs
eines widerstandslosen geschlossenen Leiters der Länge l die
Vermutung zu beweisen:
Es ist dann noch zu überlegen, ob diese Verhältnisse
näherungsweise auch noch gelten, wenn der Widerstand sehr klein ist
(im Vergleich zu welchem anderen? Vgl. Drude-Lorentz-Modell
der Leitfähigkeit, z.B. in Gerthsen/Vogel/Meschede.).
Hinweise:
1. Hat der Leiter einen nicht verschwindenden ohmschen Widerstand,
sind die Aussagen hier sehr stark zu modifizieren. Aus dem Ohmschen Gesetz
j = s
· E sollte sich hier eine
Proportionalität zwischen I und U ergeben! Vgl.
Drude-Lorentz-Modell der Leitfähigkeit, z.B.
in Gerthsen/Vogel/Meschede.
2. Durch die vorstehenden Überlegungen ist wieder einmal
geklärt: Nicht in jedem Fall ist eine Spannung U als Ursache eines Stromes
nötig. (Newton wirkt auch hier!)
3. Es wird klargestellt, dass das elektrische Wirbelfeld Ursache
für den elektrischen Strom ist, hier, beim widerstandslosen Leiter,
also für das Verändern des elektrischen Stromes.
Aufgabe 4:
Wechselstrom durch Leiter ohne Widerstand
An einem widerstandslosen Leiter der Länge l mit der
Querschnittsfläche A soll eine Spannung U =
U0·sin(w·t) angelegt
werden. Daraus ergibt sich eine elektrische Feldstärke E = U/l und auf
jedes Leitungselektron die Kraft F = e·U/l. Dies führt zu
einer Beschleunigung aller Leitungselektronen des Drahtstücks a =
eU0/(l·me)·sin(w·t) . Nach Integration
erhält man wieder für die Elektronengeschwindigkeit u =
e·U0/(l·me·w)·cos(w·t)
.
Daraus ergibt sich die Stromstärke
I =
n·e·A·u·Dt/Dt =
n·e2·A·U0/(l·me·w)·cos(w·t)
.
Wieder stellt man fest:
1. Bei fehlendem Ohmschen Widerstand sind U und I gegeneinander
um 900 phasenverschoben: Der Leiter nimmt (gemittelt über
eine Periode) keine Energie auf.
2. Eine endliche Spannung U führt nicht zur beliebig großen
Stromstärke, die man bei verschwindendem Widerstand erwarten würde.
Es ergibt sich ein Wechselstrom mit der Amplitude I0 =
n·e2·A·U0/(l·me·w). Daraus ergibt sich für den Leiter der Länge
l ohne ohmschen Widerstand ein Wechselstromwiderstand R =
l·me·w /
(n·e2·A).
Hinweise:
1. Diese Überlegungen sind mit einer der
London-Gleichungen der Supraleitungstheorie eleganter
durchzuführen. Dort wird nämlich allgemein eine Beziehung zwischen
Stromdichte und elektrischer Feldstärke hergeleitet:
Jedes Leitungs-Elektron wird durch die elektrische Kraft mit
dem Betrag e·E beschleunigt. Es gilt
also:
(1)
me·a =
e·E
andererseits gilt für die Stromdichte j (Stromstärke
pro Querschnittsfläche A):
j =
n·u·e bzw.
dj/dt = j· =
n·a·e,
also nach Multiplikation der Gleichung (1) mit
n·e/me:
n·e·a =
n·e2/me·E.
Damit lautet die erste London-Gleichung für die zeitliche
Ableitung der Stromdichte:
Das Programm für die vorstehenden Aufgaben ist also stets
folgendes: Aus der Induktion folgt die elektrische Feldstärke E
des Wirbelfeldes (auch bei Benutzung der Lorentz-Kraft gilt ja im mit dem
Leiter mitbewegten Bezugssystem: E = v x B). Dann wird
die London-Gleichung (2) integriert und liefert die Stromdichte j bzw. die
Stromstärke I. Wegen dieser Integration veränderte sich in Aufgabe
1 die Stromstärke linear, kam in den Aufgaben 2 , 3 und 4 die
Phasenverschiebung zwischen Ringspannung bzw. Spannung und Stromstärke
zustande.
2. Beim widerstandslosen Leiter mit einer angelegten
Wechselspannung besteht eine nicht verschwindende elektrische Feldstärke
zwischen den Enden des Leiters, obwohl man das nach dem - hier nicht
gültigen - Ohmschen Gesetz mit j =
s·E
mit s ->
¥ nicht erwarten
würde.
Eine andere Form der London-Gleichung ist j(r) =
-e2·n/me·A(r).
Berechnet man das Kurvenintegral über einen geschlossenen Stromweg
(òo), erhält man
òo j(r)
· dr =
-e2n/me
òo
A(r)·dr
=
-e2n/me
ò rot
A(r)·df (wegen des Stokesschen
Satzes)
=
-e2n/me ·
F (wegen rot A = B,
die magnetische Flussdichte)
Bei konstanter Stromdichte j längs des geschlossenen Leiters der Länge
l und der Querschnittsfläche A erhält man also für die
Stromstärke I:
| (3) I = -
e2n/me · A/l ·
F |
Die Gleichung stimmt bis auf das Vorzeichen mit dem früher elementar
hergeleiteten Ergebnis überein und verknüpft also direkt I und
den magnetischen Fluss F.
(zuletzt aktualisiert Juni 2013)
