|
Stichwort
|
Mangel und Überschuss von
Ladungen an den Polen einer Batterie
Zur aktuellen Diskussion über
Oberflächenladungen bei stromdurchflossenen Leitern
|
.
Vgl. auch Der stationäre Strom im geschlossenen
Stromkreis und das Büchlein des Autors "Der
einfache elektrische Stromkreis - altes Wissen und neue Erkenntnis".
1. Unbestritten ist, dass ein solcher
Ladungsüberschuss bzw. Ladungsmangel an den Polklemmen einer unverbundenen
Gleichspannungsquelle (Batterie) herrscht. Seine Größe ist bestimmt durch
die Spannung der Batterie und die Kapazität zwischen den Polklemmen.
Ebenfalls unbestritten ist, dass sich durch zusätzliche metallische
Anschlüsse die Kapazität ändert, so dass der
Ladungsüberschuss bzw. Mangel verstärkt wird. Hat diese Kapazität
irgendeinen Einfluss auf den Stromfluss im geschlossenen Stromkreis, einen
Einfluss, der rechtfertigen könnte, ihn im Schulunterricht zu
thematisieren?
|
Das Kondensator-Modell
(1) Im geschlossenen Stromkreis liegt nämlich eine völlig
andere Situation vor. Der Kondensator zwischen den Polklemmen
(Kapazität C) und die Leitungskapazitäten C' spielen keine Rolle
mehr für den Strom I. Wenn der Stromkreis geschlossen wird, kommt
es zu schwer überschaubaren Ladungsverschiebungen mit der
Ausbildung bestimmter elektrischer Felder in den Leitern
(Einschaltvorgang). Sie passen schließlich zum stationären Strom,
der sich nach kurzer Zeit einstellt. Erst dieser interessiert in
der Schule.
Es ist dann egal, ob wir uns vorstellen, dass auf die gedachten
Kondensatoren in der Zeiteinheit gleich viele Ladungen zu- wie
abfließen, oder dass gar keine Ladungen zu- und abfließen.
Positive und negative Ladungen auf entgegengesetzten
Kondensatorplatten "halten sich gegenseitig fest auf ihren
Positionen". Von da ab haben sie keine Funktion mehr für den
Stromfluss; sie nehmen insbesondere nicht am Stromfluss teil. Der
Strom fließt jetzt im Inneren der Leiter "direkt" aus der
Stromquelle durch die Polklemmen in den Stromkreis.
Aufgabe der Stromquelle ist es jetzt nur noch, im
Stromkreis vorhandene Ladungen in Bewegung zu setzen und in
Bewegung zu halten. Auch durch die Batterie fließt ein Strom
gleicher Größe wie durch den Rest des Stromkreises, in der Regel
transportiert durch andere Ladungen. Beim stationären Strom muss
in jedes beliebige Volumenelement des Stromkreises gleich viel
Ladung zu- wie abfließen. Das Gleichgewicht zwischen
zufließenden und abfließenden Ladungen wird an jeder Stelle des
Stromkreises durch die Kontinuitätsgleichung
geregelt. Es wird also um Folgerungen aus ihr gehen.
|
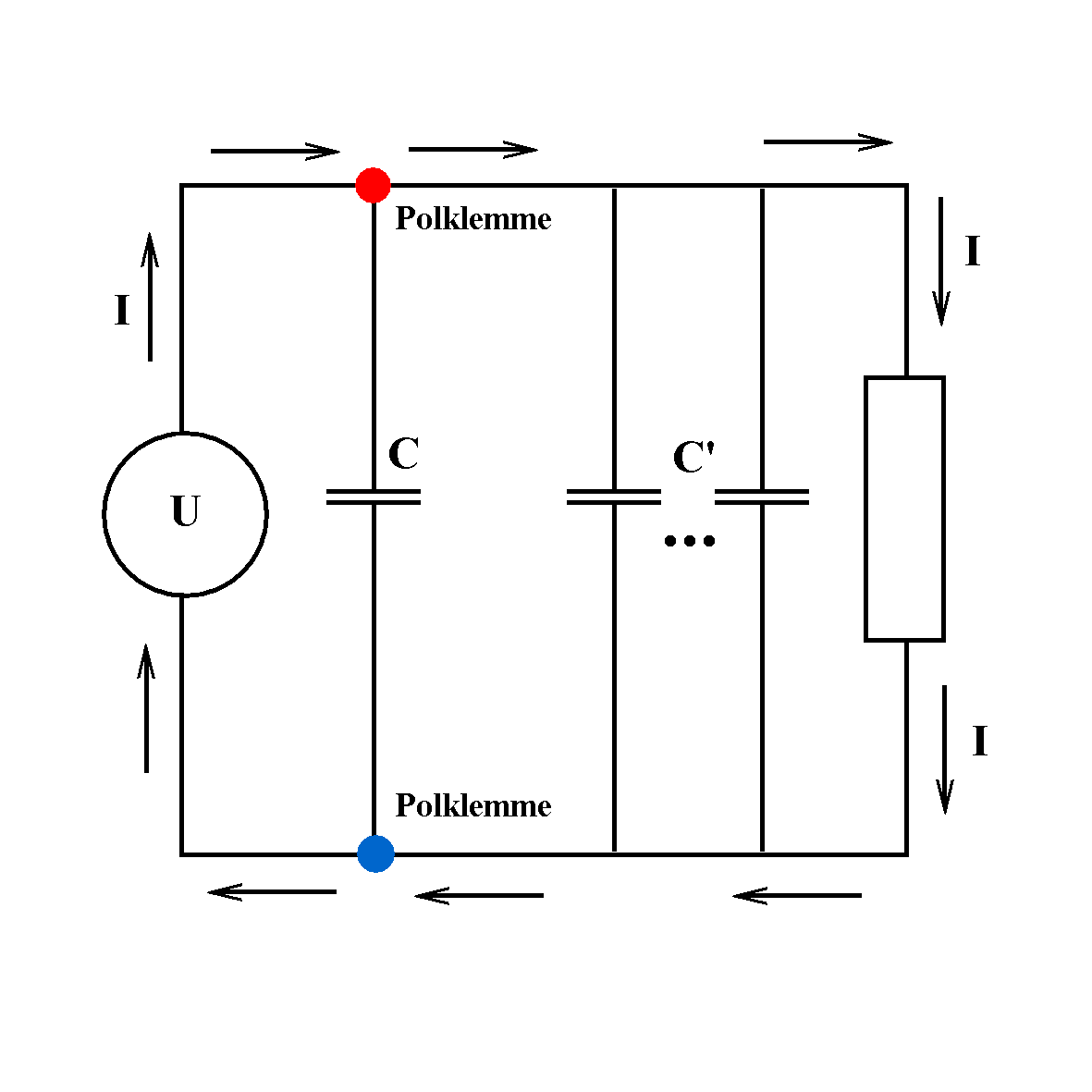
Abb. 1: Ersatzschaltbild
für Batterie mit dem gedachten Polklemmen-Kondensator, weiteren
Leitungskapazitäten und einem Widerstand. Wäre der Strom anders,
wenn diese Kapazitäten nicht vorhanden wären?
Sobald der stationäre Strom nach dem Einschaltvorgang erreicht
ist, nehmen die Ladungen dieser Kondensatoren nicht mehr am
Stromfluss teil.
Ihr elektrisches Feld, zusammen mit dem Magnetfeld, mit dem sich
der Strom umgibt, vermittelt aber den Energietransport. |
(2) Kontinuitätsgleichung und Ohm'sches
Gesetz bilden eine Art Zwangsbedingung für die
Entstehung von Bereichen mit Ladungsüberschuss und -Mangel in
den Leitern (Raumladungen) längs des Stromkreises durch einen
Strom. Aber auch die Mantelladungen auf der Oberfläche der Leiter
können durch beide bedingt sein.
Raumladungen und Mantelladungen schaffen den Rahmen (vor allem
modifizieren sie die jeweiligen elektrischen Felder) für den
stationären Strom durch die Leiter. Sie nehmen aber selbst
nicht am Stromtransport teil.
|
|
(3) Anderswo wird aber diskutiert, dass die von solchen
Oberflächenladungen ausgehenden elektrischen Felder und das
Magnetfeld als Folge des Stroms die wichtige Funktion haben, den
Energietransport
zu stromdurchflossenen Widerständen zu vermitteln. Die Energie
fließt dabei außerhalb der Leiter, aber vor allem in der
Umgebung der Leiter. Die Oberflächenladungen können keine
Energie liefern; diese stammt aus der Energiequelle /
Stromquelle.
|
(4) Soviel zu der manchmal zu hörenden Ansicht, ein Strom sei
der Versuch, Ladungsüberschuss an einem Pol und Ladungsmangel am
anderen auszugleichen, auch zu der Ansicht, ein Strom sei ein
Transport von gegenüber dem neutralen Leiter zusätzlichen
Ladungen, eben Überschussladungen. Abb. 1 sagt uns, dass die
mit den gedachten Kondensatoren zusammenhängenden Überschussladungen
nicht am stationären Stromtransport teilnehmen, weil sie
durch gleich viele entgegengesetzte auf der zweiten
Kondensatorplatte "festgehalten" werden.
Ähnliches gilt auch für andere statische Ladungen, wie
Raumladungen und Mantelladungen (Oberflächenladungen). Zudem
geht von ihnen ein Potenzialfeld aus, das die notwendige
Energiezufuhr zur Erzeugung von
Stromwärme nicht erklären kann. |
Es gibt ein Beispiel mit offensichtlich anderen
Verhältnissen: Bei einer geschlossenen Induktionsschleife, die
von einem sich ändernden Magnetfeld durchsetzt wird, gibt es Pole (und
vermeintlich den Strom bewirkenden Überschussladungen) gar nicht.
Dennoch fließt ein Strom und gibt es eine Spannung, weil die im
Stromkreis vorhandenen und den Strom transportierenden Ladungen
durch ein elektrisches Wirbelfeld angetrieben werden. Allgemein sollte
es als Aufgabe einer Stromquelle gesehen werden, im Stromkreis bereits
vorhandene Ladungsträger in Bewegung zu setzen, "anzutreiben" (evtl.
gegen dissipative Kräfte). Der Versuch, einen Stromfluss durch
gegenseitige Abstoßung von Ladungsanhäufungen und Anziehung von anderen
zu erklären, kann höchstens in Spezialfällen gelingen.
Die Vorstellung von einem Ladungsüberschuss bzw. -mangel könnte für
Schüler den Vorteil haben, dass sie die Bewegungsrichtung der jeweiligen
Ladungsträger erkennen. Die Stromrichtung selbst ist eine reine Definitionsfrage.
Die Vorstellung wird sicher falsch, wenn sich die Schüler dazu denken,
dass sich die Ladungsträger von einem Bereich mit Ladungsüberschuss
durch coulombartige Kräfte gegenseitig abstoßen ("Elektronendruck" oder
"elektrischer Druck") und von einem Bereich mit Ladungsmangel durch
ebensolche Kräfte - vielleicht sogar zusätzlich (!) - angesaugt werden.
Vielmehr erfolgt der "Antrieb" in allen Fällen "von außen", also durch
das sich ändernde magnetische Feld (bei der Induktion) oder - im Fall
der Batterie - durch chemische "Kräfte" in ihrem Inneren, die bei
Stromfluss im Stromkreis vorhandene Ladungen in Bewegung setzen.
Dieses Phänomen ist begleitet von geeigneten elektrischen
Feldern längs des Stromkreises und magnetischen Feldern um die
stromdurchflossenen Leiter. Diese vermitteln den Energietransport.
.
2. Nun zur Untersuchung von "Ladungsanhäufungen" in
den Leitern des Stromkreises:
Wir betrachten dünne und scharf begrenzte Leiter,
in deren Innerem das elektrische Feld stets parallel zur
Leitermantelfläche orientiert und über einen Querschnitt hinweg von
konstantem Betrag ist. Das elektrische Feld folgt also der
Leitergeometrie. Ein Leiter bestehe aus zwei hintereinander geschalteten
Zonen mit den unterschiedlichen Leitfähigkeiten σ1 und σ2,
aber gleicher Querschnittsfläche A, die an ihren Stirnseiten
(Querschnitt) zusammenstoßen. Innerhalb jedes der beiden Abschnitte für
sich ist wegen rot E = 0 die Feldstärke E überall
gleich, unabhängig von den Leitfähigkeiten. Die Feldstärke in den beiden
Abschnitten seien E1 und E2. Weil die Stromstärke
I in beiden Abschnitten die gleiche ist, gilt mit dem Betrag der
Stromdichte j wegen I = j·A = σ·E·A:
σ1·E1·A = σ2·E2·A
σ1· E1 = σ2· E2
Wenn sich die Leitfähigkeit in einem Leiter überall gleicher
Querschnittsfläche A ändert, ändert sich die elektrische Feldstärke und
es gilt
d.h. die Feldstärken in den beiden Zonen
verhalten sich umgekehrt wie die Leitfähigkeiten. Würden sich auch die
Querschnittsflächen ändern erhielten wir E1/E2
= (σ2·A2)/(σ1·A1)
.
.
3. Die Anpassung des Betrags der Feldstärken erfolgt
durch Raumladungen in den Übergangszonen.
Dabei ist es klar, dass diese Raumladungen nicht Ursache für die
jeweiligen elektrischen Felder und schon gar nicht Ursache des Stroms
sind. Man sieht das daran, dass die Richtung des elektrischen Feldes mit
der Stromrichtung immer übereinstimmt, die also im
Falle einer Batterie außerhalb von ihr tendenziell vom Pluspol zum
Minuspol zeigt (in ihrem Inneren also tendenziell von Minus nach Plus).
Verfolgt man die Stromrichtung, stößt man in manchen Fällen erst
auf eine positive und dann auf eine negative Raumladung. Das ist dann
der Fall, wenn zwischen beiden Stellen die elektrische Feldstärke erhöht
werden soll, z.B. wegen erniedrigter Leitfähigkeit zwischen beiden
Stellen. Man könnte jedoch auch erst auf eine negative und dann auf eine
positive Raumladung stoßen, wenn zwischen beiden Stellen die Feldstärke
erniedrigt werden soll, z.B. wegen erhöhter Leitfähigkeit zwischen
beiden Stellen. In letzterem Fall wird die Feldrichtung
nicht etwa umgekehrt, sondern ebenfalls an die durch Spannung,
Widerstand und Stromdichte festgelegte Größe angepasst. Man könnte
allenfalls sagen, dass durch die Raumladungen Zusatzfelder "erzeugt"
werden, die die von der Spannungsquelle ausgehenden Felder überlagern
und größenmäßig anpassen, also erhöhen oder erniedrigen.
| Raumladungen im Stromkreis sind nicht
die Ursache für die elektrischen Felder, die den Strom
begleiten, sondern passen nur deren Größe (und evtl. Richtung)
an. |
Im Folgenden soll ein Fall studiert werden, wo auch in einem
geschlossenen Stromkreis Stellen mit Ladungsüberschuss und -mangel
entstehen, nämlich dort, wo sich die Leitfähigkeit σ des Leitermaterials
ändert. In zwei Modellrechnungen soll die Auswirkung auf die
Ladungdichte untersucht werden, wenn in einem bestimmten Leiterabschnitt
der Länge 2·a die Leitfähigkeit allmählich auf 0 herunter gedreht wird.
Der Querschnitt des Leiters A soll überall konstant sein. Die
Leitfähigkeit σ ist der Kehrwert des spezifischen Widerstands ρ. Es gilt
also σ = 1/ρ . Der spezifische Widerstand wird in diesem Text nicht
verwendet. Dagegen ist hier von der Ladungsdichte ρ die Rede
mit der Einheit A·s/m3 .
.
4. Ausgangspunkt der Überlegungen ist die
Kontinuitätsgleichung für einen Strom
Sie regelt das Gleichgewicht zwischen zu- und abfließenden Ladungen
über die Stromdichte j. Mit dem Ohm'schen Gesetz für die
Stromdichte j = σ·E folgt, da diese im unverzweigten
Stromkreis unveränderlich ist:
div j = div (σ·E) = E·grad σ + σ · div E
= 0
Wir erhalten also div E = - ( grad σ · E ) /σ.
Das ist aber nach dem Gauß'schen Gesetz bis auf den Faktor 1/ε0
(mit der elektrischen Feldkonstanten ε0) gerade die gesuchte
Ladungsdichte:
| ρ = - (grad σ
· E) · ε0/σ
. |
Im homogenen Feld des Leiterinneren
in x-Richtung (bei entsprechender Leitergeometrie)
mit E = E ex gilt dann
ρ = - (∂σ/∂x
· E)· ε0/σ.
Eine von 0 verschiedene Ladungsdichte gibt es im Leiter also nur
an solchen Stellen, wo sich die Leitfähigkeit in x-Richtung ändert, falls
E ≠ 0. Den Faktor s = - ∂σ/∂x
· 1/σ nenne ich zum Gebrauch in diesem
Text "Leitfähigkeitsprofil".
| Im stromdurchflossenen
Stromkreis gibt es (im Inneren der Leiter) nirgends "gestaute"
Ladungen oder Ladungsanhäufungen außer an den Stellen, an denen
sich die Leitfähigkeit ändert oder - wie wir später sehen werden
- die Querschnittsfläche.
|
Ein geschlossener Stromkreis bestehe aus einer Batterie und einem
Lämpchen. Würde die Verbindungsleitung von Lämpchen und Pluspol einen
Überschuss an positiven Ladungen aufweisen (auf den gedachten
Kondensatoren, z.B. durch Oberflächenladungen) und die Verbindungsleitung
von Lämpchen und Minuspol einen Mangel an positiven Ladungen -
Entsprechendes gilt für negative Ladungen -, nähmen diese Ladungen nicht
am Stromfluss teil.
Beim Übergang zwischen Zonen unterschiedlicher Leitfähigkeit ändert sich
bei unveränderter Stromdichte j = σ · E die elektrische
Feldstärke E im Inneren des Leiters (nur im Gleichgewichtszustand
der Elektrostatik ist das Innere von Leitern feldfrei!). Beim Übergang von
hoher zu niedriger Leitfähigkeit muss die Feldstärke wachsen. Die
Anpassung der Feldstärken geschieht durch Raumladungen. Man erwartet, dass
bei großem Unterschied der Feldstärken auch eine dem Betrag nach große
Ladungsmenge erzeugt werden muss. Das Vorzeichen von ∂σ/∂x
entscheidet über das Vorzeichen der Raumladung.
Details der Ladungsdichte-Verteilung hängen stark von der Art des
Übergangs zwischen Bereichen unterschiedlicher Leitfähigkeit ab. In der
Regel kann man von einer Übergangszone von wenigen Atomlagen ausgehen. In
vergleichbarer Breite in x-Richtung entsteht dort eine Ladungsdichte-Zone
mit positiven bzw. negativen Raumladungen. Lässt man die Breite der
Übergangszone gegen 0 gehen, entsteht eine Flächenladungsdichte in einer
Ebene senkrecht zum Leiterquerschnitt ("Stirnladung"). Wegen der Division
durch σ, was auf der einen Flanke von ρ klein, aber der anderen groß ist,
kann man keine symmetrische Form der Ladungsdichteverteilug ρ bzgl. der
Mitte der Leitfähigkeitsflanke (in der Zeichnung bei +/-4 willkürlichen
Einheiten) erwarten.
Aber, wenn man in eine Übergangszone von atomarer Breite übergeht, wird
die Annahme von einer sich stetig verändernden Leitfähigkeit
problematisch.
Wir betrachten jetzt einen Widerstand mit einem Übergang
von einem Bereich großer Leitfähigkeit σ∞
zu einem Bereich geringer Leitfähigkeit
σ0.
Es gelte σ0
= σ∞/k
. (k = σ∞/σ0).
5. Rolle der Mantelladungen
Das Ohm'sche Gesetz wirkt zusammen mit der Kontinuitätsgleichung wie
eine Zwangsbedingung für die elektrische Feldstärke E bei einer
vorgegebenen Stromdichte j. Sie hatte schon festgelegt, dass im
Leiter höchstens an den Übergangsstellen verschiedener Leitfähigkeit
Raumladungen entstehen können, und dass j und E immer
gleichgerichtet parallel sind. Sie bestimmen in manchen Fällen auch die
Mantelladungen auf dem Mantel des Leiters. Evtl. zusammen mit äußeren
Ladungen (z.B. auf den Batteriepolen) ergibt sich daraus das elektrische
Feld im Außenraum des Leiters. Eine bestimmte Stromdichte j im
Leiter bestimmt also das elektrische Feld im Leiter und Raumladungen im
Leiter, aber auch Mantelladungen, die mit der konstanten elektrischen
Feldstärke im Leiter kompatibel sind. Das ergibt sich aus der Gleichung
ρ = - (grad σ · E) · ε0/σ
. Bisher kam es uns auf die Feldstärkekomponente im Leiter an.
Deshalb haben wir nur einen Leitfähigkeitsgradienten in x-Richtung
betrachtet. Außerhalb des Leiters, auf dem Mantel, gibt es aber auch
eine radiale Komponente der Feldstärke (senkrecht zum Leiter). Sie
liefert einen Zusatzbeitrag zur Ladungsdichte, ρM,
auf dem Mantel, also ρM = - (∂σ/∂r
· Er)· ε0/σ(r).
Eine relativ allgemeine Aussage können wir ohne
detaillierte Rechnung machen. Wenn sich aus ρM
eine Flächenladungsdichte/Verschiebungsdichte D auf dem
Mantel ergibt, folgt mittels des Gauß'schen Satzes D = ε0
· Er und damit
Er = D/ε0 .
Die Flächenladungsdichte nennen wir im Folgenden ρMF
. Ganz ähnlich hätte man für die elektrische Feldstärke im Leiterinneren
argumentieren können, wenn man die Breite der Raumladungszone gegen 0
streben lässt.
Wir stellen uns vor, dass σ(r) = σ(x)
im Leiterinneren wie oben, unabhängig von r, ist, dass σ(r)
innerhalb einer Übergangszone der Breite Δ
linear auf 0 abfällt und dann 0 bleibt. In bestimmten
Fällen verhält sich ρM genauso
wie σ(x), was sehr plausibel ist. ρM
ist dann nahe der Raumladungszonen konzentriert.
Also σ(r) = σ(x)·
(1-u) für R < r < R + Δ wobei u = (r - R)/Δ.
In der Mitte des Übergangsbereichs wird σ(r = R +
Δ/2) = <σ(r)>
= σ(x)/2. Dann ist in der Übergangszone
∂σ/∂r
= - σ(x)/Δ und wir
erhalten für ∂σ/∂r
/ <σ(r)> : - 2/Δ,
also ρM = 2/Δ·
Er· ε0. Eine Flächenladungsdichte ρMF
= ρM ·Δ/2 macht
auch noch einen Sinn, wenn die Breite der radialen Übergangszone Δ => 0
geht. Wir erhalten wie oben
ρMF = Er·ε0
. Die Flächenladungsdichte
ρMF
auf dem Mantel des Leiters ist ein Abbild der
Radialkomponente Er der elektrischen
Feldstärke außerhalb des Leiters. Wie gesagt: ρMF
ist bestimmt durch Kontinuitätsgleichung und Ohm'sches Gesetz, und zwar
so, dass E im Leiterinneren der Leitergeometrie folgt, und Er
ist durch ρMF
und andere Ladungen in der Umgebung des Stromkreises bestimmt.
(Mit Hilfe einer Theta-Funktion Θ(r) für die Leitfähigkeit
σ(r) und der δ(r)-Funktion als deren Ableitung hätte
man das gleiche Ergebnis schneller erhalten.)
ρFM hängt über die Kontinuitätsgleichung und
das Ohm'sche Gesetz vom Leiterinneren ab. Er
wiederum von ρFM,
andererseits von sonstigen Quellen des elektrischen Felds.
Deshalb gibt es wenig allgemeine Aussagen. Zwei Extrema: R.
Müller untersucht (qualitativ)
die Rolle von Batterieladungen beim homogenen Leiterkreis mit
einheitlichem Widerstand pro Längeneinheit. Andererseits wird in
diesem Text nur ein stromdurchflossener Widerstand ohne weitere äußere
Ladungen beschrieben. Letzteres würde eher zur inhomogenen
Induktionsschleife (mit unterschiedlichen Widerständen) ohne weitere
Energiequelle passen.
Während des kurzzeitigen Einschaltvorgangs verschiebt die
sich ausbildende Stromdichte j Ladungen so in den
Raumladungsbereich und an den Mantel, dass Kontinuitätsgleichung
und Ohm'sches Gesetz erfüllt werden. Durch Raumladungen und
Mantelladungen ist dann im Leiter ein elektrisches Feld E
gesichert, das der Leitergeometrie folgt und unter idealen Bedingungen
im Leiterinneren konstant ist.
R. Müller berichtet von einem Zusammenhang
zwischen ρMF(x) und dem Winkel α zwischen Ex
und Er am Mantel, der sehr nützlich ist für qualitative
Überlegungen. Da tan(α) = Er/Ex erhält man also ρMF(x)=
ε0 Ex·tan(α). Müller weist darauf hin,
dass man in Zeichnungen des Stromkreises mit qualitativ eingetragenen E-Feldlinien
bzw. Äquipotenziallinien mit dem abgelesenen Knickwinkel α eine
Vorstellung von den sich ausbildenden Mantelladungen gewinnen kann,
auch, wenn das Feld außerhalb des Leiters durch externe Ladungen (z.B.
in der Energiequelle) mitbestimmt ist. Ohne externe Ladungen (z.B. in
einer Induktionsschleife) folgt dagegen analog, dass von einem Ende
eines Widerstands Feldlinien ausgehen, die am anderen Ende des
Widerstands wieder einmünden.
Nach Beendigung des Einschaltvorgangs brauchen wir uns
nicht weiter darum kümmern, wie j = σ · E für einen
stationären Strom erreicht wird. Im Folgenden betrachten wir
wieder ausschließlich das Leiterinnere.
6. Es sind zwei Fragestellungen denkbar:
a) Bei einer bestimmten Stromdichte mit
dem Betrag j = I/A = σ·E wird die Ortsabhängigkeit der
elektrischen Feldstärke bzw. von σ in Rechnung
gesetzt. Da j überall konstant, folgt E = j/σ = I/(A·σ). Die
Ladungsdichte ρ wird dann
ρ = - (∂σ/∂x)·1/σ
· E· ε0 = - (∂σ/∂x)·1/σ
·I/(A·σ) · ε0
= - (∂σ/∂x)·1/σ2·I/A
· ε0
(ρ
und σ sind ortsabhängig)
Für die Gesamtladung in einem solchen Raumladungsbereich
erhalten wir durch Integration, wenn a und b zwei geeignete
Koordinaten im guten bzw. im schlechten Leiter sind
Q = - ∫ (∂σ/∂x)·1/σ2
dx · I/A ·
ε0
· A mit den gleichen
Grenzen, oder
σ0
Q = -
∫ 1/σ2
dσ ·
I ·
ε0
σ∞
|
Q = ( σ∞
- σ0
)/ (σ∞
· σ0
) ·
I · ε0
oder mit dem "Leitfähigkeitssprung" k = σ∞/σ0
Q = (k - 1) ·
I/σ∞
· ε0 .
Bei Verwendung von Kupferleitungen zum Widerstand mit dem
spezifischen Widerstand 1/σ∞
= 1,56·10-8 V·m/A
und k = 42 (Größenordnung bei Cr-Ni-Widerstandsdraht) und I = 10A
erhalten wir
Q = 41 ·10 A·1,56·10-8
V·m/A ·
8,85·10-12 As/Vm ≈
566·10-19 As ≈
350·e
Diese Ladungsmenge ist überraschend gering: die
gesamte negative Raumladungswolke enthält in der Übergangszone zum
Widerstand nur ca. 350 Elektronen. Sie wächst, unabhängig vom
Leiterquerschnitt A, bei größerer Stromstärke I und größerem
Leitfähigkeitssprung k. Bei anderen Parameteränderung kann sie
auch kleiner gemacht werden. Hier - im Bereich atomarer Maßstäbe -
versagt wohl das Modell der stetigen Leitfähigkeitsänderung in der
Übergangszone.
b) Bei fester Batteriespannung U
soll der Widerstand vergrößert werden. Der Widerstand soll ein
langer Draht der Länge 𝓁 und
der Querschnittsfläche A sein. Nur für die Stromberechnung bei
der gegebenen Spannung U soll der Widerstand im Stromkreis allein
durch σ0 im Inneren des schlechten Leiters bestimmt
sein, d.h. die Spannung U soll ganz am Widerstand abfallen. Der
Widerstand der Stromzuführungen soll also vernachlässigbar sein; also
auch ein Spannungsabfall in den Stromzuführungen, was eine umso
bessere Näherung ist, je geringer die Leitfähigkeit σ0 im
Inneren des schlechten Leiters.
Es gilt dann I = U/R = U·A·σ0 /𝓁 mit den
Widerstandsdimensionen A und 𝓁, also R = 𝓁/(A·σ0).
Die Stromstärke ist überall im unverzweigten Stromkreis konstant;
entsprechend auch der Betrag der Stromdichte j = I/A = U·σ0 /𝓁
bei konstanter Querschnittsfläche A. Unter diesen Voraussetzungen gilt
nur für den Bereich des Widerstands E = U/𝓁 und
j = σ0·E = σ∞·E∞
, letzteres für den Teil des Stromkreises außerhalb des Widerstands.
Tatsächlich ist E∞ =
(σ0 /σ∞)
·E. Wenn im Widerstand die Leitfähigkeit σ0
kleiner ist als σ∞,
ist die elektrische Feldstärke E im Widerstand größer als in den
Stromzuführungen (σ∞).
Den
Faktor f = σ0/σ = Ex/E nenne ich für
diesen Text "Feldfaktor". Der Feldfaktor gibt an, wie sich
das elektrische Feld innerhalb der Übergangszone des Widerstand (
Ex ) gegenüber dem globalen Wert im Widerstand
(E) verändert.
In Bereichen, in denen er 1 ist, ist die Anpassung der elektrischen
Feldstärke an den globalen Wert im Widerstand vollzogen. Dann ist die
Feldstärke näherungsweise gleich der Feldstärke U/𝓁
(bei einer Länge 𝓁 des Widerstands und der
Spannung U am Widerstand). In Bereichen mit kleinerem Feldfaktor ist
auch die elektrische Feldstärke kleiner als U/𝓁,
wie etwa in den Stromzuführungen und in den Übergangszonen. Wird bei
einer festen Batteriespannung U die Leitfähigkeit des Widerstands
reduziert, entstehen zwischen den Übergangsstellen Zonen vergrößerter
Feldstärke. An ihrem Rand entstehen Raumladungen, die die elektrische
Feldstärke auf die im Widerstand herrschende anpassen. Der Feldfaktor
nähert sich jenseits der Stelle, wo σ0 /σ = 1/2 ist,
seinem Maximalwert 1. Je kleiner bei einem kontinuierlichen
Leitfähigkeitsübergang σ0 , desto tiefer liegt diese
Stelle im Bereich geringer Leitfähigkeit. Wenn der Feldfaktor 1
geworden ist, ist die Anpassung der Feldstärken innerhalb und
außerhalb des Widerstands vollzogen. Wegen der indirekten
Proportionalität zu σ verläuft Ex grundsätzlich anders als
σ. Dementsprechend liegt der Ladungsschwerpunkt der Raumladung
(modellbedingt) etwas (in der Regel um Bruchteile von wenigen
Atomlagen) in den Bereich geringer Leitfähigkeit verschoben, umso
weiter, je kleiner σ werden kann. Für die
Ladungsdichte ρ erhalten wir dann:
ρ = - (∂σ/∂x)
1/σ2·I/A · ε0 = - (∂σ/∂x)
1/σ2·U·σ0 /𝓁
· ε0 , also
ρ = - ∂σ/∂x
1/σ2·σ0 ·U/𝓁· ε0
|
und damit:
mit dem Leitfähigkeitsprofil s = - ∂σ/∂x
· 1/σ und dem Feldfaktor
f = σ0/σ = E/Ex
.
Aus ρ = - (∂σ/∂x)·1/σ2·I/A
· ε0
wird dann ρ = s·f· I/( σ0·A)
· ε0 (**).
Der Verlauf der Ladungsdichte ρ ist durch das Produkt von Leitfähigkeitsprofil
s = ∂σ/∂x
1/σ und Feldfaktor f = σ0/σ bestimmt.
Dieses Produkt als Maß für ρ (blau) wird in den folgenden Graphiken
dargestellt. Durch das quadratische Auftreten der Leitfähigkeit im
Nenner werden Zonen mit kleinem σ bevorzugt. Wiederum: Dort, wo sich
die Leitfähigkeit nicht ändert, verschwindet (bei
konstantem Querschnitt) das Leitfähigkeitsprofil s und damit
die Ladungsdichte ρ.
.
7. Es werden zwei verschiedene
Leitfähigkeitsmodelle für Gleichung (*) untersucht. Die
Rechnungen wurden in weiten Teilen analytisch durchgeführt und durch
numerische Rechnung mit einer Tabellenkalkulation überprüft.
In den Zeichnungen wurden meistens willkürliche Einheiten verwendet.
Während die Übergangszone eine Breite von wenigen Atomlagen hat, ist
der Abstand der zwei Übergangszonen sehr viel breiter als in der
Zeichnung. Da es nur auf die Verhältnisse der Ladungsdichten
ankommt, soll σ∞ (weit außerhalb des Widerstands) in
allen Fällen 1 sein. σ0 ist die
Leitfähigkeit im Widerstand.
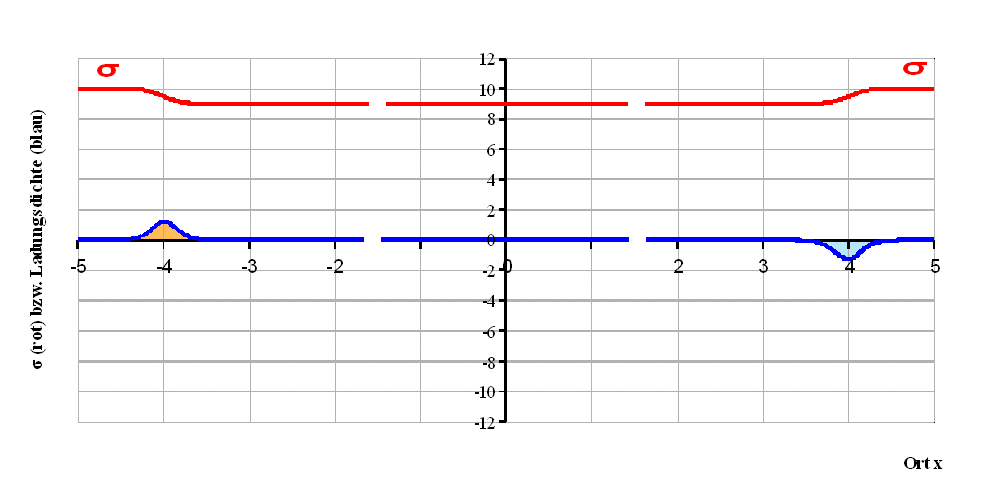 |
Abb. 2:
Ergebnis der Rechnungen für Leitfähigkeitsmodell
(2) mit kontinuierlicher
Änderung der Leitfähigkeit). Der schlechte Leiter
(Widerstand) beginnt bei x = -4 und endet bei x = 4.
Gezeichnet ist die 5-fache Leitfähigkeit σ (rot)
und die Ladungsdichte ρ (blau).
1/k = σ0/σ∞ = 0,9: σ verändert sich
bei +/- 4 von σ∞ = 1 auf
σ0 = 0,9 und umgekehrt. Der
geringen Leitfähigkeitsänderung entspricht eine geringe
Raumladung.
Man könnte sagen, dass hier die Raumladungen ein
Zusatzfeld "erzeugen", das das
vorhandene Feld zwischen ihnen verstärkt.
Außerhalb des Bereichs, in dem sich die Leitfähigkeit
(bei unveränderter Querschnittsfläche) ändert, gibt es
keine Raumladungen.
(Beachten Sie die Maßstabsänderungen auf der horizontalen
Ortsachse; stets willkürliche Einheiten.)
|
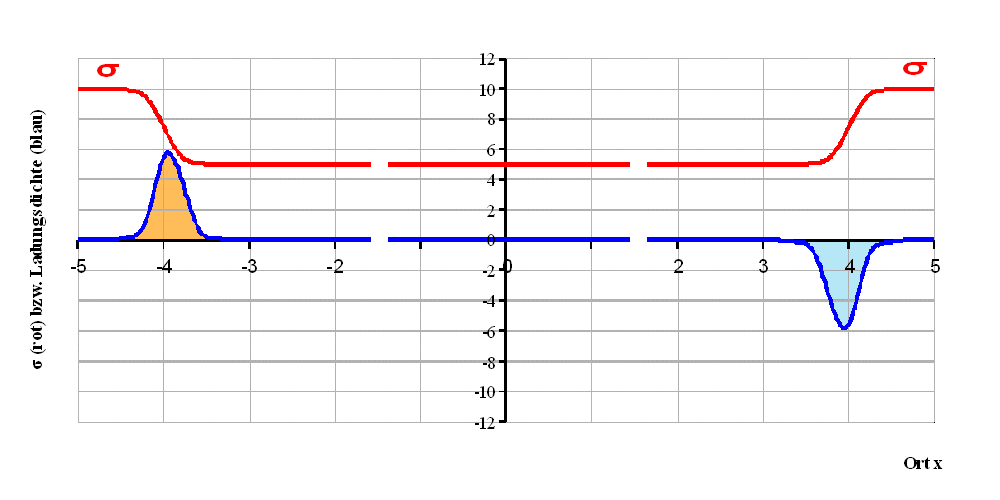 |
Abb. 3: Leitfähigkeitsmodell (2);
σ∞
= 1; σ0 = 0,5
Geringere Leitfähigkeit (rot) gehört zu größerem
elektrischen Widerstand und größerer elektrischer Feldstärke. |
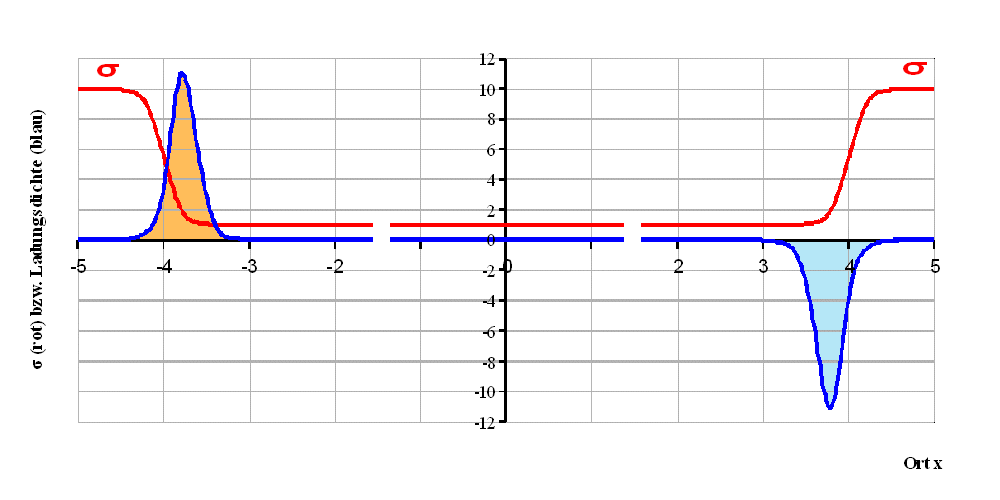 |
Abb. 4: Leitfähigkeitsmodell (2);
σ0 = 0,1.
Mit abnehmender Leitfähigkeit σ0 wächst der
Betrag der Raumladungen. Beide Raumladungen haben gleichen
Betrag, aber unterschiedliches Vorzeichen.
Das dazwischenliegende elektrische Feld muss noch mehr
verstärkt werden.
|
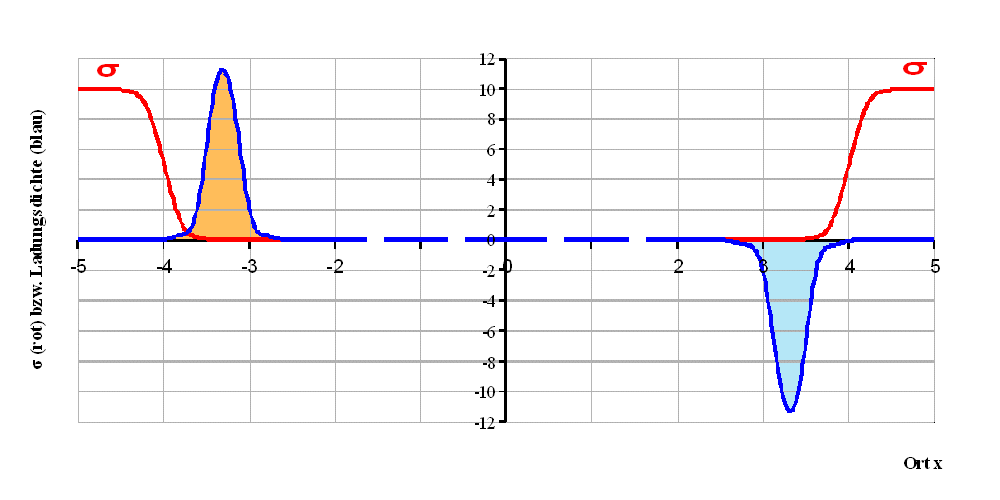 |
Abb. 5: Leitfähigkeitsmodell (2);
σ∞
= 1; σ0 = 0,01.
Die Raumladungen verändern sich jetzt nur noch wenig. Sie
wandern aber in das Innere des Widerstands hinein (wenn auch
nur um Bruchteile von wenigen Atomlagen).
(Dieses Leitfähigkeitsverhältnis entspricht etwa dem
Verhältnis von Cu-Leitungen und üblichen Widerstandsdrähten.
Beachten Sie wieder die Maßstabsänderungen auf der
horizontalen Ortsachse.)
|
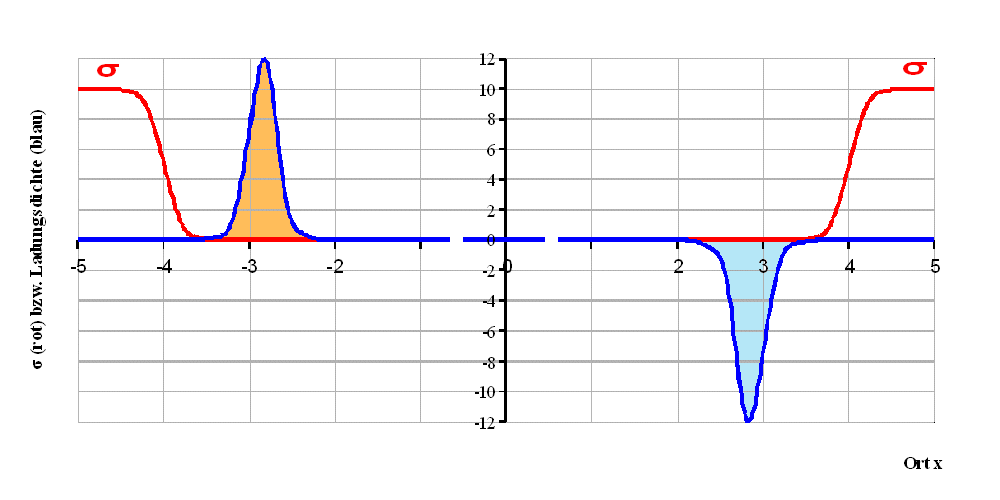 |
Abb. 6: Leitfähigkeitsmodell (2);
σ∞
= 1; σ0 = 0,0001
Beachten Sie - wie in allen diesen Zeichnungen - die
Maßstabsänderung auf der x-Achse: Der Abstand der
Übergangszonen ist sehr viel größer als deren Breite! |
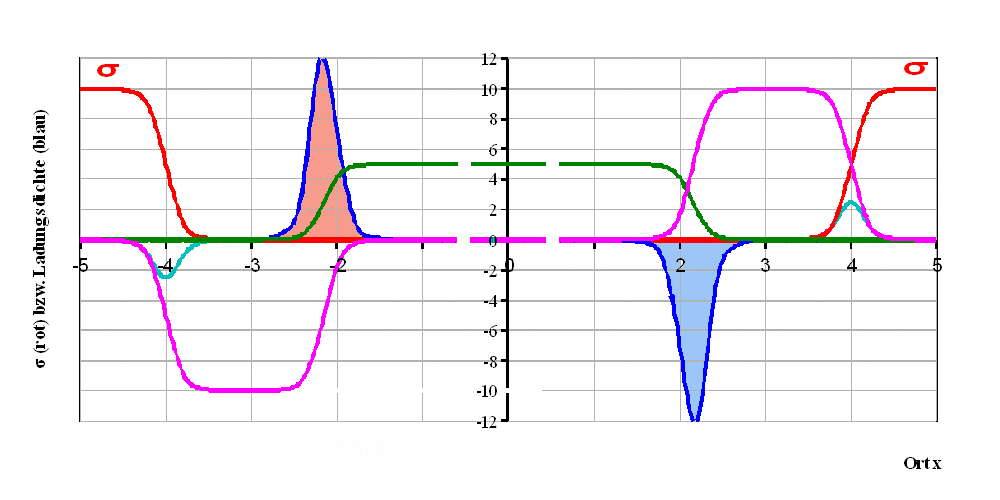 |
Abb. 7: Noch einmal Leitfähigkeitsmodell
(2); σ∞
= 1; σ0 = 0,00000001
Die magentafarbene Kurve stellt das
5-fache Leitfähigkeitsprofil s = ∂σ/∂x
/ σ dar. Durch σ im Nenner werden Anteile für sehr kleines σ
stark betont. Die grüne Kurve ist das 5-fache des Feldfaktors
f = σ0/σ . Fern von den Übergangszonen ist er 1,
nahe der Übergangszonen dagegen verändert er sich von σ0/σ∞
allmählich auf 1, indem σ auf σ0 abfällt. Der
Feldfaktor f bewirkt eine weitere Betonung der Bereiche sehr
kleinen σ's. ∂σ/∂x
(türkis) hat in der Flankenmitte (also hier bei +/- 4) sein
Extremum.
Das Leitfähigkeitsprofil (5-facher Wert: purpur) hat
breite Extrema mit den Werten von ca. +/- 2.
Die Verschiebung der Raumladungen (blau) zu
Bereichen kleiner Leitfähigkeit σ hin erfolgt in einem
Bereich von wenigen Atomlagen. Sie ist eher eine Folge des
Leitfähigkeitsansatzes von Modell 2.
|
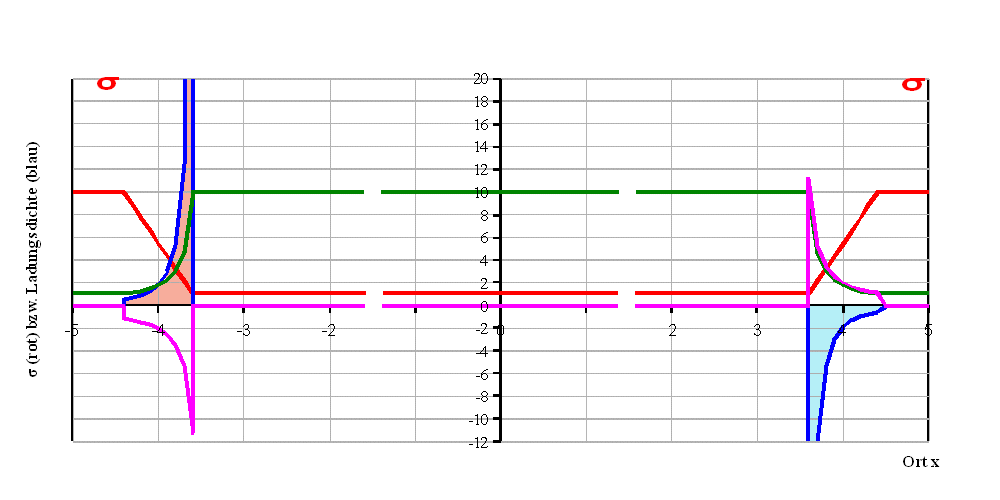 |
Abb. 4a: σ∞
= 1; σ0 = 0,1.
Leitfähigkeitsmodell (1):
Hier erfolgt ein linearer Übergang zwischen den
Leitfähigkeiten σ0 und σ∞ .
Das Leitfähigkeitsprofil (magenta) - ∂σ
/∂x 1/σ strebt bei einer Breite b
(hier 0,8) gegen (σ∞ - σ0)/(b·σ0)
am Rand kleiner Leitfähigkeit. Für σ0 => 0
divergiert dieser Faktor. (b = 0,8 gewählt)
Dagegen strebt für σ0 => 0 das Integral
gegen einen endlichen Wert (rötlich oder bläulich).
Feldfaktor (grün, 5-facher Wert): Die
Feldanpassung erfolgt vollständig in der Übergangszone, in
der sich σ verändert. Zwischen beiden Zonen gilt mit der
verwendeten Näherung E = U/𝓁.
Zwar divergiert die Ladungsdichte (blau) schwach
für jeweils einen Rand der Übergangszone, nicht aber die
jeweilige Gesamtladung, wie sich analytisch nachrechnen
lässt. Außerhalb der Übergangszone ist die Ladungsdichte
stets 0.
|
Leitfähigkeitsmodell 1:
Die Leitfähigkeit σ verändert sich in den Übergangszonen linear von
σ∞ auf σ0 bzw. umgekehrt. Die Ableitung
von σ und damit das Leitfähigkeitsprofil sind nur innerhalb der
Übergangszone von 0 verschieden und dort konstant. Innerhalb dieses
Bereichs muss die entstehende Ladungsdichte liegen. Die relativ hohe
elektrische Feldstärke zwischen beiden Übergangszonen muss durch die
Größe der Ladungsdichte angepasst werden. Mit abnehmender
Leitfähigkeit σ0 divergiert die Ladungsdichte an einem Rand
der Übergangszone schwach.
Es lässt sich aber durch analytische Rechnung zeigen: Das Integral
über das Leitfähigkeitsprofil für einen Übergang ist ohne
Berücksichtigung des Vorzeichens ln(σ0/σ∞), und
das Integral über die Ladungsdichte, also die Gesamtladung für einen
Übergang ist bis auf die Faktoren U/𝓁·ε0
gleich σ∞ - σ0. Während für σ0 gegen
0 das erste Integral divergiert, strebt die Gesamtladung gegen
den endlichen Wert σ∞ U/𝓁·ε0
, ein ganz vernünftiges Ergebnis (siehe Abb. 4a).
.
Leitfähigkeitsmodell 2:
Die Übergänge der Leitfähigkeit sollen jetzt gleichmäßiger erfolgen.
Dazu wird also für eine der beiden Übergangszonen angesetzt (für die
zweite entsprechend):
σ = σ0 + (σ∞ - σ0)/2·{1
+ tanh[-c(x+a)]} , wobei das Zentren der Übergangszone bei -a liegen
sollen. c soll ein Maß für die Breite der Übergangszone sein. Für x
=> -∞ strebt σ gegen σ∞ , für x => ∞ gegen σ0
Für die Ableitung erhalten wir dann:
∂σ /∂x = -(σ∞ -
σ0)/2·{1 - tanh2[-c(x+a)]}·k
∂σ /∂x = (σ∞ -
σ0)/2·{1 - tanh2[-c(-x+a)]}·c
Für x => -/+∞ strebt ∂σ /∂x
gegen 0.
Für die zweite Übergangszone gilt also:
σ = σ0 + (σ∞ - σ0)/2·{1
- tanh[-c(x-a)]} , wobei das Zentren der Übergangszone
bei +a liegen sollen. c soll ein Maß für die Breite der Übergangszone
sein. Für x => -∞ strebt σ gegen σ0
für x => ∞ gegen σ∞. Bei x = -a verändert sich die
Leitfähigkeit also von σ∞
auf σ0, bei x = a wiederum von
σ0 auf
σ∞.
Die Rechnung zeigt:
Je stärker die Leitfähigkeit reduziert wird, desto größer wird
zunächst die Raumladung. So hat man das erwartet. Aber mit abnehmender
Leitfähigkeit nähert sich die Ladungsmenge schließlich einem
Sättigungswert. Die Ladungsverteilung ändert sich schließlich kaum
mehr. Sie wandert von der Übergangszone geringfügig weg in das Medium
mit der geringeren Leitfähigkeit. Die elektrische Feldstärke steigt
erst hier weiter an. Die Gesamtladung für eine Übergangszone strebt
gegen einen endlichen Wert. Das Leitfähigkeitsprofil wird für σ gegen
0 immer breiter mit dem Integral - ln(σ∞/σ0).
Beide Leitfähigkeitsmodelle zeigen ähnliche Eigenschaften (Auftreten
von Raumladungen, Endlichkeit der jeweiligen Raumladung, Gesamtladung
mit Vorzeichen, Einfluss der Leitfähigkeitsunterschiede, Übergang zum
Isolator). Im Detail unterscheiden sie sich. Ein realistischeres
Modell wird möglicherweise zwischen den beiden untersuchten Modellen
liegen. Spätestens, wenn σ0 = 0, also bei vollständiger
Unterbrechung des Stromkreises, sollte wohl ein anderes Modell
verwendet werden, nämlich, dass die Batterie Ladungen auf einen
"Polklemmen-Kondensator" mit geänderter Kapazität pumpt.
Bei der Induktionsschleife ist das übrigens die
Situation (also der unterbrochene Stromkreis), in der aus der
Ringspannung durch die "Ladungsanhäufungen" eine gewöhnliche
Spannung gleicher Größe "zwischen den Enden der Schleife bzw. der
Spule" entstanden ist. Nur über diese Situation macht die
Schulphysik in der Regel Aussagen.
.
8. Zur Fragestellung nach der Rolle der
Raumladungen
Verringert man bei fester Batteriespannung U die
Leitfähigkeit im Widerstand, entstehen Raumladungen nahe der
Übergangszonen der Leitfähigkeit. Unabhängig von ihrem Vorzeichen
bleibt auch innerhalb des Widerstands wie im ganzen Stromkreis
außerhalb der Stromquelle die Tendenz "E-Feld außerhalb der
Batterie von + nach - gerichtet"
beibehalten. Ist die Leitfähigkeit des Widerstands quasi 0, sind die
Raumladungen von einem elektrischen Feld U/𝓁 in
der "Lücke" der Breite 𝓁 (Widerstand)
begleitet. In weiten Bereichen ist die Raumladung in einer
Übergangszone um so größer, je geringer die Leitfähigkeit im
Widerstand ist mit einem Sättigungswert für sehr kleine σ0.
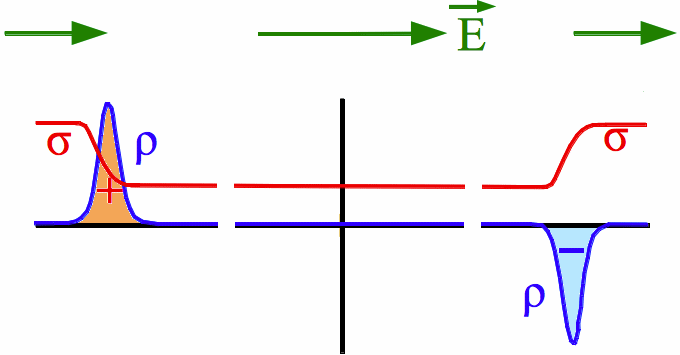
a) |
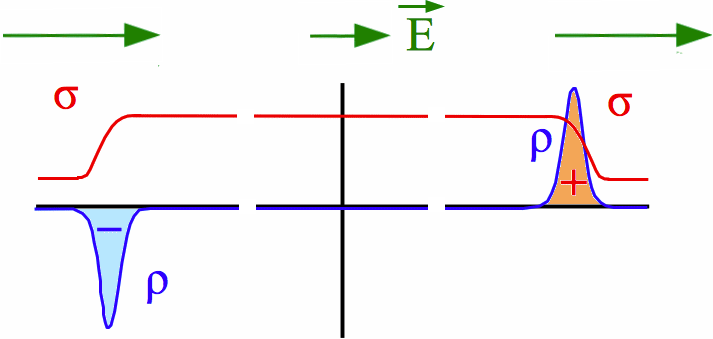
b)
|
Abb. 8a: Die Leitfähigkeit σ im
Widerstand ist kleiner als im Rest des Stromkreises. Die
Zeichnung zeigt die Polarität der Stirnladungen zur Anpassung
der elektrischen Feldstärke E. Im Widerstand ist die
elektrische Feldstärke größer (langer grüner Pfeil)
als im Rest des Stromkreises. Die Tendenz "E-Feld
außerhalb der Batterie von + nach - gerichtet"
wird beibehalten.
Abb. 8b: Die Leitfähigkeit σ im "Widerstand" ist hier größer
als im Rest des Stromkreises. Die Raumladungen zur Anpassung der
elektrischen Feldstärke E haben umgekehrtes Vorzeichen
als in Abb. 8a. Im "Widerstand" ist die elektrische Feldstärke kleiner
(kurzer grüner Pfeil) als im Rest des Stromkreises.
Die Tendenz "E-Feld außerhalb der
Batterie von + nach - gerichtet"
wird beibehalten trotz der "falschen" Polung der
Raumladungen in den Übergangszonen. Sie erzeugen ein
Zusatzfeld, das das äußere Feld schwächt und entgegengesetzt
zu diesem ist.
Das bestätigt erneut, dass die Raumladungen nur zur Anpassung
des elektrischen Felds dienen, nicht zur Erzeugung des
elektrischen Felds, das von der Batterie ausgeht.
(beide Zeichnungen schematisch)
|
| Bei einheitlichem Material (einheitliche Leitfähigkeit)
und einheitlichem Querschnitt gibt es im
geschlossenen Stromkreis nirgends Raumladungen. Erst, wenn
ein Widerstand in den Stromkreis geschaltet wird mit
unterschiedlicher Leitfähigkeit, entstehen an seinen
Enden Ladungsüberschüsse gleichen Betrags, aber
unterschiedlichen Vorzeichens. Durch sie wird der Betrag der
elektrischen Feldstärke E im Zwischenbereich
angepasst. Diese Raumladungen sind aber nicht
Ursache für das elektrische Feld, das den Stromfluss gemäß j
= σ·E begleitet und von der Batterie
ausgeht. |
Dass die Ursache für den Strom in der Batterie liegen
muss, ist anschaulich klar. Man sieht es auch daran, dass der Strom
unmittelbar zum Erliegen kommt, wenn die Batterie abgetrennt wird.
Dagegen kann man die Leitungen beliebig verformen, wobei sich das
elektrische Feld durch die sich verändernden Oberflächenladungen in
den Leitern immer wieder neu einstellt, ohne dass sich der Strom
verändert.
9. Einfluss von Querschnittsänderungen
Es soll jetzt ein Leiter untersucht werden, der bis zu einer
Übergangsstelle aus zwei parallel mit einander verbundenen Materialien
mit den Leitfähigkeiten σ und σ0 bestehe. Hinter der
Übergangsstelle bestehe er aus einheitlichem Material mit der
Leitfähigkeit σ. Wir können das auffassen als eine Reihenschaltung von
zwei Widerständen.
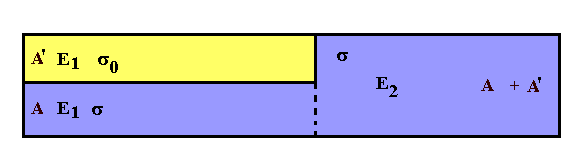 |
Abb. 9: Ein Leiter konstanter Querschnittsfläche A+A'
soll aus einer Reihenschaltung von zwei Widerständen bestehen,
wovon einer wiederum aus einer Parallelschaltung von zwei
Widerständen mit unterschiedlichen Leitfähigkeiten σ und σ0
und den Querschnittsflächen A und A' besteht.
Diese Prozedur wurde gewählt, weil man so die Rolle von
Querschnittsänderungen untersuchen kann, wenn man σ0
gegen 0 streben lässt.
|
Wegen der Wirbelfreiheit des elektrischen Felds herrscht in beiden
Teilen des Abschnitts 1 die gleiche elektrische Feldstärke, innerhalb
des Abschnitts 2 sowieso. Im Abschnitt 1 herrsche in beiden
Leitfähigkeitsbereichen mit den Querschnittsflächen A und A' die
Feldstärke E1, im Abschnitt 2 die Feldstärke E2.
Wegen der Konstanz der Stromstärke gilt
σ · E1·A + σ0· E1·A' = σ · E2·
( A1 + A' )
also
E1/E2 = σ · ( A + A' ) / ( σ · A +
σ0· A')
Wir wollen nun das Material mit σ0 zum Isolator
machen. Wenn σ0 = 0 also
Die Feldstärken verhalten sich umgekehrt wie die jeweiligen
Querschnittsflächen *). Diese Situation entspricht
einer Querschnittsänderung von A auf A + A' bei konstanter
Leitfähigkeit σ. Wieder wird die Feldstärkenänderung durch
Raumladungen nahe der Trennfläche zwischen beiden Bereichen erzeugt.
|
Raumladungen im Leiter entstehen auch,
wenn sich die Querschnittsfläche des Leiters ändert.
|
Im Extremfall, bei einer Unterbrechung des Leiters (σ0 =
0) von Abschnitt 6, entstehen tatsächlich Überschuss und Mangel von
Ladungen an den Unterbrechungsstellen ("Polen"). Ein direkter
Zusammenhang mit der Größe der Ladungen beim unverbundenen
Polklemmen-Kondensator ist nicht erkennbar. Die Kapazität des
Polklemmen-Kondensators wird verändert. Diese Ladungen passen die
elektrischen Feldstärken an das von Spannung und Länge der
Unterbrechungsstelle geforderte Maß an.
.
| 10. Zusammenfassung:
- Bei einem stationären Strom - wie in einem
Gleichstromkreis - ist der Stromfluss nicht die
Folge gegenseitiger Coulomb-Abstoßung von
Ladungsanhäufungen, sondern die Bewegung von im
Stromkreis vorhandenen Ladungen durch "äußere Kräfte"
(z.B. chemische "Kräfte" in der Batterie oder durch
Induktion).
- Ladungen nach dem Kondensator-Modell
nehmen nicht am Stromfluss teil. Es gibt keinen
physikalischen Anhaltspunkt dafür, dass die Batterie
nach Erreichen des stationären Zustands Ladungen auf den
Mantel pumpt oder von ihm absaugt.
- Ein Stromfluss ist demzufolge nicht die Folge
eines - wie auch immer definierten -
"Elektronendrucks" oder "elektrischen Drucks" als Folge
gegenseitiger Abstoßung von Ladungen. Modelle, die darauf
beruhen, sind m.E. abzulehnen.
- Ladungsanhäufungen im geschlossenen Stromkreis
treten nur auf bei Änderungen der Leitfähigkeit
oder des Leiterquerschnitts. Sie sind nicht
die Ursache von elektrischen Feldern, mit denen vorhandene
Ladungsträger durch den Stromkreis bewegt werden.
Sie passen vielmehr die elektrische Feldstärke an auf das
Maß, das durch Spannung, Widerstand, Stromstärke etc.
festgelegt ist.
- Solche Ladungsanhäufungen ("Oberflächenladungen", hier
"Stirnladungen" oder Raumladungen) treten nur nahe der
Übergangszonen (Änderungen der Leitfähigkeit oder
des Leiterquerschnitts) auf, nicht etwa generell im ganzen
Leiterabschnitt vor oder nach einem Widerstand. Das
widerspricht landläufigen Fehlvorstellungen zum einfachen
elektrischen Stromkreis.
- In den Stromzuführungen zwischen den Polen
der Batterie und einem Widerstand herrscht außerhalb der
Übergangszonen die gleiche Ladungsdichte ρ
= 0.
- Der Energietransport von der Energiequelle (Batterie) zu
einem Energie"verbraucher" wird vermittelt durch das vom
Strom erzeugte magnetische Feld und das elektrische Feld,
das von den statischen Oberflächenladungen
auf dem Mantel der Stromzuführungen
("Mantelladungen") ausgeht.
- Die Energie fließt außerhalb der Stromzuführungen, aber
überwiegend in ihrer Nähe, von der Energiequelle zum
"Verbraucher".
- Das Gerede von Überschuss und Mangel von Elektronen
am Minus- bzw. Pluspol bezieht sich auf statische
Oberflächenladungen ("Mantelladungen"),
die nicht am Stromfluss teilnehmen, aber eine wichtige
Funktion bei der Vermittlung des Energietransports
ausüben.
- "Mantelladungen" auf der Wandung der Leiter passen
das elektrische Feld an den Leiterverlauf an, nehmen
aber am Stromtransport nicht teil. Sie
entstanden ebenfalls in schwer zu überschauenden Vorgängen
während des
kurzzeitigen Einschaltvorgangs.
- Wenn beim Eintritt in einen Widerstand die
Leitfähigkeit in gleicher Weise absinkt wie sie beim
Austritt wieder ansteigt, unterscheiden sich die beiden
Raumladungen allein durch das Vorzeichen.
- Die vorstehenden Überlegungen machen keinen Gebrauch
davon, ob die Ursache des Stroms lokalisierte chemische
"Kräfte" in einer Batterie oder ausgedehnte sich ändernde
magnetische Felder in einer Induktionsschleife sind.
- Damit gibt es auch von dieser Seite her keinen
Anlass, Spannung und Stromstärke in beiden Fällen
unterschiedlich zu beschreiben und zu erklären, wie das
schon bei den Spannungsbegriffen Potenzialdifferenz und Ringspannung
war.
|
In diesem Licht sollten didaktische Versuche gesehen werden,
Spannung, Strom und elektrische Felder im Stromkreis für Schüler
plausibel zu machen. Die gegenwärtige didaktische Mode, Spannungen und
Feldstärken im Stromkreis durch Oberflächenladungen und Raumladungen
zu "erklären", entspricht nur teilweise den Sachverhalten und ist
außerdem für die Schule viel zu kompliziert. Natürlich haben auch die
Überlegungen dieses Textes in der Regel im Schulunterricht nichts zu
suchen. Ich bevorzuge die Argumentation eines für Schüler vorgesehenen
Textes student-stromkreis.html
oder nach dem Schülertext im Büchlein "Der
einfache elektrische Stromkreis - altes Wissen und neue Erkenntnis".
Definitionsfrage:
In der Physik kennt man nur eine Stromrichtung, die so genannte technische
Stromrichtung. Alle einschlägigen physikalischen Gesetze sind
auf sie bezogen. Dagegen gibt es auch noch Bewegungsrichtungen
der Ladungsträger, die je nach Ladungsvorzeichen mit der
Stromrichtung übereinstimmen oder entgegengesetzt sein können. Da
selbst in einem bestimmten Stromkreis unterschiedliche
Bewegungsrichtungen von positiven und negativen Ladungsträgern eine
Rolle spielen können, ist es nicht möglich und sinnvoll, eine Stromrichtung
durch
die Bewegungsrichtung zu definieren.
Die Elektrodynamik ist bekanntlich keine
kausale, sondern eine konsistente Theorie. Sie
beschreibt nicht Ursache und Wirkung, sondern gleichzeitig
vorliegende "Begleitumstände".
Unterschiedliche Feldstärken in
verschiedenen Raumbereichen deuten noch nicht auf Raumladungen hin
wie das Beispiel des inhomogenen Coulombfelds zeigt.
Dass hier das elektrische Feld der Leitergeometrie folgt, wird
mit Oberflächenladungen (Mantelladungen) erklärt. Lehrbücher der
Elektrodynamik beweisen das mit Hilfe der Wirbelfreiheit von E,
also mit rot E = 0 und der Kontinuitätsgleichung für den
Strom (div j = 0), wenn außerhalb des Leiters die
Leitfähigkeit σ = 0 ist, der Leiter also an einen Isolator
grenzt. Wie die hier diskutierten Raumladungen sind auch die
Oberflächenladungen nicht Ursache des elektrischen Stromes,
sondern passen das von der Batterie oder dem sich ändernden
Magnetfeld erzeugte elektrische Feld lediglich an die jeweilige
Leitergeometrie an. Statische Oberflächenladungen sind, wenn man
der Literatur glauben darf, sehr klein. Sie können auch nicht die
Energie für einen stationären Strom durch einen Widerstand
herbeischaffen.
Das lässt sich - Standardlehrbüchern der Elektrodynamik folgend -
mathematisch leicht zeigen:
(1) Wegen der Kontinuitätsgleichung gilt, wenn keine Ladungen
erzeugt werden (∂ρ/∂t = 0):
An der Grenzfläche: div j = div (σ·E)
= 0 . n sei ein Einheitsvektor, der auf einer
infinitesimalen Grenzfläche zwischen Leiter und Isolator senkrecht
steht. Gemäß den Regeln der Vektoranalysis gilt dann: div j
= n · (σ2·E2 - σ1·E1)
= 0. Dabei zeigt n von Gebiet 1 nach Gebiet 2. Wenn der
Leiter an einen Isolator angrenzt (Gebiet 2; σ2 = 0),
müssen also n und E1 aufeinander
senkrecht stehen: E im Leiter (Gebiet 1) ist parallel zur
Grenzfläche. Gäbe es im Inneren eine Feldkomponente senkrecht zur
Grenzfläche, würden durch sie Ladungen an die Grenzfläche zum
Isolator verschoben werden, bis sie verschwunden ist, bis also das
Feld parallel zur Grenzfläche verläuft.
(2) Im Inneren des Leiters: Weiter folgt aus der
Wirbelfreiheit von E im Bereich des Leiters: rot E
= 0 => n x (E2 - E1)
= 0 für einen infinitesimalen geschlossenen Weg, dessen eine
längere Seite in einem Gebiet 1 und dessen zweite längere Seite in
einem Gebiet 2 verläuft. Da beide Feldstärken bei angrenzendem
Isolator senkrecht zu n verlaufen, folgt daraus E2
- E1 = 0 bzw. E2 =
E1 . Insbesondere ergeben sich wegen (1) gleiche
elektrische Feldstärken über den ganzen Leiterquerschnitt. Am Rand
eines Leiters, der (mit scharfer Begrenzungsfläche) an einen
Isolator angrenzt, folgt, dass das E-Feld im Leiter
parallel zur Oberfläche gerichtet ist, und dass es außerhalb
zumindest gleiche Parallelkomponente hat.
(3) Wegen der konstanten Stromstärke im unverzweigten
Stromkreis und wegen des Ohm'schen Gesetzes j = σ·E folgt
bei konstantem Leiterquerschnitt und konstanter Leitfähigkeit,
dass j und E für sich überall konstanten
Betrag haben. Aus dem Ohm'schen Gesetzes j = σ·E folgt
bereits, dass sie im Leiterinneren überall gleichgerichtet sind,
also wie (1) schon sagt, dass sie der Leitergeometrie folgen.
*) Das würde auch aus der Konstanz der
Stromstärke folgen: Es gilt
σ· E1· A = σ· E2· (A+A'), also E1/E2
= (A+A')/A
Bei einer Polklemmen-Kapazität in
der Größenordnung von pF und Leitungskapazitäten von gleicher
Größenordnung und einer Spannung von 6 V werden ca. 10·10-12
As gespeichert. Bei einer Stromstärke von 0,1 A würde diese
Ladungsmenge in ca. 10-10 s abfließen. Dass die
gespeicherte Ladung so winzig ist, legt erneut nahe, dass ihr
Einfluss auf den Stromfluss vernachlässigbar ist.
Müller R., A semiquantitative
treatment of surface charges in DC circuits, Am. J. Phys. 80 (9),
September 2012 [http://dx.doi.org/10.1119/1.4731722]
.
( November 2015;
Mai 2018: einige Präzisierungen der Formulierung
September 2018: üblicher Beweis für dünne und scharf
begrenzte Leiter ergänzt
Januar 2019: Berechnung der Gesamtladung in einer
Raumladungszone ergänzt
Juli 2019: Zusammenhang zwischen Mantelladungsdichte und
Radialkomponente des elektrischen Felds außerhalb des
Leiters ergänzt
August 2019: auf Energietransport im Stromkreis
hingewiesen)