Eine naive Vorstellung des Gleichstromkreises behauptet, dass die den Strom transportierenden Ladungen eine potenzielle Energie haben, die von der Stromquelle in den Widerstand des Stromkreises transportiert wird, wo sie dann in Wärme umgesetzt wird. Dementsprechend wird vielfach angenommen, dass die Leitungselektronen "mit sich" die Energie im Leiter von der Stromquelle in den Widerstand transportieren. Auch andere Modelle des Stromkreises behaupten dies. Dass das nicht sein kann, sieht man schon daran, dass die durch einen Widerstand fließenden Ladungen in der Regel wegen ihrer geringen Fließgeschwindigkeit (typisch mm/s) in der Beobachtungszeit nicht aus der Stromquelle / Energiequelle gekommen sind und diese auch nie erreichen werden.

Die Elektrodynamik begründet den Energietransport *)  so: Gemäß des Poynting-Vektors (Energiestromdichte-Vektors) S =  1/μ0 E x B strömt die Energie dort, wo die elektrische Feldstärke E und die magnetische Feldstärke (magnetische Flussdichte) B gleichzeitig von 0 verschieden sind, wenn E und B nicht zueinander parallel sind. Im einfachen (unverzweigten) Stromkreis bei stromdurchflossenen Widerständen ist das leicht zu überschauen (Abb. 1a): E ist innerhalb des Widerstands in seiner Längsrichtung orientiert und seine Parallelkomponente ist in unmittelbarer Nähe des Widerstands stetig, B umgibt ringförmig die Stromdichte j = σ·E, E bzw. den Widerstand. E und B haben dort geeignete Richtungen. Wir beobachten: Bei einem stromdurchflossenen Widerstand strömt Energie gemäß S durch den Mantel von außen senkrecht zur Stromrichtung aus der Umgebung in den Widerstand hinein. Damit ist auch klar, dass unabhängig von der Stromrichtung, also auch bei Wechselstrom, der Energietransport immer von der Energiequelle zum Widerstand erfolgt.

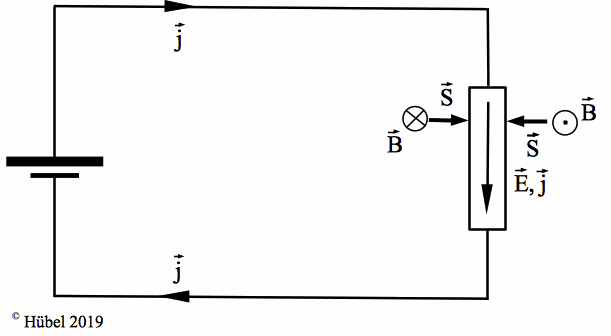
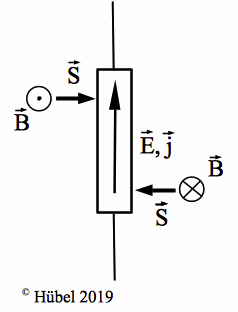
Abb. 1a: Nach Aussage des Energiestromdichte-Vektors S fließt Energie aus dem felddurchsetzten Vakuum in den Widerstand, und zwar durch seinen Mantel.   Abb. 1b, rechts: Energietransport mit umgekehrter Stromrichtung. Unabhängig von ihr strömt Energie in den Widerstand hinein. Die Abb. 1a und 1b erläutern auch den Energietransport durch einen Wechselstrom: Strom, elektrisches und magnetisches Feld ändern ständig ihre Richtungen. Der Energietransport längs S ist dennoch immer aus dem Raum in den Widerstand hinein gerichtet. Es wird elektromagnetische Energie transportiert.

Wie kommt aber die Energie von der Energiequelle (Stromquelle) zum Widerstand?   (1) Nehmen Sie an, dass die Stromzuführungen zum Widerstand widerstandslos sind (Leitfähigkeit σ => ∞, spezifischer Widerstand = 0). Wegen E = j/σ ist das Innere der Stromzuführungen frei von elektrischem Feld.  Senkrecht auf dem Mantel könnten allerdings - in schulischer Sprechweise - E-Feldlinien in Oberflächenladungen münden. Das sind also die statischen Ladungen, die auf dem Polklemmen-Kondensator nach Einstellen des stationären Stroms übrig geblieben sind. Besonders in der Umgebung der Stromzuführungen haben wir also gemeinsam ein statisches elektrisches Feld (als Folge dieser Oberflächenladungen) und ein magnetisches Feld, das den Strom ringförmig umgibt. Abb. 2  zeigt, dass sich daraus Energiestromdichte-Vektoren S ergeben, die von der Energiequelle zum Widerstand zeigen.

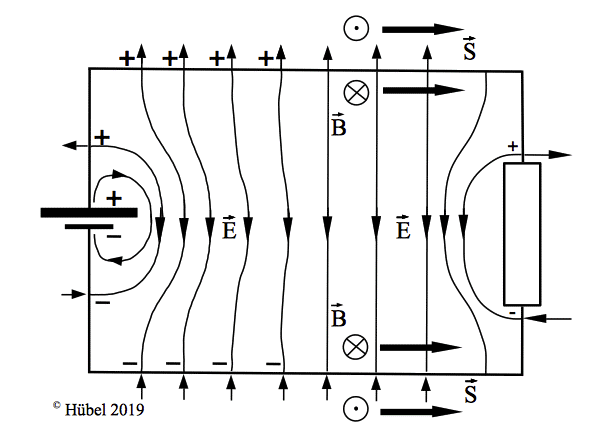
Abb. 2: Der Energiestromdichte-Vektor S führt von der Energiequelle zum Widerstand, außerhalb des Leiters, aber vor allem in seiner Nähe, innerhalb und außerhalb der Leiterschleife. Hier werden widerstandslose Stromzuführungen zum Widerstand angenommen. Deshalb münden die elektrischen Feldlinien senkrecht auf der Wandung der Leitungen. (2) Die Energie wird nicht in den Leitern transportiert; die fließenden Ladungen vermitteln nur den Transport der Energie. Sie erzeugen ein Magnetfeld, das zusammen mit dem elektrischen Feld statischer Oberflächenladungen auf den Stromzuführungen den Energietransport längs S vermittelt, unabhängig von der Stromrichtung.

(3) Solche Oberflächenladungen sind statisch und nehmen nicht am Stromfluss teil. Sie können selbst keine Energie liefern. Diese kommt ganz aus der Energiequelle / Stromquelle. Der Energietransport hängt nur sehr indirekt mit den fließenden Ladungen zusammen. In der Regel werden diese ohnehin nie die Energiequelle erreichen oder aus ihr kommen. Es werden offenbar beide Leitungen (Hin- und Rückleitung für den Strom) benötigt, um die Energie in ihrer Umgebung zum Widerstand zu transportieren. Dementsprechend sind didaktische Modelle zu beurteilen, die den Energietransport an die Bewegung der Ladungen binden, bei denen die Ladungen die Energie "mit sich" transportieren sollen (z.B. auf dem Transport von potenzieller Energie beruhende Modelle, "Rucksack-Modell", "Bienen-Nektar-Modell").

Weil das Magnetfeld in Leiternähe am größten ist, ist S dort auch am größten:

So ist also das Innere der Stromzuführungen zwischen den Polklemmen und den Anschlüssen des Widerstands elektrisch neutral; es gibt dort keine Raumladungen, wenn sich die Leitfähigkeit nicht ändert. Dagegen sind dort statische Oberflächenladungen auf dem Mantel notwendig für den Energietransport. Sie nehmen nicht am Stromfluss teil (die freibeweglichen Leitungselektronen bzw. der Strom fließen im Leiter), haben aber die wichtige Funktion,  zusammen mit dem vom Strom erzeugten Magnetfeld, den Energietransport von der Energiequelle zum Energie"verbraucher" zu vermitteln. Die Energie kommt ganz klar aus der Energiequelle (Stromquelle). Die Oberflächenladungen können keine Energie liefern, weil das von ihnen erzeugte elektrische Feld ein Potenzialfeld ist, für das Energieerhaltung gilt (vgl. "Wegunabhängigkeit").

Bei endlicher Leitfähigkeit in den Stromzuführungen münden E-Feldlinien nicht mehr senkrecht auf der Leiteroberfläche. Es herrscht in ihnen auch ein paralleles elektrisches Feld. Längs des zugehörigen Poynting-Vektors strömt also auch Energie in diesen Leiter. Wesentlich für den Energietransport zum Energie"verbraucher" ist dagegen wie oben die senkrecht auftreffende Komponente des elektrischen Felds.

Energietransport in den Widerstand bei der Induktion

Zwar macht das Induktionsgesetz keine Aussage über die Verteilung des elektrischen Wirbelfelds E längs einer Induktionsschleife, aber zusammen mit dem Ohm'schen Gesetz j = σ·E folgt, dass in widerstandslosen Abschnitten mit σ => ∞ (spezifischer Widerstand = 0) keine elektrische Feldstärke im Leiter herrschen kann. Die durch Induktion entstehende elektrische Wirbel-Feldstärke E verteilt sich dann ganz auf Abschnitte mit endlicher Leitfähigkeit σ, also in bzw. längs eines Widerstands R. Zur Beurteilung des Energiestroms in solche Widerstände muss auch die vom Induktionsstrom I mit der Stromdichte j hervorgerufene magnetische Feldstärke B_I herangezogen werden. Hier wird eine eher qualitative Erklärung nahe Schulniveau versucht.

In die Induktionsschleife sei ein Widerstand R eingebaut, alle sonstigen Leiter sollen widerstandslos sein. Die gesamte Ringspannung fällt dann am Widerstand ab. Die elektrische Feldstärke E ist in seinem Inneren parallel zu ihm gerichtet, gleichgerichtet mit der Stromdichte j; auch außerhalb gibt es eine parallele Komponente. Außerdem entsteht ein magnetisches Feld BI gemäß der rechten Faustregel, das den Widerstand ringförmig umgibt. Die Abb. 3 zeigt den Energiestrom, der gemäß S zu beiden Seiten in den Widerstand hinein fließt, senkrecht zu dessen Mantel. Die Energie kommt in diesem Fall aus dem sich ändernden Magnetfeld B (nicht BI), vermittelt durch das elektrische Wirbelfeld E bzw. den folgenden Induktionsstrom mit der Stromdichte j und so also auch durch BI). Das wird im Folgenden genauer erläutert.

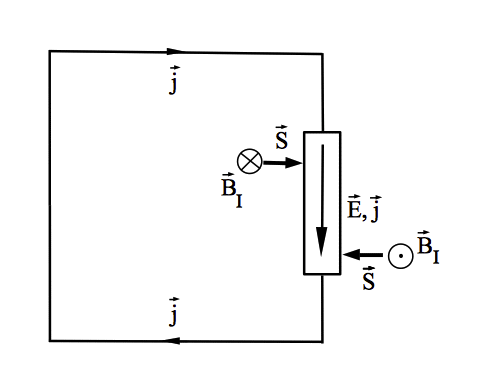
Abb. 3: Das Magnetfeld BI, das der Induktionsstrom erzeugt, vermittelt zusammen mit dem induzierten elektrischen Feld E einen Energiestrom in den Widerstand hinein.

Energietransport bei der Induktion mit der Lenz'schen Regel erklärt

Betrachten Sie eine Leiterschleife, die einen sich zeitlich ändernden magnetischen Fluss mit der Flussdichte B(t) einschließt. Die Leiterschleife soll homogen mit einem leitfähigen Material der konstanten Leitfähigkeit σ belegt sein. Es geht darum, die Richtung des Energiestromdichte-Vektors S in verschiedenen Situation zu überlegen.

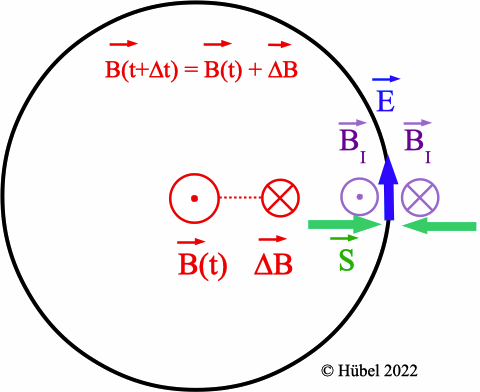
Abb. 4:  Zu einem beliebigen Zeitpunkt t sei die momentane magnetische Flussdichte B(t). Betrachte jetzt B(t + Δt), also die magnetische Flussdichte einen kleinen Zeitabschnitt Δt später (t + Δt). In diesem Zeitabschnitt soll sich B um ΔB ändern mit dem Ergebnis                 B(t+Δt) = B(t) + ΔB In der Zeichnung links zeigt die magnetische Flussdichte B(t) aus der Zeichenebene heraus. Der Betrag von B soll hier abnehmen; deswegen haben B(t) und ΔB entgegengesetzte Richtungen. Nach der Lenz'schen Regel erfolgt die Induktion so, dass der Änderung von B, also ΔB (rot), entgegengewirkt wird. Der Induktionsstrom bzw. die induzierte elektrische Feldstärke E (blauer Pfeil) ist dann so gerichtet, dass das durch die Induktion entstehende Magnetfeld BI (gemäß der rechten Faustregel) innerhalb der Leiterschleife der Änderung ΔB entgegen wirkt (violett). Das Kreuzprodukt E x BI bzw. der Energiestromdichte-Vektor S haben dann die grün gezeichneten Richtungen. Gleiches gilt für alle übrigen Positionen längs der Leiterschleife: vermittelt durch das "induzierte" Magnetfeld BI fließt Energie aus dem sich ändernden Magnetfeld B in den Widerstand der Leiterschleife.

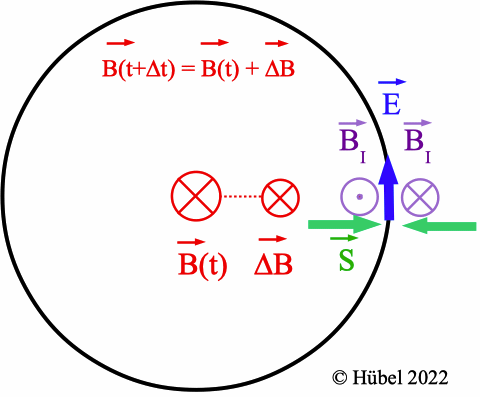
Abb. 5: Die magnetische Flussdichte B(t) zeigt hier in die Zeichenebene hinein. Der Betrag von B soll hier zunehmen; deswegen haben B(t) und ΔB gleiche Richtungen. Durch Induktion entsteht ein Magnetfeld BI, so dass sich im Inneren der Leiterschleife ΔB und BI ganz oder teilweise gegenseitig aufheben. S behält seine Richtung bei: Energie strömt in den Widerstand hinein (grün).

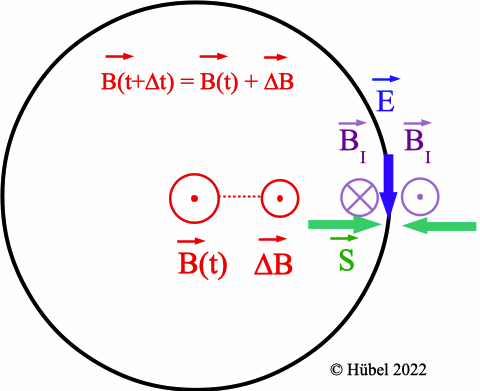
Abb. 6: Die magnetische Flussdichte B(t) zeigt hier aus der Zeichenebene heraus. Der Betrag von B soll hier zunehmen; deswegen haben B(t) und ΔB gleiche Richtungen. Durch Induktion entsteht ein Magnetfeld BI, so dass sich im Inneren der Leiterschleife ΔB und BI ganz oder teilweise gegenseitig aufheben.

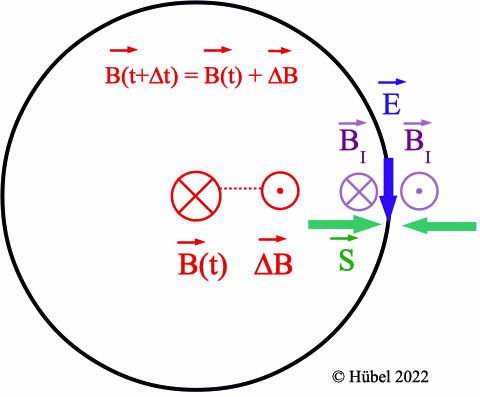
Abb. 7: Die magnetische Flussdichte B(t) zeigt hier in die Zeichenebene hinein. Der Betrag von B soll hier abnehmen; deswegen haben B(t) und ΔB entgegengesetzte Richtungen.

In allen 4 Situationen strömt Energie (grün) aus dem sich ändernden Magnetfeld B(t) in den Widerstand der Leiterschleife. Das gilt demnach auch dann, wenn ein magnetisches Wechselfeld B(t) vorliegt, wenn also der Induktionsstrom als Wechselstrom entsteht.

Literatur

Diskussion des Poynting-Vektors:

Vgl. Galili, I., Goihbarg E., Energy transfer in electrical circuits: A qualitative account, Am. J. Phys. 73 (2), Febr. 2005, S. 141 - 144

In a simple circuit, where does the energy flow? A collection of diagrams, 2000,  William Beaty BSEE, http://amasci.com/elect/poynt/poynt.html

^*) Es gibt Situationen, in denen man mit einer lokalen Auffassung von S sehr vorsichtig sein muss. Z.B. bei statischen Feldern in der Nähe eines Widerstands scheint S einen Energiestrom in den Widerstand hinein anzudeuten, und an anderen Stellen wieder heraus, aber so, dass insgesamt weder Energie in den Widerstand hinein noch heraus fließt, wie das auch zu erwarten war.