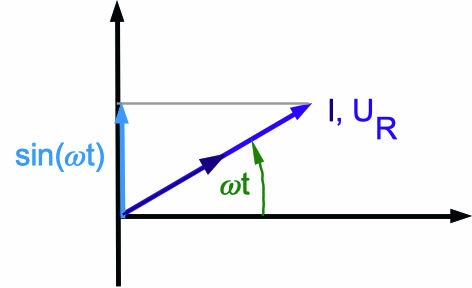
Abb. 1: Allein Ohm'scher Widerstand R in einem
Wechselstromkreis:
Strom I und Spannung UR (bzw. die äußere angelegte
Spannung U) im Zeigerdiagramm.
|
SG151 Serielle Wechselstromkreise © H. Hübel Würzburg 2013 |
Impres-sum |
I Worum geht es bei Wechselstromkreisen?
An verschiedene in Reihe geschaltete Bauteile soll eine Wechselspannung
U(t) angelegt werden (Ohm'scher Widerstand, Kondensator, Spule). Dass auch
ein Kondensator einen Strom durchlässt,
dürfte dir mittlerweile bekannt sein. Wenn die Bauteile hintereinander (in
Reihe oder in Serie) geschaltet sind, fließt durch alle Bauteile der
gleiche Strom. Zunächst ist eine Frage, welchen Zeitverlauf die
Stromstärke bei einem bestimmten Zeitverlauf der Spannung hat. Die Frage
lässt sich nur in Sonderfällen einfach beantworten, für die Praxis sind
sinusförmige Verläufe besonders wichtig. Dann ist noch zu klären, ob sich
so etwas wie ein Wechselstrom-Widerstand definieren lässt, und welche
Frequenzabhängigkeit er ggf. hat. Er ist in der Regel nicht konstant wie
ein Ohm'scher Widerstand. Damit kannst du dann einfach erklären, wie sich
der Strom und die Spannungsabfälle an den Bauteilen mit zunehmender
Frequenz verändern.
II Allein Ohm'scher Widerstand im Stromkreis
Wegen des Ohm'schen Gesetzes U = R·I sind U und I immer proportional zueinander. U und I hängen dann in gleicher Weise von der Zeit ab, sie sind z.B. proportional zu sin(ω·t). Zu den Zeiten, zu denen I verschwindet, ist auch U = 0. Zu den Zeiten, zu denen I maximal ist, ist auch U maximal. I und U erreichen auch gleichzeitig ihr Minimum. Man sagt: "I und U sind gleichphasig" (oder "in Phase"). Der Widerstand ist unabhängig von der Frequenz f oder Kreisfrequenz ω·t = 2π ·f des Wechselstroms.
U(t) und I(t) sind zu allen Zeitpunkten t proportional zueinander, und bei einem sinusförmigen Wechselstrom auch proportional zu sin(ω·t).
Das wird üblicherweise in einem Zeigerdiagramm dargestellt. Ein
Zeiger konstanter Länge I0 bzw. U0 [Maximal- oder
Scheitelwerte von I(t) und U(t)] rotiert dabei in einem rechtwinkligen
Koordinatensystem um den Koordinatenursprung im Gegenuhrzeigersinn. I0
bzw. U0 werden auch Amplituden genannt, Stromamplitude und
Spannungsamplitude.
Der Drehwinkel (grün) - gemessen gegenüber der horizontalen Achse -
entspricht ω·t. Wenn sich ω·t verändert, wandert die Spitze der Zeiger auf
einem Kreis mit dem Radius I0 bzw. U0 um den
Koordinatenursprung. Die Projektion des Zeigers auf die vertikale Achse
ist dann jeweils I0·sin(ω·t) bzw. U0·sin(ω·t).
Man kann so zu allen Zeitpunkten I(t) und U(t) veranschaulichen. Z.B.:
Wenn ω·t = π/2, sind I(t) und U(t) maximal, wenn ω·t = π oder = 0,
verschwinden I(t) und U(t).
Wesentlich ist die Spannungsbilanz: Die von außen angelegte Spannung U(t) ist gleich der Summe aller Spannungsabfälle an den Bauteilen.
|
|
Abb. 1: Allein Ohm'scher Widerstand R in einem
Wechselstromkreis: |
Der Innenwiderstand der Stromquelle (ihr Ausgangswiderstand) sollte
sich für die folgenden Diskussionen möglichst wenig bemerkbar machen.
Bei Experimenten unter Verwendung eines Funktionsgenerators sollte
deshalb dessen Leistungsausgang angeschlossen werden. Aber wegen der
Selbstinduktion Vorsicht bei Anschluss oder Abtrennen einer Spule!
IV Allein Kondensator im Stromkreis
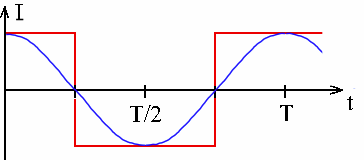
2.a) Wenn ein abschnittsweise konstanter Strom mit wechselndem Vorzeichen durch einen idealen Kondensator geschickt wird, entsteht an der Spule eine abschnittsweise linear wachsende oder fallende Spannung U entsprechend Abb. 1, weil es eine gewisse Zeit dauert, bis der konstante Strom den Kondensator geladen oder entladen hat, bis sich eine bestimmte Ladespannung auf- oder abgebaut hat.
|
|
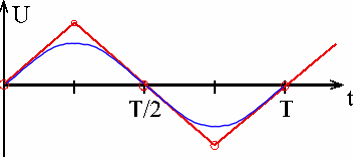
Abb. 2: Allein Kondensator im Wechselstromkreis Abschnittsweise konstanter Strom I sorgt für linear veränderliche Spannung U. links: dreiecksförmige Spannung, rechts: sinusförmige Spannung zeichnerisch ergänzt |
  |
Folgerungen:
1. Es muss erst ein Strom eine Zeit lang fließen, damit sich nach und nach eine Spannung am Kondensator ausbilden kann.
2. Die Steigung der Spannung entspricht der Stromstärke: Wächst die Spannung am Kondensator, dann hat die Stromstärke positives Vorzeichen, fällt die Spannung, hat die Stromstärke negatives Vorzeichen.
3. Je schneller sich die Spannung verändert, desto größer muss der Betrag der Stromstärke sein.
4. Der gleiche Zusammenhang zwischen der Steigung der Spannung und der Stromstärke gilt, wenn ein sinusförmiger (Abb. 2, rechts) Strom durch den Kondensator geschickt wird. Wenn U(t) prop. zu sin(ω·t), ist I(t) prop. zu cos(ω·t). Beim Kondensator "eilt die Stromstärke der Spannung voraus", weil erst ein Strom fließen muss, damit sich nach und nach eine Spannung ausbilden kann.
|
cosinusförmiger Strom => sinusförmige Spannung UC |
Variante:
1.a) Linear wachsende und fallende Spannung am Kondensator hat konstant positiven oder konstant negativen Strom zur Folge. Die Stromstärke entspricht gemäß I = C dU/dt der Steigung der Spannung.
1.b) Sinusförmige Spannung am Kondensator [U = U 0 sin(ω·t)] hat entsprechend einen Strom zur Folge, der gemäß I = C dU/dt = - C·U0·ω·cos(ω·t) der Steigung der Spannung entspricht.
Strom und Spannung sind nicht mehr in Phase. Sie erreichen zu verschiedenen Zeiten ihr Maximum oder auch ihr Minimum. Das entspricht einem phasenverschobenen Zeitverlauf. Merkwürdigerweise ist die Stromstärke gerade dann maximal, wenn die Spannung verschwindet! Für die Beträge gilt: | I | = I0 = ω·C·U0 . Die Beträge von I und U, also I0 bzw. U0, sind wie im Gleichstromfall zueinander proportional. Wir müssen aber die Phasenverschiebung berücksichtigen.
Damit wird der Betrag eines Wechselstrom-Widerstands des Kondensators definiert.
ZC = U0 /I 0 = 1/(ω·C)
(Etwas allgemeiner verwendet man Effektivwerte zur Definition eines Wechselstrom-Widerstands: ZC = Ueff /Ieff. Bei sinusförmiger Zeitabhängigkeit von Strom und Spannung unterscheiden sich Effektiv- und Maximalwerte nur um einen konstanten Faktor: Ueff = U0/√2, Ieff =I0/√2. In einem solchen Fall kannst du Effektivwerte und Maximalwerte gegeneinander austauschen.)
Mit zunehmender Kreisfrequenz ω und Kapazität C sinkt der Wechselstrom-Widerstand des Kondensators. Schlampig formuliert sagt man auch manchmal, dass bei einer gegebenen Maximalspannung U0 ein Kondensator einen umso größeren Strom durchlässt, je größer die Kreisfrequenz ω und die Kapazität C sind.
|
|
Abb. 3: Das ist besonders einsichtig, wenn man die Rotation der Zeiger von I und UC im Gegenuhrzeigersinn betrachtet. Die von außen angelegte Spannung U(t) ist die vektorielle Summe von UR und UC: U(t) = UR + UC (Spannungsbilanz; hier UR = 0). Durch die vektorielle Summe werden die unterschiedlichen Zeitabhängigkeiten beider Spannungen berücksichtigt. |
V Allein ideale Spule im Stromkreis
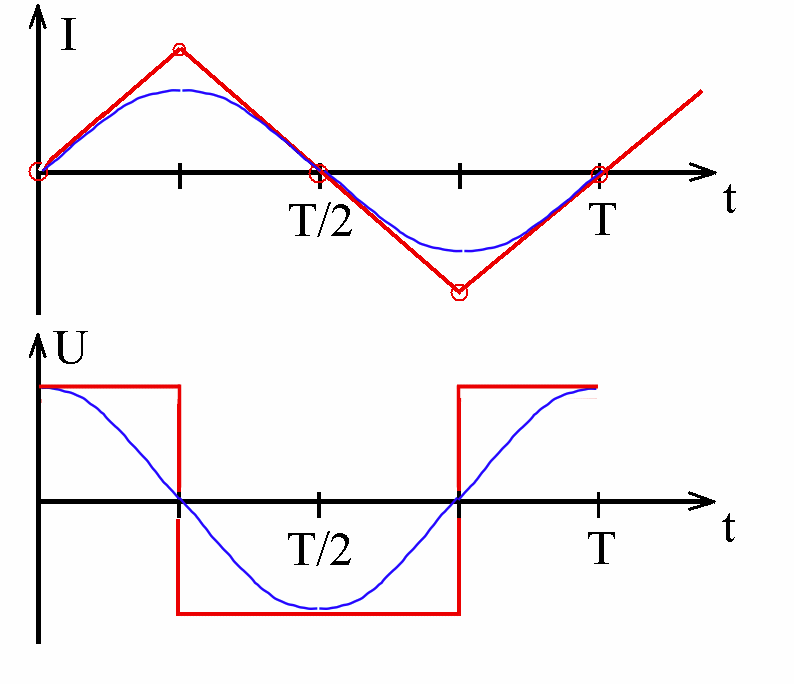
2.a) Wenn ein abschnittsweise linear wachsender und linear fallender Strom (ein Dreiecksstrom) durch eine Spule mit möglichst geringem Widerstand (eine "ideale" Spule) gepumpt wird*), wird in ihr eine abschnittweise konstante Spannung nach Abb. 4 induziert, eine Selbstinduktionsspannung Uind. Sie ist proportional zur Steigung der Stromstärke. Die Folge von Uind ist ein entgegengesetzter Spannungsabfall UL [U prop dI/dt].
Zum Unterschied von Uind
und UL (Uind = - UL).
|
|
Abb. 4: Schickt man einen dreiecksförmigen Strom (oben) durch eine weitgehend widerstandslose Spule, erzeugt diese eine abschnittsweise konstante Selbstinduktionsspannung Uind bzw. einen Spannungsabfall UL = - Uind (unten).*)
Wie sich Stromstärke und Spannungen mit der Zeit verändern, wird
durch ein Zeigerdiagramm beschrieben (Abb. 5) |
 |
2.b) Wird ein sinusförmiger Strom durch eine ideale Spule geschickt, entsteht eine Selbstinduktionsspannung, die gemäß [U = - L · dI/dt] proportional zur Zeitableitung der Stromstärke ist. Wenn I = I0·sin(ω·t) ergibt sich U = - L·ω·I0·cos(ω·t) = - U0·cos(ω·t) , wobei U0 = L·ω·I0 . Damit definieren wir wieder einen Wechselstrom-Widerstand der Spule mit
ZL = U0/I0 = ω·L .
Auch bei der Spule erreichen Stromstärke und Spannung zu unterschiedlichen Zeiten ihr Maximum oder auch ihr Minimum. Merkwürdigerweise ist die Stromstärke wieder gerade dann maximal, wenn die Spannung verschwindet! Strom und Spannung sind gegeneinander phasenverschoben.
Folgerungen:
ein linear veränderlicher Strom hat eine konstante Selbstinduktionsspannung zur Folge,
|
sinusförmige Stromstärke => cosinusförmige Spannung UL |
|
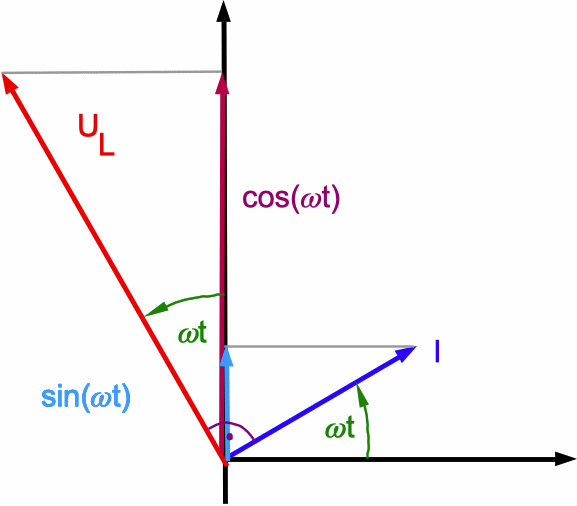 |
Abb. 5: Das ist besonders einsichtig, wenn man die Rotation der Zeiger von I und UL im Gegenuhrzeigersinn betrachtet. Die von außen angelegte Spannung U(t) ist die vektorielle Summe
von UR und UL: U(t) = UR + UL (Spannungsbilanz; hier UR = 0). |
Folgerungen:
1. Bei der Spule "eilt die Spannung der Stromstärke voraus", weil sich
erst ein Strom ändern muss, damit sich eine Induktionsspannung ausbilden
kann.
2. Die Spannung ist proportional zur Steigung der Stromstärke.
3. Je schneller sich die Stromstärke verändert, desto größer ist der Betrag der Selbstinduktionsspannung Uind bzw. des Spannungsabfalls UL.
VI Stromkreis mit idealer Spule und Kondensator
Der Widerstand sei R = 0, die Induktivität der Spule L, die Kapazität des Kondensators C.
|
|
Abb. 4: Dann eilt die äußere Spannung U(t) der Stromstärke I voraus. Bei der Rotation verändern sich sin(ω·t) und cos(ω·t) und die jeweiligen Komponenten in Richtung der vertikalen Achse. Bei einer anderen Kreisfrequenz ω überwiegt UC gegenüber der Spannung UL. Dann ist U(t) gleichgerichtet mit UC und die Stromstärke I eilt der Spannung U(t) voraus. |
Es gibt auch eine Frequenz, bei der sich beide Spannungen in dieser Näherung (R = 0) zur theoretischen Gesamtspannung 0 addieren. Das ist eine Art von Resonanz. Die Spannung U(t) = 0 (zu allen Zeiten) ergibt sich, wenn UC0 = UL0 bzw. ZC·I0 = ZL·I0 bzw. ZC = ZL , also 1/(ω·C) = ω·L . Die Frequenz, bei der das geschieht, heißt Resonanzfrequenz
ω0 = 1/√(L·C).
Merkwürdigerweise wird dann nur eine verschwindend kleine Spannung U(t) benötigt, um einen endlichen Strom durch die Reihenschaltung von idealer Spule und Kondensator zu treiben.
VII Stromkreis mit einer Reihenschaltung von Ohm'schem Widerstand R, Kondensator mit Kapazität C und Spule mit Induktivität L
Während beim Ohm'schen Widerstand der Wechselstrom-Widerstand
frequenzunabhängig ist, wächst er bei der Spule mit der Frequenz, und
nimmt er beim Kondensator ab. Sind z.B. Spule und Kondensator
hintereinander (in Reihe oder Serie) geschaltet, so verhalten sich beide
Wechselstromwiderstände unterschiedlich mit der Frequenz. Dementsprechend
verändern sich die Spannungsabfälle bei einem festen Maximalwert der
Stromstärke (ihrer Amplitude), obwohl durch alle in Reihe geschalteten
Bauteil derselbe Strom fließen muss. Das hat Konsequenzen für die Größe
des gemeinsamen Stroms, weil die Summe aller Spannungsabfälle gleich der
von außen angelegten Spannung sein muss.
Bei mehreren Bauteilen im Stromkreis nennen wir die Spannungsabfälle UR, UC und UL. Bei in Reihe (Serie) geschalteten Bauteilen fließt durch alle derselbe Strom I(t). Es ist deshalb sinnvoll, die Zeitabhängigkeiten der Spannungen des Zeigerdiagramms auf I zu beziehen.
Sind in einem Wechselstromkreis Ohm'scher Widerstand R, Kondensator mit Kapazität C und Spule mit Induktivität L hintereinander geschaltet, ist die wechselnde Betriebsspannung U = U(t) gleich der Summe der Spannungsabfälle UR, UC und UL. Der Widerstand R kann auch den Innenwiderstand Ri der Spule enthalten.
Es gilt dann die Spannungsbilanz:
|
(Gl. *) U = UR + UC + UL , wobei UR = R·I, dUC /dt = 1/C · I und UL = L · dI/dt. |
Wenn I prop. zu sin(ω·t), ist auch UR prop. zu sin(ω·t), ebenso wie dUC /dt. UC ist dann prop. zu - cos(ω·t) und UL prop. zu cos(ω·t).
|
|
Abb. 3: Zeigerdiagramm für Wechselstromkreis mit R, C und
L (Reihenschaltung): Der Zeitverlauf der Stromstärke und der
Spannungen wird durch rotierende Zeiger ausgedrückt. Dabei verändern sich sin(ω·t) und cos(ω·t) und die jeweiligen Komponenten in Richtung der vertikalen Achse. Die von außen angelegte Spannung U(t) ist nach der Spannungsbilanz (Gl. *) die vektorielle Summe der Teilspannungen. |
VIII Stromkreis mit Widerstand und Kondensator:
Hochpass und Tiefpass
Der Widerstand sei R, die Kapazität des Kondensators C. Die Schaltung wird auch RC-Glied genannt.
|
|
Abb. 4: |
Berechnung der Teilspannungen im RC-Glied
Bisher haben wir die Reaktion einer Schaltung auf eine sinusförmige Spannung bestimmter Kreisfrequenz ω untersucht. Im Folgenden geht es aber um ein Frequenzgemisch von sinusförmigen Spannungen beliebiger Kreisfrequenzen.
Ausgangspunkt ist der Zusammenhang zwischen der Stromstärke I (durch alle Bauteile) und der Spannungsabfall am Ohm'schen Widerstand UR:
UR = I·R bzw. für die Maximalwerte: UR0 = I0·R. Um den Maximalwert von UC zu ermitteln, erweist sich der Wechselstrom-Widerstand des Kondensators ZC als nützlich: UC0 = I0·ZC = I0·/(ω·C).
I0 finden wir mittels der von außen angelegten Spannung U0 = √(UR02 + UC02) = I0·√[R2 + 1/(ω·C)2] (aus der vektoriellen Summe von UR und UC). U0 ist der Scheitelwert von U(t).
Ein erstes Ergebnis ist der Gesamt-Wechselstrom-Widerstand der Reihen-Schaltung von R und C:
ZRC = U0/I0 = √[R2 + 1/(ω·C)2] = R √[1 + 1/(ω·R·C)2]
Der Wechselstrom-Widerstand ZRC wächst mit zunehmender Kreisfrequenz ω.
Uns interessieren mehr UR0 und UC0, also UR0 = I0·R = U0 · R/ZRC und UC0 = I0·ZC = U0 · ZC/ZRC.
Greifen wir die Spannung UR am Ohm'schen Widerstand ab, dann erhalten wir ihren Maximalwert: UR0 = U0 · 1/√[1 + 1/(ω·R·C)2].
Wenn ω => 0 strebt, wächst UR0 immer mehr mit dem Grenzwert UR0 = U0: Wenn U(t) aus einem Frequenzgemisch zusammengesetzt ist, dann erscheinen am Ohm'schen Widerstand vor allem die tiefen Frequenzen. Das RC-Glied mit Abgriff am Ohm'schen Widerstand wirkt als Tiefpass, weil es vor allem die Anteile mit den tiefen Frequenzen passieren lässt.
Wenn ω => ∞ strebt, wächst UC0 immer mehr mit dem Grenzwert UC0 = U0: Wenn U(t) aus einem Frequenzgemisch zusammengesetzt ist, dann erscheinen am Kondensator vor allem die hohen Frequenzen. Das RC-Glied mit Abgriff am Kondensator wirkt als Hochpass, weil es vor allem die Anteile mit den hohen Frequenzen passieren lässt.
Zum Beispiel beim Bau von Lautsprecher-Boxen spielen Hochpass und Tiefpass eine wichtige Rolle, weil man damit Hochton-Lautsprecher und Bass-Lautsprecher getrennt optimal versorgen kann.
IX Stromkreis mit realer Spule
|
|
Abb. 5: Zeigerdiagramm zum Wechselstromkreis mit einer realen
Spule: Der Zeitverlauf der Spannungen wird durch rotierende
Zeiger ausgedrückt.
|
Wir gehen wieder aus von I und UR: Aus UR = I·R erhalten wir die Maximalwerte: UR0 = I0·R. Um den Maximalwert von UL zu ermitteln, erweist sich der Wechselstrom-Widerstand der Spule ZL als nützlich: UL0 = I0·ZL = I0·ω·L.
I0 finden wir mittels der von außen angelegten Spannung U0
= √(UR02 + UL02) = I0·√[R2
+ (ω·L)2] = I0·R·√[1 + (ω·L/R)2]
(aus der vektoriellen Summe von UR und UL). Wir
erhalten also ZRL = U0/I0 = √[R2 +
(ω·L)2]
Wenn ω => 0 strebt ZRL => R, wenn <ω => ∞
oder R => 0 strebt ZRL => ω·L. Wie du es für die reale
Spule erwarten konntest, wird der Wechselstrom-Widerstand der realen Spule
niemals 0.
Damit: UL0 = U0·ω·L·√[R2 + (ω·L)2]
= U0·√{[R/(ω·L)]2 + 1}
Wenn ω => ∞ strebt UL0 => U0, wenn ω => 0 strebt UL0 => 0. Du hättest ja auch erwartet, dass im ersten Fall die Spule sperrt; die ganze Spannung U(t) mit dem Scheitelwert U0 liegt an der Spule. Im zweiten Fall findet keine Induktion statt, so als wäre die Spule nicht vorhanden, und die ganze Spannung fällt schon an R ab.
Ermittlung des Phasenwinkels:
Wenn UR(t) = UR0·sin(ω·t) ist U(t) = U0·sin(ω·t + φ). Aus dem Zeigerdiagramm erhältst du: tan(φ) = UL0/UR0 = I0·ZL / I0·R = ω·L/R.
X Differenzialgleichung für in Serie geschaltete Bauteile
Aus der Spannungsbilanz (Gl. *) erhalten wir durch Zeitableitung:
|
(Gl.
**) R dI/dt + I/C + L d2I/dt2
= dU/dt |
Es handelt sich um eine DGL zur Ermittlung der zeitabhängigen Stromstärke I(t). Die Zeitableitung dU/dt ist mit der angelegten äußeren Wechselspannung vorgegeben. Es gilt mit U = U(t) = U0 sin (ω·t): dU/dt = ω·U0 cos(ω·t).
Gl. ** stellt eine inhomogene lineare DGL 2. Ordnung mit konstanten Koeffizienten R, 1/C und L dar. Nach der Theorie der DGL erhält man die allgemeine Lösung als Summe einer speziellen Lösung und der allgemeinen Lösung der homogenen DGL. Im Folgenden geht es nur um die Gewinnung einer speziellen Lösung für I(t).
Sie lässt sich durch den Ansatz lösen:
(1) I = A sin(ω·t) + B cos(ω·t) mit den 2 noch unbekannten Konstanten A und B, oder auch mit
(1') I = I0 sin[(ω·t + φ)] mit den 2 noch unbekannten Konstanten I0 und φ, oder auch mit
(1") I = I0 exp[i(ω·t + φ)]
Wir lösen die DGL erst für den Fall mit R = 0 (bei idealer Spule und
idealem Kondensator) mit dem Ansatz (1). Dann gilt:
d2I/dt2 = - ω2I , und wir erhalten
dU/dt = I(1/C - L ω2) .
Wenn U = U0 sin (ω·t), also dU/dt = ω·U0 cos(ω·t), folgt, da (Gl. **) für alle Zeiten gültig ist, A = 0, und ω·U0 = B (1/C - Lω2), also I0 = B. Der Wechselstrom-Widerstand Z wird damit
Z = U0/I0 = (1/C - Lω2)/ω = 1/(ωC) - Lω = L/ω·(ω02 - ω2). (Es gilt auch: Z = ZC - ZL )
Z verschwindet, wenn ω = ω0 , wobei ω0 = 1/√(LC), wenn also ZC = ZL. Die Stromstärke wächst dann theoretisch über alle Grenzen. Dann haben beide Spannungen UC und UL gleichen Betrag. Das Minuszeichen weist auf die Gegenphasigkeit hin: UC und UL sind entgegengesetzt gleich. Man spricht von Resonanz mit der Resonanzfrequenz ω0 = 1/√(LC). Für alle Frequenzen sind Spannung und Stromstärke um 900 phasenverschoben gegeneinander: Wenn U = U0 sin(ω·t) folgt I(t) = U0/Z · cos(ω·t). Wenn ω0 > ω ist der Faktor Z > 0, wenn ω0 < ω ist der Faktor Z < 0. Im ersten Fall eilt die Spannung U der Stromstärke voraus, im zweiten Fall ist es umgekehrt.
Auch bei realen Bauteilen heißt eine Reihenschaltung von Spule und Kondensator manchmal "Saugkreis", weil sie im Resonanzfall einen sehr großen Strom durch den Stromkreis "saugt". Für ω => 0 oder ω => ∞ wächst der Wechselstrom-Widerstand über alle Grenzen: die Serienschaltung von L und C "sperrt".
Mit dem Ansatz (1') gilt ebenfalls:
d2I/dt2 = - ω2I , und wir erhalten
dU/dt = I/C + L d2I/dt2 = I(1/C - L ω2) oder I = dU/dt / (1/C - Lω2) = dU/dt / ω(1/ωC - Lω)
und mit I = I0 sin[(ω·t + φ)] und U = U0 sin (ω·t) [also dU/dt = ω·U0 cos(ω·t)]
I0 = ω·U0 /(1/C - Lω2) = U0 / (1/ωC - Lω) und φ = 900. Der Wechselstrom-Widerstand ist also Z = U0 /I0 = 1/ωC - Lω = ZC - ZL .
Wenn C => ∞ oder L = 0 erhalten wir das Ergebnis für Fall II oder Fall III, und für die Resonanz Z = 0.
Im allgemeinen Fall (R > 0) wählen wir lieber den Ansatz (1'). Wegen dI/dt = iω·I und d2I/dt2 = - ω2I erhalten wir dann:
dU/dt = - iR·ω·I + I/C - L ω2I = I (- iR·ω + 1/C - L·ω2) = I·ω [- iR + L·(ω02/ω - ω)] = I [- iR·ω + L·(ω02 - ω2)] bzw.
| dU/dt | = | I |·ω √[R2 + L2((ω02/ω - ω))2] und
|
| I | = I0 = ω·U0 1/√[(R·ω)2 + L2 ·( ω0 2 - ω2)2] = U0 / √[R2 + L2( ( ω0 2 / ω - ω ))2] |
|
Z = U0 / I0 = 2 + L · ( ω0 2 / ω - ω ) 2 ] = √[R2 + (1/ωC - Lω)2] = √[R2 + (Lω)2·(ω02/ω2 - 1)2] |
Z wird minimal, wenn ω0/ω = 1, nämlich Z = R . Für ω => ∞ und ω => 0 divergiert Z. Anschaulich: Für kleine Frequenzen sperrt der Kondensator, für große die Spule. Dazwischen gibt es eine Kreisfrequenz ω, bei der C und L "sich gemeinsam auf einen endlichen Strom geeinigt haben", nämlich, wenn ω der Resonanzfrequenz ω0 entspricht. Im Resonanzfall gilt ZL = ZC = 1/ (ω0C) = ω0L = 1/(C/√LC) = √(L/C). Dann ist Z = R. Die Spannungsamplitude am Kondensator oder der Spule ist UC0 = I0 ·ZC = U0/R · √(L/C) = U0/2π ·T/τ. Insbesondere, wenn die Schwingungsdauer T = 2π/ω sehr viel größer als die "Dämpfungszeit" τ = RC, ist, kann die Schwingungsamplitude an Kondensator und Spule sehr viel größer als die Amplitude der angelegten Spannung sein. Z.B. bei Flachbildschirmen wird das zur Hochspannungserzeugung für die Hintergrundbeleuchtung verwendet, ähnlich auch bei den quecksilberhaltigen Energiesparlampen.
Hochpass/Tiefpass:
L = 0 => Z = √[R2 + (1/ωC)2] => I0 = U0 /Z
UC0 = ZC·I0 = U0 · ZC/Z = 1/{ ωC · √[R2 + (1/ωC)2]} = 1/{ √[(ω·R·C)2 + 1]}
UR0 = R ·I0 = U0 · R/Z = 1/{ 1/R · √[R2 + (1/ωC)2]} = 1/{ √[1 + 1/(ω·R·C)2]}
Wenn ω => 0 strebt UC0 => U0 und UR0 => 0. Wenn ω => ∞ strebt UC0 => 0 und UR0 => U0 . Wenn man bei einem Frequenzgemisch aus vielen ω's die Spannung UC0 misst, erhält man vor allem die niederen Frequenzanteile (Tiefpass). Misst man dagegen UR0, misst man vor allem die hohen Frequenzanteile (Hochpass).
|
|
Abb. 6: Zeigerdiagramm für eine Serienschaltung von R, C
und L für eine Berechnung ohne DGL |
Schülerversuchsbaustein: "stromkompensierte Drossel" (L = 0,1 H bis 0,8 H, wobei R = 1,5 Ohm bis 6 Ohm)
( Februar 2021 )