Wenn zwischen zwei Messgrößen, z.B. y und x,  ein linearer Zusammenhang besteht, kannst du das in einem x-y-Diagramm mit einem Blick feststellen:

(y nach oben, x nach rechts; andere nennen das ein y(x)-Diagramm)

Es ergibt sich eine Gerade, bei einer direkten Proportionalität sogar eine Ursprungsgerade.

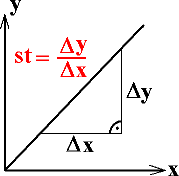Abb. 1: Steigung st im x-y-Diagramm bei einer linearen Funktion und Steigungsdreieck zur Berechnung der Steigung Δy/Δx .

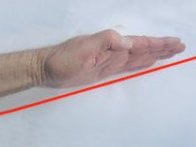
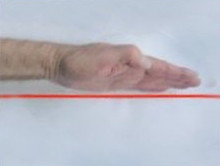
Eine Eigenheit einer Geraden ist ihre konstante Steigung Δy/Δx . Eine Steigung wird bei linearen Funktionen mit einem Steigungsdreieck berechnet (Abb. 1). Mit Hilfe deiner Hand kannst du sogar ein Gefühl für das Verhalten einer Steigung gewinnen (Abb. 2). Die Hand zeigt dabei immer von links nach rechts. Du kannst so leicht das Vorzeichen der Steigung erkennen und ob eine Steigung größer oder kleiner als eine andere ist.

				Abb. 2: "Manuelle" Vorstellung einer Steigung
a) "große" positive Steigung	b) "kleine" positive Steigung	c) Steigung 0	d) negative Steigung

Bei einer Ursprungsgeraden kann man einen Eckpunkt des Steigungsdreiecks in den Ursprung legen. Dann kann man statt Δy/Δx auch y/x schreiben.

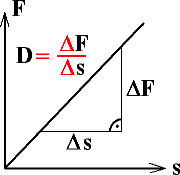
Für einige Gesetze mit direkten Proportionalitäten hat die Steigung sogar physikalische Bedeutung (Abb. 3).

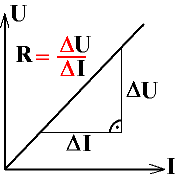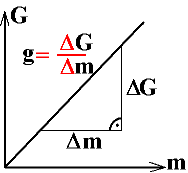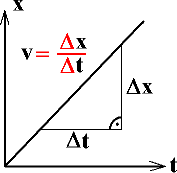Abb. 3: Hier hat die Steigung physikalische Bedeutung: Widerstand R, Federhärte D, Ortsfaktor g, Geschwindigkeit v bei einer gleichförmigen Bewegung

.

Wenn keine lineare Funktion vorliegt, kann in dieser Weise eine Steigung nur näherungsweise in kleinen Abschnitten definiert werden, in denen sich die Funktion "näherungsweise linear" verhält. Indem man die Dimensionen des Steigungsdreiecks gegen 0 streben lässt, kommt man zu einer exakten Definition einer Steigung, den "Differenzialquotienten" oder die "Ableitung".

.

( Juni 2014 )