Vgl. bzgl. weiterer
Informationen:
|
|
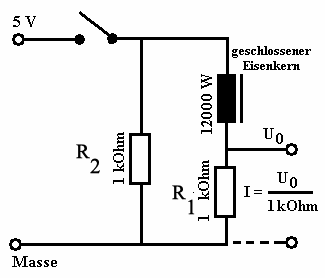
Abb. 1: "Grundschaltung" zur
Untersuchung von Ein-/Ausschaltvorgängen an der Spule
Die Stromstärke I wird hier durch die Spannung U0 am
Widerstand R gemessen, z.B. mit einem Messinterface. An der
Schaltung liege die Spannung UB (hier = 5 V).
Der vom Spulenstrom durchflossene Gesamtwiderstand
Rges enthält auch den Innenwiderstand der Spule. Rges
nennen wir auch R (Einschaltvorgang: R = Ri
+ R1).
Nach Unterbrechung des Schalters (Ausschaltvorgang)
fließt der Spulenstrom auch durch den Widerstand R2.
Der durchflossene Gesamtwiderstand ist dann R' = R + R2.
|
Schließt man in der Schaltung nach
Abb. 1 den Schalter, so steigt die Stromstärke erst allmählich an.
Umgekehrt, öffnet man den Schalter nach langer Zeit wieder, so klingt
der Strom erst allmählich ab. Die Stromrichtungen erkennst du in
den folgenden Abbildungen.
|
|
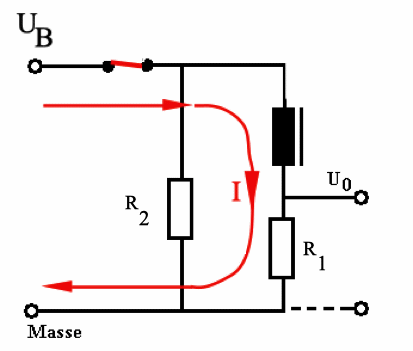
Abb. 2:
Vor dem Einschalten sei die Spule stromlos.
Nach dem Einschalten
versucht sie diesen Zustand beizubehalten, indem sie eine
Spannung induziert, die nach der Lenz'schen
Regel der angelegten Spannung
(hier 5 V) entgegenwirkt. Nach längerer Zeit fließt ein
konstanter Strom durch die Spule ("Sättigungsstrom").
(Durch R2
fließt jetzt auch ein Strom, der aber mit dem Spulenstrom nichts
zu tun hat und deshalb hier nicht betrachtet wird).
Der Gesamtwiderstand, durch den der Spulenstrom fließt, ist
zusammen mit dem Innenwiderstand der Spule (Ri):
R = Ri +
R1.
|
|
|
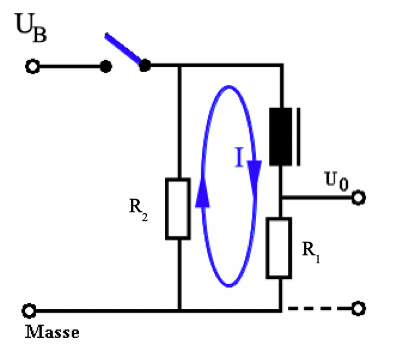
Abb. 3:
Nach Öffnen des Schalters versucht die
Spule, auch diesen neuen Zustand (Strom durch Spule)
beizubehalten, indem sie gemäß der
Lenz'schen Regel
eine Spannung induziert, die den Sättigungsstrom
kurzzeitig weiter fließen lässt. Die Spannungsquelle ist
abgetrennt, also fließt dieser Strom durch den geschlossenen
Stromkreis über R2.
Er ist jetzt ein Induktionsstrom.
Der Gesamtwiderstand, durch den der Spulenstrom
fließt, ist jetzt mit dem Innenwiderstand der Spule (Ri):
R' = Ri
+ R1 + R2.
Da jetzt der Gesamtwiderstand um
R2
vergrößert ist, muss die Induktionsspannung von größerem Betrag
als UB
sein.
(Dass die Spule vorher magnetische Energie gespeichert hatte,
ermöglicht es ihr, einen Strom zu erzeugen.)
|
Dominierende Gesetze
Die Vorgänge bei der Spule werden in der Schule durch drei
didaktisch wichtige Bedingungen dominiert. Die vierte Bedingung ist eine
Folgerung:
|
Spule
|
|
"Grundgesetz der Spule" (1)
|
(1) Uind = - L·dI/dt
(Induktionsgesetz) bzw. Spannungsabfall an der Spule UL
= - Uind.
|
|
Spannungsbilanz (2)
|
Seit dem Zuschalten einer Batterie mit
Spannung UB (alle übrigen Spannungen werden als
Spannungsabfälle aufgefasst):
(2a) UB
= I · R + UL
mit UL > 0 , da Uind =
- UL der Batteriespannung entgegengesetzt gerichtet
ist.
Gleichwertig ist die Maschenregel, wenn
auch Uind als Spannungsquelle aufgefasst wird:
(2b) UB
+ Uind =
I · R.
Anfangs fließt kein Strom (I = 0), also Uind(t=0) =
- UB .
Seit dem Abtrennen der Batterie:
(2c) 0 = I · R' + UL
mit UL < 0, damit I weiterhin positiv. Für
alle Zeiten gilt Uind = I · R'.
R und R' sind die jeweils vom Strom I
durchflossenen Gesamtwiderstände.
R' = R + R2
, weil der Spulenstrom nach dem Abtrennen auch durch R2
fließt!
(Es ist egal, ob du mit
Gleichung (2a) oder (2b) argumentierst. Beachte aber, dass Uind
= - UL auf unterschiedlichen Seiten der Gleichung
stehen.)
|
|
Stetigkeitsbedingung für die
Stromstärke (3)
|
Die Stromstärke macht keine Sprünge.
|
|
Stationärer Strom
("Sättigungsstrom") (4)
|
Das ist die Sättigungs-Stromstärke I, die sich
einstellt, wenn keine Induktion mehr stattfindet, also, wenn UL
= 0 => I aus UB = I · R lange nach dem
Einschalten , bzw. I = 0 lange nach dem Abtrennen
der Batterie.
|
Die Stetigkeitsbedingung hängt
mit
der Anfangsbedingung I(t=0) beim Einschalten zusammen. Sie bestimmt auch
die Spitzenspannung,
wenn noch I = 0 (Einschaltvorgang), bzw. wenn der stationäre Strom nach
dem Abschalten der Batterie weiterfließen muss:
|
Es muss eine solche Spannung induziert werden,
dass I kurzzeitig unverändert bleibt.
|
(Die Gleichung (2a): UB = I · Rges
- L·dI/dt , oder (2b und 2c) ist eine Differenzialgleichung
(DGL) 1. Ordnung
für den Spulenstrom I. Sie heißt so, weil neben I die
Zeitableitung von I (dI/dt) vorkommt. Sie benötigt nur eine
Anfangsbedingung, hier den Strom im Moment des Einschaltens bzw. des
Ausschaltens.)
dI/dt im Induktionsgesetz kann je nach Situation oder
Kenntnisstand aufgefasst werden als Zeitableitung der Stromstärke oder
als Differenzenquotient ΔI/Δt .
Beispiele für einfache Rechnungen
Es gelten die Daten von Abb. 1. Für den Einschaltvorgang
folgt der stationäre Strom folgendermaßen: Nach langer Zeit: UL
= 0, also auch Uind = 0, also mit der Spannungsbilanz (2): UB
= I · R . Daraus folgt bei einem Innenwiderstand der Spule von 2 kΩ und
R1 = 1 kΩ der stationäre Strom ("Sättigungsstrom")
I = UB/R = 5,0 V / 3,0 kΩ = 1,7 mA.
Nach dem Öffnen des Schalters muss dieser Strom
weiterfließen, also entsteht eine Spitzenspannung Uind = - UL
= I · R' = 1,7 mA · 4,0 kΩ = 6,7 V. Sie hat gleiches Vorzeichen wie UB,
weil sie einen gleichgerichteten Strom durch die Spule fließen lassen
muss. Sie muss größer als UB sein, weil der unveränderte
Strom durch R1, den Innenwiderstand der Spule Ri und
R2 gepumpt werden muss.
Unmittelbar nach dem Schließen des Schalters ist die
Stromstärke noch 0, also nach der Spannungsbilanz (2): UL = UB
bzw. die Spitzenspannung Uind = - UB = - 5,0 V.
Sie hat umgekehrtes Vorzeichen im Vergleich zu UB , weil sie
den Stromfluss zu unterdrücken versucht, zunächst sogar vollständig.
Wie kann man die Spannung an der Spule (Uind
= - UL) messen? Dazu
findest du mehr hier.
Im Schülerversuch mit Messinterface und
PC entstanden folgende Bilder (oben Uind, unten
I):
|

|

|
|
Abb. 4: Leider sind hier die Widerstände
R1 und R2 schwer erkennbar. Die
Leitungen rechts führen zum Messinterface.
Aus UB und dem Gesamtwiderstand R,
der beim Einschaltvorgang den Widerstand R1 und
den Innenwiderstand der Spule Ri enthält, wird Uind
berechnet. Das geschieht z.B. im Messinterface.
|
Abb. 5: Spannung UL (auf dem Bildschirm
oben) und Stromstärke I bei einer Spule.
Du kannst dir leicht überlegen, wie sich die Vorzeichenumkehr
auf die Induktionsspannung Uind = - UL
auswirkt. Dann erkennst du, dass beim Einschalten eine Gegenspannung
zur Batteriespannung herrschen sollte, und beim Ausschalten
eine Mitspannung, die anfänglich denselben Strom wie
die Batterie durch die Spule pumpen sollte.
Durch Abgriff direkt an der Spule könnte man mit dem
Messinterface in der Schaltung links die Spannung UL
nur dann erhalten, wenn ihr Innenwiderstand vernachlässigbar
wäre.
|
|
(Achte darauf, dass die
Selbstinduktionsspannung beim Ausschalten die zulässige
Eingangsspannung des Messinterfaces nicht
überschreitet! Beachte die unterschiedlichen
Vorzeichen der Selbstinduktionsspannung! Sie erfordern evtl.
bipolare Messung im Messinterface! )
|
Eine kurze Geschichte des Ein- und
Ausschaltvorgangs bei der Schaltung der Abb. 1
Spulen sind nach der Lenz'schen
Regel extrem konservativ, d.h. sie
versuchen, alles beim Alten zu belassen. Wenn kein Strom fließt,
"wollen" sie den Strom weiterhin auf 0 halten, wenn ein Strom fließt,
"wollen" sie diesen weiterhin in möglichst unveränderter Stärke weiter
fließen lassen. Eine andere Aussage dieser Tatsache ist, dass die
Stromstärke keine Sprünge macht.
Einschaltvorgang: Solange in Abb. 1 der Schalter
offen ist, ist die Stromstärke 0. Nach Schließen des Schalters
induziert die stromdurchflossene Spule eine Gegenspannung,
die den Strom I weiterhin kurzzeitig auf 0 hält. Allmählich steigt die
Stromstärke doch an. Im geschlossenen Stromkreis liegen zwei
Spannungsquellen für die Batteriespannung und die Induktionsspannung,
welche als Gegenspannung wirkt. Anfänglich heben sie sich gegenseitig
auf, ihre Summe verschwindet, also Uind = - UB.
Im Allgemeinen erzeugen sie zusammen den Spannungsabfall I·R am
stromdurchflossenen Gesamtwiderstand R. Mit zunehmendem Strom wird der
Betrag der Induktionsspannung kleiner, sie kann also immer weniger den
Stromanstieg verhindern. Im Prinzip nach sehr langer Zeit t1
erreicht die Stromstärke schließlich ihren Maximalwert I1 =
UB/R, den Sättigungsstrom, wenn die Induktionsspannung 0
geworden ist. Dann gilt UB = I1·R, und die in
der Spule gespeicherte Energie ist maximal.
Ausschaltvorgang: Nach Öffnen des Schalters
sorgt die Spule mit einer Selbstinduktionsspannung dafür, dass der
Strom I1 = UB/R (Sättigungsstrom) kurzzeitig
weiterfließt. Wenn der Widerstand R2 in Abb. 1 vorhanden
ist, muss dieser Strom durch den Innenwiderstand der Spule, den
Widerstand R1 und auch R2 fließen. Weil der
Gesamtwiderstand jetzt R' = Ri + R1 + R2
ist, wird dazu eine Induktionsspannung benötigt, deren Betrag die
Batteriespannung UB überschreitet. Es gilt Uind =
I1·R' = UB · R'/R > UB. Da sie
anfänglich den unveränderten Strom I1 mit unveränderter
Richtung fließen lässt, muss sie gleiches Vorzeichen wie UB
haben, sie ist eine "Weiter- oder Mitspannung". Ist
kein Widerstand R2 vorhanden (ist R' also quasi beliebig
groß), müsste eine beliebig große Spannung induziert werden. Schon
zuvor wird z.B. die Luft zwischen den Kontakten des Schalters
leitfähig, und der Schalter wird so quasi wieder geschlossen, häufig
erkennbar an einem Öffnungsfunken. Dazu ist evtl. eine riesige
Induktionsspannung nötig, die Bauteile der Schaltung zerstören
könnte. Schon weil nur endlich viel magnetische Energie in der Spule
gespeichert ist, muss die Stromstärke I allmählich absinken. Mit
absinkender Stromstärke wird auch die Induktionsspannung kleiner,
und sie verhindert das Absinken noch weniger. Nach sehr langer Zeit
sind Stromstärke und Induktionsspannung auf 0 abgesunken.
Gesetzmäßigkeiten
Errate eine Lösung der Differenzialgleichung (DGL)
(2a) bzw. (2c) mit einem geeigneten Ansatz
Von der Lösung der DGL sind folgende Grundfakten
für Stromstärke und Induktionsspannung bekannt (der Pfeil =>
bedeutet: strebt gegen):
Einschaltvorgang:
1. t = 0: I(t=0) = 0, und Uind(t=0)
= - UB
2. t = t1:
I(
t1) = I1 und
für sehr großes t1:
I(
t1) = UB/R
und Uind(t=>t1)
=> 0
Ausschaltvorgang:
1. t = t1: I(t1)
= I1 = UB/R
und Uind(t=t1) = UB ·
R'/R = I1·R' (für sehr großes t1),
2. t => ∞: I(t
=> ∞) => 0 und
Uind(t=> ∞)
=> 0
Für den Einschaltvorgang
liegt also z.B. der Ansatz
nahe:
I(t) = UB/R·
[1 - exp(-t/T)] und mit dem Induktionsgesetz,
wenn T = L/R:
Uind = - UB·
exp(-t/T) mit irgendeiner Konstanten T.
Überprüfe die Grundfakten:
1. für t = 0:
I(t=0) = 0
und Uind =
-
UB .
Wegen des Minuszeichens ist Uind
eine Gegenspannung zur
Batteriespannung.
2. für t => ∞:
I(t) => UB/R
und Uind =>
0.
Die Grundfakten für den Einschaltvorgang werden
richtig beschrieben. Die Richtigkeit des Ansatzes kann auch bewiesen
werden. Das soll hier aber nicht ausgeführt werden.
Ähnlich machen wir für den Ausschaltvorgang
(t ≧ t1)
den Ansatz:
(Der Ausschaltvorgang beginnt zur Zeit t = t1.
Alle weiteren Zeiten sind auf diesen Zeitpunkt bezogen; deswegen
die Differenz t-t1.
Der Startwert bei t = t1
ist wegen der Stetigkeitsbedingung I(t=t1)
= UB /R
(für sehr großes t1). Für t
>> t1
strebt I(t) => 0. )
I(t) = UB/R
· exp[-(t-t1)/T']
daraus folgt für t ≧ t1,
wenn T' = L/R':
Uind
= UB ·
R'/R · exp[-(t-t1)/T']
und es gilt: Uind
= I · R'
Überprüfe die Grundfakten:
1. für t = t1:
I(t)
= UB/R
und
Uind =
+ UB ·
R'/R , wenn T' = L/R'
Wegen des positiven Vorzeichens ist Uind
eine "Mitspannung", deren Spitzenwert wegen R'
> R die Betriebsspannung übersteigt.
2. für t => ∞:
I(t) => 0 und Uind
=> 0.
Die Grundfakten für den Ausschaltvorgang
werden durch den Ansatz richtig beschrieben. Der Ansatz kann
wieder bewiesen werden, was
wiederum hier nicht ausgeführt werden soll.
Wegen Uind = I· R' sind Uind und I
zueinander proportional, haben also die gleiche Zeitabhängigkeit. Das
sieht nach dem Ohm'schen Gesetz aus. Außer der Spule als Spannungsquelle
mit Uind enthält der Stromkreis auch nur einen Ohm'schen
Widerstand.
Eine Lösung der DGL mit einem
Standardverfahren findest du hier.
Was ist die charakteristische Zeit T =
L/R bzw. T' = L/R'?
Beim Einschaltvorgang gilt dI/dt = UB/L -
I·R/L, also dI/dt = UB/L, wenn I = 0 bzw. für t = 0:
dI(t=0)/dt = UB/R · R/L = UB/R
· 1/T. Das ist die Anfangssteigung der t-I-Funktion. Für die
Tangente im Nullpunkt gilt also
I = UB/R
· t/T.
Die Tangente erreicht den Sättigungsstrom UB/R
bei t = T. Damit haben wir die Deutung von T:
|
T ist diejenige Zeit, nach der die Stromstärke
den Sättigungsstrom UB/R erreichen
würde, wenn sie sich längs der Tangenten (im Ursprung)
verändern würde.
|
T = L/R wird "charakteristische Zeit für den
Einschaltvorgang" genannt, weil sie ein Maß dafür ist, wie
schnell die Stromstärke ansteigt. Sie hängt von der Induktivität L
und dem Gesamtwiderstand R des Zweigs ab, in dem der Spulenstrom
fließt. Sie kann dazu dienen, für ein Experiment eine günstige
Kombination von L und R auszuwählen, aber auch zur Messung von L.
Ganz entsprechend gilt beim Ausschaltvorgang dI(t)/dt
= - I(t)/T' , und bei t = t1: dI(t)/dt = - UB/R
· 1/T'.
|
T' ist - ausgehend vom Sättigungsstrom UB/R -
diejenige Zeit, nach der die Stromstärke den Strom 0 erreichen
würde, wenn sie sich längs der Tangenten zum Zeitpunkt des
Schalteröffnens verändern würde.
|
T' = L/R' wird "charakteristische Zeit für den
Ausschaltvorgang" genannt, weil sie ein Maß dafür ist, wie
schnell die Stromstärke abfällt. Sie hängt von der Induktivität L
und dem Gesamtwiderstand R' des
Zweigs ab, in dem der Spulenstrom fließt. T' = L/R'
< T = L/R, weil R' = R + R' > R. Der Strom
fällt beim Ausschalten schneller ab, als er beim Einschalten
ansteigt.
Dass T' mit zunehmender Induktivität L wächst, passt zur Überlegung,
dass bei größerem L mehr magnetische Energie in der Spule
gespeichert ist. T' fällt mit zunehmendem Gesamtwiderstand. Das
passt gut dazu, dass mit zunehmendem Gesamtwiderstand R' die
magnetische Energie schneller "aufgebraucht" wird.
Aus dem t-I-Diagramm lassen sich so T und T' graphisch leicht
entnehmen (Abb. 6) mit dem Ergebnis T = 0,002 s und T' = 0,001 s).
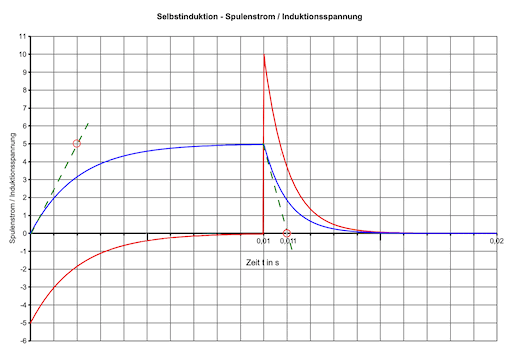
Abb. 6: Ergebnis einer
Tabellenkalkulation für L = 0,2 H, R = 100 Ω, R' = 200
Ω, UB = 5 V. Blau gezeichnet ist der Spannungsabfall
I·R. Er ist ein Maß für den Spulenstrom I.
Die Tangenten mit der Anfangssteigung bei t = 0 s und bei t = t1
sind grün eingezeichnet. Damit kannst du T bzw. T' ablesen. Wegen
T = L/R
erhältst du L = T·R = 0,002 s·100 Ω = 0,2 H oder auch
L = T'·R' = 0,001 s·200 Ω = 0,2 H.
Für die Schülerversuchsspule
mit L = 0,1 H (Ri = 1,5 Ω;
vernachlässigbar) und mit R1
= R2 = 100
Ω erhältst du in guter Näherung T = L/R = 1 ms bzw. T' = 0,5 ms.
Das Messinterface muss also schnelle Messungen zulassen.
Messtechnisch günstiger sind R1
= R2 = 10 Ω
mit T = L/R = 10 ms bzw. T' = 5 ms. Auch bei der empfohlenen
Batteriespannung UB =
1,5 V wird die Batterie beim Einschaltvorgang sehr stark belastet.
Warnung: Es gibt im
Internet so genannte "Erklärvideos" von Firmen, deren Autoren die
Vorgänge bei der Selbstinduktion nicht verstanden haben. Lass'
dich von ihnen nicht in die Irre führen. So kannst du kein
Einserschüler werden! Man hat den Eindruck, dass es solchen Firmen
mehr darum geht, Werbung unterzubringen.
Gleichwertig wäre z.B. der
Ansatz: I(t) = UB/R · [1 - 10-t/T] mit Uind
= - UB · 10-t/T, wenn T = L/[R·1/ln(10)],
da
101/ln(10)=
e .
Möglicherweise habe ich die Tangentenmethode zur
Definition von T vor Jahrzehnten durch Prof. Heuer kennengelernt.
( Juni 2014; Ergänzungen Dez. 2020; weitere
Ergänzungen April 2021)





