| C = I / ΔU/Δt |
und es gilt analog zu (*):
| I = C·ΔU/Δt (**) |
Wenn du schon den mathematischen Begriff der Ableitung kennst, könntest du (**) direkt durch Ableiten aus (*) herleiten.
|
SG037 Definition der Kapazität ©
H. Hübel Würzburg 2013
|
Versuch dazu: |
Impres-sum |
Stell' dir folgenden Versuch vor: Du lädst einen Kondensator mit unterschiedlichen Spannungen U auf. Anschließend entlädst du den Kondensator über einen Ladungsmesser und misst die vorher gespeicherte Ladungsmenge Q. Du wirst eine Proportionalität zwischen Q und U feststellen. Der Proportionalitätskonstanten
| C = Q/U |
gibt man den Namen "Kapazität". Es gilt also
| Q = C·U (*) |
Der Name Kapazität ist ganz vernünftig. Er weist nämlich
darauf hin, welche Ladungsmenge Q ein Kondensator speichern kann,
allerdings bei einer bestimmten Spannung U. Kapazität heißt ja
soviel wie Fassungsvermögen. Das darf dich aber nicht zur Annahme
verführen, dass ein Kondensator nur ein begrenztes Fassungsvermögen für
Ladungen hätte. Denn, wenn du die Spannung erhöhst, kannst du noch mehr
Ladungen speichern. (Das geht gut, solange der Kondensator nicht
"durchschlägt", d.h. solange der Isolationswiderstand zwischen beiden
Kondensatorplatten ausreicht.)
Gemäß der Definition C = Q/U hat die Kapazität die Einheit [C] = 1 As/V = 1 F. Ein Kondensator hätte also die (unrealistisch große) Kapazität von 1 F, wenn er bei einer Ladespannung von 1 V die Ladungsmenge 1 C = 1 As aufnehmen könnte.
Zu Ehren von Michael Faraday wurde zur Abkürzung 1 F ("Farad") eingeführt. In der Elektronik werden Kapazitäten von 1 pF (Picofarad) über 1 nF (Nanofarad) bis einige µF (Mikrofarad) verwendet. Sie können typischerweise bis zu einer maximalen Spannung von 5 V, oder bei anderen Ausführungen, bis zu wenigen 100 V betrieben werden.
Dynamische Definition:
  |
Man könnte C auch dynamisch einführen und messen:
Mit Hilfe einer so genannten "Strompumpe"
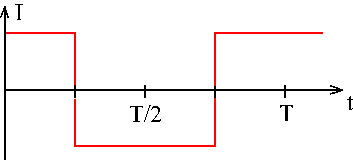
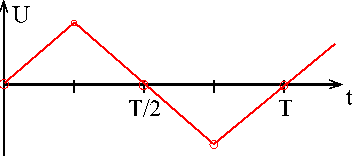
(Erläuterung für den Lehrer) schickt man einen konstanten Strom
oder abschnittsweise konstanten Strom durch den Kondensator.
Dann verändert sich die Kondensatorspannung linear; das
t-U-Diagramm hat in jedem Zeitabschnitt Δt eine konstante Steigung
ΔU/Δt, die proportional ist zur Stromstärke I. Dann wird als
Proportionalitätskonstante definiert:
und es gilt analog zu (*):
Wenn du schon den mathematischen Begriff der Ableitung kennst, könntest du (**) direkt durch Ableiten aus (*) herleiten. |
| C = ε0·εr · A/d |
mit der elektrischen Feldkonstanten ε0 , der relativen Dielektrizitätskonstanten εr , der Plattenfläche A und dem Plattenabstand d.
Warnung:
Ich habe ein Video zur Kapazität gefunden:

Leider werden am Schluss, wenn es um ein dielektrisches
Medium im Plattenkondensator geht, Märchen erzählt. Es wird auch nicht
geklärt, ob das Medium, wie dort im Bild dargestellt, den Kondensator
nur teilweise erfüllt oder vollständig, es wird nicht zwischen den
Feldern E und D unterschieden, und ob der Kondensator
während des Einschiebens mit der Spannungsquelle verbunden bleibt oder
nicht. So geht es nicht!