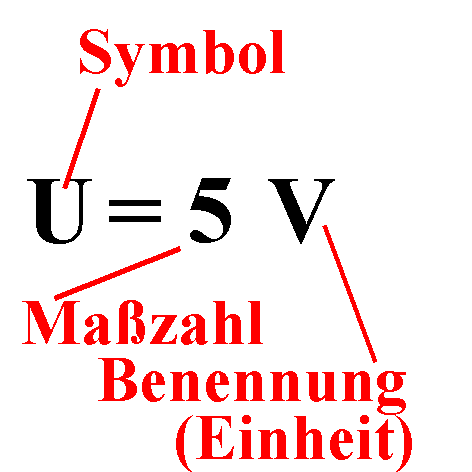
 |
Es wird jetzt ein neuer Name vereinbart: J/As soll mit V ("Volt") abgekürzt werden:
|
|
SG024 Spannung U zwischen zwei Punkten und Ringspannung U ©
H. Hübel Würzburg 2013, 2022
|
Impres-sum |
Wenn du einen elektrischen Stromkreis mit einem abgeschlossenen *) Heizungsstromkreis vergleichst, erkennst du, dass
Im elektrischen Fall besteht diese "Substanz" aus elektrischen Ladungen, im Fall der Heizung aus dem warmen Wasser, das Wärme in die Heizkörper transportiert. Im elektrischen Fall ist die "Stromquelle" zugleich Pumpe und Energiequelle, im Heizungsfall ist die Pumpe eine mechanische Umwälzpumpe, die Energiequelle der Brenner. Der mechanischen Reibung entspricht im elektrischen Fall der Widerstand eines Bauteils. Durch ihn entsteht aus Stromarbeit "Wärme".
Beim elektrischen Stromkreis aus bestimmten widerstandslosen Materialien ("Supraleitern") gibt es aber die Situation, dass - nach einmaligem "Anstoß" - ein dauernder Strom fließt ohne eine "Pumpe".
Wie schnell die "Substanz" in beiden Fällen fließt, welche Energie pro Zeiteinheit (Leistung) aus der Energiequelle herausgepumpt wird, hängt u.a. von Eigenschaften der Pumpe ab. Es ist naheliegend, so etwas wie eine "Pumpenstärke" zu betrachten. Obwohl das kein offizieller Begriff ist, kannst du dir vorstellen, was gemeint ist, und dass sie irgendwie gemessen wird. Für den elektrischen Stromkreis ist die "Spannung der Energiequelle" ein Maß dafür.
| Vorläufig: Spannung U einer Energiequelle ist ein Maß für ihre "Pumpenstärke" . |
Je größer die Spannung/"Pumpenstärke" der Energiequelle
ist, desto größer ist (i. Allg.) für einen gegebenen Stromkreis die
Stromstärke, die die Energiequelle durch den Stromkreis pumpen kann.
Man könnte eine Einheit der Spannung z.B. dadurch definieren, dass man für eine feste Energiequelle einen Wert für die Spannung festlegt.
|
Z.B.: Die Spannung U eines geladenen Bleiakkus soll 2 V sein. |
Für viele praktische Zwecke würde das ausreichen.
Tatsächlich wird die Einheit offiziell anders, als "abgeleitete Größe",
definiert.
1. Gewöhnliche Spannung (Spannung zwischen zwei Punkten**)
Betrachte den Fall eines geladenen Kondensators (Abb. 1). Wenn eine positive "Probeladung" q von Punkt P1 zu Punkt P2 im elektrischen Feld des Kondensators verschoben wird, muss von außen eine Arbeit W > 0 verrichtet werden. Denn die positive Probeladung wird ja von der positiven Platte abgestoßen und von der negativen Platte angezogen. Die Spannung zwischen Punkt 2 und Punkt 1 wird definiert als die Arbeit pro Ladungsmenge W/q, die von außen verrichtet wird bei Verschiebung der Ladung von 1 nach 2:
|
U = W/q |
Das gilt auch, wenn die beiden Punkte auf den Kondensatorplatten liegen. Nehmen wir an, es werde eine Arbeit W von 3,2·10-19 J von außen aufgewendet, um eine positive Elementarladung q = 1,6·10-19 As von der negativen zur positiven Platte zu bewegen (ohne der Ladung kinetische Energie mitzugeben). Dann beträgt die Spannung zwischen beiden Platten
U = W/q = 3,2·10-19 J / 1,6·10-19
As = 2 J/As .
1 V =
1 J/As

Es wird jetzt ein neuer Name vereinbart:
J/As soll mit V ("Volt") abgekürzt werden:
Dann beträgt also die Spannung zwischen beiden Kondensatorplatten 2 V. Wenn das Voltmeter angeschlossen wird, wie in der Abb. 1 mit dem COM-Pol (häufig blau oder schwarz) an der negativen Platte, zeigt das Voltmeter genau +2 V an. Es gilt dann auch: 1 J = 1 V·A·s.
Statt aufgewendeter Arbeit W = q·U können wir auch sagen: übertragene Energie E. Für diese gilt dann ebenfalls E = q·U.
(Mit der Bezeichnung "übertragene" Energie
lassen wir offen, von wo bis wohin diese Energie übertragen wird.)
So haben wir also eine recht anschauliche Deutung der
Spannung U:
|
Die Spannung U zwischen zwei Punkten sagt, wie viel Energie E = q·U übertragen wird bei Verschiebung der Ladung q von einem Punkt zum anderen. |
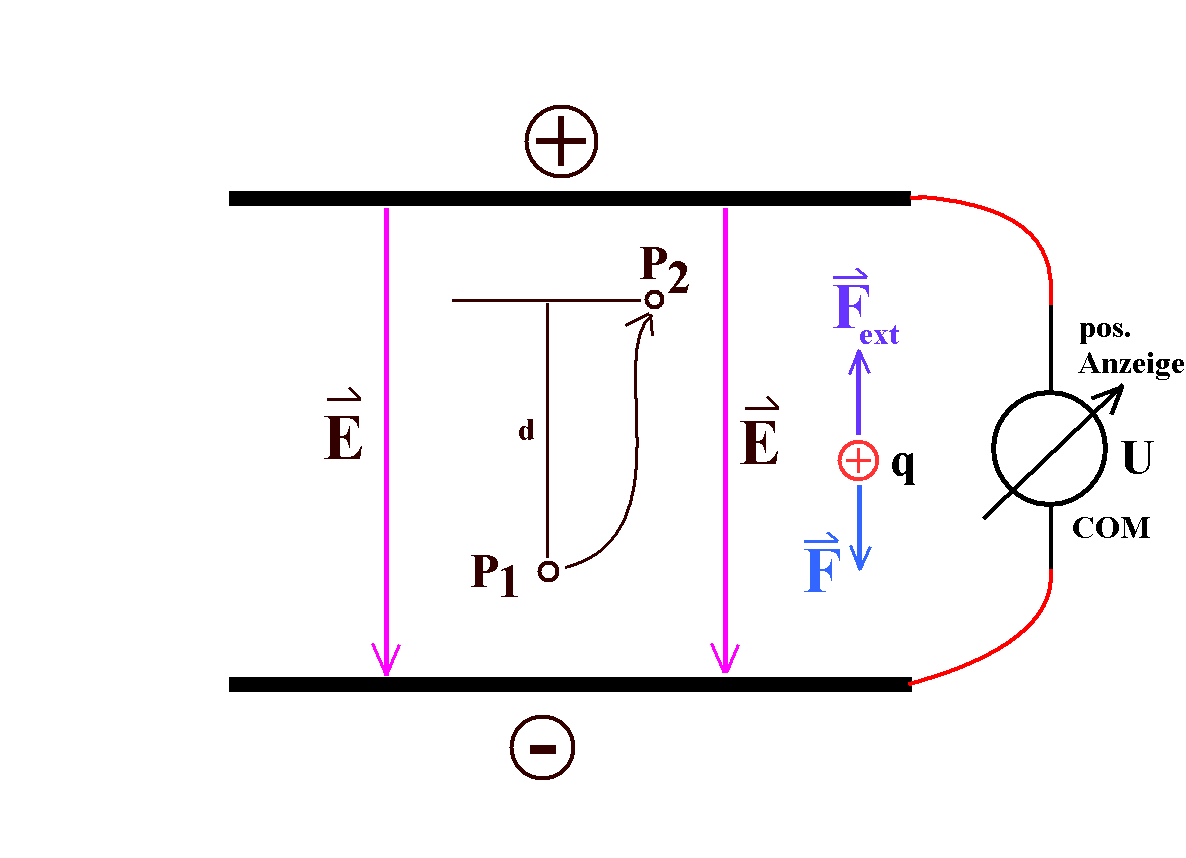 |
Abb. 1:
Es muss von außen (durch Fext) positive Arbeit verrichtet werden, wenn eine positive Probeladung von der negativen zur positiven Platte verschoben wird. U wird von einem Spannungsmesser mit richtigem Vorzeichen angezeigt, wenn sein Massepol (COM) mit dem Minuspol verbunden wird.
|
Man kann auch sagen:
|
Wenn für den Transport einer positiven Probeladung von einem Punkt zu einem anderen eine nicht verschwindende Verschiebungsarbeit aufgewendet werden muss, dann herrscht zwischen beiden Punkten eine Spannung. |
Der Transport muss dabei beliebig langsam erfolgen (es soll keine zusätzliche kinetische Energie aufgewandt werden!).
In vielen Fällen muss für jeden beliebigen Weg zwischen
beiden Punkten die gleiche Arbeit aufgewendet werden ("Wegunabhängigkeit").
Dann kann man auch jedem Punkt P eine eindeutige potenzielle
Energie W (relativ zu einem festen anderen Punkt
Q) und ein Potenzial W/q zuordnen. Das Potenzial ist dann nur
abhängig vom Punkt P. Dann liegt ein reines
(wirbelfreies) Potenzialfeld vor. Das gilt aber in anderen
Fällen nicht.
Die Verschiebungsarbeit muss gegen das elektrische Feld aufgewendet werden - es behindert diese Verschiebung. Umgekehrt, bringt man die positive Probeladung q in das elektrische Feld an den Punkt P2, so verrichtet das Feld selbst Verschiebungsarbeit, die nach außen abgegeben wird, wenn es die Ladung zum Punkt P1 zurück bewegt. Deshalb kann man in diesem Fall eine Spannung auch auffassen als Ursache für einen Strom.
Ein reines Potenzialfeld kann in einem Stromkreis mit Widerstand aber nicht die Energie für einen beständigen Strom heranschaffen. Das wird üblicherweise mathematisch bewiesen, ist aber auch anschaulich klar, da bei einem geschlossenen Weg (Rundweg) in einem Potenzialfeld die auf einem Teilweg aufzuwendende Verschiebungsarbeit auf dem zweiten Teilweg wieder gewonnen wird.
In bestimmten Fällen muss eine nicht verschwindende Verschiebungsarbeit aufgewendet werden für eine Verschiebung von einem Punkt auf einem Umweg zum gleichen Punkt zurück ("auf einem geschlossenen Weg/Umlauf"). Eine solche Situation liegt z.B. bei der (elektromagnetischen) Induktion vor. Einem bestimmten Punkt kann man hier keine Energie zuordnen. Die Energie zur Verschiebung von irgendeinem Punkt zu diesem Punkt hängt von Weg ab, auf dem das geschieht. Es ist naheliegend, hier eine Ringspannung (oder Umlaufspannung) analog zu definieren durch die Verschiebungsarbeit W für einen vollen Umlauf:
|
URing = W/q für einen geschlossenen Weg von einem Punkt zum Punkt zurück |
Es gibt offenbar keinen Unterschied in der Definition der gewöhnlichen und der Ringspannung. Es gilt immer die gleiche Definitionsformel. Sie wird nur unterschiedlich angewandt, je nachdem, ob Anfangs- und Endpunkt zusammenfallen oder nicht.
Wie die gewöhnliche Spannung hat die Ringspannung die Einheit 1 V = 1 J/C = 1 VAs/As.
Wenn diese Ringspannung von 0 verschieden ist, spricht
man häufig von einem elektrischen Wirbelfeld E. Bei der
(elektromagnetischen) Induktion entsteht immer eine von 0 verschiedene
Ringspannung. In einem reinen Potenzialfeld ist die Ringspannung wegen
der "Wegunabhängigkeit" 0. Nur dort hat eine Ladung q an einem Punkt
eine bestimmte potenzielle Energie und nur dort kann man eine
gewöhnliche Spannung zwischen zwei Punkten - irgendwie mit Worten
eingekleidet - auch als "potenzielle Energie pro Ladung" definieren.
Aber es gibt auch Energiequellen (vgl. Induktion), bei denen im
Stromkreis keine zwei Punkte identifiziert werden können, zwischen
denen eine gewöhnliche "Spannung der Energiequelle" eindeutig gemessen
werden könnte, unabhängig vom Weg zwischen den beiden Punkten. Dennoch
gibt es hier eine Induktionsspannung, die immer eine Ringspannung ist.
Hier braucht man unbedingt den Begriff der Ringspannung.
3. Messung der Ringspannung
Eine Ringspannung längs eines geschlossenen Leiterkreises mit dem Gesamtwiderstand Rring wird entweder gemessen durch den Ringstrom I, den sie hervorruft:
| Uring = I · Rring |
oder, indem der Leiterkreis unterbrochen wird, durch Überführung
in eine gleich große gewöhnliche Spannung zwischen den Enden des
Leiters.
Die Spannung U zwischen zwei Punkten ist ganz
allgemein definiert ist als Arbeit W pro Ladungsmenge für die
Verschiebung von einem Punkt zum anderen:
|
U = W/q |
Nur für ein wirbelfreies Feld wird so eine
wegunabhängige Spannung zwischen zwei Punkten definiert. W ist dabei
die Arbeit, die aufgewendet werden muss, um die Ladung q von einem
Punkt zum anderen zu verschieben. Nur bei Wegunabhängigkeit kann man
von potenzieller Energie sprechen. In anderen Fällen liefert die
Messung für unterschiedlichen Verlauf des Weges zwischen den zwei
Punkten unterschiedliche Spannungen. Das wichtigste Beispiel dazu ist
die elektromagnetische Induktion. Hier gibt es keine potenzielle
Energie.
Bei einem Wirbelfeld wird eine Ringspannung in der gleichen Weise definiert, wenn W die Arbeit zur Verschiebung der Ladung q von einem Punkt auf einem Umweg zum Punkt zurück ist. Bei der elektromagnetischen Induktion entsteht eine Ringspannung.
Spannung kann die Ursache eines Strom sein (Spannung
einer Energiequelle), aber auch die Folge eines Stroms
(Spannungsabfall an einem stromdurchflossenen Widerstand). Bei der
Selbstinduktion gibt es sogar eine Situation, bei der eine bestimmte Änderungsrate
der Stromstärke eine bestimmte Selbstinduktionsspannung zur
Folge hat.
5. Du kannst jetzt anschaulich verstehen:
Grundlage des Verständnisses ist die Kenntnis, dass Spannung
zwischen zwei Punkten definiert ist als Energieübertrag pro
Ladungsmenge bei Verschiebung der Ladung von dem einen Punkt zum
anderen, also U = E/q. (Wenn die beiden Punkte zusammenfallen, spricht
man von einer Ringspannung.)
a) An einem vom Strom I durchflossenen Bauteil liegt die Spannung U, wenn beim Transport der Ladung q = I·Δt von einem Punkt zum anderen eine Energie E = q·U übertragen wird. Dann ist die Spannung am Bauteil U = E/q (gemessen zwischen den Enden des Bauteils).
(Δt ist ein beliebiges Zeitintervall.)
b) Zwei unterschiedliche
Widerstände R1 und R2 liegen im unverzweigten
Stromkreis in Reihe geschaltet an einer Strom-/Energiequelle.
Durch sie fließt der gleiche Strom I, also n
Elektronen in der Zeit Δt.
Sie transportieren die Gesamtladung q
= e·n.
Sie fließen aus der Strom-/Energiequelle
und vermitteln insgesamt die Energieübertragung E =
U·q an den Stromkreis, wobei also U = E/(e·n)
(q = e·n). An jedem
Widerstand erleidet jedes
Elektron nacheinander verschiedene "Schicksale": Es muss sich
durch R1 und R2 "hindurch
quälen" und vermittelt so unterschiedliche Energieüberträge ΔE1
und ΔE2 an die Widerstände. Alle
Elektronen vermitteln an R1 zusammen die
Energieübertragung E1 = ΔE1·n
und an R2 die
Energieübertragung E2 = ΔE2·n,
und insgesamt mit der Energieerhaltung E = E1
+ E2. Daraus ergeben sich unterschiedliche Spannungen an
den Widerständen: U1 =
E1/q = E1/(e·n)
= ΔE1/e und U2
= E2/(e·n) = ΔE2/e.
Für die Reihenschaltung von zwei Widerständen R1 und R2
gilt also: U = U1 + U2:
| Bei einer Reihenschaltung von Widerständen addieren sich die Teilspannungen an den Widerständen zur Gesamtspannung an der Strom-/Energiequelle (= Spannung der Strom-/Energiequelle). |
Das ist ein Spezialfall einer der Kirchhoff'schen Regeln. Grund ist die Energie- und Ladungserhaltung. Teilspannung an einem Widerstand ist die Spannung zwischen Anfang und Ende des Widerstands. (Gewöhnliche) Spannungen sind immer Spannungen zwischen zwei Punkten.
Vorteil dieser Argumentation ist, dass verschiedene
Probleme nicht aufgeworfen werden, die bei Gebrauch mancher didaktischer
Modelle unnötigerweise entstehen:
1. Bei einer Driftgeschwindigkeit von 1 mm/s brauchen Elektronen nach dem klassischen Modell von einem 1 km entfernten E-Werk bis zum "Verbraucher" 1 000 000 s ≈ 277 h ≈ 11 d. So lange vorausschauend müssten sich die Elektronen ihre Energie besorgen? Wenn der offene Schalter direkt am E-Werk sitzt mit sonst lauter energielosen Elektronen im Stromkreis, dann bräuchten die energiereichen Elektronen nach Schließen des Schalters 11 – 12 Tage, bis sie an der Lampe ankommen um dort die mitgebrachte Energie abzugeben?
2. Bei Wechselstrom von 50 Hz wackeln die Elektronen nur auf einer Strecke von wenigen Atomdurchmessern hin und her. Sie befinden sich also quasi nie am E-Werk. Woher bekommen sie dann ihre Energie?
3. Woher "wissen" die Elektronen bei der
Reihenschaltung, dass sie am ersten Widerstand nur einen Teil
ihrer Energie abgeben sollen?
4. Woher "wissen" die Elektronen, welchen Anteil
ihrer Energie sie am ersten Widerstand abgeben sollen, damit für
den zweiten Widerstand der richtige Anteil entfällt? Im korrekten
Modell vermitteln die fließenden Elektronen nur eine
Energiezufuhr an den jeweiligen Widerstand aus dem
elektromagnetischen Feld. Die Energiezufuhr ergibt sich aus
der am Widerstand liegenden Spannung U und der durch ihn
fließenden Stromstärke I (E = q·U = I·U·Δt). Sie brauchen nicht
von "Anfang an" alle ihre Energie mitbekommen haben, die sie dann
vermeintlich stückweise in verschiedenen Bauteilen hinterlassen.
c) Widerstände R1, R2, ...
seien parallel geschaltet und mit einer Stromquelle der Spannung U
verbunden. Es fließen die Ströme I1, I2, ...
. In der Zeiteinheit Δt transportieren sie durch die Widerstände
die Ladungsmengen q1 = I1·Δt,
q2 = I2·Δt,
... und vermitteln den Transport der Energiemengen E1,
E2, ... zu den Widerständen.
Es ist sicher richtig, dass dann an den Widerständen die
Spannungen U1 = E1/q1, U2
= E2/q2, ... liegen. Aber diese
Spannungen sind alle gleich, unabhängig von den
Widerständen! Warum?
Fälschliche Argumentation mancher didaktischer
Modelle:
Wenn die Elektronen die
Energie "mit sich" herumtragen würden, wenn
also die übertragene Energie vorher in den Elektronen
lokalisiert wäre, wäre die Erklärung einfach: Jedes Elektron
würde in der Stromquelle (Energiequelle) die gleiche Energie ΔE
erhalten. Beim Durchgang durch einen der beiden
Widerstände würde es diese Energie teilweise abgeben. Würden n1
Elektronen im Zeitintervall Δt durch
den Widerstand R1 fließen, würden sie dort die
Energie E1 = n1·ΔE
hinterlassen. Dabei fließt die Ladungsmenge q1
= n1·e
und die Energie pro Ladungsmenge E1/q1
wäre gleich ΔE/e, also auch gleich
der Spannung U1 der
Stromquelle. Entsprechendes gilt für den Widerstand R2.
Die Spannungen an parallel geschalteten Widerständen sind
alle gleich und in unserem Fall gleich der Spannung
U der Stromquelle.
Diese Überlegung liegt letzten Endes allen
didaktischen Modellen zugrunde, die von in Ladungen
lokalisierter Energie ausgehen, ob diese Energie nun in
"Rucksäcken" von "Männchen" transportiert wird oder als
potenzielle Energie, ob sie nun Rucksack-Modell oder
Biene-Nektar-Modell oder Stäbchen-Modell heißen.
Argumentation der Physik:
Leider tragen Elektronen im Stromkreis die betreffende Energie nicht "mit sich herum"; bewegte Elektronen vermitteln nur den Energietransport in die Widerstände hinein. Wir wissen ja: In der Regel - nicht nur bei Wechselstrom - erreichen die Elektronen in den Widerständen nie die Strom-/Energie-Quelle, wenigstens nicht in der Beobachtungszeit. Sie könnten dort keine Energie "abholen". Der Energietransport erfolgt stattdessen gemäß des Energiestromdichte-Vektors S prop. E x B durch das elektromagnetische Feld in der Umgebung des stromführenden Leiters fast ohne Zeitverzögerung, "mit Lichtgeschwindigkeit". (Für S bzw. B ist der Strom eine Voraussetzung.)
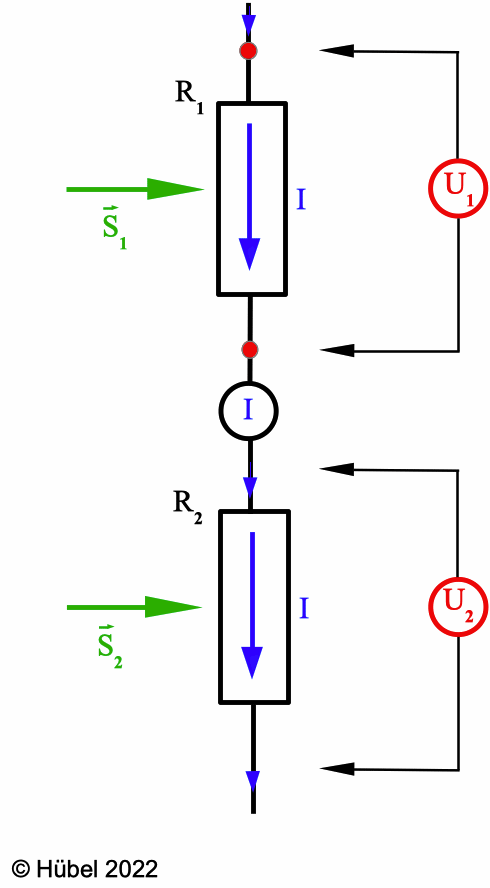 |
Ladungstransport durch einen
Strom I (blau) und Energietransporte (grün) in
den jeweiligen Widerstand durch den Raum unter Vermittlung
der bewegten Ladungen. Ein Strom mit der Stromstärke I fließt durch beide Widerstände R1 und R2. Zwischen zwei Punkten (rot) an Anfang und Ende des ersten Widerstands liegt die Spannung U1, entsprechend U2. I und U1 bzw. I und U2 und die Zeitdauer Δt des Energietransports bestimmen die längs der Energiestromdichte-Vektoren S1 bzw. S2 in die Widerstände übertragenen (elektromagnetischen) Energien. |
Durch die erwähnten didaktischen Modelle werden leider Lernhindernisse aufgebaut, z.B. für ein Verständnis des Energietransports mittels Wechselstrom.
Aber eine Kenntnis, von wo bis wohin
Elektronen Energie transportieren, ist gar nicht notwendig.
Es genügt zu wissen, dass jedes Elektron den gleichen
Energietransport ΔE "vermittelt";
keines ist im Stromkreis vor den anderen ausgezeichnet. Wenn
n Elektronen in der
Zeit Δt aus der
Strom-/Energiequelle heraus fließen, vermitteln sie den
Transport der Energie ΔE·n
und die Ladung q = e·n in den Stromkreis. Die
Spannung der Strom-/Energiequelle ist
also U = ΔE/e. Wenn in einem Zweig der
Parallelschaltung n1
Elektronen in der Zeit
Δt mit der Ladung e·n1
fließen und die Energieübertragung ΔE·n1
vermitteln, liegt am Widerstand also die Spannung U1
= ΔE·n1/(e·n1)
= ΔE/e = U. Entsprechendes gilt für
den zweiten Zweig, also U1
= U2 = U,
unabhängig von den dort fließenden Strömen:
|
An parallel geschalteten Widerständen liegt die
gleiche Spannung. |
Grund ist letzten Endes die Energie- und die Ladungserhaltung.
Im korrekten Modell vermitteln die fließenden Elektronen nur eine Energiezufuhr zu dem jeweiligen Widerstand aus dem elektromagnetischen Feld.
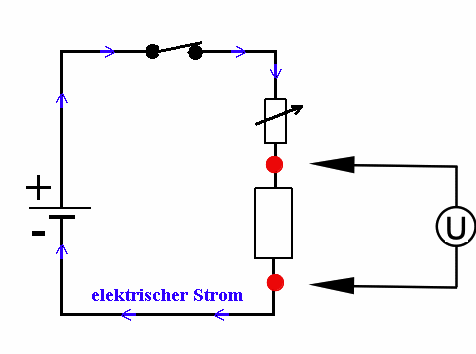 |
d) Wenn eine Spannung zwischen zwei Punkten gemessen werden soll, müssen die beiden Punkte durch einen Spannungsmesser (Voltmeter) verbunden werden. |
So lassen sich mit der Spannungs-Definition U = E/q bereits eine ganze Menge Eigenschaften von Stromkreisen anschaulich verstehen.
*) "abgeschlossen" heißt in diesem Fall: Elektrische Ladungen bzw. das Wasser können nicht aus dem Kreis entweichen, das Wasser also nicht aus den Rohren der Heizung. Das darf nicht verwechselt werden mit dem Begriff des "geschlossenen Stromkreises". Nur in einem geschlossenen Stromkreis kann überhaupt ein Strom fließen. Dadurch unterscheidet sich auch das Modell des "abgeschlossenen Heizungsstromkreises" von "Höhenmodellen", bei denen sich in Zwischenspeichern Wasser ansammeln, am Strom also nicht mehr teilnehmen kann, oder, von dort abfließend, wieder am Wasserstromkreis teilnehmen kann. Die potenzielle Energie, die beim Höhenmodell eine wesentliche Rolle spielt, spielt beim geschlossenen elektrischen Stromkreis keinerlei Rolle (vgl. Wasserschlauch-Modell).
Damit man bei der Induktion in einer bestimmten Situation in allen Bezugssystemen die gleiche Ringspannung erhält, kann es sinnvoll sein, in der Arbeit W auch einen Anteil von der Lorentz-Kraft zu berücksichtigen.
Die potenzielle Energie pro Ladungseinheit (W/q) wird Potenzial des Punktes P genannt, falls Wegunabhängigkeit gegeben ist. Dann liegt ein reines Potenzialfeld (wirbelfreies Potenzialfeld) vor. Im allgemeinen kann jedes beliebige elektrische Feld in ein wirbelfreies Potenzialfeld und ein potenzialfreies Wirbelfeld zerlegt werden.
Schulbücher vermeiden
häufig die Einführung einer Ringspannung, die z.B. bei
einem sich ändernden Magnetfeld in einer Spule entsteht.
Stattdessen sprechen sie von der gewöhnlichen "Spannung
zwischen den Enden der Spule". Warum sie das
machen, verstehen wir mit Hilfe der Ringspannung.
.
(September 2013; Ergänzungen Dezember 2022)