Eigenschaften eines Plattenkondensators

SG112 Eigenschaften eines Plattenkondensators

^© H. Hübel Würzburg 2013

Definition der Kapazität eines Kondensators

Mehr hierzu:

NEU Physikalische Schülerversuche mit PC und Mikroprozessor, 2. erweiterte Auflage, im Buchhandel erschienen

Abb. 1a: Eine mögliche Schülerversuchsanordnung zur Untersuchung der Eigenschaften eines Plattenkondensators.

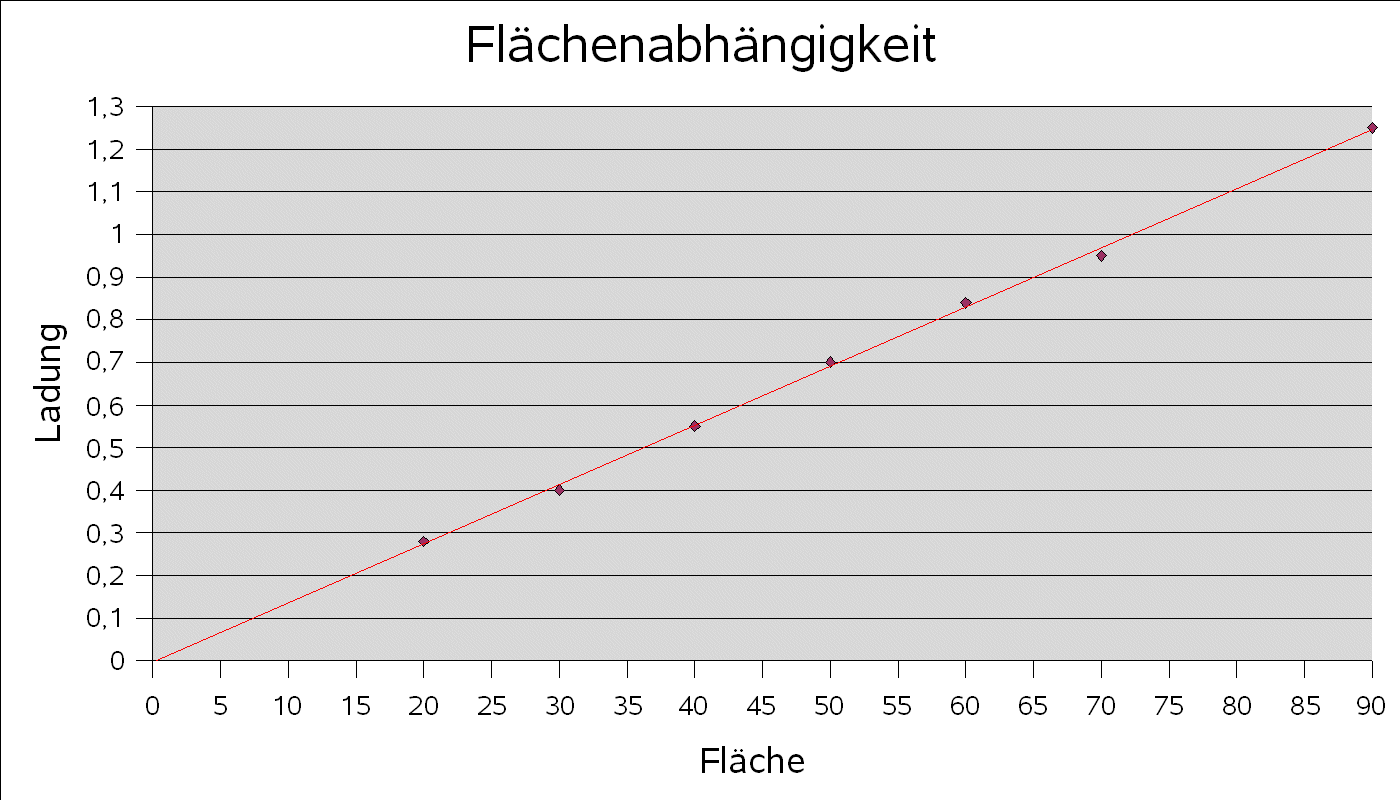
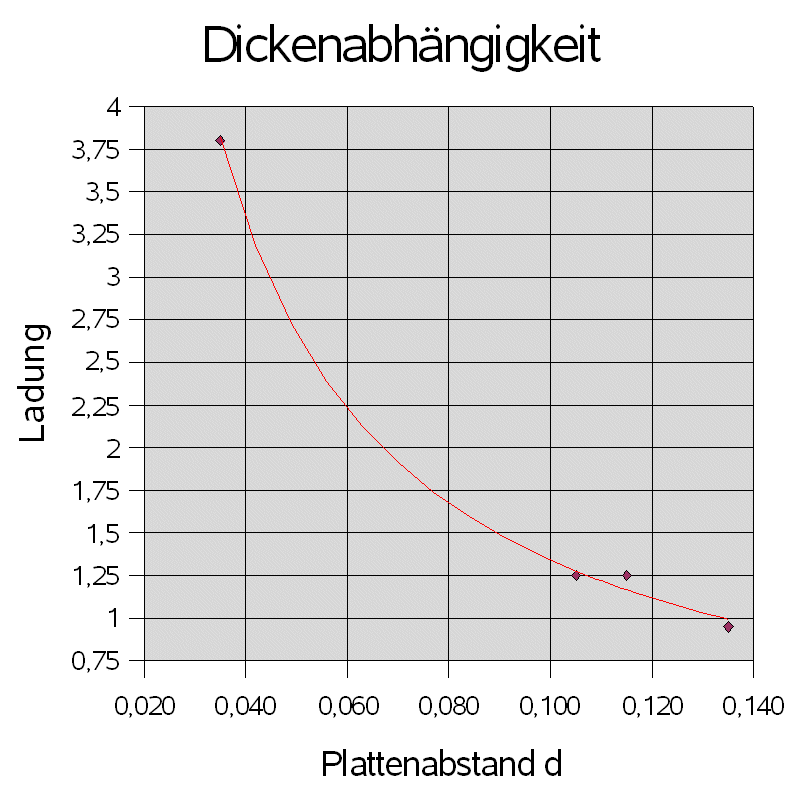
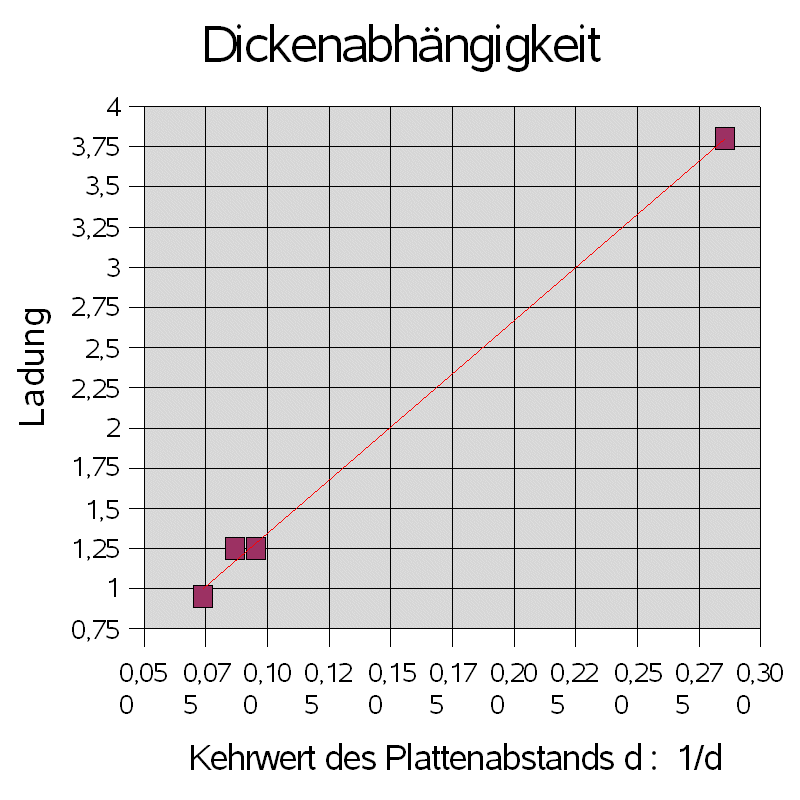
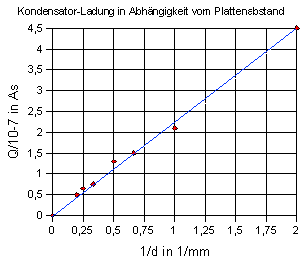
Als Plattenkondensator werden Folienkondensatoren mit unterschiedlichen Flächen A und Platten-Abständen d eingesetzt, die mit Hilfe von selbstklebenden Alu-Folien aus dem Baumarkt hergestellt werden können. Die Leimschicht dient als Isolator, es können auch zusätzlich unterschiedlich dicke Folien vom Tageslichtprojektor zwischen die Alu-Folien geklebt werden. Zwei Leimschichten direkt aufeinander => doppelter Plattenabstand.

Der Ladungsmesser wird gemäß der Schaltung unten auf einer Leybold-Rastersteckplatte aufgebaut.

Im Foto links ist das etwas anders gemacht:

In der Röhre befindet sich der unten beschriebene batteriebetriebene Ladungsmesser und Leuchtdioden, die das Vorzeichen der Ladung anzeigen (rot oder grün). Außerdem stellt er eine Ladespannung zur Verfügung (roter Stecker; blauer Stecker gemeinsame Masse).

.
Abb. 1b: Variante auf der Leybold-Rastersteckplatte

Ergebnisse:

Abb. 2: Flächenabhängigkeit der gespeicherten Ladung und der Kapazität C (da die Ladespannung immer gleich ist).

Es kommt hier nur auf die Proportionalität an, nicht auf die absoluten Werte von Q bzw. C.

Abb. 3: Abhängigkeit der Ladung bzw. Kapazität vom Plattenabstand. Leider standen hier nur 4 verschiedene Plattenabstände zur Verfügung. (ca. d = 0,054 mm wäre mit zwei direkt aufeinander geklebten Leimschichten leicht erreichbar gewesen.)

Auch im günstigeren Fall würde der Graph nur sagen: Die Kapazität sinkt mit zunehmendem Plattenabstand.

Abb. 4a: Abhängigkeit der Ladung bzw. Kapazität vom Plattenabstand. Mehr Messpunkte wären wünschenswert.

Bei der Auftragung von Ladung bzw. Kapazität gegenüber 1/d folgt aber einigermaßen glaubhaft eine direkte Proportionalität zwischen C und 1/d.

Abb. 4b: Abhängigkeit der Ladung bzw. Kapazität vom Plattenabstand - anderes Messbeispiel

Der Versuch zeigt:

C prop. A/d

Die Ermittlung der Proportionalitätskonstanten (elektrische Feldkonstanten) ε₀ = 8,8542 ·10^-12 C/(V·m) = 8,8542 ·10^-12 A·s/(V·m) erfordert eine Messung mit absoluten Größen.

Anhang:

Abb. 5: Ladungsmesser (elektronisches Elektroskop), geeignet für Schülerversuche:

Die Schaltung ist als Integrator bekannt. Erläuterung auch im oben genannten Buch.

Anders als bei Ladungsmessern, die auf einer Elektrometer-Schaltung beruhen, werden alle am Eingang (E1) angebotenen Ladungen auf den Kondensator C gepumpt. Dessen Ladespannung wird dann verlustlos am Ausgang gemessen und ist ein Maß für die hineingeflossene Ladung.

(C in der Größenordnung von 2 -10 nF. Als Operationsverstärker könnte ein OV mit extrem großen Eingangswiderstand und möglichst kleinem Offset-Strom verwendet werden, z.B. CA3140.)

Mit dieser Schaltung lassen sich gerade noch Ladungen in der Größenordnung von wenigen nAs messen.

Wenn C = 1 µF ist der Ladungsmesser für größere Ladungsmengen geeignet.

Ein Auflageblatt für die Leybold-Rastersteckplatte findest du hier.

hier

( Juni 2014 )