| ΔW = F||·Δs |
|
SG018 (Verschiebungs-)Arbeit ©
H. Hübel Würzburg 2013
|
Impres-sum |
Betrachte den einfachsten Fall: Du ziehst mit einer immer konstanten Kraft F an deinem zunächst ruhenden Mäppchen auf dem Tisch (parallel zum Tisch). Unter der Einwirkung der Kraft wird das Mäppchen beschleunigt, also immer schneller. Das würde so weitergehen, wenn nicht eine Reibungskraft entstünde, die das Beschleunigen zu hemmen sucht. Bei sehr hohen Geschwindigkeiten (die du auf dem Tisch nicht erreichen kannst) müsstest du die gesamte Kraft F nur zur Überwindung der Reibung aufwenden. Das Mäppchen hätte die maximal mögliche und damit konstante Geschwindigkeit erreicht.
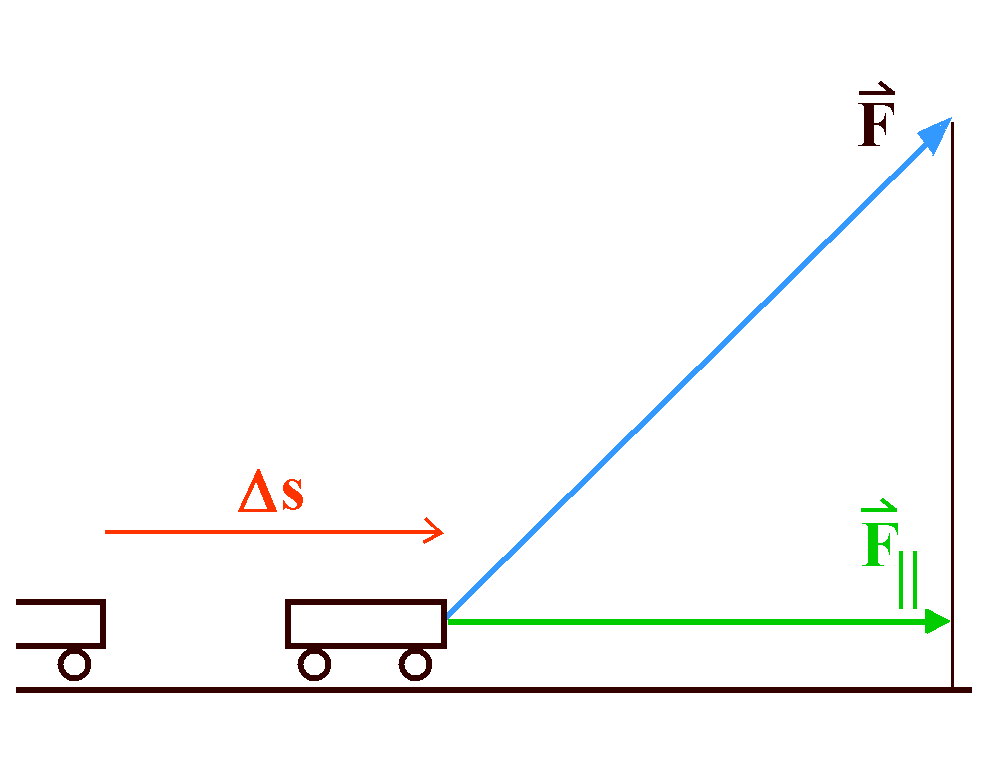
Wenn unter der Wirkung der Kraft F ein Körper um eine Strecke Δs in Richtung dieser Kraft verschoben wird, dann sagt man, es sei "eine Verschiebungsarbeit ΔW = F·Δs verrichtet" worden (F Betrag der Kraft F).
| ΔW = F·Δs |
Die Einheit der Arbeit ist [W] = 1 N·m
Beachte: I.A. stimmen Kraftrichtung und Bewegungsrichtung nicht überein!
Im Mäppchenbeispiel ist diese Verschiebungsarbeit ΔW genutzt worden, um das Mäppchen zu beschleunigen und um die Reibung zu überwinden. Verschiebungsarbeit heißt sie, weil dabei das Mäppchen um die Strecke Δs verschoben wurde. Wenn du im Winter einen Schlitten ziehen würdest, würde sich dieser horizontal "verschieben", aber du würdest schräg nach oben an einer Leine ziehen. Auch der Fall lässt sich auf die Definition zurückführen. F wäre dann die Komponente der Kraft, die in Richtung der Verschiebung wirkt, nennen wir sie mal F||.
 |
Die Komponente der Kraft F|| in
Richtung der Verschiebung Δs geht in die Verschiebungsarbeit
ein:
|
Für eine Verschiebungsarbeit ≠ 0 brauchst du zwei Bedingungen:
Die Definitionsformel gilt zudem nur, wenn die Kraft F konstant ist.
Wenn ein Gleiter auf der horizontalen Luftkissenfahrbahn quasi reibungsfrei gleitet, wird keine Verschiebungsarbeit verrichtet, obwohl sich der Gleiter "verschiebt", weil es keine Kraft in Richtung der Verschiebung gibt; die Gewichtskraft wirkt erstens senkrecht zur Verschiebung und zweitens wird sie durch eine Kraft vom Luftkissen auf den Gleiter aufgehoben.
Wenn du deine Schultasche in konstanter Höhe mit ausgestreckten Armen halten willst, ist das sehr anstrengend. Aber es wird dabei im Idealfall keine Verschiebungsarbeit verrichtet, weil dabei keine Verschiebung vorliegt. Die Muskeln verrichten dabei natürlich eine beträchtliche Arbeit. Aber das ist keine Verschiebungsarbeit.
Auch die Reibungskraft allein verrichtet eine Verschiebungsarbeit, wenn ein schnell bewegter Körper durch sie gebremst wird. Du weißt ja, die Reibungskraft ist immer entgegengesetzt zur Bewegungsrichtung, also auch zur Verschiebung Δs.
Statt Verschiebungsarbeit sind auch andere Namen in Gebrauch: Arbeit, mechanische Arbeit, Arbeit im physikalischen Sinn. Ich empfehle der Klarheit wegen die Bezeichnung Verschiebungsarbeit um sie von anderen Arbeiten zu unterscheiden.
Manchmal erwähnt man auch den Zweck der Arbeit im Namen: Beim Beschleunigen eines Körpers soll Beschleunigungsarbeit verrichtet werden, beim Spannen oder beim Zusammendrücken einer Feder Spannarbeit, beim Heben eines Körpers Hubarbeit, die Reibungskraft soll Reibarbeit verrichten. Ich halte es nicht für besonders sinnvoll, solche Bezeichnungen zu verwenden. Verschiebungsarbeit (zum Beschleunigen, zum Heben, ... ) genügt meines Erachtens.
.
Was macht man aber, wenn die Kraft nicht konstant ist?
Vielleicht kennst du den Trick schon: Man teilt den Vorgang auf in lauter kleine Stücke Δs, die so klein gewählt sind, dass in ihnen die Kraft F quasi konstant ist. Für jeden solchen kleinen Abschnitt kann man die Definitionsformel für ΔW anwenden. Um jetzt für eine Verschiebung s von einem Punkt P1 zu einem Punkt P2 die gesamte Arbeit zu ermitteln, muss man die vielen kleinen Beiträge ΔW zu W aufsummieren.
Das Spannen einer Feder soll das erläutern. Hier ist die Kraft nach dem Hooke'schen Gesetz proportional zur Verschiebung s (aus der Ruhelage) bzw. der Dehnung s. Die Zeichnung zeigt das Verfahren für eine bestimmte Breite Δs der einzelnen Abschnitte ("Streifenbreite"). Die gesamte Summe der Teilbeiträge ΔW entspricht der Fläche unter der Treppenfunktion. Wenn man jetzt die Streifenbreite Δs gegen 0 streben lässt, nähert sich die Treppenfunktion immer mehr der Geraden an, die Summe über die Teilbeiträge ΔW immer mehr der Dreiecksfläche unter der Geraden.
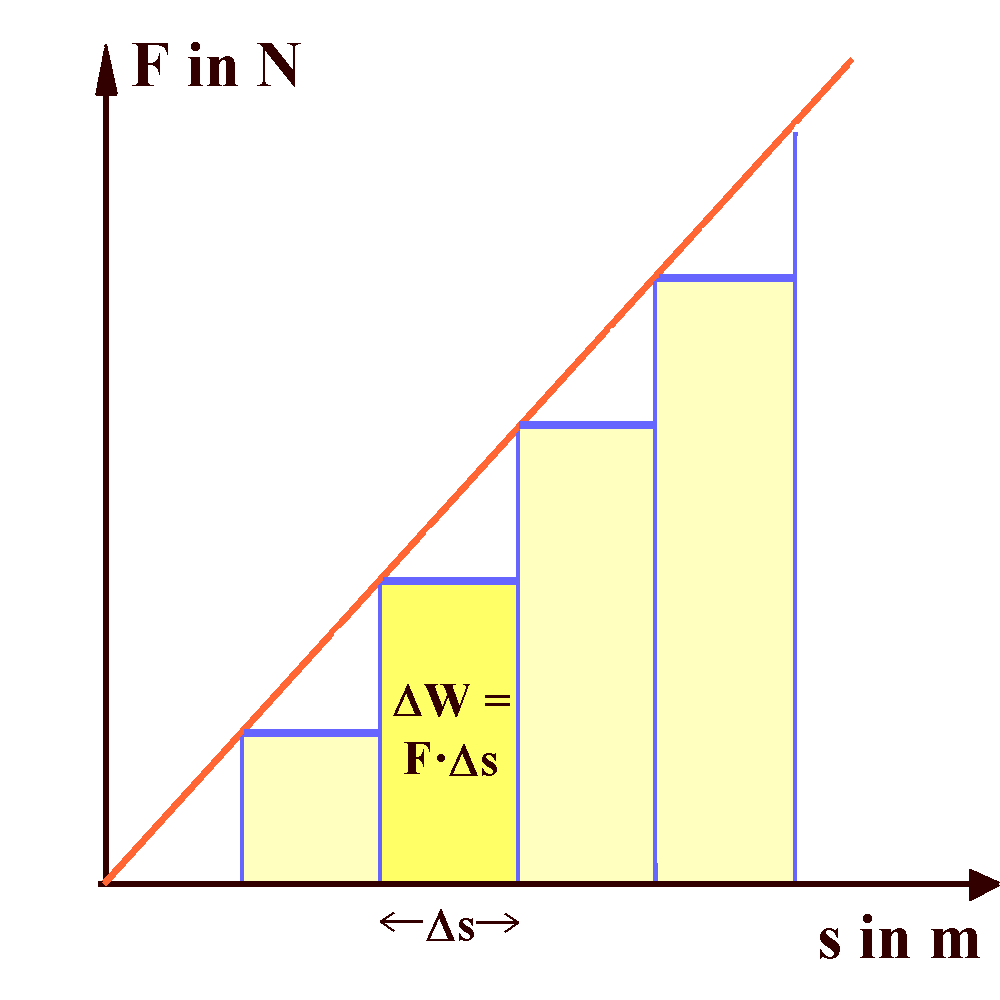 |
Das s-F-Diagramm für das Dehnen einer Feder gemäß
des Hooke'schen Gesetzes (F = D·s).
Die Dehnung s wird aufgeteilt in lauter (beliebig breite) Abschnitte der Breite Δs, in denen die Kraft näherungsweise konstant ist. Das wirkliche s-F-Diagramm wird angenähert durch eine Treppenfunktion (blau). Für jeden Abschnitt kann die Definitionsformel ΔW = F·Δs angewendet werden. Insgesamt wird näherungsweise die Arbeit verrichtet, die der schraffierten Fläche entspricht.
|
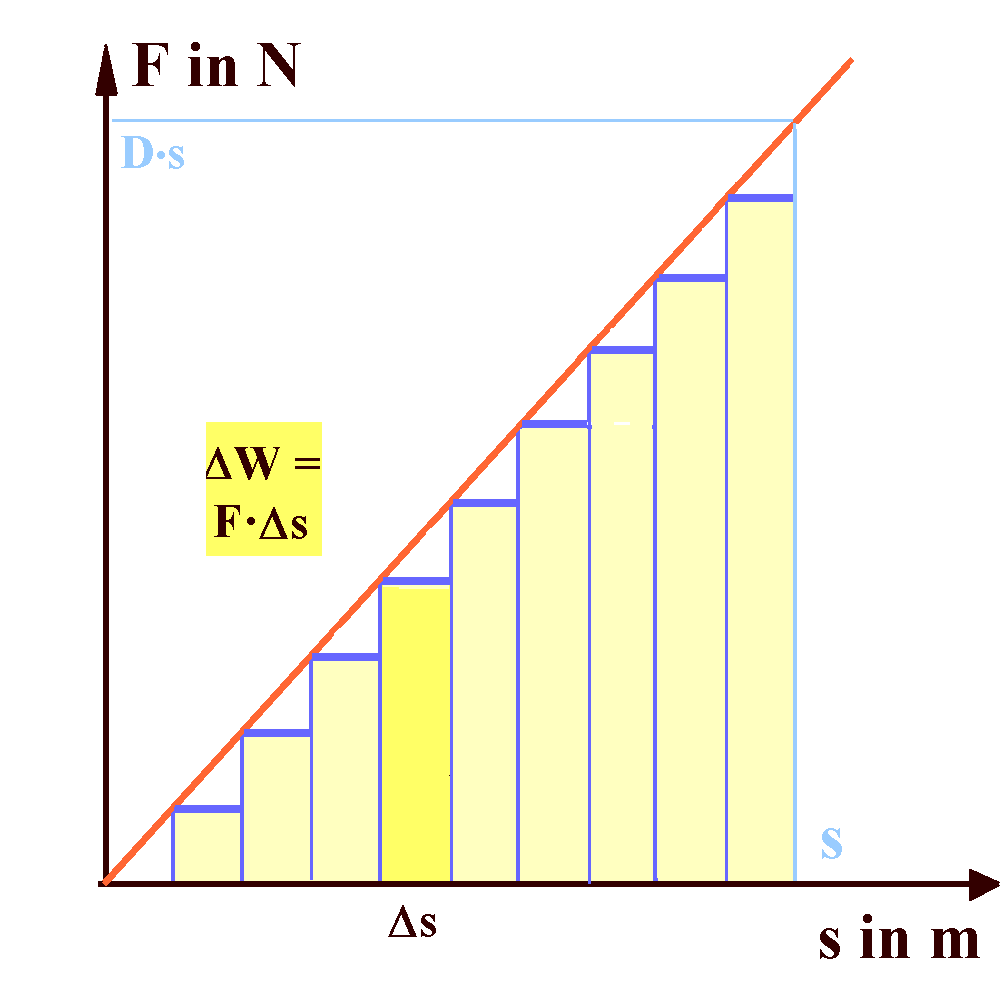 |
Verringert man die Streifenbreite, nähert sich
die Treppenfunktion immer mehr der Geraden des wirklichen
s-F-Diagramms an.
Je geringer die Streifenbreite Δs, desto mehr stimmt die schraffierte Fläche unter der Treppenfunktion mit der Dreiecksfläche unter dem wirklichen s-F-Diagramm überein. Im Grenzübergang Streifenbreite gegen 0 ergibt sich als Grenzfall für die verrichtete Arbeit ein Wert, der der (Dreiecks-)Fläche unter dem s-F-Diagramm entspricht: W = ½·D·s2 |
Es ergibt sich hier also
| W = ½·D·s2 |
.
Ähnlich kommt auch die Gesetzmäßigkeit für die Verschiebungsarbeit beim Beschleunigen eines Körpers aus der Ruhe auf die Geschwindigkeit v zustande:
| W = ½·m·v2 |
.
Außer der Verschiebungsarbeit gibt es in der Physik andere Arbeiten, z.B. Wärmearbeit oder kurz Wärme Q beim Erwärmen eines Körpers. Durch Arbeit wird die Energie eines Körpers oder Systems erhöht oder vermindert.
Wenn am Anfang eines Vorgangs die Energie eines Körpers E1 ist und am Ende E2, hat sich also die Energie um ΔE = E2 - E1verändert. Diese Energiedifferenz ist gleich der dabei (von außen) verrichteten Arbeit W. Wenn nach dem Vorgang eine größere Energie E2 vorhanden ist (E2 > E1) wurde (von außen) positive Arbeit W verrichtet, wenn nach dem Vorgang eine geringere Energie E2 vorhanden ist (E2 < E1), wurde (von außen) negative Arbeit "verrichtet", also Energie abgegeben.
(Wir könnten jetzt auch sagen, dass der Körper positive Arbeit an seiner Umgebung verrichtet hat.)
Das ist z.B. bei einem Bremsvorgang der Fall. Durch Reibungsarbeit wird einem bewegten Körper kinetische Energie entzogen, die als innere Energie in den reibenden Körpern (z.B. Fahrzeug und Unterlage) noch vorhanden ist.
Statt 1 N·m kann man wie bei der Energie auch 1 J (ein Joule, "dschuul" gesprochen") sagen, also 1 N·m= 1 J.
( Oktober 2013 )