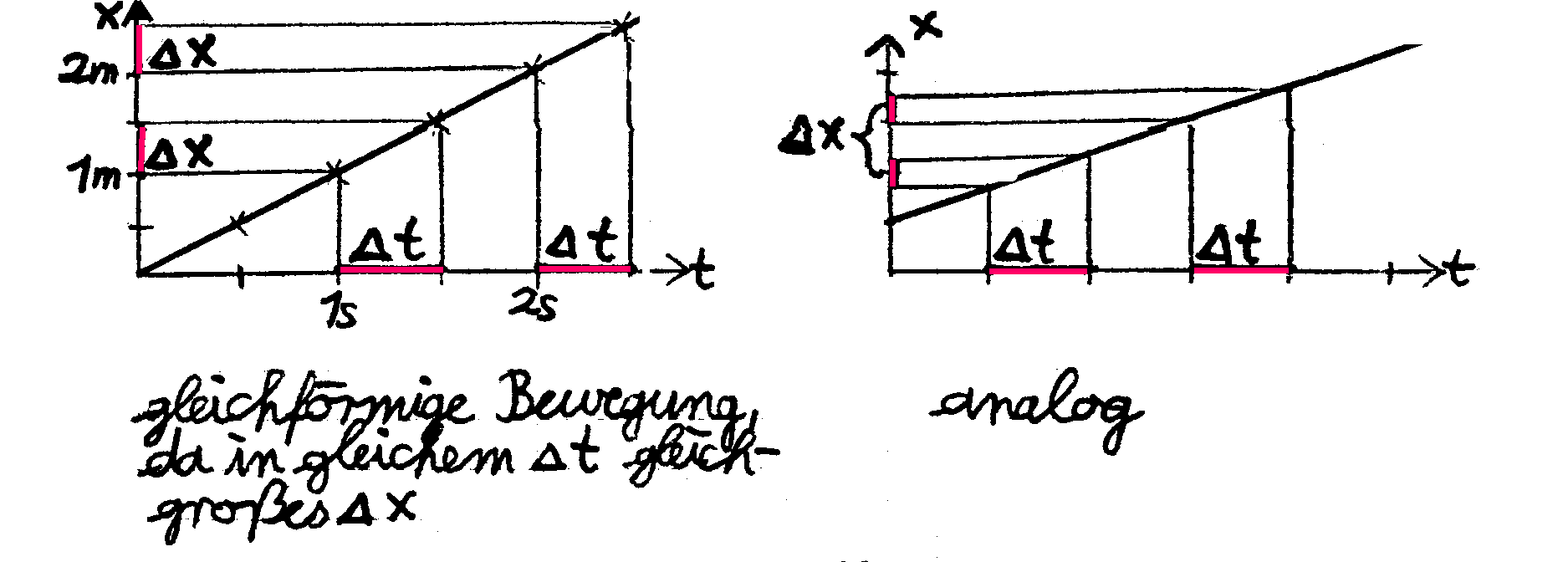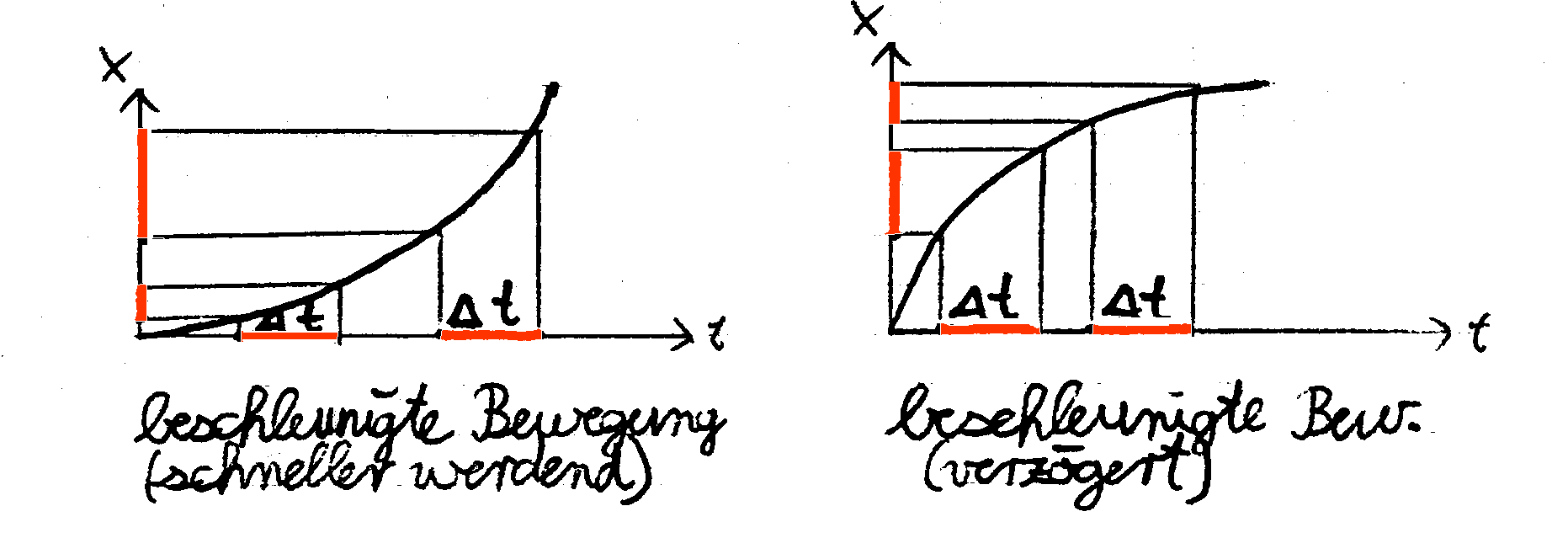Aber bis ins 14. Jahrhundert hinein konnten die Wissenschaftler Bewegungen nur mit den Begriffen "schneller" oder "langsamer" beschreiben. Der Fortschritt kam durch einen Wissenschaftler, der auch Bischof in Frankreich war, Nicolas von Oresme. Er schlug - mit heutigen Worten - vor, den Ort in Abhängigkeit von der Zeit quantitativ zu untersuchen und das Ergebnis in einem t-x-Diagramm darzustellen. Der französische Mathematiker und Philosoph Descartes (lat. Cartesius) baute ca. 300 Jahre später dieses Programm aus, und so heißt heute ein rechtwinkliges Koordinatensystem Kartesisches Koordinatensystem.

Ein solches Koordinatensystem, das zur Beschreibung von Bewegungen geeignet ist, kann im Klassenzimmer konstruiert werden. Dazu sollst du dich im Klassenzimmer hin und her bewegen. Zur Vereinbarung eines solchen Koordinatensystems und zur Registrierung von Bewegungen hat sich ein Sonarmeter bewährt zusammen mit einem PC und einem geeigneten Programm (z.B. SONAR.EXE). Es gibt eine Variante.

Ein Sonarmeter funktioniert wie ein "elektronischer Zollstab", den manchmal Schreiner verwenden. Ein Ultraschall-Lautsprecher senden einen Ultraschallimpuls aus, der am sich bewegenden Gegenstand reflektiert wird und dann von einem Mikrophon aufgenommen wird. Aus der Laufzeit des Ultraschallimpulses hin und zurück errechnet der PC die momentane Entfernung des Gegenstands vom Sonarmeter. Dazu muss das Programm die Ausbreitungsgeschwindigkeit des Schalls kennen. Das Programm zeigt dann auf dem Bildschirm des PCs die Entfernung in m an. Um ein Koordinatensystem im Raum zu vereinbaren, muss man einen Koordinatenursprung und die positive Koordinatenrichtung willkürlich, aber eindeutig festlegen. Maßstäbe für Ort und Zeit muss das Programm auch kennen. 1. Vereinbarung des Koordinatenursprungs Irgendeine Position von dir, die du beliebig wählst (im Strahl des Sonarmeters, aber mit einem genügenden Abstand zum Sonarmeter) wählst du als Koordinatenursprung. Nach einem bestimmten Tastendruck registriert das Programm diese Position als Koordinatenursprung. Du siehst das daran, dass auf dem Bildschirm 0 m angezeigt wird, solange du dich im Koordinatenursprung befindest. Du markierst die Position auf dem Boden. 2. Wahl der positiven Koordinatenrichtung Die ist zunächst vom Sonarmeter weg festgelegt. Du kannst sie aber durch Tastendruck auch umkehren. 3. 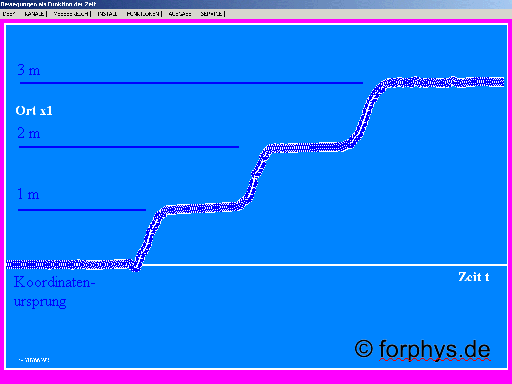Konstruktion des Koordinatensystems im Raum Du bewegst dich jetzt in eine Position mit der Bildschirmanzeige 1 m und markierst diese Position auf dem Boden. Dann gehst du in eine Position mit der Anzeige 2 m und markierst wieder, usw. 4. Negative Orte? Geh' nun zum Koordinatenursprung zurück. Auf dem Bildschirm wird 0 m angezeigt. Geh' nun weiter über diesen Punkt hinweg. Auf dem Bildschirm werden negative Orte angezeigt. Je weiter du dich entgegengesetzt zur positiven Richtung über den Koordinatenursprung hinweg bewegst, desto "negativer" wird die Anzeige. Markiere auf dem Boden den Punkt mit der Anzeige   - 1 m. Negative Orte bedeuten also Orte jenseits des Koordinatenursprungs, die erreicht werden, wenn du dich in negative Richtung (entgegengesetzt zur vereinbarten positiven Richtung) bewegst. 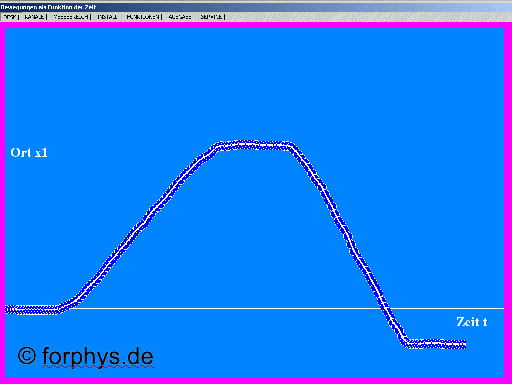Du erhältst eine Reihe von Marken auf dem Boden, die die Koordinatenachse im Raum und positive und negative Orte (Ortskoordinaten) anzeigen. Da wir uns auf eine Dimension beschränken, nennen wird die Ortskoordinaten x.

Wie du den Koordinatenursprung und die positive Koordinatenrichtung gewählt hast, ist weitgehend belanglos. Du könntest sie für einen anderen Versuch ändern. Sie muss aber eindeutig sein, damit du eine bestimmte Bewegung beschreiben kannst.

Wenn du dich jetzt längs der Koordinatenachse hin und her bewegst, zeigt das Sonarmeter sich ändernde positive oder negative Ortskoordinaten x an.

Das t-x-Diagramm Wenn nun das Koordinatensystem im Klassenzimmer durch Metermarken definiert ist, und wenn dem Sonarmeter deine Wahl des Koordinatenursprungs und der positiven Koordinatenrichtung  bekannt gemacht worden sind, wird das Sonarmeter auf Graphik-Darstellung umgeschaltet. Dann trägt es die jeweiligen Orte (Ortskoordinaten) in Abhängigkeit von der Zeit auf - nach oben den Ort x, nach rechts die Zeit t in willkürlichen Einheiten. Es wird eine relativ einfache Bewegung registriert: Ein Schüler läuft vor dem Sonarmeter und bleibt bei den jeweiligen Metermarken einige Zeit stehen. Links ist ein Beispiel des t-x-Diagramms einer solchen Bewegung dargestellt. Da du hoffentlich die Bewegung gesehen hast, fällt es dir nicht schwer, das Diagramm zu deuten. Du siehst klar, dass sich der Ort bei den Meterpositionen längere Zeit nicht verändert hat, dazwischen aber einigermaßen "gleichförmig".

Ein weiteres t-x-Diagramm kannst du wahrscheinlich schon deuten, ohne die Bewegung gesehen zu haben: Anfänglich ruhte der Schüler im Koordinatenursprung. Dann bewegte er sich "gleichförmig" (mit konstanter Geschwindigkeit) zu einem bestimmten Ort und blieb dort wieder eine Zeitlang in Ruhe. Anschließend bewegte er sich "gleichförmig" rückwärts zum Koordinatenursprung und sogar über ihn hinaus bis zu einem negativen Ort, an dem er in Ruhe bleibt.

Im Folgenden werden für verschiedene Bewegungen die Ortsänderungen Dx in aufeinander folgenden, aber jeweils gleich großen Zeitabschnitten Δt untersucht. Die Zeichnungen stammen aus einem Schülerheft.

In jeweils gleich großen Zeitabschnitten Δt  erfolgt die gleiche Ortsänderung Δx . Eine solche Bewegung heißt gleichförmige Bewegung.

In jeweils gleich großen Zeitabschnitten Δt  erfolgen hier unterschiedliche Ortsänderungen Δx . Eine solche Bewegung heißt beschleunigte Bewegung. Mit zunehmender Zeit werden die Ortsänderungen Δx links immer größer. Es handelt sich um eine schneller werdende (beschleunigte) Bewegung. Mit zunehmender Zeit werden die Ortsänderungen Δx rechts immer kleiner. Es handelt sich um eine langsamer werdende (beschleunigte) Bewegung.

Auch bei beliebigen Bewegungen im Raum muss man einen Koordinatenursprung festlegen. Der Ort wird dann durch einen Ortsvektor x gekennzeichnet. (Hier ist der Vektor durch Fettdruck gekennzeichnet. In Schreibschrift (wie in der Zeichnung) schreibt man über das Symbol x einen kleinen Pfeil, der immer nach rechts gerichtet ist.) Der Ortsvektor x geht vom Koordinatenursprung aus und hat seine Spitze am jeweiligen Ort. Bei der Bewegung eines Satelliten um die Erde (Bild links) wählt man am einfachsten den Koordinatenursprung im Zentrum der Erde. Der Ortsvektor ändert dann ständig seine Richtung (zum Satelliten hin), wenn der Satellit um die Erde kreist.

Variante: Mit einem Metermaß wird das Koordinatensystem im Raum konstruiert (positive - negative Orte)  ( zurück )