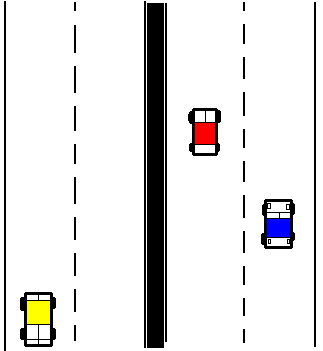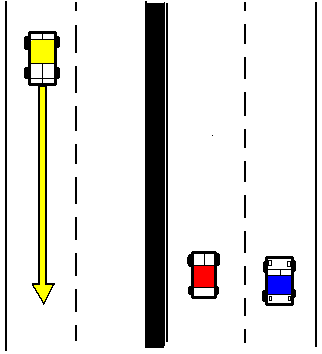
Hier siehst du zwei Momentaufnahmen einer befahrenen Autobahn zu zwei verschiedenen Zeiten, von einer Brücke herunter "fotografiert". Die Bewegungsrichtung wird durch einen Pfeil gekennzeichnet. Die Länge des Pfeils ist ein Maß dafür, wie schnell das Auto fährt, für die "Schnelligkeit" der Bewegung. Trage in die linke Zeichnung auch für die beiden übrigen Autos die Geschwindigkeitspfeile ein!
Zu einem bestimmten Zeitpunkt	0,1 s später

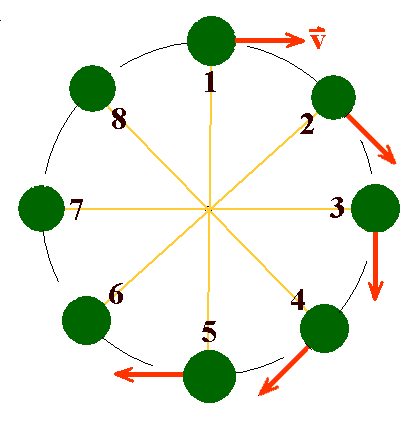
Eine Größe, die durch einen Betrag und eine Richtung gekennzeichnet ist, heißt in der Physik Vektor ^*). Hier entspricht der Betrag des Geschwindigkeitsvektors der "Schnelligkeit "der Bewegung und seine Richtung der Bewegungsrichtung. Den Betrag der Geschwindigkeit, also die "Schnelligkeit", nennt man oft auch Tempo (engl. speed). Beim Geschwindigkeitsvektor entspricht sie der Pfeillänge. Auch in vielen anderen Sprachen wird deutlich unterschieden zwischen Geschwindigkeit und Tempo, z.B. heißt Geschwindigkeit im Portugiesischen velocidade, dagegen Tempo rapidez. Man spricht von "Tempo 100" zur Schonung der Umwelt und von "Tempo-30-Zonen" zur Schonung von Fußgängern.

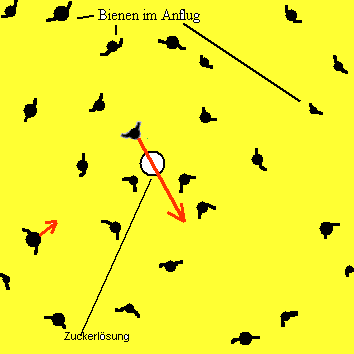	Bienen nähern sich einem Topf mit Zuckerlösung. Je näher sie an die Zuckerlösung herankommen, desto gieriger werden sie und desto schneller fliegen sie. Zeichne noch einige Geschwindigkeitsvektoren durch Pfeile ein!
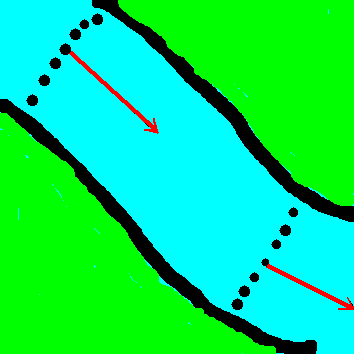	Wasserströmung in einem Fluss. Das Wasser strömt parallel zum Flussufer, in der Flussmitte am schnellsten. Ergänze weitere Geschwindigkeitsvektoren des strömenden Wassers durch Pfeile.

Pinocchios Nase zeigt bei einer Kreisbewegung die Bewegungsrichtung und damit die Richtung des Geschwindigkeitsvektors an!

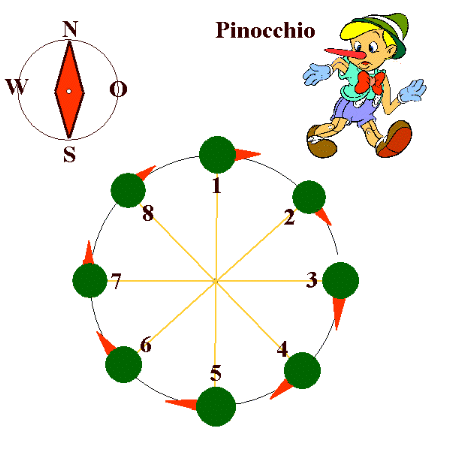	Pinocchio hat mal wieder eine lange Nase bekommen. Er rennt auf einem Kreis immer seiner roten Nase nach, in jedem Augenblick gleich schnell. Seine Bewegungsrichtung ändert sich ständig: In der Position 1 rennt er genau nach Osten, in der Position 2 nach SO, in der Position 3 nach S, in der ... . Statt der roten Nase könntest du zu jeder Position den Geschwindigkeitsvektor durch einen Pfeil in Bewegungsrichtung (in die die rote Nase zeigt) einzeichnen. Da sich  Pinocchio in jedem Augenblick gleich schnell bewegt, ist der Betrag des Geschwindigkeitsvektor zu jedem Zeitpunkt (in jeder Position) gleich groß: Alle Geschwindigkeitspfeile sind hier gleich lang.
	Einige der Geschwindigkeitsvektoren sind hier durch Pfeile eingetragen. Auch, wenn sich in jedem Zeitpunkt Pinocchio gleich schnell bewegt, so ändert sich doch ständig der Geschwindigkeitsvektor, weil sich seine Richtung ( = die Bewegungsrichtung) ändert. In diesem Fall sagt man auch kurz: die Geschwindigkeit ändert sich ständig. (An diese Sprechweise solltest du dich gewöhnen. Zwar bewegt sich Pinocchio zu allen Zeiten gleich schnell, aber weil der Geschwindigkeitsvektor ständig seine Richtung ändert, spricht man auch hier von einer Geschwindigkeitsänderung.)
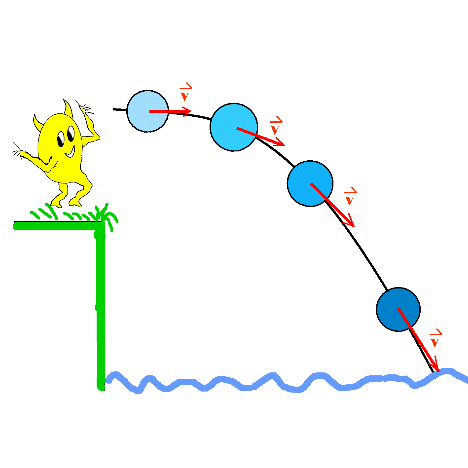	Von Klippen herunter wird ein Stein ins Meer geworfen. Der Stein wird  zunächst horizontal weggestoßen, bewegt sich dann aber unter der Wirkung der Gewichtskraft auf einer gekrümmten Bahn nach unten. Es ändert sich die Bewegungsrichtung und auch der Betrag der Geschwindigkeit: Die Pfeile, die die Geschwindigkeitsvektoren v kennzeichnen, weichen immer stärker von der horizontalen Richtung ab und werden im Laufe der Bewegung immer länger.

Bei eindimensionalen Bewegungen (also längs einer Geraden) wird die Beschreibung sehr einfach. Man stellt sich ein Koordinatensystem vor, das man so orientiert, dass die Bewegung in x-Richtung oder entgegengesetzt dazu erfolgt.

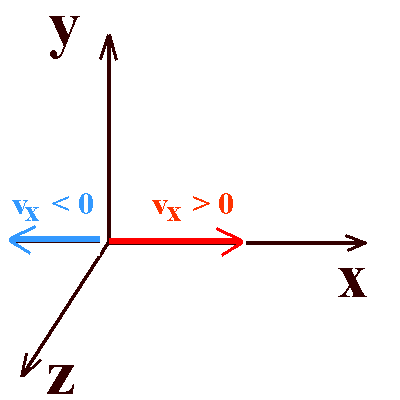Dann kann man den Geschwindigkeitsvektor auch durch die x-Koordinate allein ausdrücken: vx oder kurz v. Wenn v (vx ) positiv ist, bewegt sich der Körper in positive x-Richtung, wenn v negativ ist, entgegengesetzt dazu, also in negative x-Richtung. Wenn v = 0, ruht der Körper. Bei eindimensionalen Bewegungen (längs einer Geraden) wird die Geschwindigkeitskoordinate vx bzw. v oft selbst als Geschwindigkeit bezeichnet. Tempo ist dann der Betrag von v.  Beim PKW kannst du das Tempo vom Tacho ablesen (eigentlich Tachometer), nicht in jedem Fall aber die Geschwindigkeit. Wann stimmt die Geschwindigkeit nicht mit dem Tempo überein? Die Geschwindigkeit kann bei eindimensionalen Bewegungen positiv, negativ oder 0 sein, Tempo kann als Betrag der Geschwindigkeit nie negativ sein.

Bis ins Mittelalter hinein wurden Bewegungen immer allein mit Hilfe der "Schnelligkeit" diskutiert. Das führte nicht weiter.

Erst im  14. Jahrhundert setzte sich die Gewohnheit durch, Bewegungen im Raum durch zeitlich veränderliche Ortskoordinaten eines Punktes und auch Geschwindigkeit(skoordinat)en zu beschreiben. Der französische Bischof Nicolaus von Oresme (ca. 1320 - 1382) gab hier entscheidende Anstöße. Und auch Galilei spielte eine wichtige Rolle, später dann im 17. Jahrhundert der französische Philosoph und Mathematiker Descartes.

Für uns ergibt sich damit die Frage, wie die Geschwindigkeit mit Ortskoordinaten zusammenhängt.

Hier noch eine Aufgabe, die du lösen kannst, ohne zu wissen, was Geschwindigkeit oder Tempo bedeutet. Hierzu brauchst du nur etwas gesunden Menschenverstand. Der ist in der Physik überhaupt recht nützlich.

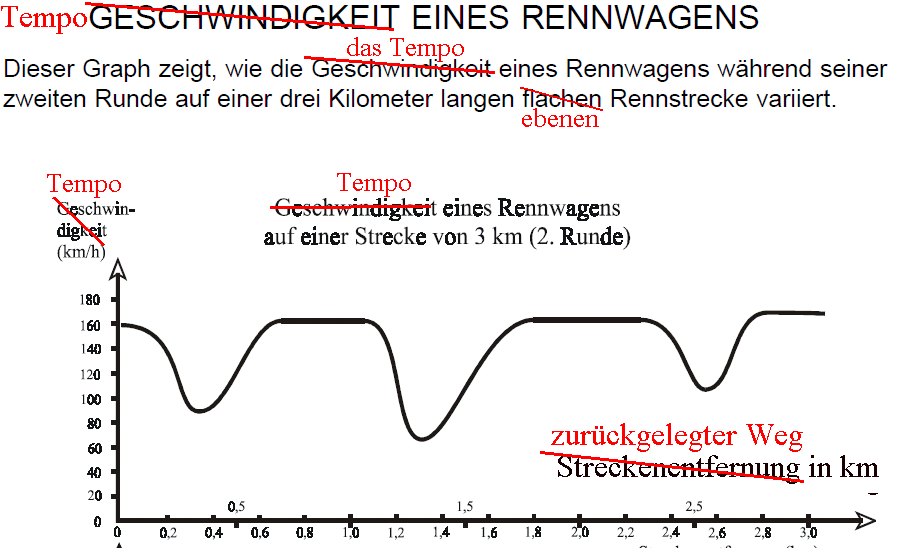Das ist eine Aufgabe aus dem PISA-Test 2000. Offenbar geht es hierbei nicht um den Geschwindigkeitsvektor. Die zugehörige (zweite) Aufgabe zeigt, dass es auch nicht um eine eindimensionale Bewegung längs einer Geraden handelt. Deswegen kann hier auch nicht die Geschwindigkeit im Sinne einer Geschwindigkeitskoordinate aufgetragen sein. Bei diesem Graphen kann also nicht die Geschwindigkeit dargestellt sein, sondern nur ihr Betrag bzw. das Tempo. "Streckenentfernung" ist auch kein physikalischer Begriff. Gemeint ist die zurückgelegte Weglänge seit dem Start. Mit etwas Nachdenken wärst du sicher darauf gekommen, wie die Aufgabensteller das gemeint haben. (Da hatten es übrigens englischsprachige Schüler etwas einfacher: Bei ihrer Formulierung der Aufgabe wurden ohne Übersetzungsfehler die richtigen Begriffe verwendet (speed / distance along the track !)

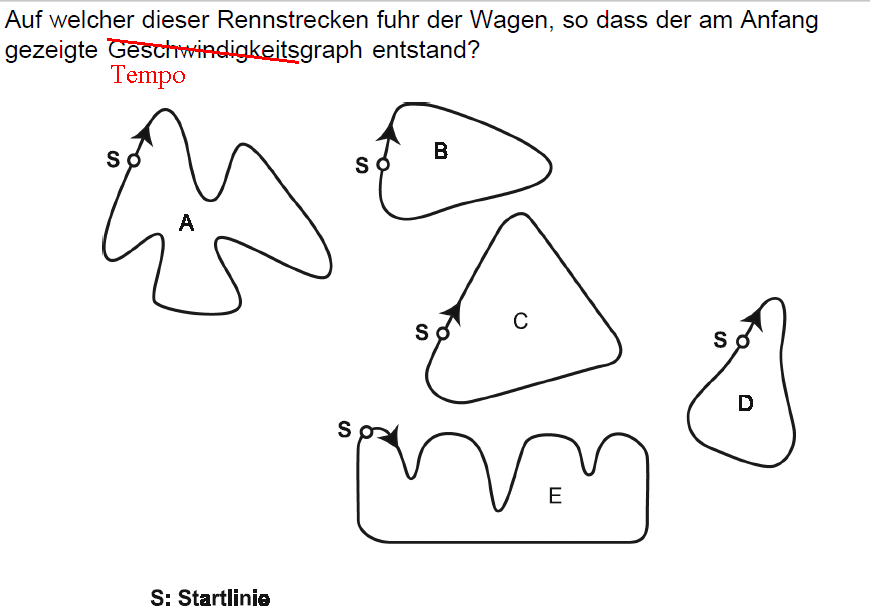Wie gesagt: Es geht hier nicht um Geschwindigkeit (velocity), sondern um deren Betrag bzw. um Tempo (speed). Zur Lösung könntest du dich fragen, was der Grund für ein Langsamerwerden sein könnte. Dann brauchst du dich nur noch zu fragen, ob diese Situation bei einer der gezeichneten Rennstrecken gleich häufig eintritt wie im Tempographen. Wie muss sich der Rennwagen in einer besonders engen Kurve verhalten? Dann musst du noch etwas darauf schauen, ob nach einer langen oder kurzen Wegstrecke diese Situation eintreten soll. Hast du die richtige Lösung herausgefunden?

Hinweis:

Zum  Gebrauch von Geschwindigkeit und Tempo in einigen anderen Sprachen:

deutsch	englisch	italienisch	französisch	portugiesisch
Geschwindigkeit	velocity	velocità	vitesse / (vélocité)	velocidade
Tempo ("Schnelligkeit")	speed	rapidità	vitesse / (rapidité)	rapidez

In dieses Kapitel flossen Anregungen ein, auf die ich vor vielen Jahren in einem Artikel von Wiesner und Wodzinski gestoßen bin.

.

.

( aktualisiert Oktober 2013 )