Vektoren

Wenn du eine Bewegung beschreiben möchtest, kannst du die Bewegungsrichtung und die "Schnelligkeit" der Bewegung (Tempo) angeben. Beide Angaben zusammen bestimmen den Geschwindigkeitsvektor: Die Bewegungsrichtung entspricht der Richtung des Geschwindigkeitsvektors und die "Schnelligkeit" (Tempo) seinem Betrag.

Ein Vektor ist in der Physik allgemein eine Größe, die durch Richtung und Betrag gekennzeichnet ist. Sie wird meist durch einen Buchstaben mit Pfeil darüber oder durch den fettgedruckten Buchstaben symbolisiert: Beim Geschwindigkeitsvektor ist v üblich (v wie das englische velocity). Für den Betrag nimmt man einfach v, ohne Fettdruck. Dafür gibt es einen eigenen Namen, Tempo (engl. speed).

Genauso ist eine Kraft ein Vektor, weil sie durch Betrag und Richtung gekennzeichnet ist ^*). Sie wird üblicherweise durch F symbolisiert. F kommt vom englischen Wort für Kraft, force; aber auch in vielen anderen Sprachen beginnt das entsprechende Wort mit f.

Die folgenden Ausführungen gelten, wenn die Kraft - idealisierend - an einem punktförmigen Körper angreift.

Beispiele für Kraftrichtungen

• Gewichtskraft beim Fall oder beim schrägen Wurf: senkrecht nach unten: Wir erkennen, dass sie vertikal nach unten gerichtet ist, weil ein Körper in diese Richtung beschleunigt wird, weil sie den geworfenen Körper nach unten zieht
• Positiv elektrisch geladene Kugel: Wo auch immer wir eine negative "Probeladung" in die Nähe der Kugel bringen, sie wird zum Zentrum der Kugel gezogen. So ist die elektrische Kraft gerichtet.
• Reibungskraft: sie bremst einen bewegten Körper, verändert nicht seine (Geradeaus-)Bewegungsrichtung, aber macht ihn langsamer. Sie zieht entgegengesetzt zur Bewegungsrichtung.
• Federkatapult für einen Fahrbahn-Gleiter: Die Kraft beschleunigt den Gleiter längs der Fahrbahn und ist also längs der Fahrbahn gerichtet.  
• Ruhende Kugel, die auf einer geneigten Ebene losgelassen wird. Es entsteht eine Handabtriebskraft in Richtung des stärksten Gefälles, nach unten.
• Kugel, die auf einer geneigte Platte schräg nach oben hochgeschossen wird. Die gleiche Hangabtriebskraft wirkt nach unten und sorgt für eine Richtungsänderung.

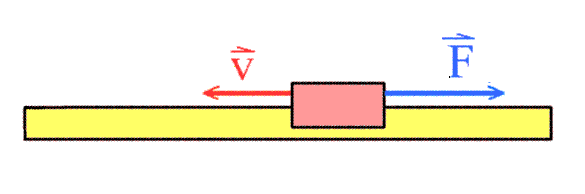
Das kennst du schon von eindimensionalen Bewegungen, z.B. längs einer Fahrbahn. Hier kann eine Kraft in Bewegungsrichtung wirken; dann beschleunigt sie den Wagen (macht ihn schneller). Oder sie kann entgegengesetzt zur Bewegungsrichtung wirken; dann bremst sie den Wagen.  

Wie bei der Reibung immer sind hier Kraft F und Bewegungsrichtung v entgegengesetzt orientiert. Die Kraft F bremst den Körper ab.

Versuch: Auf- und ab an der schiefen Ebene

Ein Gleiter wird auf der geneigten Luftkissenbahn durch einen Stoß den Hang hinauf geschossen. Während er hochsteigt, wirkt die Kraft, die Hangabtriebskraft. Sie wirkt wie es der Name sagt. Sie ist aus der Gewichtskraft entstanden, die auf den Gleiter wirkt. Während nun der Gleiter sich hangaufwärts bewegt, wirkt die Hangabtriebskraft entgegengesetzt zur Bewegungsrichtung und bremst den Gleiter immer mehr ab, bis er schließlich zum Stillstand kommt. Aber auch dann wirkt noch die Hangabtriebskraft und beschleunigt den Gleiter in ihre Richtung, also hangabwärts. Der Gleiter erreicht seine dem Betrag nach maximale Geschwindigkeit, wenn er unten auf die Prallfeder stößt, bevor er wieder hoch katapultiert wird. Nur beim Stoß mit der Prallfeder entsteht eine nach oben gerichtete Kraft, die den Gleiter zunächst abbremst (Bewegungsrichtung und Kraft entgegengesetzt) und dann wieder aufwärts beschleunigt (Kraft und Bewegungsrichtung gleichorientiert). In den folgenden Zeichnungen ist nur die Wirkung der Hangabtriebskraft erläutert.

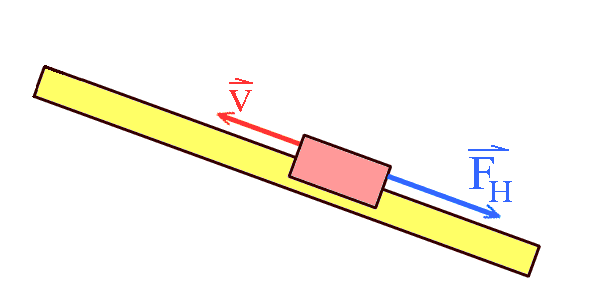	Ein Gleiter oder Wagen bewegt sich auf der geneigten Fahrbahn nach oben. Dabei wirkt die Hangabtriebskraft. Bei der Aufwärtsbewegung sind Kraft und Bewegungsrichtung entgegengesetzt. Die Hangabtriebskraft bremst den Wagen, allmählich bis zum Stillstand ab.
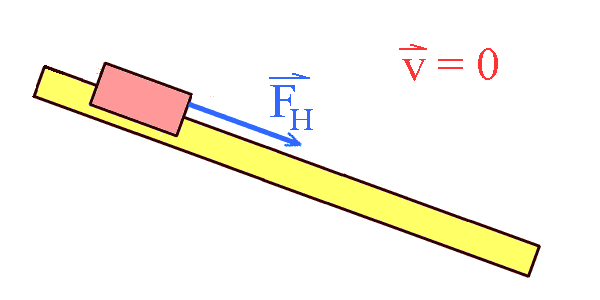	Der Gleiter oder Wagen hat seinen höchsten Punkt erreicht, wo er kurzzeitig zum Stillstand gekommen ist. Trotz Stillstand wirkt immer noch die Hangabtriebskraft. Die Hangabtriebskraft beginnt, den Wagen wieder nach unten zu beschleunigen.
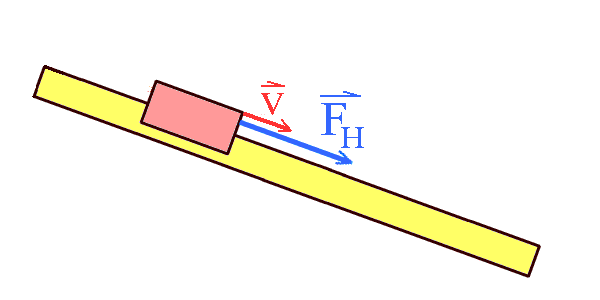	Der Gleiter oder Wagen bewegt sich wieder hangabwärts. Bei der Abwärtsbewegung sind Kraft und Bewegungsrichtung gleich gerichtet. Die Hangabtriebskraft beschleunigt den Wagen weiter nach unten..

Noch drastischer ist das bei einem horizontalen Wurf, wo die Gewichtskraft immer senkrecht zum Erdboden gerichtet ist, obwohl die Bewegung ganz unterschiedlich gerichtet ist, immer längs der entstehenden Wurfparabel. Hier besteht die Funktion der Kraft darin, den geworfenen Körper von seiner geradlinigen Bewegung abzulenken, so dass er etwas in Richtung der Gewichtskraft beschleunigt wird, also nach unten.

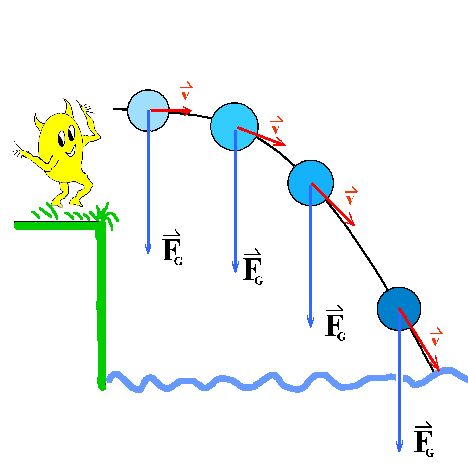Horizontaler Wurf eines Steins von einer Klippe ins Meer Die Bewegungsrichtung ist zu verschiedenen Zeitpunkten durch den Geschwindigkeitsvektor v eingetragen (rot). Abgesehen von der möglicherweise vernachlässigbaren Luftreibung wirkt nur mehr die Gewichtskraft FG (blau) als Kraft. Sie ist immer vertikal gerichtet. Sie sorgt dafür, dass der Geschwindigkeitsvektor v geändert wird. Die Kraft ist bei diesem Beispiel niemals in Bewegungsrichtung orientiert.

Bei ausgedehnten Körpern, an denen eine Kraft angreift, spielt für die Wirkung der Kraft auch noch der Angriffspunkt eine Rolle. Sie könnte dann z.B. den Körper drehen. Das beschreibt man üblicherweise durch eine andere physikalische Größe, das Drehmoment.

Wenn man ein Koordinatensystem einführt, kann man die Kraftrichtung leicht durch den Vergleich mit den positiven Koordinatenrichtungen angeben. Hat man ein Koordinatensystem gewählt, bei der die Kraft auf keinen Fall in y- und z-Richtung wirkt, kann sie nur in positive oder in negative x-Richtung wirken. In einem solchen Fall schreibt man z.B. F_x = - 10 N und meint damit eine Kraft, die ganz  in negative x-Richtung orientiert ist und den Betrag 10 N hat. Im allgemeinen Fall könnte man dann genauer z.B. F_x = -10 N, F_y = 5 N, F_z = 0 schreiben. Das wäre ein Kraftvektor F, die zum Teil in negative x-Richtung, aber auch zum Teil in positive y-Richtung orientiert ist. Bei eindimensionalen Bewegung mit nur einer Koordinatenachse lässt man den Index _x meistens weg und schreibt z.B. nur F = - 10 N  und meint auch da die Kraftkomponente in negative x-Richtung mit dem Betrag 10 N. Eine solche Vorgehensweise ist natürlich nur dann sinnvoll, wenn man sich vorher für ein bestimmtes Koordinatensystem entschieden hat.

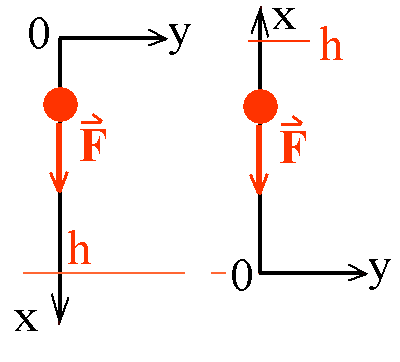Unterschiedliche Koordinatensysteme für denselben freien Fall aus einer Höhe h über dem Erdboden. Auf die fallende Kugel soll eine Gewichtskraft von 10 N wirken. links: Wahl des Koordinatenursprungs am Startpunkt, positive Koordinatenrichtung nach unten. Die Kraft F ist dann in positive x-Richtung orientiert, hat also die x-Koordinate Fx = 10 N. Dafür wird oft auch einfach F = 10 N geschrieben. Die Bewegung beginnt am Ort x = 0. Der Fall ist beendet, wenn der Ort x = h erreicht ist. Nach dem Start werden nur positive Orte durchlaufen. Der Ort (die Ortskoordinate) wächst, bis der Boden erreicht ist, alle Ortsänderungen sind positiv. rechts: Wahl des Koordinatenursprungs am Zielpunkt, positive Koordinatenrichtung nach oben. Die Kraft F ist dann in negative x-Richtung orientiert, hat also die x-Koordinate Fx = - 10 N. Dafür wird oft auch einfach F = - 10 N geschrieben. Die Bewegung beginnt am Ort x = h. Der Fall ist beendet, wenn der Ort x = 0 erreicht ist. Nach dem Start werden auch hier nur positive Orte durchlaufen, aber die Ortskoordinaten werden immer kleiner, bis schließlich der Boden erreicht ist: Alle Ortsänderungen sind negativ. Die Kugel bewegt sich entgegengesetzt zur positiven x-Richtung, also in negative x-Richtung.

Es ist in der Regel vollkommen egal, wie du das Koordinatensystem wählst. Es gibt auch keine Regel, dass - wie in der Mathematik meistens - die Koordinatenachse immer nach oben gerichtet sein muss. Es gibt auch noch weitere Möglichkeiten, zusätzlich zu den zwei erläuterten.

^*) Im Mathematik-Unterricht lernst du den Vektorbegriff wahrscheinlich in einer etwas anderen Weise kennen. Diesem Vektorbegriff und dem physikalischen liegen aber die gleichen Gesetze für die Multiplikation und Addition zugrunde, die gleichen "Vektorraum-Axiome". Deswegen - obwohl sie auf ersten Blick so unterschiedlich aussehen - handelt es sich bei beiden Begriffen um die gleiche Struktur von Vektoren.

Erst befinde sich ein Körper am Ort x_früher (z.B. 1 m), zu einer späteren Zeit t_später am Ort x_später (z.B. 5 m). Der Ort ändert sich also von x_früher (1 m) auf x_später (5 m), und zwar um die Ortsänderung x_später -  x_früher , im Beispiel also um 5 m - 1 m = 4 m. In diesem Fall ist die Ortsänderung positiv. Eine Ortsänderung ist positiv, wenn die Ortskoordinate im Lauf der Zeit wächst. Sie ist negativ, wenn die Ortskoordinate im Lauf der Zeit kleiner wird.

( zurück )