Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig-keiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Phys. Analysen Experi- ment des Monats Im- pres- sum Kommen-tare und Wünsche © Horst Hübel Würzburg 2005 - 2018

Temperatur und Entropie

Was ist Temperatur?

Hier geht es darum, was "Temperatur" bedeutet. Das hängt wiederum eng mit der Definition des Temperatur-Begriffes zusammen. Eine weitgehend davon unabhängige Frage ist, wie eine Temperatur-Skala definiert wird, und wie bestimmte Größen von der Temperatur abhängen.

Hier werden bekannte Fakten dazu zusammengetragen. Es ergibt sich daraus ein vereinfachender Vorschlag, wie Temperatur in der Schule definiert werden sollte.

Es gibt verschiedene miteinander verträgliche Temperatur-Definitionen:

• Die thermodynamische Temperatur-Definition
• Die Temperatur-Definition der Statistischen Mechanik

  Dem Buch " Wärme und Bewegung - die Welt zwischen Ordnung und Chaos, Heidelberg, Spektrum-der-Wiss.-Verlagsges., 1986, (Spektrum-Bibliothek, Bd. 8) von P.W. Atkins folgend wird für eines der einfachsten thermodynamischen Systeme (ein System, das nur zwei Energiestufen einnehmen kann) die Definition der Temperatur und der Entropie mit Hilfe von 2 Simulationsprogrammen erläutert. Sie stehen - für die Bildschirmauflösung 1024 x 768 - zum Herunterladen bereit.

  Mehr hierzu finden Sie in jedem beliebigen Lehrbuch der Statistischen Mechanik oder Thermodynamik.

Für die Schule ist zu überlegen, wie wesentliche Aspekte beider Definitionen in vereinfachter Weise berücksichtigt werden, so dass Schüler weder Fehlvorstellungen mitnehmen noch überfordert werden. Das wird diskutiert in

• Temperatur in der Schule

  Dort wird auch auf übliche schulische Missverständnisse eingegangen.

1. Die thermodynamische Temperatur-Definition

Zugrundegelegt wird ein Carnotscher Kreisprozess. Das ist eine idealisierte, ursprünglich auf einem idealen Gas als Arbeitsstoff beruhende Wärmekraftmaschine, die reversibel und periodisch zwischen zwei Wärmereservoirs mit unterschiedlichen Temperaturen arbeitet. Man nennt einen Prozess reversibel (umkehrbar), wenn er ständig Gleichgewichtszustände durchläuft. Es stellt sich heraus:

• Es gibt keinen Kreisprozess mit einem höheren Wirkungsgrad als dem der Carnot-Maschine.
• Ihr Wirkungsgrad η ist unabhängig vom verwendeten Arbeitsstoff.
• Für den Wirkungsgrad η gilt:  η = ( ΔQ₁ +ΔQ₂)/ΔQ₁ = (T₁-T₂)/T₁. Dabei ist ΔQ₁ die bei der höheren Temperatur T₁ aufgenommene Wärme, ΔQ₂ (<0) die bei der tieferen Temperatur T₂  "aufgenommene" (d.h. - ΔQ₂  > 0  ist die tatsächlich bei T₂ abgegebene Wärme).  (ΔQ₁ +ΔQ₂ ist die nach außen abgegebene Arbeit.)

Mit etwas Algebra ergibt sich                              ΔQ₁/T₁ = - ΔQ₂/T₂  bzw.    T₁/T₂ = - ΔQ₁/ΔQ₂ . *)

Temperaturen lassen sich also mittels einer idealen Carnot-Maschine vergleichen durch die Messung von Wärmemengen, also Energien. Nach Kelvin kommt man damit auch zu einer Temperaturskala, indem man einen Temperaturpunkt festlegt, z.B. den Tripelpunkt des Wassers mit T = 273,16 K. Diese Temperaturskala ist identisch mit der Temperaturskala aufgrund des idealen Gases.

Das ist eine konsistente Definition der Temperatur, da (nach Wikipedia "Thermodynamische_Temperatur"):

1. zwei reversibel und periodisch arbeitende Carnot-Maschinen zwischen den gleichen Reservoirs A und B genau den gleichen Wirkungsgrad haben, auch unabhängig vom verwendeten  Arbeitsstoff. D.h. bei gleichen Paaren von Reservoirs liefert jede beliebige reversibel und periodisch arbeitende Carnot-Maschine gemäß der Definition das gleiche Temperaturverhältnis. Andernfalls könnte man nämlich die Carnot-Maschine mit dem geringeren Wirkungsgrad "rückwärts" als Wärmepumpe betreiben, die Maschine mit dem höheren Wirkungsgrad vorwärts, und zwar so, dass dem Reservoir B gleich viel Wärme zugeführt wie entnommen wird. Dann hätte man insgesamt eine periodisch arbeitende Maschine, die nur dem Reservoir A Wärme entnimmt, daraus mechanische Arbeit gewinnt, jedoch Reservoir B unverändert lässt. Das wäre ein Perpetuum Mobile 2. Art, das nach dem zweiten Hauptsatz der Thermodynamik ausgeschlossen ist.

2. Betrachten wir drei Reservoirs A, B und C, jedes für sich im thermischen Gleichgewicht. Obige Definition liefert dann drei Temperaturquotienten T₁/T₂, T₂/T₃ und T₁/T₃. Damit die Temperaturdefinition widerspruchsfrei ist, muss eine Konsistenzbedingung gelten: Lassen wir eine erste Wärmekraftmaschine zwischen A und B und eine zweite Wärmekraftmaschine zwischen B und C operieren. Die erste Maschine entnehme dem Reservoir A eine Wärmemenge ΔQ₁ und führe dem Reservoir B die Abwärme ΔQ₂ zu. Die zweite Maschine entnehme dem Reservoir B genau die gleiche Wärmemenge ΔQ₂ und führe dem Reservoir C die Abwärme ΔQ₃ zu. Insgesamt wird also dem Reservoir B gleich viel Wärme zugeführt wie entnommen. Das System aus beiden Maschinen kann damit als eine Wärmekraftmaschine zwischen A und C aufgefasst werden. Aus den Gleichungen

ΔQ₁/ΔQ₂ = -T₁/T₂  und  (- ΔQ₂)/ΔQ₃ = -T₂/T₃   (die zweite Maschine nimmt - ΔQ₂ auf)

folgt ganz analog einerseits physikalisch und andererseits auch als Ergebnis einfacher Algebra die Konsistenzbedingung  ΔQ₁/ΔQ₃ = -T₁/T₃.

Danach muss man bzgl. der Temperatur-Definition sagen:

(D1a)   Nach der thermodynamischen Temperatur-Definition ist Temperatur T derjenige Parameter, der die Aufnahme und Abgabe von Wärme bei einer reversibel und periodisch arbeitenden Maschine mit dem höchstmöglichen Wirkungsgrad (also einer Carnot-Maschine) regelt. Reversibel heißt dabei: Die Aufnahme und Abgabe von Wärme erfolgt jeweils im thermischen Gleichgewicht.

Für die Schule vereinfacht, aber damit vereinbar ist: "T ist ein Parameter, der die Aufnahme und Abgabe von Wärme im thermischen Gleichgewicht regelt". Das ist vage kompatibel mit "Temperatur als Maß für den Wärmezustand". Bei zwei Systemen in Kontakt mit unterschiedlichem "Wärmezustand" fließt Energie vom wärmeren zum kälteren.

Nach *) wird die Entropie S definiert durch Entropieänderungen ΔS = ΔQ/T  . Dabei soll sich also bei der reversiblen Aufnahme der Wärmemenge ΔQ bei der Temperatur T eine Entropieänderung ΔS ergeben.  Bei einem reversiblen Prozess lässt sich dann jedem Zustand (p,V,T, ...) wegunabhängig eine Entropie S zuordnen (S ist eine Zustandsfunktion, die ein totales Differenzial besitzt): Ganz gleich, welche Zustände reversibel durchlaufen werden, gehört dann zu jedem Zustand (p,V,T, ...) eine eindeutige Entropie S. Für einem reversiblen Kreisprozess ist die gesamte Entropieänderung bei einem vollen Durchlauf 0, also ∫₀ dQ/T = 0 (mit einem Umlaufsintegral über einen geschlossenen Weg im p-V-Diagramm). (Aus dem Carnot-Prozess hatte sich ja ΔS₁ = ΔQ₁/T₁ = - ΔQ₂/T₂ = - ΔS₂ , also ΔS₁ + ΔS₂ = 0  ergeben.) Wenn S so definiert wird, wird bekanntes T vorausgesetzt, also z.B. definiert nach der thermodynamischen Temperatur-Definition. T ist aber umgekehrt auch T = ΔQ / ΔS   bzw. 1/T = ΔS / ΔQ. Man kann ahnen, dass damit Ableitungen zusammenhängen könnten. So muss jede andere, damit gleichwertige Definition die Beziehungen erfüllen:

mit partiellen Ableitungen. Die beiden Ausdrücke sind nicht einfach Kehrwerte voneinander, sondern unterscheiden sich durch die verwendeten grundlegenden Variablen (U und V  bzw.  S und V). Ähnlich sind auch die Innere Energie U und die (Helmholtzsche) Freie Energie F, häufig auch mit A abgekürzt, definiert durch F = U - T·S   Zustandsfunktionen, die ein totales Differenzial besitzen. Diese Definition wird später noch erläutert werden.

Zu 2. Die Temperatur-Definition der Statistischen Mechanik

Zum Download von 2 Simulationsprogrammen zur Untersuchung von Temperatur und Entropie, basierend auf Vorschlägen von P.W. Atkins. Sie sind für die Bildschirmauflösung 1024 x 768 vorgesehen.

Untersuchen Sie dazu mit Hilfe des PC-Programms ENTROPIE (nach P.W. Atkins) zwei Systeme A und B, die in thermischem Kontakt miteinander sind. A enthalte insgesamt Nmax_A Teilchen, B insgesamt Nmax_B Teilchen. Es soll sich um 2-Niveau-Systeme handeln, d.h. jedes Teilchen kann in einem von 2 Zuständen sein, im Grundzustand mit der Energie 0 und im angeregten Zustand mit der Energie E. N_A Teilchen sollen die Energie E haben, entsprechend N_B Teilchen.

Das könnte ein grobes Modell für ein Spin-System im äußeren Magnetfeld sein, wo die Spins entweder parallel (Energie E) oder entgegengesetzt zum Magnetfeld (Energie 0) ausgerichtet sind. Durch irgendwelche Prozesse, auf die es thermodynamisch nicht ankommt, kann ein Teilchen seine Anregungsenergie E verlieren und sie an irgendein anderes Teilchen in A oder B übertragen. Die Teilchen selbst sollen ortsfest sein. Es gibt also keine kinetische Energie in dem System. Insgesamt soll die (Gesamt-)Energie U (Innere Energie = Summe aller Teilchenenergien) konstant sein, sich aber über beide Systeme verteilen.

Gleichbedeutend damit wäre es, wenn ein angeregtes Teilchen aus dem Raum A in den Raum B übertritt und stattdessen ein Teilchen im Grundzustand von B nach A, wenn mit diesen Platzwechselvorgängen keine Energieänderung (sondern nur ein Energietransport) verbunden ist.

Das Programm lässt zwei Analysemöglichkeiten zu:

• Eine "experimentelle Analyse", bei der das Verhalten beider Teilsysteme simuliert wird.
• Eine "theoretische Analyse", bei der für alle möglichen Verteilungen der angeregten Teilchen Kenngrößen wie Temperatur, Entropie oder innere Energie berechnet  und dargestellt werden, ganz gleich wie die untersuchte Verteilung zustande kommt.

2.1. Experimentelle Analyse der Fluktuationen:

2.1.1 In einer Versuchs-Variante 1 sollen anfangs N_A Teilchen in A angeregt sein, keines in B.

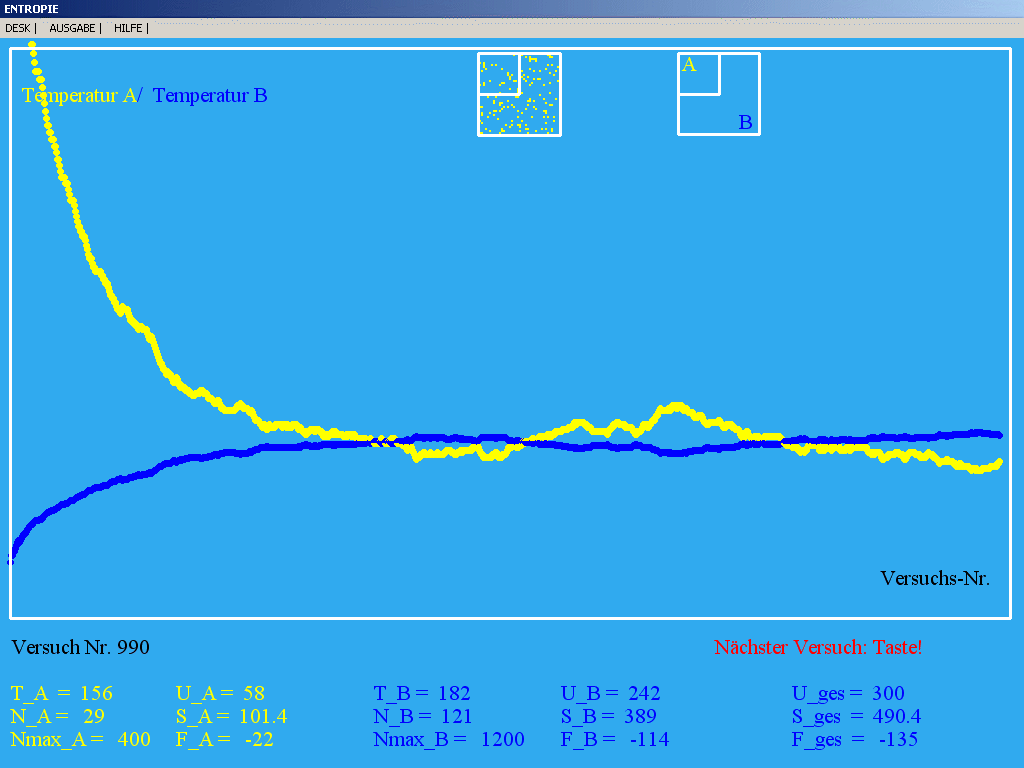Abb. 1: Experimentelle Analyse (Simulation) des Zwei-Niveau-Systems in Räumen A und B im thermischen Kontakt (Nmax_A = 400; Startwert N_A = 150; Nmax_B = 1200; Startwert N_B = 0 ). Es werden jeweils Versuche durchgeführt, bei denen die Energie von zufällig ausgewählten Teilchen verändert wird, bis wieder insgesamt N_A + N_B = 150 Teilchen im höherenergetischen Zustand sind. Man erkennt die Fluktuationen der Temperaturen beider Teilsysteme, das Streben gegen einen gemeinsamen ("dynamischen") Grenzwert, und das Entropie-Maximum (hier als dynamischer Grenzwert der Entropie S mit zunehmender Zahl von Versuchen) mit dem Wert 490,4 in willkürlichen Einheiten, berechnet nach einer später zu besprechenden Methode. Weil hier immer N_A < Nmax_A/2,  ist die Temperatur stets positiv (keine Besetzungszahl-Inversion).

In einem "Versuch" soll jetzt eine neue Verteilung der konstanten Energie über die Zustände von A und B erfolgen. Die sich einstellenden Zahlen der angeregten Teilchen in A und B (N_A und N_B) werden registriert. Nach vielen Versuchen zeigt sich, dass sich Mittelwerte von N_A und N_B herausbilden, um die die Teilchenzahlen schwanken, stärker beim kleineren System A. Abgesehen von diesen Fluktuationen stellt sich also nach und nach ein weitgehend stabiler Wert für die Verhältnisse N_A/Nmax_A und N_B/Nmax_B ein. Beide Wert sind nach Einstellung des "thermischen Gleichgewichts" gleich (das muss eine Bedeutung haben!). Die Fluktuationen von Versuch zu Versuch werden im Quadrat oben mitte auch visuell dargestellt, indem die angeregten Teilchen gelb markiert werden.

2.2.  Experimentelle Analyse: Was kann man über die Energieströmung zwischen zwei Systemen in thermischem Kontakt aussagen?

Die gesamte Energie eines Systems oder Teilsystems, die nicht makroskopischer Art ist, heißt Innere Energie U. Auch nach Einstellung des thermischen Gleichgewichts fluktuieren die Inneren Energie U_A und U_B in beiden Systemen, obwohl insgesamt die Summe konstant ist. Die dabei von einem System ans andere übertragene Energie heißt Wärme Q. Wärme fließt dann einmal von A nach B, ein andermal von B nach A. Im zeitlichen Mittel ist die Innere Energie nach Erreichen des thermischen Gleichgewichts aber in beiden Teilsystemen konstant. Der für die Wärmelehre wesentliche Anteil der Inneren Energie steckt in solchen fluktuierenden Anregungen. Nur er wird hier betrachtet. Zu den Anregungszuständen könnte auch, bei einem Gas etwa, die "ungeordnete Teilchenbewegung" gehören.

Die Einstellung des thermischen Gleichgewichts ist mit einem überwiegenden Energiefluss von A nach B verbunden, wenn anfangs in A prozentual mehr angeregte Teilchen vorhanden waren als in B. ( N_max  - N )/N ist das Verhältnis der Teilchenzahlen von nicht angeregten und angeregten Teilchen eines Teilsystems. Wenn versuchsweise T's als Funktionen der Teilchenzahlverhältnisse  ( N_max  - N )/N definiert werden:

dann könnte anfangs T negativ sein, wenn nämlich mehr als 50% der Teilchen angeregt sind, wenn also N >= 1/2 N_max. Das soll jetzt nicht betrachtet werden. Ihm entspricht auch eine Situation, die sich nur künstlich erreichen lässt (so genannte "Besetzungszahl-Inversion"). Der Faktor E/k_B sorgt dafür, dass k_BT die Dimension einer Energie hat. E dabei hat wesentliche Bedeutung für die Interpretation von diesem T.

Ohne Besetzungszahl-Inversion ist mit dem anfänglichen N_B = 0  T₂ = 0 und T₁ > T₂. Das bleibt auch so bis zur Einstellung des thermischen Gleichgewichts. Dann gilt offenbar bis auf Abweichungen durch Fluktuationen:   T₁ = T₂.

Folgerungen:

• (Im Mittel) findet ein Energiefluss von A nach B dann statt, solange   T₁ > T₂.  Sie erkennen das daran, dass U_A dann abnimmt, während U_B zunimmt. Das entspricht der Erfahrungstatsache, dass Wärme (ohne äußere Arbeit) immer vom wärmeren System zum kälteren fließt. Das passt zu einer Deutung von T₁ und T₂ als Temperatur.

  Temperatur T ist also derjenige Parameter, der den Energiefluss zwischen zwei Systemen im thermischen Kontakt miteinander regelt. Das ist verwandt mit der Definition (D1a).

Jetzt folgt ein neuer Gedanke:

• Der absolute Temperaturnullpunkt (z.B. T₂ = 0) ist dadurch gekennzeichnet, dass kein Teilchen angeregt ist (das die höhere Energie E besitzt), dass alle Teilchen im Grundzustand sind.

• Je höher T ist, desto höher ist der Bruchteil der Teilchen, die im jeweiligen Teilsystem angeregt sind (die die höhere (Anregungs-)Energie E haben). Für ihn gilt nach kurzer Rechnung wegen:

  E / k_BT   = log(  ( N_max  - N )/N  )  

  ( N_max  - N )/N  = exp ( E / k_BT )  

  N_max  /N    - 1 =  exp ( E / k_BT  )    

  N_max  /N    =  1 + exp ( E / k_BT  )

  also

                 

  N / Nmax  =   1/  ( 1 +  exp ( + E / kBT ) )  = exp ( - E / kBT ) /  ( 1 +  exp ( - E / kBT ) )

  Die Funktion f(x) = exp(-x)/(1+exp(-x)) = (1+exp(x))^-1  ist eine monoton fallende Funktion. Für x => 0 (T =>∞ ¥   einem festen E >0) strebt f(x) => 1/2: ca. gleich viele Teilchen sind dann im angeregten wie im Grundzustand. Für x => &in  ( T => 0) verhält sich f(x) wie exp(-x) und geht gegen 0: immer weniger Teilchen sind im angeregten Zustand.

• Die mittlere Energie eines Teilchens ist <E> = (  (N_max - N)·0 + N·E ) / N_max = N/N_max ·E =  E exp ( - E / k_BT ) / ( 1 +  exp ( - E / k_BT ) ) . Sie strebt gegen 0 für T => 0 und gegen E/2 für T => ∞. (Inwiefern ist also <E> ein Maß für die Temperatur?) Im Nenner steht die so genannte Zustandssumme Z aus "Boltzmann-Faktoren" exp( - E_i / k_BT ) mit der Summe über alle möglichen Energiestufen E_i :

  Z = ∑i exp ( - Ei / kBT )   .

• In allgemeineren Fällen kann man die mittlere Energie <E> mit den Wahrscheinlichkeiten p(E_i) = exp ( - E_i / k_BT ) / Z für die Besetzung eines Energieniveaus mit der Energie E_i berechnen:   

  <E> = ∑i  p(Ei )·Ei   .

  In Exponenten von p(E_i) = exp ( - E_i / k_BT ) / Z werden sozusagen jeweils zwei Energien miteinander verglichen: Die Anregungsenergie E_i und k_BT. Je größer k_BT im Vergleich zu E_i ist, desto größer ist die Wahrscheinlichkeit, dass Teilchen in das Niveau mit der Energie E_i angeregt sind, grob: desto mehr Teilchen haben die erhöhte Energie E_i (E_i sind die Anregungsenergien gegenüber dem Grundzustand; vgl. Anhang 2). Hier also bewährt sich der Ansatz für T; formal müssen natürlich auch die Argumente der Exponentialfunktionen dimensionslos sein.

All dies passt recht gut zur Deutung von T₁ und T₂ als Temperaturen.

Damit könnten wir sagen:

(D1b)  Die Temperatur T eines Systems ist ein Parameter, der im thermischen Gleichgewicht bestimmt, wie die Energie über die Energieniveaus der Mikrozustände (E₁, E₂, E₃, ... ) verteilt ist.

Für die Simulation des Programms wird vorausgesetzt, dass die beiden Teilsysteme jeweils für sich im thermischen Gleichgewicht sind. Nur so hat es einen Sinn, eine Temperatur zu definieren.

2.3. Experimentelle Analyse: Wodurch ist das thermische Gleichgewicht bestimmt?

2.3.1 Dazu zuerst etwas Theorie: Die Teilchenzahl-Verhältnisse N_A/Nmax_A und N_B/Nmax_B nähern sich offenbar mit zunehmender Zahl von Versuchen bis auf Fluktuationen einem gemeinsamen Grenzwert ("dynamischer Grenzwert"). Durch diese Gleichheit ist das thermische Gleichgewicht bestimmt. Damit verbunden ist eine gemeinsame Temperatur T.

Offenbar gibt es i.A. für ein bestimmtes Teilchenzahl-Verhältnis sehr viele Verteilungen der angeregten Teilchen über beide Teilsysteme. Im Extremfall, wenn N_A = Nmax_A und N_B = 0 gibt es dagegen genau eine Verteilung. Der Übergang von diesem Zustand zum thermischen Gleichgewicht ist offenbar mit einer gewaltigen Vermehrung der möglichen Verteilungen verbunden. Wenn umgekehrt N_A = 0  gibt es für das System im Raum A ebenfalls genau eine Verteilung. Kann man diesen Übergang zum Maximum genauer untersuchen? Dazu werden mit dem natürlichen Logarithmus log zwei Funktionen S₁ und S₂ definiert:

ist dabei die Anzahl der möglichen Verteilungen von N angeregten Teilchen aus insgesamt N_max Teilchen, wobei also N_max - N Teilchen im Grundzustand sind.

Das mathematische Symbol für "N aus N_max" ist mit dem Ergebnis identisch.

Jede dieser g(N_max,N) Einstellmöglichkeiten wird ein "Mikrozustand" genannt, der zu dem "Makrozustand" (N_max,N ) beitragen kann.

Der Ausdruck für g((N_max,N) ist leicht verständlich: Um insgesamt N_max Teilchen zu verteilen, gibt es N_max! Möglichkeiten. Dabei sind aber diejenigen äquivalent, bei denen nur die angeregten Teilchen N untereinander und die nicht angeregten Teilchen untereinander vertauscht werden. Deshalb muss durch die beiden Fakultäten im Nenner dividiert werden.

Bei der Simulation wird durch g(N_max,N) berechnet, auf wie viele Weisen sich bei jedem Versuch das resultierende Wertepaar (N_max,N ) einstellen kann.

Es stellt sich heraus, dass die Funktionen S₁  und S₂ wachsen und fallen, aber dass S₁ + S₂ einem Maximalwert zustrebt, wenn sich die beiden Systeme dem thermischen Gleichgewicht nähern. Höchstens durch kurzzeitige Fluktuationen wird dieser Maximalwert überschritten und wieder unterschritten, wenn er einmal erreicht ist. Wechseln nämlich immer mehr Anregungen (nicht Teilchen) von Teilsystem A in Teilsystem B, so vermehren sich zunächst die Verteilungsmöglichkeiten in A und auch in B. Sind aber quasi alle Anregungen aus A in B übergewechselt, gibt es in A wie in B immer weniger Verteilungsmöglichkeiten (wir wissen: in A dann genau eine). Dazwischen gibt es Bereiche, bei denen die Zahl der Verteilungsmöglichkeiten in A und B unterschiedliche Tendenz haben. Zwischen den geschilderten Extrema gibt es also eine Aufteilung, bei der die Zahl der erreichbaren Verteilungsmöglichkeiten, charakterisiert durch S₁ + S₂, maximal wird. Das geschieht beim thermischen Gleichgewicht. S₁ + S₂ hat also eine physikalische Bedeutung und wird Entropie genannt. Ebenso sind S₁ und S₂ Entropien der Teilsysteme. Allgemein:

S(Nmax,N) = kB   log g(Nmax,N)   , wobei g die Anzahl der möglichen Mikrozustände ist, die zu einem Makrozustand (Nmax,N) beitragen können.

Das thermische Gleichgewicht stellt sich ein, weil wegen des Maximums der Zahl der möglichen Verteilungen (des Maximums der Entropie) "maximal viele Wege dorthin führen". Das thermische Gleichgewicht ist durch die wahrscheinlichste Aufteilung der angeregten Teilchen in Bereich A und B gekennzeichnet.

Die Entropie S ist ein Maß für die Zahl der möglichen Verteilungen.

2.3.2 In der Versuchs-Variante 2 mit anfänglichem N_A = 0 des Versuchs beobachten Sie die Fluktuationen der Temperaturen und Teilchenzahl-Verhältnisse in beiden Systemen nahe dem thermischen Gleichgewicht (beim Entropie-Maximum). Die Fluktuationen sind beträchtlich, aber geringer im größeren System. Man kann erwarten, dass sie in sehr großen Systemen (N_max in der Größenordnung der Avogadrokonstanten) nicht mehr auffallen.

2. 4. In einer theoretischen Analyse wird nicht mehr die Einstellung des thermischen Gleichgewichts simuliert, sondern es werden für alle möglichen vorgegebenen Verteilungen der angeregten Teilchen (wie auch immer diese zustandekommen) die thermodynamischen Funktionen S, T, U und F  mit den oben besprochenen Definitionsformeln berechnet und dargestellt. Dabei kommen in realen physikalischen Systemen negative Temperaturen i.A. nicht vor (nur erreichbar bei "Besetzungszahl-Inversion"; rot markiert). Auch abnehmende Werte der Gesamt-Entropie werden so gut wie nie beobachtet (rot markiert). Sie erkennen:

• Die Entropie wird maximal gerade bei der wahrscheinlichsten Verteilung (auch akustisch markiert durch Gong). Es gibt dann maximale Anzahl von Möglichkeiten, die Aufteilung zu realisieren.
• Für die wahrscheinlichste Aufteilung sind die Temperaturen beider Systeme wieder gleich.
• Die bei den gleichen Daten ermittelte Entropie des Maximums stimmt mit der Gleichgewichts-Entropie der "experimentellen Analyse" überein, die sich als "dynamischer Grenzwert" bei vielen Versuchen einstellt.
• Die Fluktuationen fallen prozentual umso weniger ins Gewicht, je größer das System ist. Sehr große Systeme im thermischen Gleichgewicht haben quasi konstantes Verhältnis der Zahl angeregter Teilchen zur Gesamtzahl, quasi konstante Temperatur und quasi konstante Entropie. Als Folgerung ergibt sich auch eine quasi konstante mittlere Energie <E> eines Teilchens.

Das thermische Gleichgewicht entspricht also der wahrscheinlichsten Aufteilung der Energie über beide Systeme bzw. dem Maximum der Gesamt-Entropie.

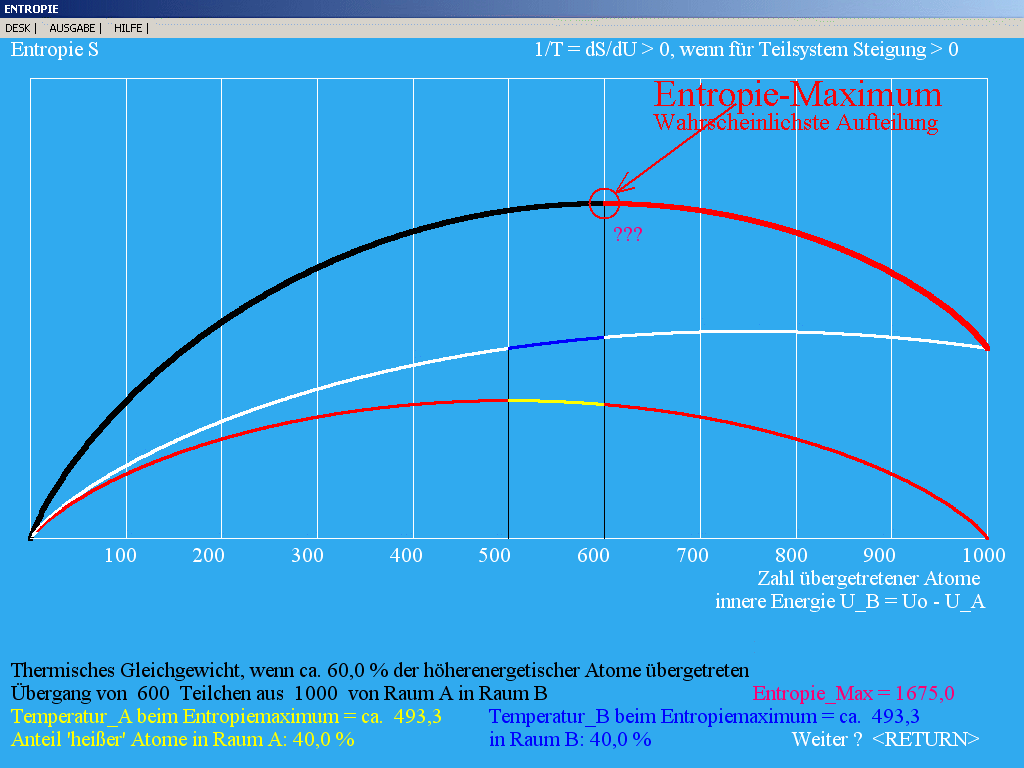Abb. 2: Theoretische Analyse des Zwei-Niveau-Systems in Räumen A und B im thermischen Kontakt (N_A = Nmax_A = 1000; Nmax_B = 1500 ) Die Entropiekurve 1 (unterste Kurve) von N_A = 0 bis N_A = 500 ist rot gezeichnet, weil hier N_A >= Nmax_A (negative Temperatur). Von N_A = 600 bis 1000 ist auch die Gesamt-Entropie  (oberste Kurve) rot markiert, weil diese in diesem Bereich entgegen den Beobachtungen abnehmen müsste. Mit den Daten von Abb. 1 würde sich der dort experimentell ermittelte Gleichgewichtswert von S als maximale Gesamt-Entropie hier bei ca. 121 übergetretenen Teilchen ergeben.

Im Graphen sind die Entropien incl. der Gesamt-Entropie an Abhängigkeit von N_B (bzw. der aus A übergetretenen Teilchen) dargestellt. Es bestätigt sich:

• Beim thermischen Gleichgewicht ist die Entropie maximal.
• Beim thermischen Gleichgewicht sind die Temperaturen beider Teilsysteme gleich.
• Beim thermischen Gleichgewicht haben beide Teilsysteme das gleiche Verhältnis der Teilchenzahlen von angeregten und nicht angeregten Teilchen.

Beachten Sie: All dies ist nur eine Folge der Statistik, also des geschickten Zählens bzw. des "Gesetzes der großen Zahlen", nicht von irgendwelchen "Mechanismen", die ein bestimmtes Verhalten der Teilchen "bewirken" würden. Der Gleichgewichtszustand ist der Zustand, zu dem die meisten Wege führen, der sich auf maximale Anzahl von Weisen realisieren lässt. Über die Teilchen selbst wurden fast keine Annahmen gemacht, außer dass sie in einem Grundzustand mit der Energie 0 und einem angeregten Zustand mit der Energie E vorkommen können.

Die Steigung im Graphen ist proportional zur Ableitung von S_A nach N_B (bzw. Nmax_A - N_A) und zur negativen Ableitung ∂S_A/∂U_A bzw. zur Ableitung von S_B nach N_B und  zur Ableitung ∂S_B/∂U_B. Beide Ableitungen nach der Teilchenzahl sind beim Entropiemaximum entgegengesetzt gleich; ihre Summe ist 0. Damit ist plausibel gemacht, dass das thermische Gleichgewicht mit einem Extremum der Gesamt-Entropie verbunden ist. Die Temperatur wird wie oben definiert und für jede mögliche Verteilung berechnet, unter der Annahme, dass sich jedes Teilsystem für sich im thermischen Gleichgewicht befindet. Im thermischen Gleichgewicht, wenn also die Gesamt-Entropie maximal ist, sind die Temperaturen beider Teilsysteme gleich, wie auch die Ableitungen ∂S_A/∂U_A und ∂S_B/∂U_B.

Allgemein wird definiert:    1/T = (∂S(U,V)/∂U)_{V= konst} oder auch 1/T = (∂S(U,V)/∂U)_{Nmax = konst}.   Darin ist die im Programm verwendete speziellere Definition für sehr große Teilchenzahlen enthalten (Anhang). Also:

(D2a)  Die Temperatur T misst, wie sich die Anzahl der erreichbaren Zustände (in S enthalten) bei einer bestimmten Änderung der Inneren Energie U verändert.

oder auch  gemäß             T = (∂U(S,V)/∂S)_{V= konst}.

(D2b)  Die Temperatur T misst, wie sich die Innere Energie U bei einer bestimmten Änderung der Anzahl der erreichbaren Zustände (in S enthalten) verändert.

Auch die Freie Energie F = U - T·S nimmt im thermischen Gleichgewicht einen konstanten Wert an.

Unabhängig davon, was der Begriff  "Temperatur" bedeutet, ist die Frage, wie eine Temperatur-Skala definiert wird. U.a. sind folgende Definitionen der Temperaturskala in Gebrauch:

• die eben beschriebene thermodynamische Temperatur-Skala,
• die auf den Gesetzen des idealen Gases beruhende Skala, beruhend auf p·V = N·k_B·T   bzw. p·V = n·R·T  (mit Druck p, Volumen V, Teilchenzahl N, Stoffmenge n (Anzahl der Mole des idealen Gases), Boltzmannkonstante k_{B ,}  allgemeiner Gaskonstanten R und (absoluter) Temperatur T. Bei konstanten Druck gilt dann    T₁/T₂ = V₁/V₂  und man kann Temperaturen vergleichen über Volumenmessungen von realen Gasen (z.B. He), die sich über weite Strecken wie ein ideales Gas verhalten.

3. Temperatur in der Schule:

Es sind verschiedene Definitionen der Temperatur in der Schule in Gebrauch (SD..: schulische Definition):

(SD1) Temperatur ist, was das Thermometer misst.

Darauf läuft es hinaus, wenn die Wärmelehre mit der Besprechung von Thermometern begonnen wird. Das ist eine praktikable, aber auch für die Schule etwas unbefriedigende Definition. Insbesondere ist für die Schüler kein Anlass erkennbar, die Anzeige nicht - wie in der Umgangssprache - "Wärme" zu nennen.

(SD2) Temperatur ist ein objektives Maß für den "Wärmezustand" eines Systems.

Das ist der traditionelle Weg. "Wärmezustand" (Betonung auf Zustand; eigentlich müsste es "thermischer Zustand" heißen) kann in der Schule wohl nicht exakt definiert werden. Das ist aber auch verzichtbar. "Wärmezustand" sollte aber in Zusammenhang gesetzt werden mit:

• "heiß - kalt"
• Je höher die Temperatur, desto mehr Teilchen sind in höhere Energiezustände angeregt. (Bei Gas, Flüssigkeit, Kristall: desto mehr Teilchen haben eine höhere kinetische Energie in der ungeordneten Bewegung.)
• Je tiefer die Temperatur, desto weniger Teilchen haben eine höhere Energie als die Grundzustandsenergie.

  Wie gesagt: Dabei ist immer von der Gesamtenergie E der Teilchen die Rede, die - je nach System - Photonenenergie (Hohlraumstrahlung), kinetische Energie (ideales Gas), kinetische und potenzielle Energie (reales Gas, Molekülgase), magnetische Energie (Spinsystem) etc. sein kann.

• Je höher die Temperatur im Vergleich zu der eines zweiten Körpers in thermischem Kontakt, desto mehr Energie fließt bei sonst gleichen Bedingungen (also z.B. in gleicher Zeit) vom heißen zum kalten Körper.

Die folgenden Aspekte überfordern wohl die Schüler, wenn nicht Entropie als Begriff explizit behandelt wird (man beachte: Entropie ist ein Maß für die Zahl der erreichbaren Zustände):

• Je höher die Temperatur, desto weniger Entropieänderung ΔS tritt ein bei derselben Wärmezufuhr ΔQ
• Je höher Temperatur, desto größere Wärmezufuhr ΔQ ist zur gleichen Entropieänderung ΔS nötig.

Es genügt  m.E. für die Schule, die ersten vier Punkte in den Raum zu stellen. Insbesondere erscheint auch der Hinweis sehr nützlich, dass bei höherer Temperatur mehr Teilchen eines Systems in höhere Energiezustände (der Gesamtenergie) angeregt sein können.

Dabei ist es offenbar gleichgültig, um welche Energie es sich handelt. Das könnte kinetische Energie sein wie bei einem idealen Gas, das ja keine andere Energie haben kann. Das könnte die Summe aus kinetischer und potentieller Energie sein wie bei einem realen einatomigen Gas oder bei Molekülschwingungen eines zweiatomigen Gases, deren Mittelwerte bei harmonischen Kräften gerade gleich groß sind und damit in gleicher Weise von der Temperatur abhängen. Das könnte magnetische Energie sein wie im einfachen System des Programms ENTROPIE, wo es keine kinetische Energie und keine Teilchenbewegung gibt.

(SD3) Temperatur ist ein Parameter, der die Aufnahme und Abgabe von Wärme im thermischen Gleichgewicht bei Kontakt zwischen zwei Systemen regelt. Dies entspricht der thermodynamischen Definition der Temperatur (D1a). Das Argument kann die Vorstellung von Temperatur unterstützen; bleibt aber recht abstrakt.

(SD4) Die Temperatur T ist ein Parameter, der bestimmt, wie die Energien von Teilchen im thermischen Gleichgewicht verteilt sind. Je höher die Temperatur T, desto mehr Teilchen werden in höhere Energien angeregt, oder in desto höhere Energien werden Teilchen angeregt, "desto mehr Teilchen haben eine höhere Energie".

Diese Definition präzisiert (SD2) und entspricht im Wesentlichen (D1b).

Etwas vager: "Temperatur T ist ein Maß dafür, "welche (mikroskopischen) Energien im thermischen Gleichgewicht besetzt werden können."

Ich würde an der Schule die Definition (SD2) bevorzugen und sie später durch (SD4) ergänzen.

Warnungen:

1. Nicht als Temperatur-Definition verwendet werden sollte: "Temperatur wird definiert als Maß für die mittlere kinetische Energie eines Teilchens", obwohl die Vorstellung sehr nützlich ist, dass bei höherer Temperatur Teilchen in schnellerer ungeordneter Bewegung sind. Das entspricht ja den Definitionen (D1b) und (SD4). Die Behauptung mit dem starken Bezug auf die kinetische Energie ist überflüssig, da es nur geringfügig schwieriger ist, gemäß (SD4) allgemeine Energien bei den angeregten Zuständen ins Spiel zu bringen, wie es die Thermodynamik verlangt.

Statt zu sagen

"T ist ein Maß für mittlere kinetische Energie eines Teilchens im thermischen Gleichgewicht. Je höher die Temperatur, desto höher ist die mittlere kinetische Energie" (Aussagen, die für ein ideales Gas als Aussage über die mittlere kinetische Energie eines Teilchens halbwegs richtig sind),

kann man, nur geringfügig weniger griffig (dafür aber verallgemeinerungsfähig und nicht ein Verständnis blockierend), die Definition (SD4) verwenden.

Es gibt noch eine sprachliche Schwierigkeit bei der häufig in Schulbüchern verwendeten Definition ("Temperatur als Maß für die mittlere kinetische Energie der Teilchen"): Das klingt so, als sollte die kinetische Energie aller Teilchen eines Systems betrachtet werden (also ihre Summe) und davon sollte dann ein Mittelwert genommen werden. Genau genommen ist dann nicht der Unterschied zur inneren Energie (als Summe der Energien aller Teilchen) erkennbar, weil der Mittelwert nur eines Wertes mit dem Wert übereinstimmt. Tatsächlich nimmt man den Mittelwert der Energien jedes einzelnen der Teilchen, wie es eine Definition im Sinne von "Temperatur als Maß für die mittlere Energie eines Teilchens des Systems" verlangt.

2. Nicht hilfreich ist es, wenn man Innere Energie U und Temperatur T gegeneinander abgrenzen möchte, sich auf eine Unterscheidung von Innerer (Gesamt-)Energie U und mittlerer (kinetischer oder Gesamt-) Energie <E> als Maß für T zu beschränken, da ja gilt: U = <E>·N (evtl. bis auf thermisch irrelevante Anteile; i.A. <E> mittlere Gesamtenergie eines Teilchens des Systems),  wenn die Teilchenzahl N konstant ist, wie das in den schulischen Beispielen häufig der Fall ist. Bei fester Teilchenzahl N sind U und <E> proportional zueinander und hängen, auch beim idealen einatomigen Gas,  in der gleichen Weise von T ab. Wenn es nur ideale Gase gäbe, wären beide ein Maß für die mittlere Energie eines Teilchens, U auch noch für die Teilchenzahl. Es ist dann kaum einzusehen, dass man zwei verschiedene Begriffe U und T für "das fast Gleiche" benötigt.

Die Wesensverschiedenheit beider Begriffe bemerkt man erst, wenn man Systeme mit unterschiedlichen Teilchenzahlen, aber gleicher Temperatur oder aber gleicher Innerer Energie, vergleicht. Dann wird auch evident, dass U eine extensive Größe ist, die von der Teilchenzahl abhängt, T aber eine intensive, die unabhängig von der Teilchenzahl ist. Mit dieser wesentlichen Aussage verträglich ist es, dass U die gesamte Energie (egal ob kinetische oder potenzielle oder gar eine ganz andere) des Systems misst, und T ein Parameter ist, der den "Wärmezustand" jedes beliebigen Teils des Systems misst, wenn dieser mit dem Rest im thermischen Gleichgewicht ist. Mit zwei "Modellgasen" mit 3 bzw. 5 Teilchen gleicher mittlerer Energie habe ich das durch einfache Kopfrechnungen meinen Schülern klar gemacht. Man verwende dazu einfache, wenn auch unrealistische Zahlenwerte (z.B. "Gas 1"  mit 3 Atomen von 1 J, 3 J und 5 J, "Gas 2" mit 5 Atomen von 1 J, 2 J, 3 J, 4 J und 5 J, jeweils der Gesamtenergie).

3. Die Betonung des Wortteils "kinetischer" Energie im Unterschied zu (mittlerer) potenzieller Energie ist zudem verfehlt, da ein ideales einatomiges Gas ja nur kinetische Energie besitzt. Von einer Betrachtung des idealen Gases her kann man überhaupt keine Aussage machen, wie sich eine mittlere potenzielle Energie verhalten würde. Darüber macht in anderen Fällen der "Virialsatz" Aussagen. Wie auch die Überlegungen zum Programm ENTROPIE zeigen, geht es in der Statistischen Mechanik um die Gesamtenergie E der Einteilchen-Zustände.

4. Vielfach wird aus einem missverstanden Verhalten der mittleren kinetischen Energie fälschlich auf das Verhalten der Temperatur geschlossen. Dabei wird nicht beachtet,

• dass dort, wo ein System kinetische und potenzielle Energie besitzt, beide im thermischen Mittel häufig gleiche Temperaturabhängigkeit aufweisen,
• dass in die Quantentheorie (die ja eigentlich der Statistischen Mechanik zugrundeliegt) ohnehin nur Eigenzustände der Gesamtenergie eingehen,
• dass bei harmonischen Kräften die Mittelwerte von E_kin und E_pot sogar exakt gleich sind (wie der Virialsatz behauptet) und damit mit Sicherheit die gleiche Temperaturabhängigkeit besitzen.

5. Vielfach wird auch fälschlich die Konstanz der Temperatur beim Sieden oder Schmelzen dadurch erklärt, dass während des Schmelzens oder Siedens durch Energiezufuhr nur die mittlere potenzielle Energie gesteigert werde, die mittlere kinetische Energie hingegen konstant bleibe. Wie Sie wissen, kann man in dynamischen Systemen potenzielle Energie nur steigern (bis zur Ablösung eines Teilchens), indem man gleichzeitig die kinetische Energie erhöht! Wesentlich ist, dass bei solchen Phasenübergängen die schnellsten Teilchen (mit der höchsten Energie) aus der einen Phase (Teilsystem A) in die andere (Teilsystem B) abwandern. Die um die Bindungsenergie geänderte (konstante) Grundzustandsenergie für die zweite Phase hat keinen Einfluss auf die Besetzungszahl-Verhältnisse bzw. die mittlere Energie eines Teilchens der Phase A. Beide Teilsysteme müssen auch gleiche Temperatur haben, weil sie in thermischem Kontakt miteinander stehen.

6. Zudem gibt es viele wichtige Systeme, die gar keine kinetische Energie, aber doch eine Temperatur besitzen, wie zum Beispiel die Hohlraumstrahlung oder die kosmische Hintergrundstrahlung oder ein Spinsystem. Würde man die Temperatur "als Maß für die mittlere kinetische Energie eines Teilchens" definieren, wäre unverständlich, dass Strahlung eine Temperatur haben kann. So wird üblicherweise das Stefan-Boltzmann-Gesetz aus der Inneren Energie eines Photonengases und seiner Temperatur hergeleitet. Früher, bevor man erkannte, dass Strahlung ein eigenes thermodynamisches System mit einer eigenen Temperatur sein kann, behalf man sich mit der Hilfsvorstellung, dass die im Strahlungsgesetz vorkommende Temperatur die Temperatur der Hohlraumwände sei, die ja im Idealfall wirklich mit der Strahlung im thermischen Gleichgewicht stehen und also die gleiche Temperatur wie diese haben.

7. Zur Frage, welche Temperatur ein Vakuum hat, lautet die Standard-Antwort, dass es keine habe, da es keine Materie enthalte, die mit einer kinetischen Energie verbunden sei. Selbstverständlich ist, dass ein "System" vorhanden sein muss, dessen thermisches Verhalten man durch eine Temperatur beschreiben könnte. Gäbe es ein absolutes Vakuum, so würde dieses System fehlen. Gäbe es aber einen absolut materiefreien Raum, so enthielte dieser durchaus noch Strahlung. Wenn diese im thermischen Gleichgewicht ist, besitzt sie eine Temperatur. So ist der intergalaktische Raum - das beste existierende "Vakuum" - weder ganz materiefrei (typisch 1 Atom pro cm³) noch frei von der kosmischen Hintergrundstrahlung, die sehr wohl eine Temperatur hat.

Mit dem Programm ENTROPIE wird stattdessen die übliche korrektere und allgemeinere Auffassung von T veranschaulicht.

Die Lehrplanformulierung "absolute Temperatur als Maß für die mittlere kinetische Energie eines Teilchens" ist korrekt zu lesen als: "Die mittlere kinetische Energie eines Teilchens ist proportional zur absoluten Temperatur". Sie macht eine Aussage über die mittlere kinetische Energie eines Teilchens. Sie wird falsch interpretiert, wenn sie als Definition oder Begriffserklärung der absoluten Temperatur aufgefasst wird.

**) Korrekt müsste der Satz umgekehrt werden: "Die mittlere (kinetische) Energie eines Teilchens (wie auch die innere Energie U des Gases) im thermischen Gleichgewicht ist proportional zu T. Je höher die Temperatur, desto höher ist die mittlere (kinetische)  Energie". Der Satz macht eine Aussage über die mittlere (kinetische) Energie und nicht über die Temperatur. Wenn es nur ideale Gase gäbe, könnte man darauf eine Temperaturdefinition aufbauen bzw. ihn, wie oben zitiert, als Aussage über die Temperatur lesen. Aber auch an der Schule spielen andere Systeme (reale Gase, Strahlung) eine wichtige Rolle. In jedem Fall aber erlaubt der zugrunde liegende Sachverhalt die Definition einer Temperatur-Skala, die in weiten Grenzen praktisch durchführbar ist, weil es Gase gibt, die sich weitgehend wie ein ideales Gas verhalten.

II Entropie

Mit dem Programm 2KAMMGAS ("Zweikammer-Gas") wird die (reversible) Diffusion eines Gases aus einem Volumen A durch eine Öffnung in ein Volumen B untersucht. Die Meinung ist die, dass zunächst alle  N Teilchen in dem einen Volumen A enthalten sind. Sobald ein zufällig ausgewähltes Teilchen auf die Öffnung trifft, wechselt es in den jeweils anderen Bereich über. Nach kurzer Zeit finden Wechsel von A nach B wie von B nach A statt. Der Platzwechsel ist nicht mit einer Energieänderung verbunden. (Im betrachteten Ein-Niveau-System hat es keinen Sinn, eine Temperatur zu definieren, weil T ja eine Aussage macht, wie angeregte Energie-Zustände das System besetzt werden.) Es gibt zwei Darstellungsmodi:

a) von jedem Teilchen (unterschieden durch unterschiedliche Orte) wird gekennzeichnet, in welchem Raum es sich befindet.

b) Die Teilchen in Raum A und die in Raum B werden gruppiert, wie in der Abbildung 3.

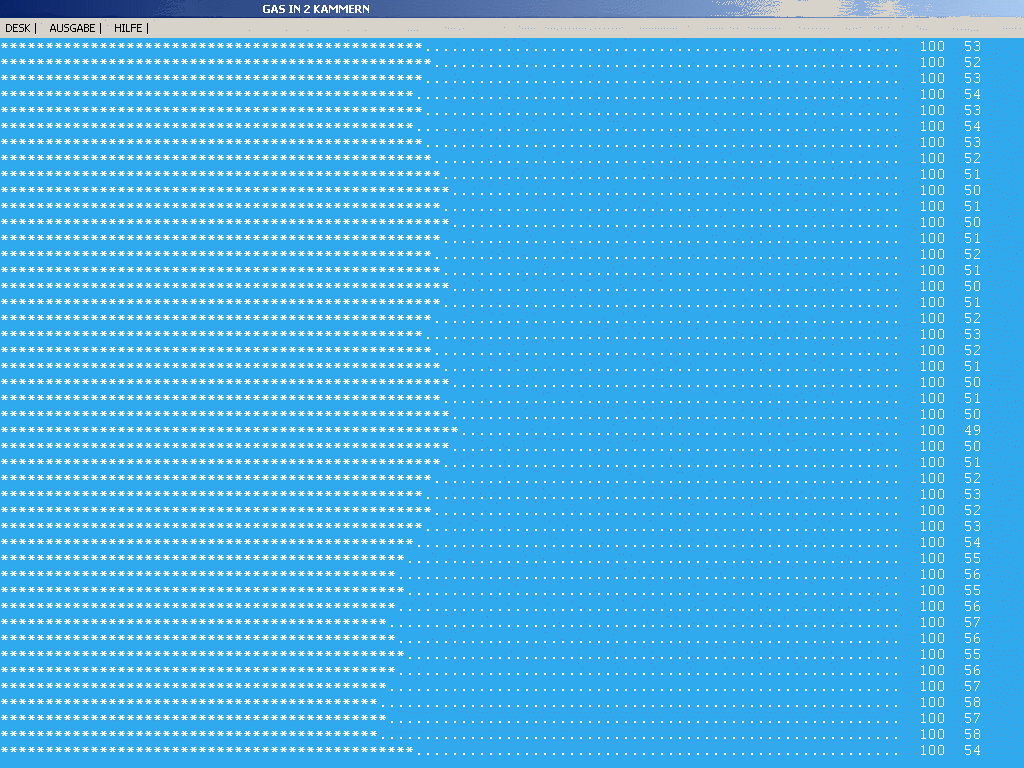Abb. 3: Diffusion eines Gases aus einem Raum A in einen Raum B. "*" kennzeichnet ein Teilchen in Raum A, ". " in Raum B (Darstellungsmodus b). Insgesamt werden hier 100 Teilchen eingesetzt, die Teilchenzahl in Raum A schwankt hier um 50. Die starken Fluktuationen mit Platzwechsel von jeweils einem Teilchen sind erkennbar.

Um N Teilchen aus N_max Teilchen für den Bereich A auszuwählen, gibt es g(N_max, N) Möglichkeiten, wobei

                             g(N_max,N) = N_max! / (N_max -  N)!·N!     mit N! = 1, 2, 3, .... N   ("N Fakultät")

Durch N! wird dividiert, weil es auf die N! Vertauschungen innerhalb der Teilchen von A nicht ankommt, ganz entsprechend durch (N_max -  N)! .

Zu einem durch das Wertepaar (N_max,N) charakterisierten Makrozustand gibt es g(N_max,N) mögliche Mikrozustände.

Als Entropie des Systems A wird definiert:  

(Vgl. Hinweis). Für festes N_max genügt sie einer Glockenkurve in Abhängigkeit von N. S, für die jeweilige Atomzahl N berechnet, ist in der oberen Zeile weiß dargestellt. Offenbar hat S ein Maximum für N = N_max / 2 .

In der unteren Zeile wird die durch häufige Wiederholung der Übertritte entstehende Häufigkeitsverteilung dargestellt, nämlich k_B · log (  h( N_max,N) ). Nach sehr großer Anzahl von Versuchen geht die Häufigkeitsverteilung in die Wahrscheinlichkeitsverteilung über (schwarz). Es stellt sich heraus, dass das Entropiemaximum mit der häufigsten Verteilung übereinstimmt.

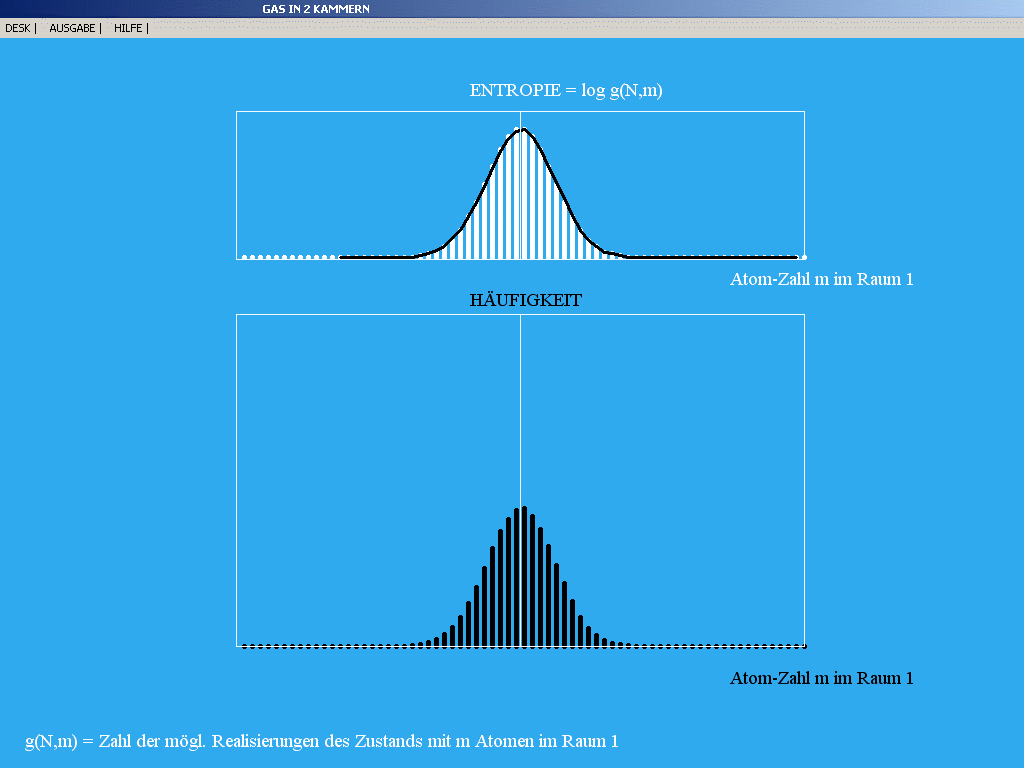Abb. 4: Vergleich von Häufigkeitsverteilung mit Wahrscheinlichkeitsverteilung (Entropie) bei sehr großer Zahl von Versuchen. In beiden Fällen ist der natürliche Logarithmus dargestellt. Das Maximum ist umso schärfer, je größer Nmax. Im Programm heißt Nmax: N und N: m.

Ergebnisse:

1. Es finden starke Fluktuationen der Teilchenzahlen N (bzw. m) statt.

2. Das Maximum der Entropie kennzeichnet die wahrscheinlichste Verteilung, die durch viele Versuche auch als häufigste Verteilung ermittelt wird.

3. Thermisches Gleichgewicht ist durch das Maximum der Entropie gekennzeichnet.

4. Die Entropie ist ein Maß für die Wahrscheinlichkeit einer bestimmten Verteilung mit N (bzw. m) Teilchen aus N_max  (bzw. N) Teilchen.

Beachten Sie wieder: All dies ist nur eine Folge der Statistik, also des geschickten Zählens bzw. des "Gesetzes der großen Zahlen", nicht von irgendwelchen "Mechanismen", die ein bestimmtes Verhalten der Teilchen "bewirken" würden. Der Gleichgewichtszustand ist der Zustand, zu dem die meisten Wege führen, der sich auf maximale Anzahl von Weisen realisieren lässt. Über die Teilchen selbst wurden fast keine Annahmen gemacht, außer dass für sie Ortswechsel möglich sind, und dass sie in einen Zustand mit der Energie E angeregt werden können.

Hinweis:

Es gibt mehrere gleichwertige Definitionen der Entropie. Statt g(N_max,N) kann zum Beispiel die Wahrscheinlichkeit p(N_max,N) für die entsprechende Verteilung verwendet werden. Alle Definitionen unterscheiden sich höchstens um einen belanglosen additiven Anteil, der für N => ∞¥ klein ist im Vergleich zu anderen Termen.

Anhang:

1. Nachweis, dass für große Teilchenzahlen die Formeln für T, S und 1/T = (∂S/∂U)_{N = konst}  miteinander konsistent sind , also die statische und die thermodynamische Definition

Aus S = k_B·log g(Nmax,N) soll mittels 1/T = (∂S/∂U)_{N = konst}   hergeleitet werden:      T  = E/k_B  1/ log [  ( N_max  - N )/N  ] , wobei

g(N_max,N) =   N_max! / (N_max - N)! N!                            (N aus N_max )

Zunächst:    S =  k_B  [   log N_max! - log (N_max - N)! - log N! ]

Wegen der für große N gültigen Näherungsformel nach Stirling              log N!   »   N·log N - N         gilt dann:

 S =  k_B  [   N_max log N_max - (N_max - N)  log (N_max - N) - N  log N   - N_max + (N_max - N)  + N ]                und damit

 S =  k_B  [   N_max log N_max - (N_max - N)  log (N_max - N) - N  log N     ]

 S = -  k_B [   (  (N_max - N) log ( (N_max - N) / N_max )    +  N  log N/N_max    ]

 S = -  k_B  [ N_max   (  (1 - N/N_max) log ( (1- N/N_max )    +  N/N_max  log N/N_max    ]

S ist damit proportional zu N_max (extensive Größe ! )  und hängt sonst nur mehr von den Teilchenzahl-Verhältnissen x = N/N_max ab, also:

 S = -  k_B  N_max  [ (  (1 - x) log ( (1- x )    + x  log x   ]

 Wenn jetzt definiert wird:  1/T = (∂S/∂U)_{Nmax = konst}  bzw. wegen U = N·E    

 1/T = 1/E (∂S/∂N)_{Nmax = konst}  = 1/E  (∂S/∂x)_{Nmax = konst} 1/N_max , dann folgt:

1/T = - 1/E k_B [ -(1- x) 1/(1-x) - log (1-x) + x 1/x + log x ] = - 1/E k_B [ - log (1-x) + log x  ] = 1/E k_B [ log (1-x)/x  )   bzw. eben

Man sieht, T ist im Unterschied zu S eine intensive Größe, die nur vom Teilchenzahl-Verhältnis x abhängt. Dieser Ausdruck wird für die Simulation des Programms ENTROPIE auch bei kleineren Teilchenzahlen als Näherungswert für T benutzt.

2. Nachweis, dass sich eine Nullpunktsverschiebung, z.B. im Zusammenhang mit der Grundzustandsenergie, nicht auswirkt. Diese sei jetzt E₀ =/= 0. Dann gilt z.B. für die mittlere (Anregungs-)Energie

<E> = ∑_i p(E_i )·E_i  

mit p(E_i) = exp ( - (E₀ + E_i ) / k_BT ) / Z               und            Z = ∑_i exp ( - (E₀ + E_i ) / k_BT ) .

In Zähler und Nenner lässt sich der Faktor exp ( - E₀/ k_BT ) ausklammern und wegkürzen. Sie erhalten wieder das frühere Ergebnis mit den (Anregungs-)Energien E_i. Analog für unser Modellsystem mit der (Anregungs-)Energie E:

N / N_max = exp ( + E₀/ k_BT ) / ( exp ( + E₀ / k_BT ) + exp ( + (E₀ + E ) / k_BT ) )

= exp ( - E) / k_BT ) / ( 1 + exp ( - E / k_BT ) ) wie oben.

Rückwärts folgt nach Auflösung nach T die gleiche Definitionsgleichung für T wie oben.

Zusammenfassung:

Für ein einfaches Modellsystem wurde die Definition der Begriffe Temperatur und Entropie theoretisch und experimentell mittels Simulationen untersucht. Daraus ergibt sich der vereinfachende Vorschlag, für die Schule die Temperatur in zwei Schritten zu definieren:

1. Die Temperatur T ist ein objektives Maß für den Wärmezustand eines Systems (im thermischen Gleichgewicht).

Der Wärmezustand kann an der Schule nicht exakt definiert werden, doch sollten einige wesentliche Aspekte, die im Text erläutert sind, zur Sprache kommen.

2. Die Temperatur T ist ein Parameter, der bestimmt, wie die Energien von Teilchen im thermischen Gleichgewicht verteilt sind. Je höher die Temperatur T, desto mehr Teilchen werden in höhere Energien angeregt, oder in desto höhere Energien werden Teilchen angeregt.

Das ist auch kompatibel mit üblichen Aussagen zum idealen Gas - die Anregungsenergie ist hier kinetische Energie - , aber eben auch zu anderen in der Schule behandelten Systemen, die keine kinetische Energie haben, wie die Strahlung. Insbesondere ist das kompatibel zu der Aussage, dass beim idealen Gas die mittlere kinetische Energie proportional zur absoluten Temperatur ist.

Ein derartiges Konzept könnte falsche Argumente, wie sie in Schulbüchern vielfach üblich sind, verhindern.

(zuletzt aktualisiert: Juli 2013)

(einige Formulierungen verschärft: Juni 2018)