Startseite FORPHYS Physik für Schülerinnen und Schüler Der FKG- Roboter FORPHYS- Mess- Interfaces Forschendes Lernen im Physik-UR Würzburger Quanten- physik- Konzept Grundfakten der Quanten- physik Materialien Physik-UR Physika- lische Analysen Experiment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2014

(Quantenauslöscher)

Anleitung:  Verwenden Sie den LCD-Bildschirm mit diesem Text als Lichtquelle. Führen Sie die Versuche mit einem Polarisationsfilter durch, z.B. der einen Hälfte einer Polarisationsbrille. Bezugsquelle z.B.  www.astromedia.de, Tel. 0201/6349760: Liefert u.a. Polarisationsbrille (Nr. 277.PBR, 2 Euro), Polarisationsfolie (Nr. 408.PDI, 7,90 Euro). Wenn Sie die Brille auseinander schneiden, stehen Ihnen zwei Polarisationsfilter zur Verfügung. Vorbereitung: Schauen Sie durch ein Polfilter auf den Bildschirm. Drehen sie es bis zur vollen Durchlässigkeit. Markieren Sie das Polfilter durch einen Pfeil, der die Polarisationsrichtung darstellen soll. Schreiben Sie AN dazu. Schauen Sie dann auch gleichzeitig durch die zweite Hälfte der Pol-Brille, drehen Sie diese bis zur vollen Durchlässigkeit und markieren Sie auch diese Richtung mit einem Pfeil. Schreiben Sie T dazu. Wenn beide Pfeile gleichgerichtet sind, sollte dann Licht durch beide hintereinander liegende Polfilter (weitgehend) ungeschwächt hindurchtreten. Hinweis: Es geht hier nicht darum einen "Quantencharakter" von Photonen zu "beweisen", sondern nur darum, beobachtetes Verhalten mit Quanteneigenschaften zu deuten. Dass eine andere Deutung möglich ist, ist hier belanglos.

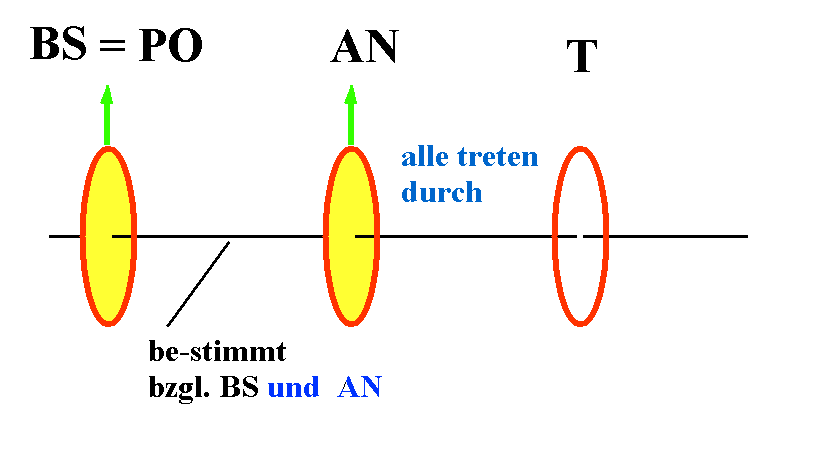
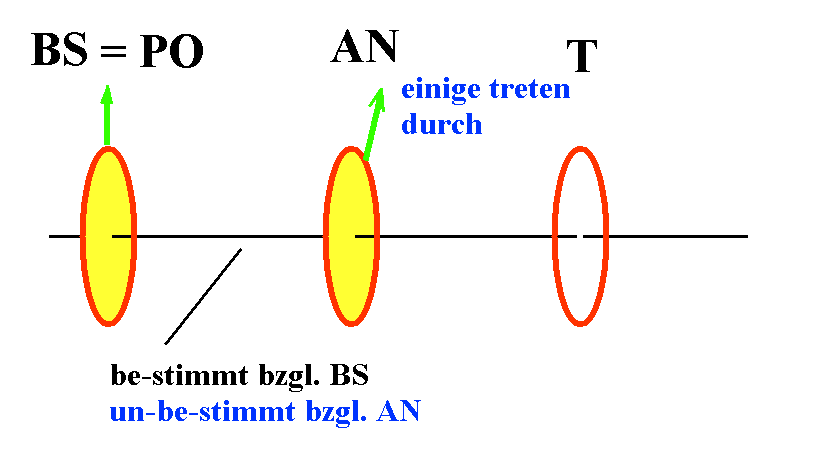
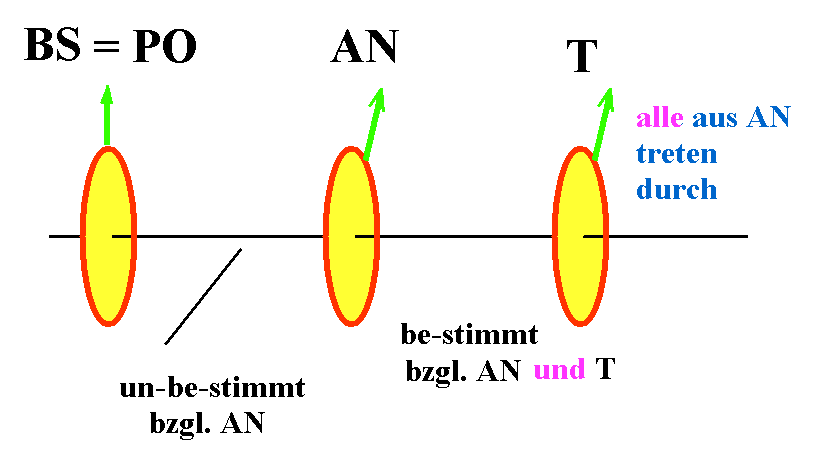
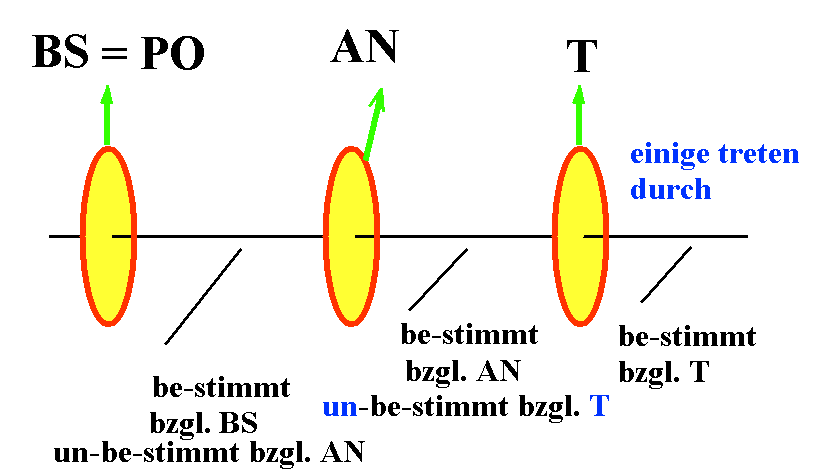
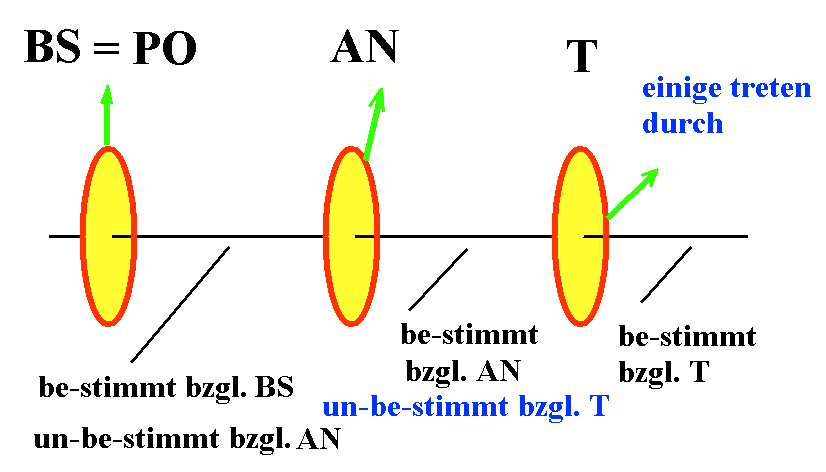
1. Versuch: Seit der "Vorbereitung" wissen Sie, dass vom LCD-Bildschirm BS polarisiertes Licht ausgeht wie von dem Polarisator PO der Zeichnung. Sie stellten das mit einem Polarisationsfilter (Analysator AN) fest, das sie unterschiedlich orientierten. a) Besitzt das Bildschirm-Licht eindeutige Polarisation? Das ist der Fall, wenn es eine Orientierung von AN gibt, bei der kein Licht passieren kann und eine dazu senkrechte, bei der AN  alles Licht von BS ("Bildschirm") passieren lässt. b) Identifizieren Sie die Polarisationsrichtung BS des Bildschirms. Wenn AN maximal viel Licht durchlässt, ist BS parallel zu AN, wenn AN kein Licht durchlässt, ist BS senkrecht zu AN polarisiert. Ein Polfilter stellt damit ein Messgerät dar für die Eigenschaft von Photonen "gemäß der Orientierung des Polarisators polarisiert". Eine solche Messung soll im Folgenden als Idealtyp einer Messung aufgefasst werden, an der Eigenschaften jeder idealen quantenphysikalischen Messung studiert werden. 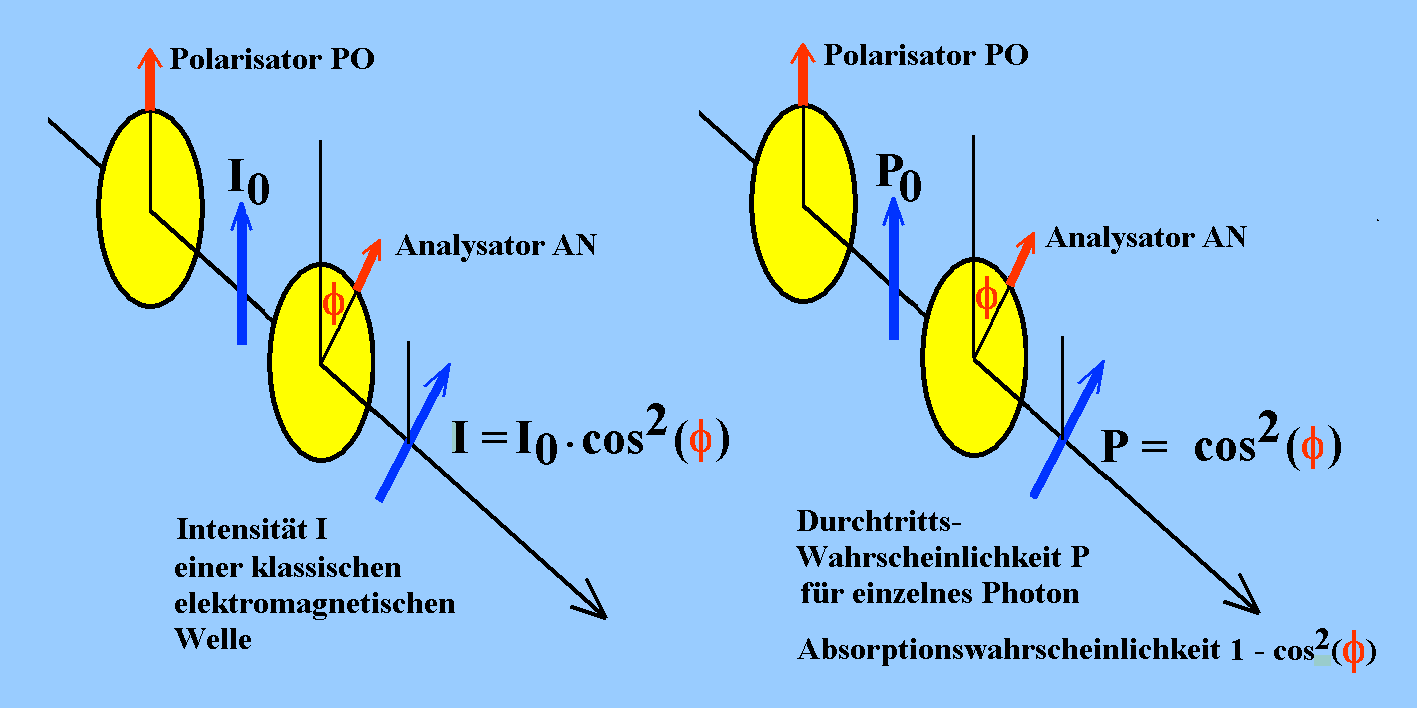Polarisiertes Licht lässt sich auch klassisch betrachten (diesen Schritt sollten Sie im ersten Durchgang überspringen): Nehmen Sie als Maß für die Intensität des durchgelassenen Lichts das Betragsquadrat der elektrischen Feldstärke E des durchgelassenen Lichts.  Zerlegen Sie den E-Vektor des einfallenden Lichts in die Komponente des durchgelassenen und des dazu senkrechten, also gesperrten Lichts. c) Bei welchem Winkel φ kann kein Licht passieren, bei welchem Winkel φ alles Licht, wenn polarisiertes Licht in den Analysator AN eintritt?

2. Versuch (Be-stimmtheit einer quantenphysikalischen Messgröße): Polarisiertes Lichts einer Richtung BS ("Bildschirm") lässt sich auch quantenphysikalisch betrachten als Strom von Photonen mit der Eigenschaft "polarisiert bzgl. der Richtung BS". Alle Photonen, die den Bildschirm verlassen, besitzen die Eigenschaft "polarisiert bzgl. der Richtung BS".  Diese Richtung haben Sie mit dem Polarisator AN gefunden. Gibt es unter den Photonen, die den Bildschirm BS verlassen, Photonen, die senkrecht zur Richtung BS, also auch senkrecht zu AN polarisiert sind? Entscheiden Sie durch das Experiment. Beide Messungen zeigen:    Photonen, die den Bildschirm verlassen, haben be-stimmte Polarisation bzgl. BS (und auf keinen Fall senkrecht dazu). Alle Photonen mit be-stimmter Polarisation bzgl. BS können durch einen parallel ausgerichteten Analysator AN hindurchtreten. Daran erkennen wir, dass die Photonen be-stimmte Polarisation bzgl. BS als Eigenschaft haben . (Wenn BS und AN gleich polarisiert, haben die Photonen dann auch schon vor AN auch be-stimmte Polarisation bzgl. AN.) Man spricht von einer "be-stimmten" Eigenschaft, wenn das Quantenobjekt diese Eigenschaft tatsächlich hat.  Im Gegensatz dazu: Eine Messgröße heißt in der Quantenphysik un-be-stimmt, wenn Messungen dieser Größe zwar jeweils einen eindeutigen Wert liefern , obwohl das Quantenobjekt diese Eigenschaft nicht hat. Mehrfache Messungen dieser Größe liefern dann i.A. unterschiedliche ("streuende") Werte, Indiz dafür, dass das Quantenobjekt diese Eigenschaft nicht hat. (Woran man sich gewöhnen muss ist, dass jede einzelne Messung dennoch ein klares Ergebnis liefert.) (Das gilt auch für den Vektor des elektrischen Felds entsprechend der klassischen Überlegung.) Bei schräggestelltem AN haben aus BS austretende Photonen vor AN bzgl. AN un-be-stimmte Polarisation, erkennbar daran, dass bei beliebiger Schrägstellung nicht alle Photonen AN passieren können. .

3. Versuch (Reproduzierbarkeit einer Messung): Wenn ein Photon durch einen Analysator mit der Richtung AN hindurchtritt, stellt dies eine Messung der Polarisation dar. Nach dem Durchtritt besitzt das Photon mit Sicherheit die Eigenschaft "polarisiert bzgl. einer Richtung AN". Das zeigen Sie, wenn Sie die Messung mit einem gleichgerichteten Polarisator T ("Tester") ein zweites Mal durchführen (gleiche Orientierung des Polarisators T wie der Analysator AN). Diese sollte diese unmittelbar danach das gleiche Ergebnis liefern. Weisen Sie das nach! Der Versuch lässt sich aber auch anders auffassen: Von einer vernünftigen Messung muss erwartet werden, dass sie reproduzierbar ist, d.h., wenn die Messung in gleicher Weise unmittelbar danach wiederholt wird, sollte sie das gleiche Ergebnis liefern. Genau das haben Sie gezeigt. Man sagt:    Auch quantenphysikalische Messungen sind reproduzierbar!   Sie stellen also verlässliche Messungen dar. Vergessen Sie aber nicht: Die Messung der gleichen Eigenschaft durch T bestätigt auch, dass die Photonen die Eigenschaft "polarisiert bzgl. einer Richtung AN" tatsächlich besitzen. Auch der Ort eines Quantenteilchens lässt sich zuverlässig messen. Gleiches gilt für die Geschwindigkeit eines Quantenteilchens. Im geschilderten Sinn sind Orts- und Geschwindigkeitsmessungen reproduzierbar.

4. Versuch (Objektive Un-be-stimmtheit): Sie wissen mittlerweile, dass von einem Bildschirm BS Photonen ausgehen mit der Eigenschaft "be-stimmte Polarisation bzgl. BS". Mit einem parallel ausgerichteten Polarisator T könnten Sie das bestätigen. Stellen Sie nun zwischen Bildschirm BS und einem parallel ausgerichteten Polarisator T einen Analysator AN mit "schräger Orientierung". Die AN passierenden Photonen haben dann "be-stimmte Polarisation bzgl. AN". . Wenn einige von ihnen auch T (parallel BS) passieren, entsteht ein Problem: Vom Bildschirm ausgehende Photonen haben be-stimmte Polarisation bzgl. BS (auf keinen Fall senkrecht dazu). Warum können dann einige von ihnen auch AN passieren? AN passierende Photonen haben be-stimmte Polarisation bzgl. AN (auf keinen Fall senkrecht dazu). Warum können dann einige von ihnen auch T passieren? T passierende Photonen haben wieder die be-stimmte Polarisation bzgl. T bzw. BS. Das wird so interpretiert: Photonen mit be-stimmter Polarisation bzgl. BS haben un-be-stimmte Polarisation bzgl. AN. Es ist also un-be-stimmt, ob ein den Bildschirm verlassendes Photon den Analysator AN passieren wird oder nicht. Führt man eine Messung bzgl. AN durch, so kann die Messung einige Photonen mit be-stimmter Polarisation bzgl. AN liefern (deren Wahrscheinlichkeit hängt mit der klassischen Überlegung von Versuch 1 zusammen). Solche Photonen sind zugleich un-be-stimmt bzgl. T und BS. Es ist also un-be-stimmt, ob ein AN verlassendes Photon den Analysator T passieren wird oder nicht. Eine Messung bzgl. T kann deshalb einige Photonen mit be-stimmter Polarisation bzgl. T bzw. BS liefern. Es ist nicht vorhersagbar, welche Photonen das sein werden. Ein Quantensystem, das bzgl. einer Eigenschaft (BS) be-stimmt ist, kann zugleich bzgl. einer anderen (komplementären) Eigenschaft (AN) un-be-stimmt sein.    Das gilt z.B. auch für Ort und Geschwindigkeit eines Teilchens. Wenn ein Quantenteilchen einen be-stimmten Ort hat, ist zugleich seine Geschwindigkeit un-be-stimmt. Für ein solches Teilchen findet man dann mit gewissen Wahrscheinlichkeiten beliebige Geschwindigkeiten.

5. Versuch (Komplementarität): Schritt a) Polfilter T so orientiert, dass kein Bildschirm-Licht mit Polarisation BS passieren kann: => T senkrecht zu BS orientiert; den Bildschirm BS verlassen Photonen mit be-stimmter Polarisation bzgl. BS. (Diese haben auch bzgl. T be-stimmte Polarisation, nämlich senkrecht dazu.) Kein parallel zu T polarisiertes Photon  wird beobachtet. Schritt b) Polfilter AN zwischen BS und T. Bei geeigneter "schräger" Orientierung von AN können einige Photonen auch T passieren: Diese haben vor dem Durchtritt durch T be-stimmte Polarisation bzgl. AN und un-be-stimmte bzgl. T (es ist un-be-stimmt, ob sie parallel oder senkrecht zu T polarisiert sind, ob sie T passieren werden oder nicht). Einige von ihnen können deshalb mit einer gewissen Wahrscheinlichkeit auch T passieren. Diese haben dann wieder be-stimmte Polarisation bzgl. T, diesmal parallel T. Ihre frühere Polarisation bzgl. BS (und senkrecht T) nach dem Austritt aus BS ist völlig vergessen worden. =>     Die Eigenschaften "be-stimmte Polarisation bzgl. (schrägem) AN" und "be-stimmte Polarisation bzgl. T" sind komplementär zueinander, d.h. kein Photon kann (zwischen AN und T) beide Eigenschaften zugleich besitzen. Das gilt jetzt auch für die Polarisationen bzgl. BS und T. Die Messung von T macht dann das Ergebnis von AN ungültig. Zuvor hatte die Messung von AN die Polarisation bzgl. BS ungültig gemacht. Allgemeiner:            Ein Quantenobjekt kann nicht alle klassisch denkbaren Eigenschaften gleichzeitig besitzen.        Ebensowenig kann ein Quantenteilchen zugleich Ort und Geschwindigkeit (Impuls) als Eigenschaften besitzen.    Es gibt viele weitere Paare von komplementären Messgrößen, also von Größen, die ein Quantensystem nicht zugleich als Eigenschaften besitzen kann.  Das ist eines der wichtigsten Grundfakten der Quantenphysik. Anders als in der klassischen Physik, wo alle Messwerte zu gleichzeitig existierenden Eigenschaften des Systems gehören, gibt es in der Quantenphysik Messgrößen, die nicht gleichzeitig Eigenschaften eines Quantensystems sein können, obwohl reale Messungen in jedem Fall eindeutige Messwerte liefern. Man sollte sich deshalb nicht wundern, dass man z.B. von einem Atom oder Elektron nicht gleichzeitig Ort und Geschwindigkeit angeben kann. Eine Messung liefert sicher einen be-stimmten Ort. Der Ort ist dann Eigenschaft des Quantenteilchens. Dann ist aber die Geschwindigkeit un-be-stimmt, d.h., diese ist nicht Eigenschaft des Quantenteilchens. Es ist un-be-stimmt, ob bei einer nachfolgenden Messung dieser oder jener Messwert für die Geschwindigkeit eintreten wird. Eine tatsächliche Messung der Geschwindigkeit liefert dann irgendeinen der möglichen, also einen eindeutigen, be-stimmten Wert für die Geschwindigkeit. Dann ist aber die vorherige Messung des Ortes ungültig geworden. Es ist unbestimmt geworden, ob nachfolgende Ortsmessungen diesen oder jenen von streuenden Messwerten liefern würden. Es gab in den vergangenen Jahrzehnten viel Erstaunen darüber, dass Ort und Geschwindigkeit nicht gleichzeitig be-stimmt sein können. Quantenteilchen sind eben anders als klassische Teilchen: Wenn wir zur Kenntnis nehmen, dass Ort und Geschwindigkeit wie andere komplementäre Größen (z.B. die Polarisationen bzgl. unterschiedlicher Richtungen) nicht gleichzeitig Eigenschaften eines Quantenteilchens sein können, können wir diese Tatsache eher akzeptieren.

6. Eine neue Auffassung des Versuchs zur Komplementarität:  Der Quanten-Radiergummi Zur Erinnerung: Versuch 5 lief so ab: Schritt a) Das Polfilter T war senkrecht zu BS orientiert. Kein Photon vom Bildschirm (mit der be-stimmten Polarisation BS) kann das Polfilter T passieren. Schritt b) Ein Polfilter AN  wird zwischen BS und T gestellt. Bei "schräger" Orientierung von AN können einige Photonen auch T passieren: Nach dem Durchtritt durch AN hatten sie be-stimmte Polarisation bzgl. AN, aber es war un-be-stimmt, ob sie parallel oder senkrecht zu T polarisiert sind, ob sie T passieren werden oder nicht). Einige von ihnen können deshalb mit einer gewissen Wahrscheinlichkeit auch T passieren. Sie hatten das so gedeutet:     Die Eigenschaften "be-stimmte Polarisation bzgl. AN" und "be-stimmte Polarisation bzgl. T" sind komplementär zueinander.   Das lässt sich auch anders auffassen: Vor dem Einstellen des Polarisators AN konnte kein Photon T passieren, weil es be-stimmte Polarisation bzgl. BS hatte. Durch AN wird die Eigenschaft "be-stimmte Polarisation bzgl. BS" ausgelöscht (ausradiert). Sie ist nach dem Durchtritt durch AN vollständig vergessen worden, weil die durchtretenden Photonen jetzt die Eigenschaft "be-stimmte Polarisation bzgl. AN" haben. Das ist das Grundprinzip eines Quantenradierers (Quantenauslöschers). Er löscht bereits be-stimmte Eigenschaften aus, macht Messwerte ungültig. Er beruht auf der Komplementarität. Quantenauslöscher können in anderem Zusammenhang zu merkwürdigen Erscheinungen führen. .

Bei den Experimenten mit den Polfiltern dieser Seite sind immer sehr viele Photonen beteiligt; deswegen kann kaum von Experimenten mit klassischem Licht unterschieden werden. Einzelne Photonen an Polfiltern können eher mit simulierten Experimenten studiert werden: z.B. mit dem  PC-Programm POLARIS . Klicken Sie dazu das Browser-Fenster klein und starten Sie POLARIS aus dem Verzeichnis/von der CD.nn

Download des Programmpakets PHOTONEN mit dem Programm POLARIS.  Download einer Zusammenfassung: Polexperiment

..

.